翼尖形状对小展弦比摆翼水动力性能的影响

张生浩，闫文辉，周军伟，梅 蕾，于 东

（1.哈尔滨工业大学（威海）海洋工程学院，山东 威海 264209；2.北方工业大学机械与材料工程学院，北京 100144）

0 引 言

谈及仿生推进，多数人会联想到那些掌握着神秘的游动机理，拥有超高的推进效率，能在水中来去自如的海洋生物。近年来，越来越多的科研工作者致力于揭开这层神秘机理的“面纱”，不断解析海洋生物游动中暗藏的物理规律，并逐步应用于工程实践中。其中，仿鱼类波状游动的推进器设计制造已成为研究热点之一，如仿金枪鱼月牙形尾鳍的机器人[1-2]、三关节仿鲨鱼机器人[3]、机电一体化摆动机器鱼[4]等。

鱼类综合利用水动力的机动方式给人们以灵感，人们在观察和归纳鱼类推进作用机理的同时，也在逐步摆脱对鱼类生物构造的局限性，涌现新的设计理念，摆翼推进器就是其中之一。Belibassakis等[5-6]研究了将摆动的水翼置于船体下方作为助推装置，通过与海浪耦合，利用船体的升沉运动产生附加推力，达到节能的目的。Mao[7]研究了摆翼作为海洋结构物主动式稳定鳍，通过调节摆动角度与摆动幅度来适应周围环境变化，能够较好地维持航行器低航速下的稳定性。此外，也有研究者将摆翼设计成能量收集装置，Kumar等[8]在摆翼前方设计了弹性板，使得摆翼可以在海浪中被动地发生摆动，达到能量收集的目的。

在摆翼的应用中，其运动模型一般是前进、转动以及周期性平动的多自由度耦合运动。为了得到更高的推进效率，Lin 等[9]研究了二维摆翼在纯纵摇、纯升沉以及耦合运动的水动力性能，发现纯升沉运动比纯纵摇摆动的摆翼速度更高，而耦合运动的摆翼效率更高。大多数研究中，摆翼的运动被认为符合正弦模型，Das 等[10]及刘焕兴等[11]研究了非正弦式摆动对摆翼水动力性能的影响，指出不同形状的运动波形会影响前进速度及效率，在水动力性能大幅降低的高斯特劳哈尔数工况，使用改进的非正弦摆动可以使尾流区的旋涡恢复反卡门涡街的形式，提高摆翼性能。为了建立摆翼性能与流场结构之间的关系，Andersen 等[12]采用数值与试验相结合的方法研究了摆翼后方的尾迹，用皂膜法获得了更加清晰的尾流场，更加深入研究了尾流场与推力及阻力的变化规律。苑宗敬等[13]用三维矩形及椭圆形水翼模仿鱼尾鳍的周期性摆动，研究其水动力性能，展示了不同展弦比水翼的尾涡结构，直观地看出三维效应对尾涡场的影响。Abbaspour 等[14]在研究振荡翼时，以独特的视角显示了三维水翼两边扭曲中间平坦的尾涡层结构形式，尾涡在水翼后方发展，形成“环环相扣”的三维涡街。与二维水翼不同，有限展长的三维水翼在前进的过程中会在每个翼尖处形成一个拖拽的旋涡，如同一个“小型龙卷风”，将对周围流场起强烈的速度诱导作用，在升力下降的同时产生诱导阻力[15]，而且翼梢还可能存在空化[16]。Birch等[17]研究指出，翼尖涡强度在翼梢后缘立即达到最大值，并在下游流场的两倍弦长距离范围内，强度几乎保持恒定。翼尖涡在尾流场与水翼非定常运动甩出的首缘涡相互作用，产生了更加复杂的尾流场[18]，这种相互作用将影响水翼性能。在摆翼推进器非定常运动中，翼尖涡将引起巨大的能量损耗，设法降低翼尖损失是工程实践中提高推进器水动力性能的重要途经之一。

前期研究发现，较大展弦比的摆翼推进效率接近理想二维摆翼，但随着展弦比的减小，效率明显降低。考虑到实际应用中的摆翼在结构上以小展弦比为主，以及参考飞机机翼设计中对翼尖的处理办法，本文以改变摆翼的翼尖形状来降低翼尖损失为出发点，对不同翼尖形状的小展弦比摆翼水动力性能进行研究。文中以NACA 0012 翼型为基础，生成了两组共6 种不同翼尖形状的水翼模型；而后，从网格拓扑结构和尺寸、求解时间步长、湍流模型及计算收敛特性四个方面对数值方法进行验证。最后，对不同翼尖形状的摆翼性能和流场特征进行对比分析。

1 水翼模型

本文采用平直水翼作为研究基准，由NACA 0012翼型沿展向等弦长拉伸得到。考虑到实际作为推进器的摆翼在结构上很难做到非常大的展长，本文针对展弦比AR=2的水翼进行分析，如图1（a）所示。考虑到平直水翼在端部存在直角，可能引起端面流动分离，因此设计了倒圆的端面形状，如图1（b）所示。Jung等［19］在研究带端板的三维翼时指出，端板能够改善尖端涡流的形成，减小诱导阻力，从而使总阻力减小。参考这种思路，本文在水翼两端设计了由两个不同尺寸扁椭球构造的端板，其中心位置在翼型最大厚度的弦长处，以水翼端面为椭球的赤道平面，前半个扁椭球在弦向的长半轴为0.034 m，后半个扁椭球在弦向的半轴长为0.074 m，二者的短轴为0.01 m，展向最大厚度为0.008 m（极半径为0.004 m）。水翼均以弦长c=0.1 m，展弦比AR=2的矩形水翼为参考，水翼外形及投影形状如图1所示。

图1 不同翼尖结构三维图及投影图Fig.1 3D and projection drawings of hydrofoil with different wing tip structures

在后面的研究中我们发现，翼尖倒圆和端板都没有很好地抑制翼尖损失，因而又仿照螺旋桨的桨叶，设计了三种展弦比AR=2 的不同翼尖收缩形式。其中，椭圆形水翼几何参数简单，便于重复验证；翼尖加宽的椭圆形用于分析翼尖收缩程度的影响；带后掠的翼尖形状是在加宽椭圆形的基础上仿照侧斜螺旋桨的一个尝试。三种翼尖收缩形式的水翼如图2所示。

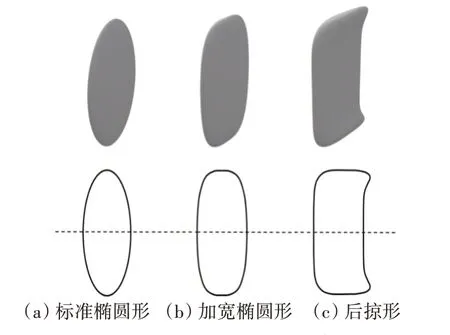
图2 不同翼尖收缩示意图Fig.2 Schematic diagram of hydrofoil with different wing tip contractions

2 运动描述

水翼运动分析采用绝对坐标系xoy，如图3 所示。水翼三自由度耦合运动分别为匀速前进、横荡、艏摇，其中横荡运动和艏摇运动方程分别为

其中旋转参考点为翼型导缘的顶点。

在前期研究中发现，较大摆幅比有利于提高效率[20]，但由于过大的摆幅不易实现，本文折衷选择摆幅比Y0/c=2.5，即横荡摆幅为Y0=0.25 m，运动频率初步选用f=1 Hz。考虑到水翼运动的最大摆角θ0将影响翼尖流动分离，本文对0.3 rad、0.5 rad及0.7 rad进行了对照研究，横荡与艏摇运动相位差为φ=π/2。一周期内水翼运动、受力情况如图3所示。

图3 水翼运动和受力情况示意图Fig.3 Schematic diagram of foil motion and force

3 性能参数

对比螺旋桨的进速系数定义，本文选用横荡摆幅B作为特征长度，定义进程hP=TVx与横荡摆幅B的比值为进速系数，以J表示

式中，进程与横荡摆幅如图3所示，T为摆动周期，Vx为前进速度。由上式可知，在摆动频率f和横荡摆幅B一定的条件下，改变进速Vx值即可得到不同的J。本文水翼运动的不同工况是指不同进速系数的工况。许多文献中，采用St数代替进速系数来描述摆翼的不同工况，两者关系表示为

定义绝对坐标系下，摆翼稳定工作后一个周期内沿前进方向力的积分均值为平均推力Fˉx，表示为

参照螺旋桨性能参数的定义，以水翼扫掠面积BH为参考面积，即横荡摆幅B与水翼展长H所围面积，以fB为参考速度，定义推力系数KT，表示为

按相对速度计算，摆翼推进器的工作雷诺数Re可表示为

式中，ν为运动粘度系数。本文各工况雷诺数Re在1.6 × 105～5.0 × 105范围内。

定义摆翼稳定工作后一个周期上横荡运动与艏摇运动瞬时功率的积分均值为平均输入功率，表示为

则推进效率可表示为

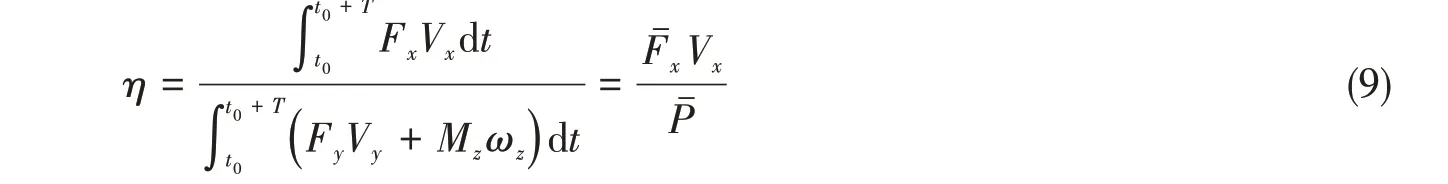
同时，与推力类似，将侧向力Fy和摆翼所受转矩Mz无量纲化为

式中，c为水翼弦长。

4 数值方法

4.1 控制方程

本文采用弹性变形网格以适应摆翼的多自由度耦合运动的模拟要求，其采用的连续方程和动量方程分别为

式中，Ω为控制体体积，A→为控制面，V→为流场速度，Vi为V→的分量，V→d为控制体表面运动速度，τij为黏性应力张量分量，p为压强。

本文采用FINE/Marine 不可压粘流求解器实现上述方程的求解。由于摆翼工作中伴随着明显的分离流，文中对比了常见的Menter[21-22]的k-ω模型和基于SST 模型的DES 模型[23]。其中k-ω模型是工程中应用最为广泛的两方程涡粘性模型之一，该模型主要求解湍动能k及其比耗散率ω的对流输运方程，对附着边界层湍流及适度分离湍流都有着较高的精度。DES模型在1997年由Spalart[24]提出，属于RANS/LES耦合算法之一，在分离流动的情况下预测准确性良好。

4.2 网格划分及边界条件

本文使用NUMECA/HEXPRESS 生成计算网格，仿真模型计算域是一个4 m×2 m×1 m的长方体，图4为计算域的三个加密区域，其网格尺寸如表1所示。

图4 计算域加密区域示意图Fig.4 Schematic diagram of calculation domain refinement area

表1 网格划分情况Tab.1 Details of mesh refinement

翼型表面网格单元大小参考Nordanger K[25]和魏良[26]的工作，初步选定为7 次细分，即翼型表面的网格长度为c/27。由于水翼运动关于xoy面对称，因此使用半模计算。

计算中采用的全六面体非结构网格，能精确捕捉物体的外形，而且计算域绝大部分网格单元都接近于长方体，网格的正交性十分优异，翼型表面及其周围的网格分布如图5所示。

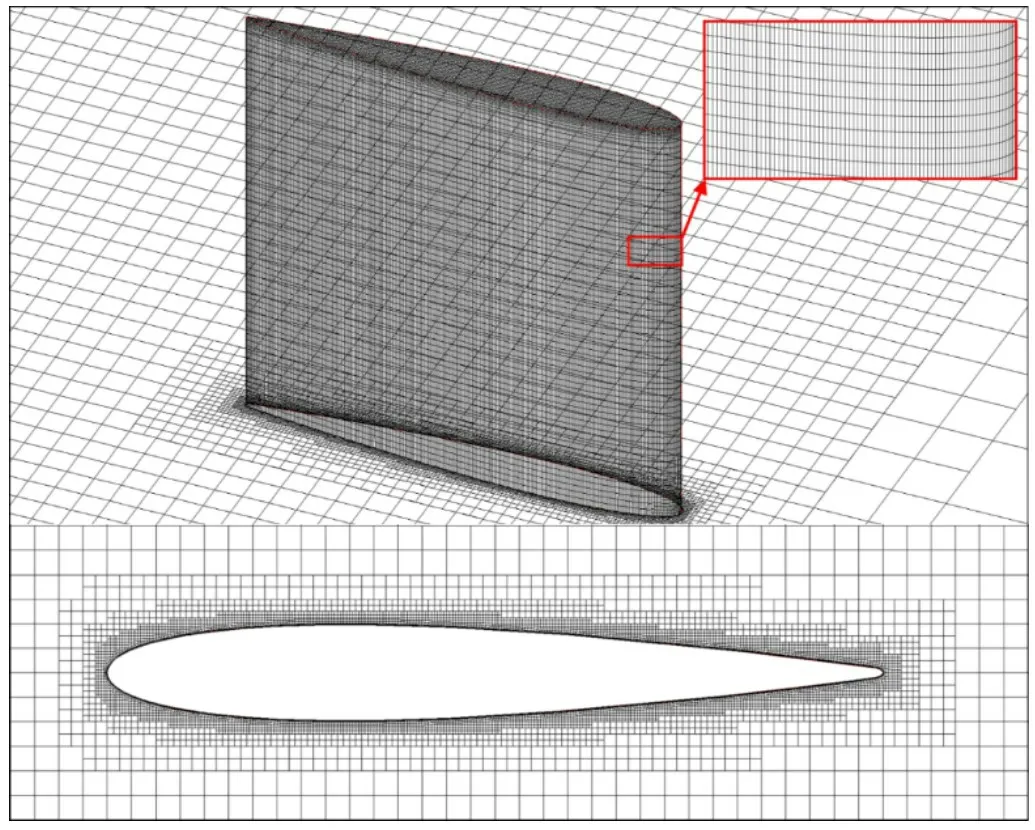
图5 水翼表面及周围网格分布示意图Fig.5 Grid distribution of foil surface and surrounding area

水翼壁面为无滑移壁面条件，水翼前方边界为远场，左、右侧及后方边界均为零压梯度，上方为描述压力，下方边界为镜像边界，如图6所示。

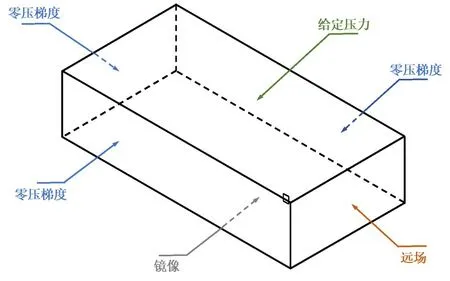
图6 边界条件Fig.6 Boundary conditions

4.3 数值可靠性验证

为验证NUMECA 软件数值模拟摆翼运动的可靠性，本文验证了Read[27]和Schouveiler[28]实验结果，同样采用NACA 0012翼型，升沉幅度比为0.75，旋转参考点在距离翼型前缘1/3弦长处，选取最大攻角为20°与25°的两种工况对比，如图7所示。

图7 数值验证Fig.7 Results of numerical verification

由图可知，软件求解结果与Read[27]和Schouveiler[28]的工作较吻合，本文所研究的水翼攻角与验证攻角相近，由此来看，数值方法对摆翼性能的计算结果较为可靠。

4.4 网格无关性验证

为了保证网格质量不会对计算结果产生影响，本文进行了大量的验证。这里列出其中比较关键的、以及较为有意义的一些影响因素的结果。

第一轮验证中，为研究沿弦向分布的水翼壁面最大网格大小对计算结果的影响，本文以弦长c为基准，通过改变水翼壁面的弦向网格大小，设计了四种网格细化方案，如表2 所示，验证工作的艏摇摆角均取为0.3 rad，湍流模型选用k-ω模型，时间步长为0.002 s。

表2 弦向网格细化方案Tab.2 Scheme of mesh refinement

计算结果如图8 所示，壁面网格大小对计算结果有较为明显的影响。方案1 的网格在一些分离较大的工况得到的结果曲线明显向右下方发生了偏移，峰值偏小。方案2 的网格求解结果较更细密网格的曲线有较小的偏差，部分工况数值仍然偏小。细分程度更高的方案3及方案4的网格求解结果趋于重合，可见，方案3的网格已经能满足网格无关性要求。

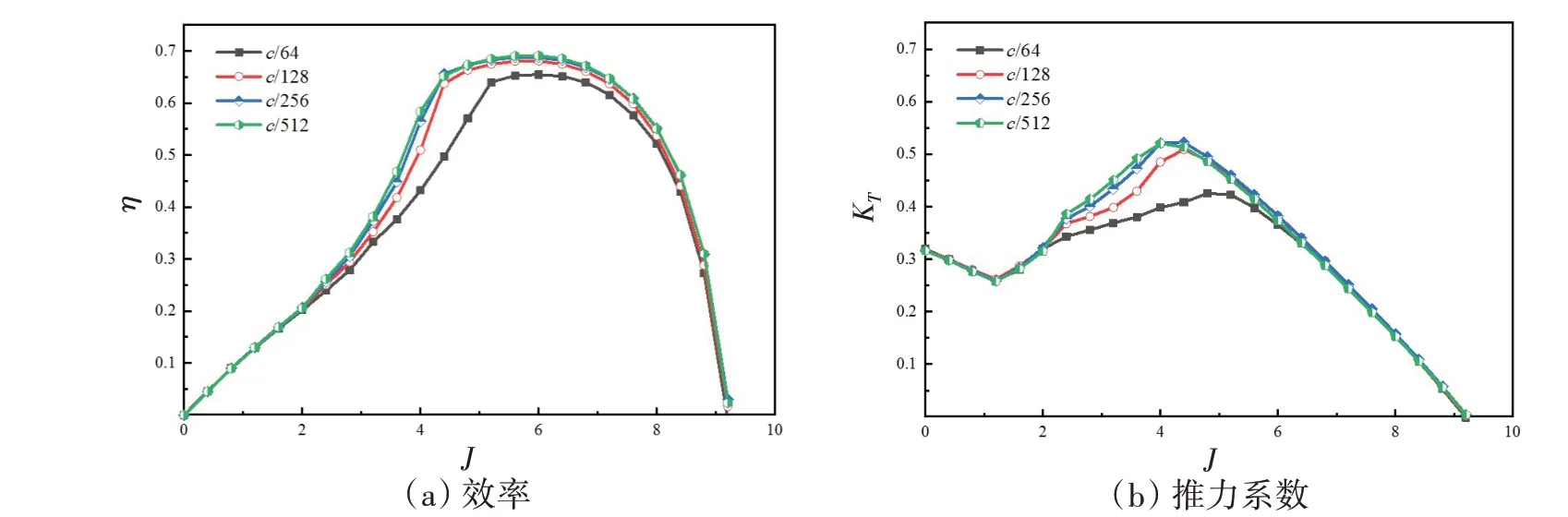
图8 不同壁面网格大小的结果性征曲线Fig.8 Performance curves under different wall mesh sizes

本文分析了壁面网格长度引起性能差异的原因。图9为不同壁面网格长度算例的首尾端网格节点分布，显然，随着壁面网格数量增加，翼型细节逐渐能够被准确捕捉。

图9 首尾端壁面网格分布示意图Fig.9 Schematic diagram of wall grid distribution at leading edge and trailing edge

图10还列出了四种网格长度在J=4时的流场，这是水翼攻角较大的一个工况，所选取的时间为尾涡充分发展后的某个整周期时刻。从图10（a）可以看出，采用方案1 的算例中，首缘已经出现明显的分离涡，而细化程度较高的算例结果中，尾涡依然附着在水翼表面，根据机翼的工作特点，可以推测，这是导致效率与推力系数下降的主要原因。

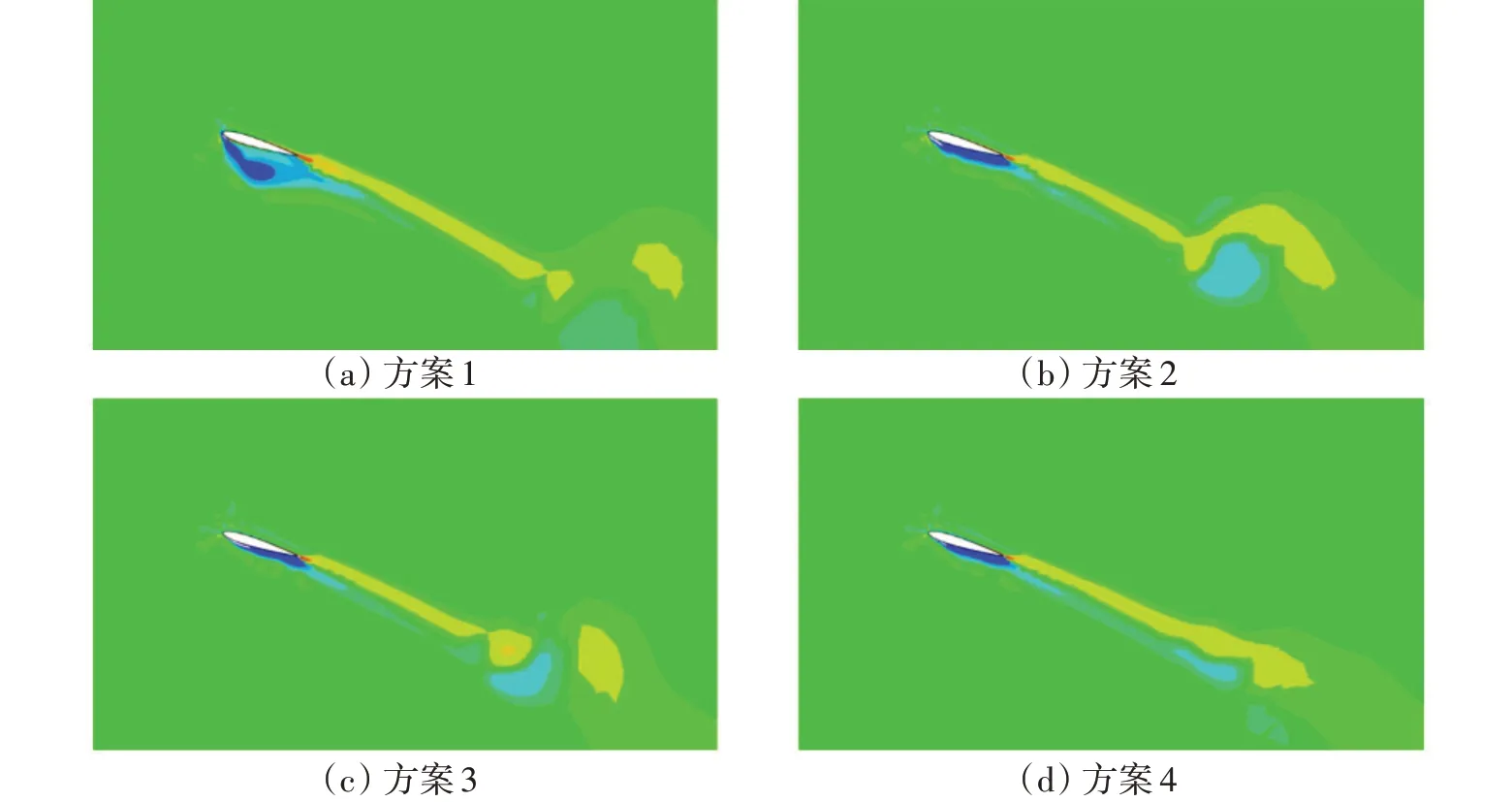
图10 J=4工况下某整周期时刻不同网格算例的尾流场Fig.10 Wake of different grid simulations at the whole period under J=4 condition

在第二轮验证中，考虑到水翼周围网格的加密程度会影响尾涡的分辨率，进而可能影响其性能。本文以细化方案3 的网格为基础，在加密区域II 和III（见图4），以及翼型附近的区域设计了进一步加密的方案（见图11），组合得到5种加密方案，如表3所示。

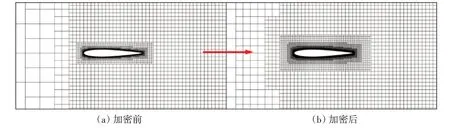
图11 翼型周围网格加密示意图Fig.11 Mesh refinement around foil

表3 尾流区域网格划分情况Tab.3 Details of mesh generation in wake region

计算结果如图12所示，无论怎样改变水翼尾流区域的网格大小，求解得到的性能曲线基本重合。相对来讲，对水翼周围网格加密后，性能得到了微幅提升，特别是较高进速系数工况的效率，提高了约1%～2%。但是整体来看，加密水翼周围网格，计算结果并没有出现大幅度改变。因此，从节省计算机资源的角度考虑，水翼周围网格大小重要性低于壁面网格大小，可在资源充沛时适当加密。可见，在研究水翼性能过程中，尾流区域的网格大小并不是重点考虑的因素，但尾涡脱落后流场发展的模拟仍需要足够的网格精度，要研究尾涡发展后的形态时，尾流区域有必要加密。

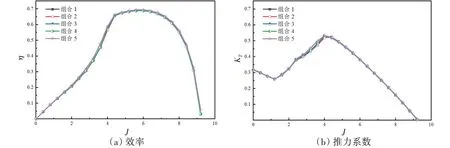
图12 翼型周围网格加密算例的效率及推力系数曲线Fig.12 Performance curves of simulations in wake region with different mesh sizes

通过本节研究发现，研究水翼性能时，必须确保水翼壁面网格满足网格无关性要求，而尾流区域的网格则可以适当调整，以控制网格总数，加快求解速度。后文中将选用方案3 和组合1 的网格进行分析。

5 结果与分析

5.1 湍流模型及时间步长的影响分析

由于非定常运动的水翼存在大量分离涡，不同湍流模型很可能使得分离涡状态不同，进而引起水翼性能求解差异，本文对比研究了k-ω（SST）以及DES两种常见的分离涡仿真湍流模型的结果。

图13 为不同湍流模型求解的性能曲线，整体来看湍流模型的影响较小，两种湍流模型得到的曲线基本相同。但在分离较大（进速系数较小）的工况下，性能出现了微幅差异，湍流模型有略微影响，而在高效运行工况，两种湍流模型得到的结果基本一致。

图13 不同湍流模型算例的效率及推力系数曲线Fig.13 Performance curves of different turbulence models

在较高进速系数工况，水翼工作攻角总小于失速角，尾涡呈现为“彗星式拖尾”状，分离较小，湍流模型影响较小。本文选取了分离较大工况下不同时刻的水翼尾涡场进行对比。图14 为J=4.4 时，水翼在T/8、T/4、T时刻的涡量场。对比图14（a）发现，两种湍流模型求解得到的水翼跨中分离涡形状不同，而翼尖涡形状差异很小，k-ω模型中，旋涡在壁面附近较为完整，随即在后方变得断断续续。而DES 模型在水翼跨中后方产生了多个小涡环，水翼壁面的旋涡也更为复杂。对比图14（b）发现，k-ω模型得到的首缘涡为单个脱落涡，而DES模型得到的脱落涡由多个较小的旋涡组成，这种多旋涡脱落将引起水翼压力发生波动，由此推测，这很可能就是与k-ω模型求解结果出现差异的原因。不过，在水翼性能研究中，湍流模型有一定影响，但并没有引起剧烈的性能变化，差异在可接受范围内，因而在随后性能研究中，本文初步选用k-ω模型。

图14 J=4.4时不同时刻水翼的尾涡场Fig.14 Wake with massive separation at different times

而后，本文研究了求解器时间步长对结果的影响，设计了时间步长为0.01 s、0.005 s、0.002 s、0.001 s 的算例进行对照。图15 为不同时间步长的计算结果，时间步长对各工况性能均存在较大影响，其中，较大的时间步长（如0.01 s与0.005 s）在非定常求解过程中存在较大加速度的时刻，造成数值解偏离真解，使得性能曲线形状发生改变，特别是图15（b）中，部分工况区间的推力系数曲线呈现明显凹凸性不一致的情况。虽然0.005 s 时求解得到的效率曲线已经基本趋于收敛，但推力系数曲线仍不能呈现正确的凹凸走势，时间步长需进一步减小。时间步长达到足够小（如0.002 s与0.001 s），算例性能曲线基本稳定，结果向真解收敛，本文选取0.002 s的时间步长，已能够满足求解精度。

图15 不同时间步长算例的性征曲线Fig.15 Performance curves of simulations with different time steps

水翼性能与涡分离状态息息相关，为了研究时间步长对首缘涡分离的影响，本文选取了性能差距较大工况下的尾涡场进行研究。图16 为J=3.6 时不同时间步长的算例在整周期时刻的尾流场，对比发现，时间步更小的算例，首缘涡更早发生分离，而较大时间步长对首缘涡分离较为迟钝。图16（a）中首缘涡仍附着在翼型表面，与其他结果对比，该时刻的首缘涡原本应当已经分离，而较大时间步长使得分离滞后，造成水翼两侧仍存在较大压力差，表现为该时刻仍然保持了较高的推力系数，因而推测这也是图15（b）中推力系数曲线发生明显凹凸不一致的原因。随着时间步长减小，旋涡分离差异越来越小，时间步长为0.002 s与0.001 s的流场基本相似，本文合理地选用时间步长0.002 s。

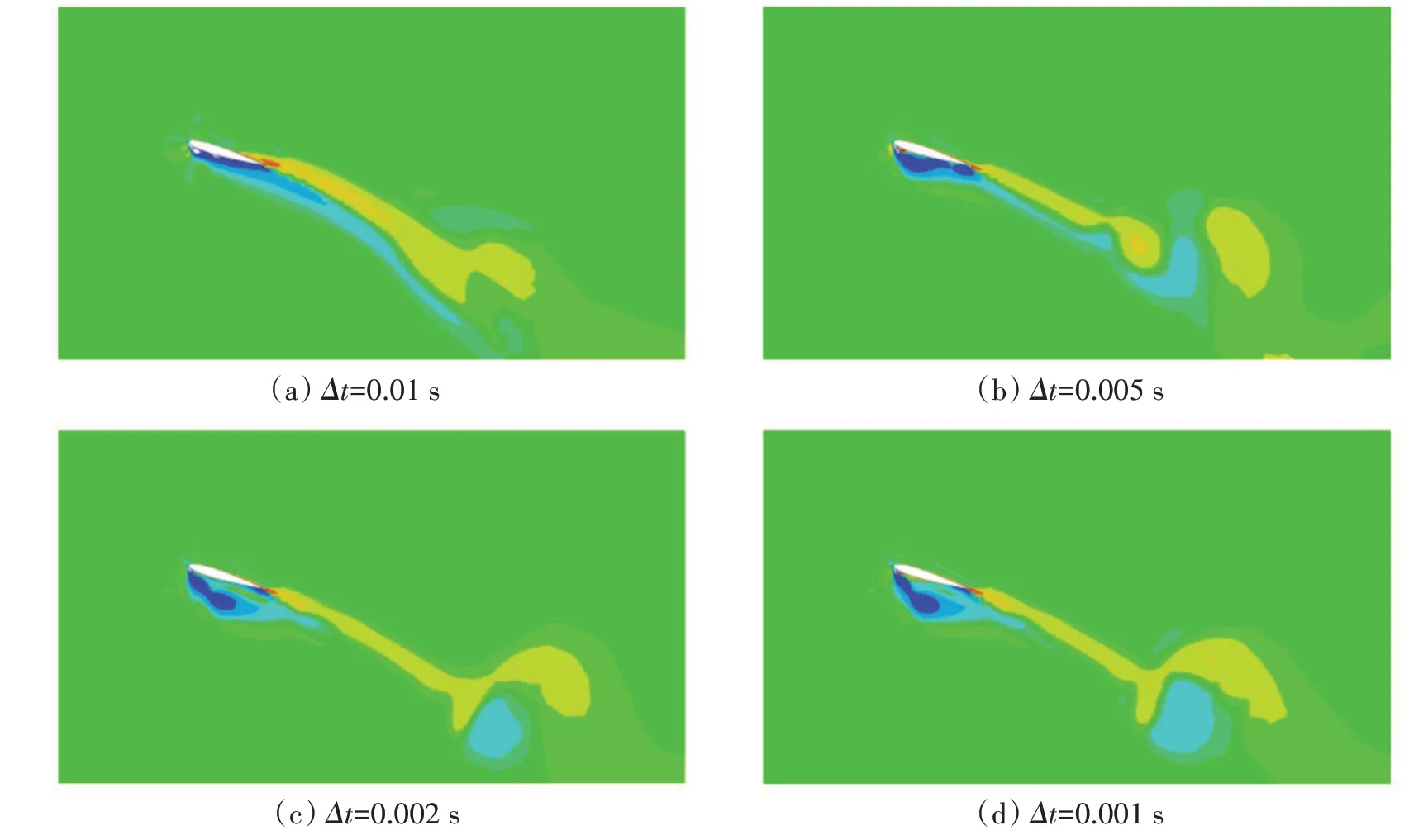
图16 J=3.6工况不同时间步长的尾流场Fig.16 Wake field with different time steps under J=3.6 condition

以下分析中，本文将选用k-ω模型，时间步长选用0.002 s。

5.2 性能的收敛性分析

为监控求解的性能曲线是否达到收敛，本文定义某时刻的均值效率η0为该时刻在一个周期时窗上的积分均值，表达式为

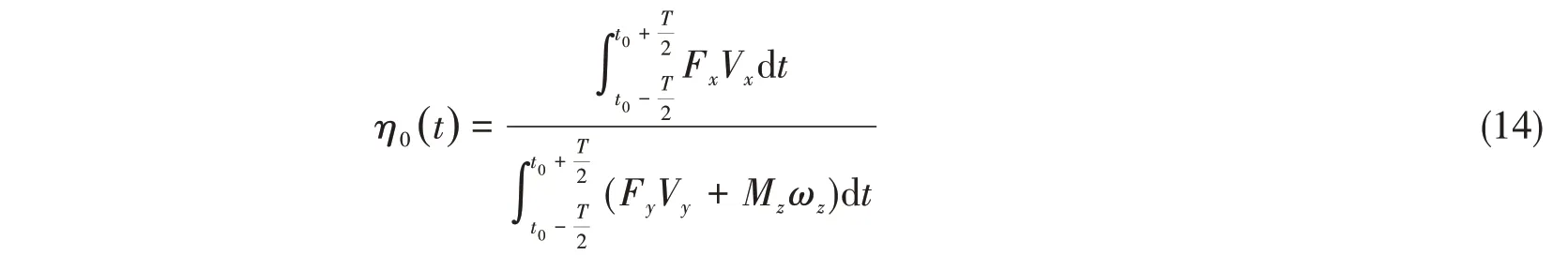
某时刻均值推力系数KT0的表达式与之类似，为

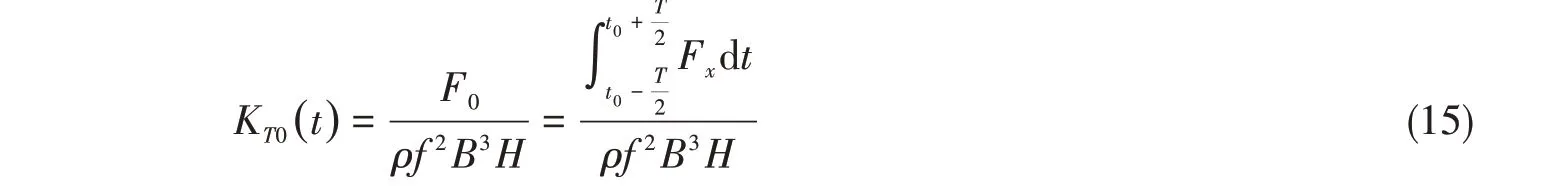
根据式（13）及式（14）对求解器产生的瞬时数据进行处理，得到不同工况下的性能收敛性曲线，如图17所示，对比发现，J较小的工况下推力系数收敛较慢，但求解过程总能在两个运动周期后达到稳定。可见，水翼性能研究至少需要求解2个以上运动周期，在舍去前两个周期数据的基础上，进行性能分析。

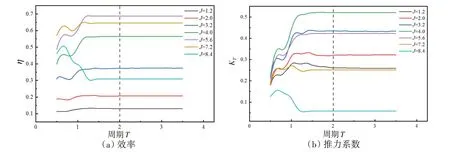
图17 性能收敛特性曲线Fig.17 Convergence characteristic curve of performance

5.3 端部影响

根据前文多次计算结果，对本文设计的三种翼尖结构的水翼进行求解。图18为不同翼尖结构的水翼性能曲线计算结果，图18（a）显示，改变翼尖结构并没有对效率产生明显的提高，三种结构在各工况效率差距很小。不过，进速系数越高的工况，倒圆及端板翼尖呈现出越来越高的效率优势，比平直翼尖高约1%～3%。图18（b）显示，端板在启动阶段推力系数微幅下降，但在高效运行的工况区间推力系数又微高于倒圆和平面翼尖的水翼，本文所研究的三种翼尖结构并没有像预期那样大幅改善推进性能。综合比较发现，虽然倒圆翼尖的水翼推力系数略微降低，但综合性能良好，一方面，倒圆水翼在进速系数较高时仍能保持较高的推进效率；另一方面，倒圆水翼结构复杂度比端板水翼小，更容易设计制造。因此，选用倒圆翼尖为佳。

图18 不同端部的水翼性征曲线Fig.18 Performance curves of different wing tip shapes

图19 是三种水翼峰值效率工况（J=6）侧向力及艏摇力矩系数时历曲线。对比发现，三种水翼驱动力在运动的半周期位置差异最大，此时水翼横荡速度及工作攻角均在峰值附近，翼尖形状对分离的影响最为明显。倒圆水翼的侧向力及艏摇力矩均处于较低水平。输入功率的主要贡献来自于侧向力，端板水翼所需驱动力最大，虽然端板降低了翼尖损失，但其驱动力随之增加，性能提升效果不如倒圆水翼。

图19 不同端部的水翼峰值效率工况侧向力及艏摇力矩系数时历曲线Fig.19 Time history of lateral force and yaw moment coefficient of foil with different ends under peak efficiency condition

为了研究不同翼尖形式对水翼表面压力分布的影响，本文选取了最高效率点工况的水翼。图20为J=6.0、t=4 s 时刻的跨中翼面压力分布曲线，对比看出，翼尖结构能够改变翼面压力分布，平直翼尖与倒圆翼尖正负压翼面分布大致相同，因此推力及效率十分相近。不同的是，端板水翼正压面的分布曲线更为尖锐，正压力有所减小，而负压面分布与其他两种翼尖基本相同。由此推测，这种正压翼面压力微弱减小是推力系数较另外两种结构略微增大的主要原因。

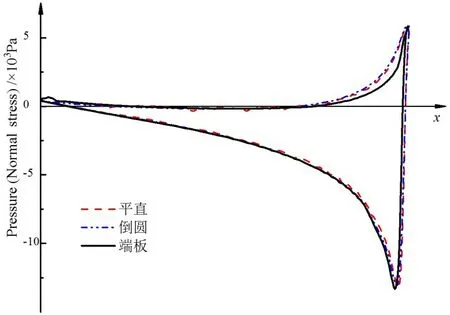
图20 不同翼尖结构的翼面压力分布曲线Fig.20 Pressure curves of different wing tip structures

考虑到攻角对端壁绕流流动可能具有较大的影响，本文选用综合性能较优的倒圆水翼做进一步研究，分别计算了0.5 rad、0.7 rad的工况，并与0.3 rad工况进行对照，得到的性征曲线如图21所示。

图21 不同摆角的水翼敞水性征曲线Fig.21 Performance curves of foil with different yaw angles

图21（a）显示，倒圆翼尖水翼还可以通过改变摆角的方式进一步提高效率，但是摆角增大后，导致摆翼推进器高效工作的区间减小。仅从峰值效率来看，摆角为0.5 rad的效率最高，高效工作的工况区间为J=3～5。此外，图21（b）显示，摆角越大，启动状态的推力系数越大，但在最高效率点附近的推力系数减小。因此，这提供了一种推进器启动过程的设计思路，即变摆角启动，以较大摆角启动，可在较低进速系数的工况达到高效状态，然后随速度增加逐渐减小摆角。

本文推测摆角不同的水翼峰值效率出现差异的原因可能是由翼尖涡强度不同引起的。图22 是不同摆角的倒圆水翼在峰值效率点工况不同时刻的尾涡场。对比同时刻在水翼对称切面内的尾涡强度可以发现，摆角越大，水翼产生的翼尖涡强度越低。由图21 可知，摆角越大，最高效率点工况的进速系数越低，意味着机翼来流速度降低很可能是翼尖涡强度减小的主要原因，由于翼尖涡能量损失减小，最高效率有所提高。当进一步增大摆角，虽然翼尖涡强度降低，但水翼各工况旋涡分离程度较大，流动的不稳定性对翼型水动力特性产生较大影响，最高效率反而降低。

图22 不同摆角水翼的尾涡场Fig.22 Wake field of foil with different yaw angles

为了提供摆翼推进器设计中所需要的数据，这里还列举了不同摆角下的最大侧向力系数和最大艏摇力矩系数曲线，如图23所示。

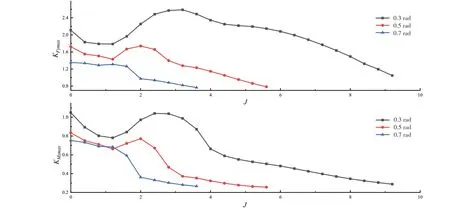
图23 不同摆角水翼在各工况下的最大侧向力及最大艏摇力矩系数曲线Fig.23 Maximum lateral force and maximum yaw moment coefficient of foil with different yaw angles

5.4 翼尖收缩形式的影响

最后，本文对四种翼尖收缩形式的水翼性能进行了研究，设置摆角为0.5 rad，得到的结果如图24所示。

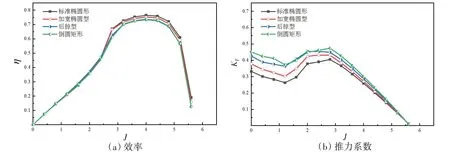
图24 不同翼尖收缩的水翼敞水性征曲线Fig.24 Performance curves of foils with different wing tip contractions

可以看出，标准椭圆形收缩的翼尖再一次提高了效率，图24（a）中标准椭圆形水翼的峰值效率达到了76.5%，相比矩形水翼在相同工况提高了约2.8%，加宽椭圆形水翼在高效工况区间效率略低于标准椭圆，后掠形水翼推进性能与矩形水翼相当。图24（b）显示，后掠形的水翼有较高的推力系数，但是两种椭圆水翼推力系数损失较明显，特别是起动阶段，矩形水翼较其他形状反而有较大的推力系数。总之，翼尖收缩接近椭圆，效率将提高，但相同展长下的投影面积减小，会损失推力，工程中可通过调整水翼尺度来达到指定推力。

本文推测水翼运行中椭圆形收缩的水翼输入功率较小、效率较高的原因可能是翼尖涡强度有所降低。图25为不同翼尖收缩形式水翼处于峰值效率工况（J=4.0）工作时，T、T/8及T/4时刻的尾涡切片图，对比证实了以上猜测。图中显示，各个时刻椭圆形、加宽椭圆形及后掠形收缩的翼尖涡强度依次增大。标准椭圆形收缩的翼尖有最低水平的翼尖涡强度，诱导阻力减小，翼尖涡损耗减小，因而效率提高。从图25（b）可看出，加宽椭圆水翼的翼尖涡强度略微增大，因此效率略低于标准椭圆水翼。后掠形收缩方式与矩形倒圆水翼的翼尖涡强度相当，因而性能曲线与倒圆水翼几乎重合。翼尖涡损耗是三维水翼不可避免的问题，通过改变翼尖收缩形式，可以有效降低翼尖涡强度。总体来看，翼尖按椭圆形收缩的翼尖形状最好，翼尖收缩越快，翼尖涡强度越大，效率越低。图26显示了标准椭圆、加宽椭圆及后掠形水翼的最大侧向力及艏摇力矩系数曲线。

图25 不同翼尖收缩形式的水翼尾涡切片图Fig.25 Wake vortices of hydrofoils with different wing tip contractions

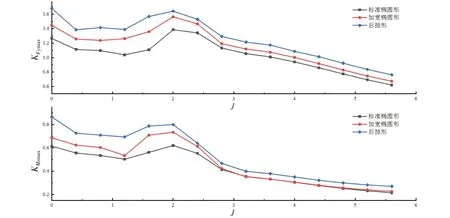
图26 不同收缩形式的水翼最大侧向力及最大艏摇力矩系数曲线Fig.26 Maximum lateral force and maximum yaw moment coefficient of foil with different wing tip contractions

6 结 论

本文详细验证了摆翼的水动力性能数值模拟方法，分析了6 种不同翼尖形状小展弦比摆翼（AR=2）的水动力性能，并探讨了引起性能差异的原因。经过大量数值计算及分析，得到以下结论：

（1）水翼表面弦向网格大小对数值结果有显著影响，当弦向网格长度小于c/256时，与更精密的网格求解结果基本相同。而在尾流场区域，网格尺寸对性能求解结果的影响较小。

（2）由于摆翼运动中的流场是明显的非定常过程，求解时间步长会显著影响水翼的水动力性能求解结果。此外，从计算收敛性来看，至少需要求解2 个周期以上的流场，求解得到的各项性能参数才能稳定。

（3）不同翼尖结构能够改变水翼表面的压力分布，但对水翼性能改善未能到达预期，后掠形摆翼也未能提高性能；椭圆形翼尖明显提高了推进效率，但推力系数有所降低。倒圆形翼尖处于居中水平，效率较高，推力系数也较大。

（4）存在最优的艏摇摆角，以实现最高效率。低进速系数情况下，选择较大的艏摇摆角有较好的性能，而在高进速时，较小的艏摇摆角有一定的优势。

（5）本阶段仅粗略探索了翼尖形状对性能的影响，现有结果还不能直接应用于工程实践，需要更细致的参数对比分析，而后经过试验验证，才能实现水翼参数化设计。