X形艉舵水下航行体变舵角水动力特性及其数学模型研究
陈纪军,潘子英,夏 贤,郑文涛
(中国船舶科学研究中心,江苏 无锡 214082)
0 引 言
操纵性是水下航行体综合航行性能中的重要内容,艉操纵面的布局选型与设计是操纵性的重要影响因素。相较十字形艉布局,X 形艉舵具有不超宽、降低舵卡严重后果等优点,近年来在世界各国的水下航行体上得到了发展与应用。由于X 形艉布局及其操纵的特殊性,关于X 形艉布局水下航行体的操纵性水动力特性,国内外学者们也开展了不少的研究工作。
在国外,加拿大DRDC 的Mackay[1]整理了1987~1988年间完成的十字形和X 形艉布局潜艇缩比尾段风洞模型试验结果,内容包括尾段位置力和单独艉操纵面的压力测量,较为系统地获得了两种不同艉布局方案的舵角和姿态角的耦合试验数据,该报告试验数据量非常庞大,但较为遗憾的是关于试验数据的分析及其结论公开极少,同时该研究中开展的压力测量试验仅仅是针对艉操纵面的,未对尾段表面,尤其是与艉附体紧邻的艇体表面压力分布进行测量。Bettle[2]采用数值计算与经验公式相结合的方法,对具有不同面积的X形艉舵方案操纵性能进行了预报,评估分析了达到期望操纵性指标的操纵面面积大小,该研究中的舵角相关水动力直接采用了理论方法,在对无界均匀流中舵水动力预报的基础上进行了修正估算。意大利CNR 的Broglia 等[3]针对不同面积的十字形和X 形艉布局潜艇在深水及近水面时水平面内非定常PMM 运动的水动力进行了数值模拟,并对比评估了两方案的稳定性,但未就舵角相关的水动力特性及其建模开展进一步的研究与分析。
在国内,针对X 形舵操纵不直观的特点,张涛、林俊兴[4]通过理论分析,分别给出了X 形舵在相同舵面积、不同舵面积时与十字形舵的等效关系;胡坤等[5-6]在回顾世界各国X 形舵潜艇发展概况基础上,分析了X 形舵潜艇操纵性水动力(矩)和控制方法,提出了X 形舵与十字形舵等效舵角转换装置设计思想,并采用数值仿真比较了X 形舵和十字形舵的操纵特性,提出了今后工作中待解决的四点问题,其中有三条是关于X形艉布局潜艇水动力特性的研究;吴军[7]基于理论计算,比较了十字形及X形艉布局的操纵特性;张露等[8]采用数值计算方法,比较了面积相等的十字形与X 形艉布局水下航行体的水动力特性,包括直航阻力与不同攻角状态的升力;陈纪军等[9]采用数值计算方法,比较了面积相等的十字形与X形艉布局水下航行体的操纵性水动力特性。
综上,国内外学者已针对X形艉布局的水下航行体操纵性水动力特性开展了研究。但是,现有研究中关于X 形艉布局方案的水下航行体变舵角水动力特性及其数学建模的文献并不多,而该部分研究工作是X 形艉布局水下航行体采用基于数学模型的操纵运动预报研究方法的基础。因此,开展X形艉布局水下航行体舵角相关的水动力特性及其数学模型研究对其操纵性能的准确预报及分析评估具有重要的研究意义。
有鉴于此,本文以基于SUBOFF 的X 形艉布局为研究方案,通过数值计算分析该布局方案变单舵、同变双舵及差动变舵时的非线性操纵性水动力特性,并对舵导数进行拟合研究,在现有船标线性模型基础上[10],对X形艉布局水下航行体变舵角相关的水动力项进行增补。
1 研究对象
研究对象基于SUBOFF进行了改型,如图1所示,由主体、围壳及艉操纵面(四个全动舵,由SUBOFF 十字形方案顺时针旋转45°得到,各舵按编号1~4 标识)构成,不包括导管及支柱。主要参数列于表1[11]。

图1 研究对象Fig.1 Research object

表1 研究对象主要参数Tab.1 Main parameters of research object
2 数值计算简介
2.1 X舵舵角定义
图2 给出了本文计算研究涉及的舵2 及舵3 的舵角定义,按各舵尾缘朝下偏转为正,各工况对应的侧向力Y、垂向力Z、纵倾力矩M、偏航力矩N按照通用艇体坐标系定义[10]。

图2 X舵舵角定义(左:正;右:负)Fig.2 Definition of X-rudder angle(Left:positive;Right:negative)
2.2 计算策略简述
本文数值研究的计算域大小、网格生成参数、边界条件定义等与文献[9]中的计算策略完全一致,针对SUBOFF的操纵性水动力已与文献[11]的模型试验结果进行了验证。这里,计算策略简述如下:
(1)数值计算域为长方形,前方和侧面均为2倍艇长,后方为3倍艇长,如图3(a)所示;(2)网格生成参数如表2所示;

表2 网格生成参数Tab.2 Main parameters of mesh generation
边界条件定义如下:
a.入口——模型前方和侧面定义为速度入口,设定速度为2.93 m/s,湍流强度取2%,湍流粘度比取2;
b.出口——模型后方定义为压力出口,湍流强度及粘度比与入口定义相同;
c.物面——定义为静止,无滑移。
整个计算域采用棱柱六面体网格划分,网格总数约180万,模型表面网格划分如图3(b)所示。
控制方程包括时均的连续方程及N-S 方程,并采用湍流模型RNGk-ε封闭。
数值计算时以体积力模拟螺旋桨的抽吸,如图3(c)所示,这里,螺旋桨水动力特性模型采用软件默认的5叶桨模型[12],正式计算前根据研究对象直航阻力、螺旋桨推力间的平衡进行了匹配,确定了体积力模型的主要参数,详见表3。

表3 螺旋桨体积力模型主要参数设置Tab.3 Main parameter setup for body force model of propeller

图3 数值计算描述Fig.3 Description of the numerical calculation
2.3 计算结果处理
针对SUBOFF的X形艉布局方案,采用数值方法计算的操纵性水动力按公式(1)作无因次化处理:

式中:ρ为流体介质密度,取997.561 kg/m3;U为入口合速度。
3 计算结果及分析
本文主要通过数值计算研究分析X形艉舵水下航行体变艉舵相关的操纵性水动力特性。由于在舵角超过一定值后,可能会出现失速,为了使得计算研究结论具有一定的普适性,且考虑到本文研究对象舵展弦比较小,因此确定本次计算最大舵角为20°。
3.1 变单舵操纵性水动力特性研究
首先针对舵3,基于上述策略生成的网格,开展了变单舵的操纵性水动力数值计算。舵角变化范围为δ3=-20°~+20°,Δδ3=10°,数值计算结果如图4所示。
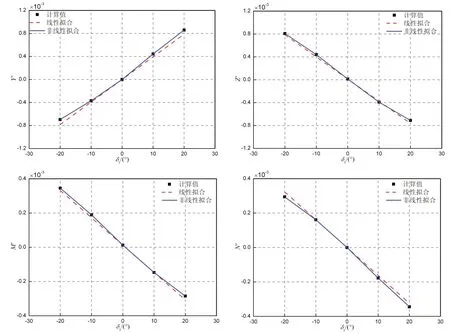
图4 变单舵数值计算结果Fig.4 Computational results of single rudder case
由图4 可见,随着舵3 舵角的增大,整体操纵性水动力/矩呈单调变化。但需注意的是:同一舵角下,水平面和垂直面内的水动力分量(Y'与Z')、矩分量(M'与N')并不是简单按照45°分解成相同的两个分量,彼此间存在着较大的差异;舵角角度相同,符号相反时,同一方向水动力(矩)也存在着明显差异。以δ3=±20°的水动力为例,表4给出了水下航行体各部件的操纵性水动力量值的统计对比,以分析上述差异原因。

表4 各部件水动力对比Tab.4 Comparison of hydrodynamic forces on each part
由表4 可见:(1)当舵3 的舵角相同,但符号相反时,舵3 水动力量值变化显著。同时主体上的水动力变化也较为明显,其他部件力基本不变(相较主体及舵3差了一个量级甚至更高);(2)定量上,当δ3=+20°时,水下航行体所受的垂向力Z'较侧向力Y'减小约16%;当δ3=-20°时,垂向力Z'较侧向力Y'增大约16%。
图5分别给出了两个舵角时尾部的流线及压力云图对比。由图可见,当δ3=+20°时,在舵3的吸力面侧产生了较大的流动分离(低压区),该流动分离同时影响了主体及舵3 的表面,同时,由于该分离区域是在舵3的上侧,从投影面来讲,该流动分离在水平面的贡献要高于垂直面,即主体及舵3在水平面产生的侧向力要大;反之,当δ3=-20°时,流动分离(低压区)位于舵3 的下侧方向,根据投影,该流动分离在垂直面的贡献要高于水平面,即主体及舵3在垂直面产生的垂向力较大。综上,由于有舵角时舵与主体尾部间的相互作用,产生了前述的两点差异。

图5 变单舵时尾部速度流线及压力云图比较Fig.5 Comparison of velocity streamlines and pressure contours on the after body for single rudder
现有的船标文件给出了单独变舵角相关的水动力线性拟合表达形式[10],如公式(2)所示:

式中,F'代表各水动力(矩)分量的无量纲形式,即Y、Z、M、N,按此线性拟合的各系数见表5。根据该系数,可反算各舵角的拟合值(见图4)。由图4可见,因不同方向力(矩)的线性导数项量值相当,反算的各方向力(矩)系数拟合值基本相当,但与计算值间存在较大差异,尤其是在大舵角情形,不能反映同舵角时垂向力与侧向力的差异,以及舵角角度相等但符号不同时同一力(矩)分量的差异。
因数学模型的准确与否直接关系水下航行体操舵运动响应的预报精度,进一步地,考虑各水动力(矩)随舵角的单调特性,并考虑正负舵角时的不对称项,参考潜艇垂直面变攻角时位置力的非线性拟合表达[13],按如下作非线性拟合:

按公式(3)拟合获得的各系数见表5,根据该系数反算各舵角的拟合值见图4。由图4 可见,相较线性拟合,考虑了非对称影响的非线性拟合与计算值吻合较好,很好地反映了水动力(矩)随舵角的变化特点。

表5 变单舵水动力系数拟合Tab.5 Fitting of hydrodynamic coefficients of single rudder
3.2 同变双舵操纵性水动力特性研究
进一步地,开展了同变舵2 和舵3 的操纵性水动力数值计算。舵角变化范围为δ2=δ3=-20°~+20°,Δδ2=Δδ3=10°。
区别于变单舵3,同变舵2和舵3时左右舵产生的侧向力Y'及偏航力矩N'相互抵消,因此,对于操纵性整体力而言,仅可关注垂直面的垂向力Z'及俯仰力矩M'。不同舵角下的数值计算结果如图6 所示,图中同时给出了单变舵2和舵3的垂向力Z'及俯仰力矩M'的线性叠加。

图6 同变舵2、舵3数值计算结果Fig.6 Computational results of same double rudders
由图6 可见:(1)垂向力Z'及俯仰力矩M'随舵角呈单调变化,相较同变正舵角,当同变负舵角时,水下航行体所受的垂向力Z'及俯仰力矩M'较大,定性上与变单舵是一致的;(2)相较变单舵2 和舵3的线性叠加,同变双舵产生的垂向力Z'及俯仰力矩M'略高,这在负舵角时更为显著。
以同变-20°和+20°为例,两工况的表面压力分布及尾部流线比较如图7 所示。由该图可见,当同变-20°时,在舵2和舵3的下部存在流动分离,形成低压区;当同变+20°时,在舵2和舵3的上部存在流动分离,形成低压区。低压区的存在同时影响了主体及舵2、舵3的表面压力,与变单舵3相同,由于两低压区位置的不同,根据投影,相较同变+20°工况,当同变-20°时,其在垂直面内影响较为显著,这也直接使得该工况下整体所受的垂向力Z'及俯仰力矩M'较大。
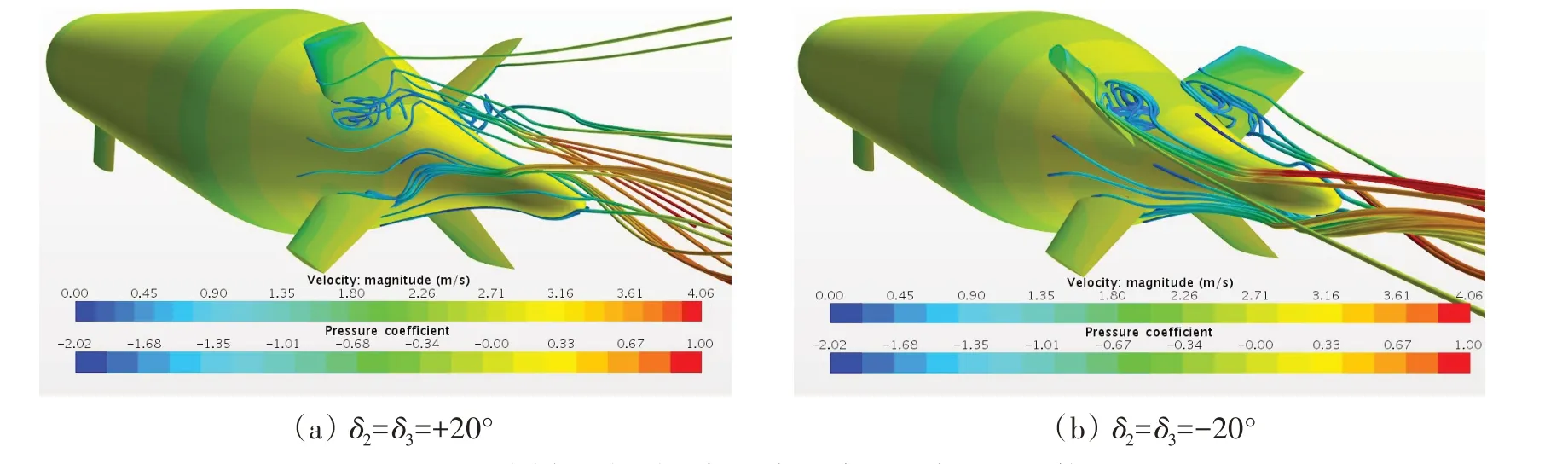
图7 同变双舵时尾部速度流线及压力云图比较Fig.7 Comparison of velocity streamlines and pressure contours on the after body for same double rudders
进一步地,以舵角-20°为例,对比分析了变单舵和同变双舵时各部件的垂向力Z',见表6。图8给出了该舵角下变单舵和同变双舵时尾部下方的压力云图对比。结合表6和图8,由于变单舵时没有能够形成较为完整的“狭道”,因此变单舵时主体及舵3上的力略小。

图8 变单舵与同变双舵压力云图对比(左:δ3=-20°;右:δ2,3=-20°)Fig.8 Comparison of pressure contours on the after body(Left:δ3=-20°,Right:δ2,3=-20°)

表6 各部件水动力统计Tab.6 Comparison of hydrodynamic forces on each part
与变单舵类似,参考式(2)~(3),同变双舵的操纵性水动力分别按式(4)~(5)拟合:
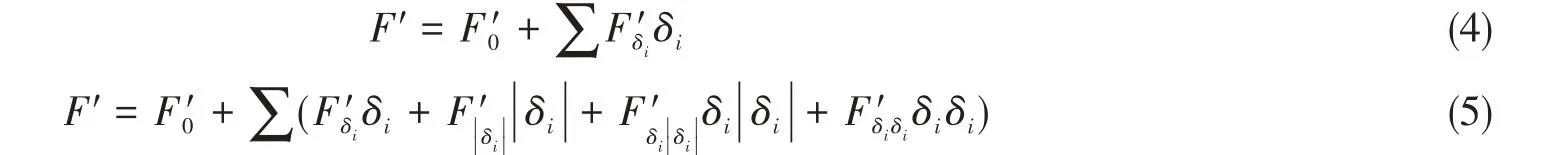
式中,i=2,3。由于左右对称,舵2 和舵3 在垂直面内的力/矩相关导数量值和符号相同,如F'δ3=F'δ2。按此进行拟合得到的导数列于表7,不同模型反算的拟合值绘于图4。

表7 同变双舵水动力系数拟合Tab.7 Fitting of hydrodynamic coefficients of same double rudders
与前述类似,相较线性拟合,采用式(5)的非线性拟合,较好地反映了同变双舵时不同舵角下的操纵性水动力特性。
3.3 差动变舵操纵性水动力特性研究
区别于十字形艉布局上下、左右同变舵特点,X 形艉舵布局具有高度的自主性,各舵可能出现差动变舵情形。这里仍以下两舵为例,基于上述网格,系列开展了差动变舵2、舵3的操纵性水动力数值计算,初步探讨分析了舵-舵间的相互作用。数值计算时,固定舵3,系列改变舵2的角度,计算工况列于表8。

表8 计算工况Tab.8 Computational cases
差动变舵的数值计算结果如图9所示。


图9 差动变舵数值计算结果Fig.9 Computational results of different double rudders
同样地,类似式(2)~(5),差动变舵2、舵3 的操纵性水动力按式(6)~(7)进行了拟合,拟合获得的水动力导数见表9,按式(6)~(7)拟合的曲线如图9所示。
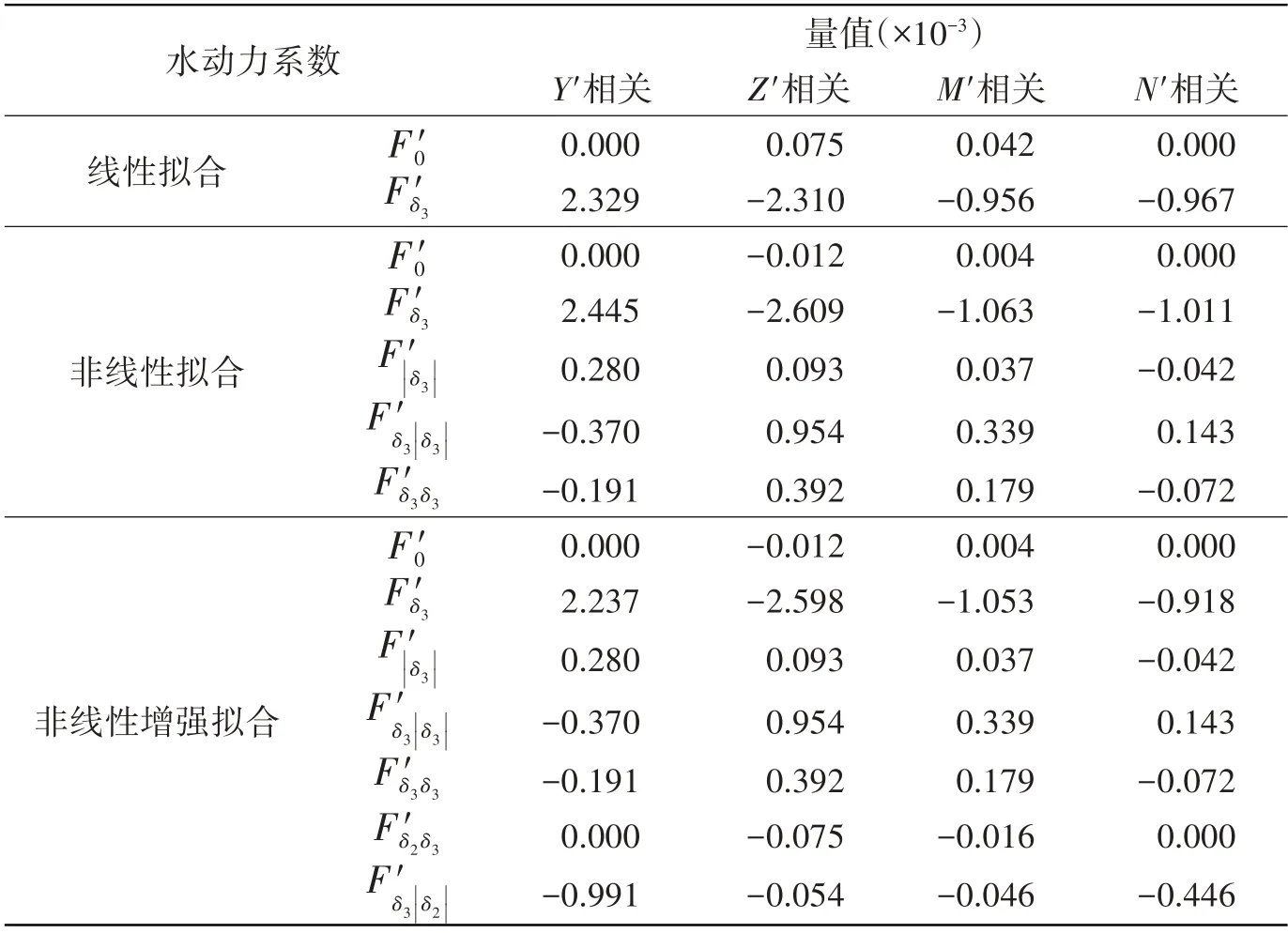
表9 差动变舵2、舵3水动力系数拟合Tab.9 Fitting of hydrodynamic coefficients of different double rudders
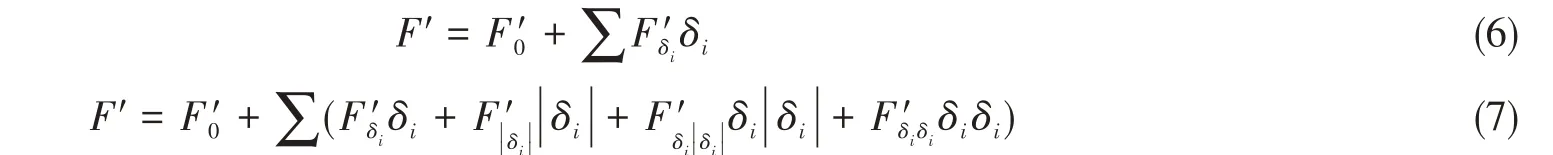
式中,i=2,3。由图可见,与前述类似,相较线性拟合,除个别点外,采用非线性拟合可较好地反映差动变舵时的操纵性水动力特性。
进一步地,在式(7)基础上增加相关项,以表征舵2和舵3间的相互干扰,如式(8)所示:

式中,i=2,3。根据该非线性增强拟合获得的各水动力系数参见表9,由该水动力系数计算的差动变舵的拟合曲线见图9。由图9可见,考虑这三项后,整体拟合效果得到了进一步的改善。
为定量评估三种拟合方法相对于计算原始值的拟合效果,以各计算点拟合值与计算值差的平方和(即残差平方和)来表征拟合的好坏[14],即
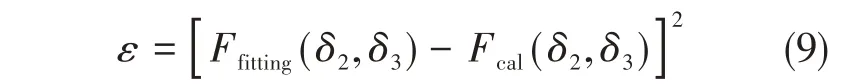
采用不同拟合方法获得的各分量残差平方和统计如表10所示。
由表10 可见,针对各力、矩分量,采用非线性增强拟合效果最优。总体而言,相较线性拟合,当在非线性拟合模型基础上进一步考虑舵与舵间的相互干扰项时,可在一定程度上改善各操纵性水动力的拟合效果。

表10 不同分量的残差平方和统计Tab.10 Residual statistics of different hydrodynamic force coefficients
4 结 论
本文以基于SUBOFF 的X 形艉布局为研究对象,通过数值计算分析了该布局方案变单舵、同变双舵及差动变舵时的操纵性水动力特性,并通过拟合研究,比较分析了变舵角相关的水动力项线性和非线性数学模型表达。主要研究结论如下:
(1)变单舵时,同一舵角下,水平面和垂直面内的水动力分量(Y'与Z')、矩分量(M'与N')存在着差异;变单舵或同变双舵时,当舵角角度相同、符号相反时,同一方向水动力(矩)量值存在着明显差异。经分析,上述差异是由于X舵和主体尾部间存在的相互作用在垂直面、水平面内的投影不同所导致;
(2)相较单变舵2和舵3的水动力线性叠加,同变双舵产生的垂向力Z'及俯仰力矩M'略高;
(3)相较船标中仅给出了变舵角相关的线性项,增加非线性项可较好地反映X形艉布局航行体变单舵、同变双舵时整个变化舵角范围内的水动力特性;
(4)差动变舵时的操纵性水动力特性较为复杂,在非线性拟合模型基础上进一步考虑舵与舵间的相互干扰项时,可在一定程度上改善各操纵性水动力的拟合效果。
本文工作可为X形艉布局水下航行体操纵运动(如变同侧双舵)数学建模以及操纵特性分析提供支撑。后续可通过开展X形艉舵的水下航行体主体尾部及舵表面的压力测试分析进一步验证前述相关结论。

