水面泵喷推进自航因子数值与试验研究

孙小帅，马 骋，钱正芳，韩用波，程红蓉

（1.中国海洋开发研究中心，北京100161；2.中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

泵喷推进器由转子、定子和导管组成，具有推进效率高、抗空化性能好、临界航速高、水下辐射噪声低等优点[1]。根据定子与转子相对位置的不同，可以分为前置定子泵喷和后置定子泵喷。其中前置定子泵喷的定子可以预旋流场，使定子和转子产生的尾流旋转能量相互抵消，其噪声较低，广泛应用于核潜艇推进，如美国海浪级、弗吉尼亚级、英国机敏级核动力潜艇等；后置定子泵喷的定子可以吸收转子尾流场的能量，提高推进效率，并可平衡转子扭矩，主要应用于鱼雷推进，如美国MK48鱼雷等。

在泵喷推进器的研究初期（上世纪五十年代左右），美国海军曾分别在一艘试验驱逐舰USS Witek和一艘反潜驱逐舰USS Glover 上安装后置定子泵喷，但后续并未大规模推广应用，其主要原因是当时的设计水平偏低，泵喷的性能优势未发挥出来[2]。近些年来，随着泵喷推进器研究的不断深入和设计水平的逐渐提高，为充分发挥泵喷推进器的性能优势，又出现了将其应用于水面船舶的研究。

美国海军在电船演示舰AESD 上使用了由Rolls-Royce 公司研发的水面泵喷推进器，主要结构由转子、定子、导管和倒车机构组成，具有推进效率高、辐射噪声低的特点[3]。与传统泵喷推进器相比，其导管较长并融入船体，可以起到更好的整流作用，对提升抗空化性能有利，根据其导管特点将其命名为长导管水面泵喷推进器。曹玉良等[4]采用三元理论设计了两型长导管水面泵喷推进器，运用粘性计算流体力学CFD方法分析了该推进器在船后的水动力性能和抗空化性能；彭云龙等[5]运用三元理论设计了长导管水面泵喷推进器，针对实尺度模型采用粘性计算流体力学CFD 方法分析了船体对推进器水动力性能的影响;易文彬等[6]开展了长导管水面泵喷推进器的自航试验，同时基于CFX 软件开展了自航工况的数值模拟，计算结果与试验结果吻合较好。

近年来德国Voith 公司研发了另一种水面泵喷推进器——Linerjet，主要结构由转子、定子和导管组成，在较大的航速范围内具有较高的推进效率，抗空化性能优良，已推广应用于多艘船艇[7]。与传统泵喷推进器相比，其导管较短并嵌入船底，因而适用于浅水环境，应用该推进器时需与船底外形开展匹配设计。根据其导管特点将其命名为短导管水面泵喷推进器，目前国内外对其进行研究的公开文献十分少见。

本文针对一条安装短导管水面泵喷推进器的三体船模型，采用计算流体力学CFD方法，开展裸船体阻力试验、全附体模型阻力试验、推进器敞水性能试验和自航试验数值模拟，并在拖曳水池开展裸船体阻力试验和自航试验，分析船体航行姿态对阻力预报的影响、附体对全船阻力的影响、短导管水面泵喷推进器与船体之间的相互作用和推进器转子叶片的水动力，研究结果可为短导管水面泵喷推进器的设计提供技术支撑。

1 数值研究

1.1 流动控制方程

计算流体力学CFD方法由于方程本身可以计入粘性和非线性的影响，可以更好地处理湍流、波浪破碎等非线性水动力问题[8]，在船舶的快速性、操纵性和耐波性分析中被广泛应用。粘性流动控制方程包括连续性方程和动量方程[9]，分别为

式中，ρ为流体密度，μ为流体粘度，p为静压，fi为单位质量力，uˉi、uˉj为平均速度分量，ρ-- --u′iu′j为雷诺应力。

为了平衡计算精度和计算时间，采用RANS 方法求解控制方程，湍流模型选用在工业领域广泛应用的Realizablek-ε模型。壁面处理采用全y+处理方法，根据y+值的大小自动选择处理方式，当y+＜1时直接求解粘性底层流场，当y+＞30 时使用壁面函数求解边界层流场，当1＜y+＜30 时使用混合函数求解边界层流场。使用通用流体力学求解器Starccm+采用有限体积法对流动控制方程对其离散和求解，使用二阶离散模式来提高计算精度。自由液面捕捉采用VOF（volume of fluid）方法，其方程为

式中，q=1、2，a1和a2分别为空气相和水相的体积分数。

1.2 运动模拟方法

航行姿态对船舶航行阻力有重要影响。对中高速排水型船，若不考虑升沉和纵倾等航行姿态的变化，阻力预报的误差可超过10%[10]。在进行船舶阻力和自航数值模拟时，计入升沉和纵倾的变化。使用六自由度运动求解器DFBI（dynamic fluid body interaction）和整体网格运动技术求解船体运动，释放船体的升沉和纵倾两个自由度，约束其他自由度的运动。进行数值模拟时针对船体表面划分网格，求解作用在船体表面的力和力矩。调整船体升沉和纵倾，直至船体的纵向运动达到稳态。

水面泵喷推进器转子的旋转运动模拟采用动网格法。在转子附近建立旋转域，数值模拟时整个旋转域按照指定的角速度旋转。旋转域与周围的流场之间建立交界面，通过插值传递速度、压力等流场数据。

1.3 自航因子求解方法

为求解自航因子，分别开展船体阻力试验、推进器敞水性能试验和船体自航试验数值模拟。开展自航数值模拟时，参考强制自航法使强制力Z=FD（FD为摩擦阻力修正值）。

式中，Cfm为船模的摩擦阻力系数，Cfs为实船的摩擦阻力系数，ΔCf为换算补贴系数，ρm为模型试验时的水密度，Sm为船舶湿表面积，Vm为船模航速。

为快速获得模型自航点，编写用户自定义函数，根据船体受到的推力、阻力和强制力之和自动调节转子转速，直至船体受力达到平衡状态[11]。

1.4 数值船模与边界条件

计算对象为三体船，该船安装了两个短导管水面泵喷推进器。水面泵喷推进器由短导管、转子和后置定子组成，转子叶数为7叶，转子直径为0.133 m，定子叶数为13叶，导管长度为0.133 m，导管入口直径为0.148 m，导管出口直径为0.133 m。计算对象的三维图和主要参数如图1和表1所示。

图1 三体船示意图Fig.1 Trimaran model

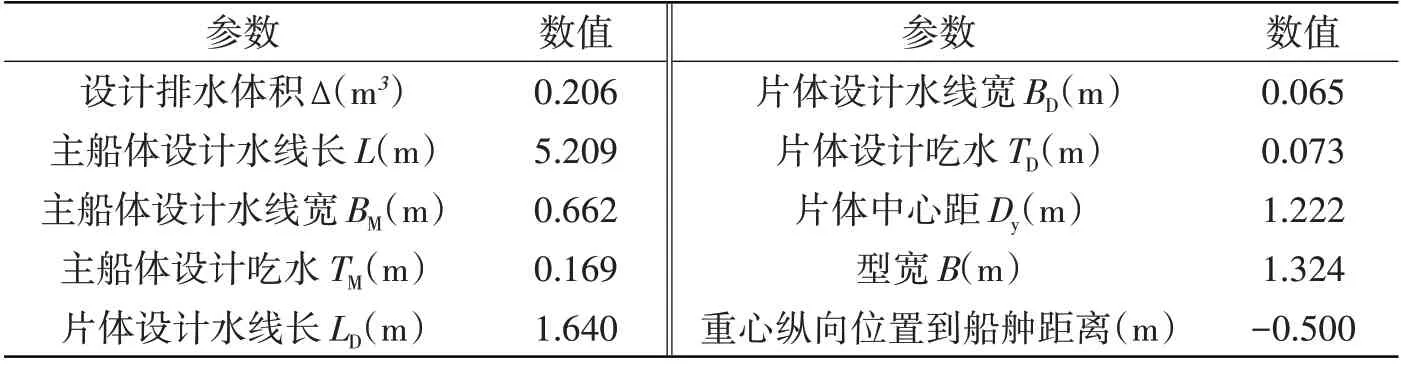
表1 船体主要参数Tab.1 General properties of the trimaran model

图2给出了计算域和边界条件设置。整个计算域的长宽高分别为6.5L、1.5L和2.5L。为提高计算效率，针对半船划分网格并开展粘性流场模拟。计算域的出口设置为压力出口，右侧设置为对称面，其他边界设置为速度入口。船体表面设置为无滑移壁面。

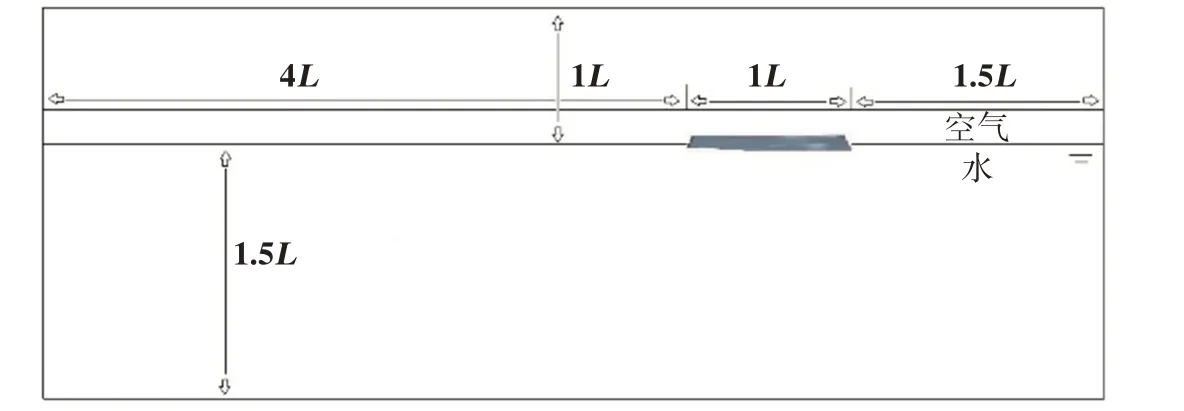
图2 计算域Fig.2 Fluid domain

网格划分采用非结构六面体剪切型（trimmer）网格，在船体表面设置10 层边界层，调整第一层网格厚度使船体表面大部分y+值处于30～200之间。对船体艏艉、推进器和自由液面附近区域的网格进行加密，以便更好地捕捉流场细节。整个计算域网格数量为212 万，其中旋转域网格数量约为58 万，船体表面、推进器转子和定子的网格划分情况如图3所示。

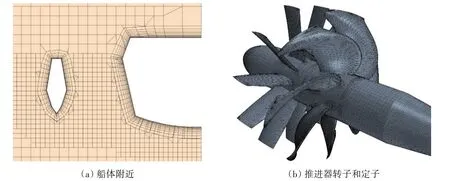
图3 网格划分Fig.3 Meshes

2 试验研究

在中国船舶科学研究中心拖曳水池开展裸船体阻力试验和全附体模型自航试验（如图4 所示）。试验模型为木模，几何线型与数值船模一致。在阻力试验和自航试验时，船模均可以自由升沉和纵摇。进行阻力试验时采用四自由度适航仪，纵摇运动的量程为±30°，升沉运动的量程为±300 mm，阻力量程为±300 N，测量精度为0.1%。

图4 试验模型Fig.4 Experimental trimaran model

自航试验时采用强迫自航法，使用R31 自航仪，推力量程为100 N，扭矩量程为4 N·m，测量精度为0.1%。在推进器推力和强制力的共同作用下，船模前进速度和拖车速度保持一致。导管、定子与船体刚性连接，自航仪测量转子的轴向推力和扭矩。

3 结果与分析

分别对裸船体阻力试验、全附体阻力试验、推进器敞水性能试验和自航试验进行数值模拟，数值计算时的弗劳德数Fr为0.147-0.590。

3.1 阻力性能

图5 给出了裸船体（不带推进器和轴）单位排水量阻力随弗劳德数Fr的变化，其中固定是指约束船体姿态保持正浮的工况，自由是指释放船体升沉和纵倾两个运动自由度的工况。通过对比可以发现，数值计算的裸船体阻力略小于试验结果，最大误差出现在Fr= 0.442 时，误差为-2.84%。与释放船体升沉和纵倾时的阻力试验值相比，固定船体不动时的阻力计算值在中高速时偏小约13.08%～25.89%，特别在高速时偏差较大，表明预报高速船阻力时计入船体姿态的影响是十分必要的。

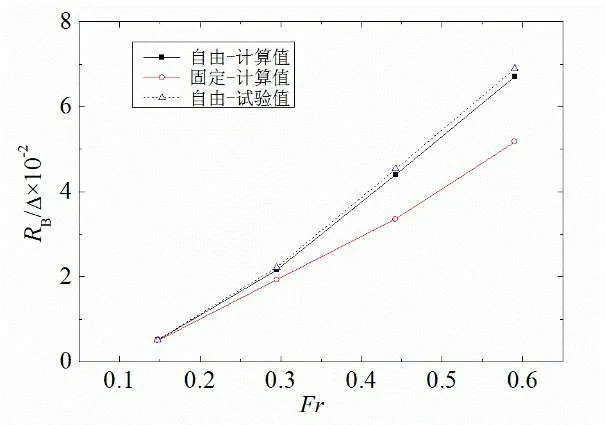
图5 裸船体阻力对比Fig.5 Resistance of bare trimaran

表2给出了裸船体升沉和纵倾的数值计算结果，其中升沉为负表示下沉，纵倾为负表示艉倾。可以发现，在不同的Fr时，船体均有所下沉，且均呈现出艉倾姿态。随着航速的增大，船体的下沉先增大后减小，而艉倾呈现出增大的趋势，艉倾角最大时达到1.022°。

表2 裸船体升沉和纵倾Tab.2 Sinkage and trim of bare trimaran

图6 给出了全附体船体（裸船体+轴+导管+定子，不含转子）单位排水量阻力随弗劳德数Fr变化的数值计算结果。可以发现，裸船体安装导管、定子和轴之后，全船阻力大幅增加。在Fr=0.147 时增加约32.92%，在Fr=0.295～0.590时增加19.18%～21.50%。

图6 全附体船体阻力数值计算结果Fig.6 Numerical results of resistance of bare trimaran with stator,duct and shaft

3.2 推进器敞水性能

进行推进器敞水性能模拟时，进速系数范围为0.2～1.8，转子的转速保持20 r/s不变，改变来流速度调整进速系数。

图7给出了水面泵喷推进器的敞水性能曲线。可以发现，推进器整体的推力可以分为两部分：一是转动的转子所产生；二是静止的导管和定子所产生。其中转子产生的推力是主要的，随着进速系数增大，转子对整体推力的贡献从60.46%上升至188.42%。在进速系数J=0.2～1.3时，导管和定子提供一定的推力，随着进速系数继续增大，导管和定子的受力变为阻力。导管和定子上的扭矩相对较小，约为转子扭矩的31.66%～56.01%。推进器敞水效率在J=1～1.4范围内均大于60%，在J=1.2时达到最大，效率最高为63.37%。

图7 推进器敞水性能Fig.7 Open water characteristics of the propulsor

3.3 自航点

开展自航试验数值模拟时，先保持推进器转子固定，待船体航行产生的兴波流场稳定后，转子开始旋转。通过自定义函数调节推进器转速，当推进器推力加上强制力与船体阻力平衡时，则该转速为自航点。弗劳德数Fr分别为0.147、0.295、0.442 和0.590 时，三体船模型自航点处推进器的转速Nm分别为6.42 r/s、12.77 r/s、17.97 r/s和22.76 r/s。

表3 给出了三体船模型推进器自航转速、转子轴向推力和扭矩的数值计算结果和试验结果。数值计算求解的三体船模自航转速略大于试验值，转子轴向推力在中高速时略小于试验值，轴向扭矩的计算结果小于试验值。在高速（Fr=0.442-0.590）时，转速的计算误差小于4.36%，转子轴向推力误差小于1.62%。总体来看，数值计算结果与船模试验结果吻合良好。

表3 自航点时转子的推力和扭矩Tab.3 Thrust and torque of the rotator at self-propulsion state

3.4 自航因子

将转子、定子和导管作为推进器求解推力减额、伴流分数等自航因子。计算自航点处的无量纲参数:J=Vm/NmDm，KT=Tm/ρmN2mD4m，KQ=Qm/ρmN2mD5m。按照等推力法，在推进器敞水性能曲线上根据KT=KT0，求解得到J0、KQ0和η0，则船模的实效伴流分数wm=1-J0/J，相对旋转效率ηR=KQ0/KQ。再根据裸船体的阻力数据Rm，可以得到推力减额tm=（Tm-Rm+FD）/Tm，进而得到船身效率ηH=（1-tm）/（1-wm），推进效率ηD=ηRηHη0。

在水池开展自航试验时，导管和定子与船体刚性连接，仅测量转子轴向的推力和扭矩，难以分离出导管和定子上的受力。采用CFD方法进行自航试验数值模拟时，可以分离船体、定子和导管各部分的受力，得到推进器总推力，进而计算自航因子。

表4给出了根据自航试验数值模拟结果求解的推力减额tm、伴流分数wm、敞水进速系数J0、敞水效率η0、相对旋转效率ηR、船身效率ηH和推进器效率ηD。可以发现，随着弗劳德数增加，推力减额呈现降低的趋势，伴流分数呈现增加的趋势，总推进效率不断增大。在高速（Fr=0.442～0.590）时，推力减额约为0.055～0.058，伴流分数约为0.049～0.065，推进效率约为0.567～0.574。

表4 自航因子计算结果Tab.4 Results of propulsion factors

3.5 船体和推进器水动力分析

表5 给出了弗劳德数Fr为0.590 时，三体船模在不安装转子（安装导管、定子和轴）和安装转子并以自航点转速旋转两种工况分别在航行方向受力的数值计算结果，其中负值表示该部件提供推力。可以发现，没有安装转子时，定子和导管均产生阻力；当安装转子并旋转时，在转子的作用下，船体受到约11.37%的阻力增加，定子产生一定的推力，约为转子推力的1.76%；导管产生的阻力大幅下降，约为转子推力的2.86%。

表5 船体在不同工况时的受力Tab.5 Hydrodynamic force of the hull at different states

图8 给出了转子旋转360°时各个叶片产生推力的变化。可以发现每个转子叶片在旋转一周的过程中产生的推力是波动的，波动幅值约为每个叶片平均推力的33.12%。

图8 转子叶片在旋转过程中产生的推力Fig.8 Thrust of the rotator during one round

3.6 流场分析

图9 给出了弗劳德数Fr=0.590 时船尾兴波的数值模拟结果和试验结果。水面泵喷推进器在水下喷射水流，从船尾下方向后流动，在距船尾约0.2倍船长处开始抬升。

图9 船尾兴波对比Fig.9 Comparison of stern waves

4 结 论

本文针对一条安装短导管水面泵喷推进器的三体船模型，采用计算流体力学CFD 方法开展了裸船体阻力试验、全附体模型阻力试验、推进器敞水性能试验和自航试验数值模拟，并在拖曳水池开展了裸船体阻力试验和自航试验，分析了船体航行姿态对阻力预报的影响、附体对全船阻力的影响，求解了自航点和自航因子，研究了推进器转子叶片旋转360°过程中推力的变化，得到的主要结论如下：

（1）航行姿态对中高速船的阻力预报具有重要影响，对于本文研究的三体船模，若不计入航行姿态的影响，阻力预报结果在中高速（Fr＞0.295）时将偏小13.08%～25.89%。

（2）短导管泵喷推进器在较大的进速系数范围内均可保持较高的敞水效率，本文研究的短导管泵喷推进器的敞水效率在J=1～1.4范围内均大于60%。

（3）由于短导管泵喷推进器和船底融合在一起，自航模型试验时难以分离导管、定子受到的水动力，采用数值模拟方法可以分析各部件的受力，进而求解自航因子。

（4）通过对比裸船体阻力、自航点转速、转子轴向推力和扭矩的数值计算结果和模型试验结果，可以发现数值计算求解的裸船体阻力误差小于2.84%，高速（Fr=0.442～0.590）时的自航转速误差小于4.36%，转子轴向推力误差小于1.62%，表明本文建立的数值计算模型是可靠的。在自航试验的数值模拟结果基础上，求得Fr=0.442～0.590 时的推力减额约为0.055～0.058，伴流分数约为0.049～0.065，推进效率约为0.567～0.574。