聚焦数学核心素养，培养学生数学思想——以“植树问题”为例

□广州市黄埔区黄陂小学 庄琪

教育部提出的立德树人的根本任务，是把核心素养和学业质量要求落实到各学科教学中。数学核心素养离不开数学的本质和数学思想，培养学生的数学思想，让学生会用数学的眼睛观察世界，会用数学的思维思考世界，会用数学的语言表达世界，是许多教师的目标。虽然不容易实施，但只要教师潜心教育，用心实施，一定能促进学生全面发展。

2014 年3 月，《教育部关于全面深化课程改革落实立德树人根本任务的意见》印发，提出“各级各类学校要从实际情况和学生特点出发，把核心素养和学业质量要求落实到各学科教学中”。史宁中教授在《推进基于学科核心素养的教学改革》报告中指出，“学生核心素养的培养，最终要落在学科核心素养的培育上”。“数学核心素养”一词也成为广大数学教师耳熟能详的词，《义务教育数学课程标准（2011 年版）》明确提出了10 个核心素养，但却没有加以阐释。马云鹏教授认为“数学核心素养可以理解为学生学习数学应当达成的有特定意义的综合性能力，核心素养不是指具体的知识与技能，也不是一般意义上的数学能力。

核心素养基于数学知识技能，又高于具体的数学知识技能。核心素养反映数学本质与数学思想，是在数学学习过程中形成的，具有综合性、整体性和持久性。”《礼记》中提到“君子之教，喻也。道而弗牵，强而弗抑，开而弗达。道而弗牵则和，强而弗抑则易，开而弗达则思。和易以思，可谓善喻矣。”“善喻”道出了教师的“教”的最高境界——教学生悟思想，教师的“举一”，学生学会“反三”。数学课堂教学生知识——授之以鱼，教学生解题方法——授之以渔，这些都可考查，可评价。授之以“喻”较前两样来说难多了，要靠学生在学习的过程中只可意会、不可言传地悟出来。“喻”对于一线教师来说就是要重视数学课堂培养学生的数学思想。如何培养学生的思想是需要教师在课堂教学中解决的一个难题。史宁中教授指出：数学教育的终极目标是，一个人学习数学之后，即便这个人未来从事的工作和数学无关，也应当学会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界（以下简称“三会”），数学核心素养的确定要基于这个目标。下面，笔者以人教版五年级上册数学广角“植树问题”为例，谈谈数学广角中培养学生思想的一点见解。

一、设悬念，以疑促思

“学起于思，思源于疑”思维总是由于问题引起的，问题是思维的原动力。现在的学生学习知识有多种途径，学生不再是白纸一张，而是拥有不同的见解。如何调动学生的学习兴趣，引发学生的思考，也是教师需要考虑的问题。课堂伊始，教师开门见山地抛出问题“对于植树问题，你已经知道些什么？你有什么问题？”“你知道其中的数学思想方法吗？”个别学生在校外培训机构学习了植树问题的知识，但校外机构的学习更多的是让学生记住公式，进行大量的解题训练，让学生掌握解题方法，对这部分知识能让学生学到的数学思想方法并不重视。学生只知其然，却不知其所以然，对所学内容更多地处在“授之以鱼”的状态，只会依葫芦画瓢，解决和所学例题一样的类型题，稍做变化，便束手无策。教师可以通过提问，激起学生的好奇心，如植树问题还有什么我们不知道的数学思想方法呢？让学生带着问题开始数学的探究之旅。

二、抛难题，化繁为简

课本例题（见图1）“同学们在全长100 米的小路一边植树，每隔5 米栽一棵（两端要栽）。一共要栽多少棵树？”再通过学生的对话“每隔5 米栽1 棵，共栽100 ÷ 5=20（棵）”“对吗？怎样检验呢？”得出画线段图检验，“100 米太长了，可以先用简单的数试试。”看例题这样的编排，不由得引发笔者的思考：例题为什么要用100 米的数据，不用20 米作为例题路长的数据？从20 米开始，接着再验证路长25 米、30 米……的植树棵数，这样不是由浅入深、循序渐进教学吗？这里蕴含编者什么意图？

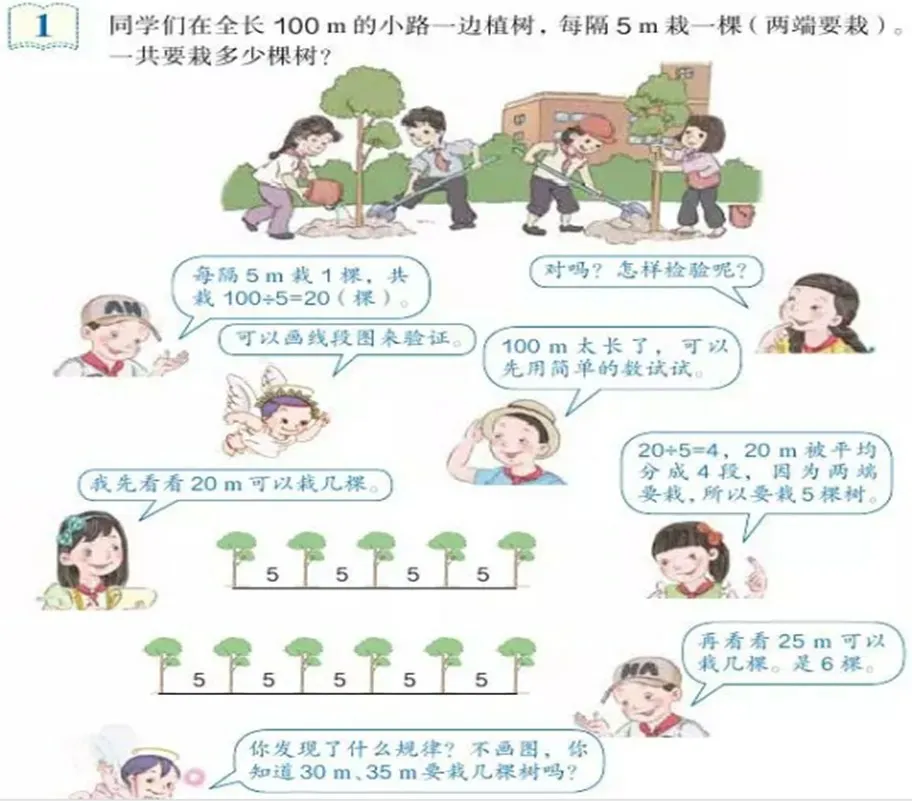
图1 教材例题图

带着这些疑问，笔者再次研读《教师教学用书》，从书中可以找到编者的意图：引导学生通过观察、猜测、试验、推理等活动，初步体会解决植树问题的模型思想，培养学生从实际问题中探索解决问题有效方法的能力。植树问题还承载着学生“化繁为简”“数形结合”“一一对应”“数学建模”和推理等数学思想。数学来源于生活。认知心理学认为：学生学习数学的认知过程，是一个把教材知识结构转化为自身数学认知结构的过程。100 米的小路植树比20 米更接近于生活实际，学生根据数据进行画图验证时，会觉得100 米数据太大，不好画图，从而引发学生的认知冲突，激发学生迫切要改小数据的欲望，让学生从解决生活实际问题中融会贯通：碰到不能或不容易用已有的知识解决问题时，尝试着把问题转化成已学或比较容易解决的问题，再进行解决。如果用较小的数据20 米、30 米……枚举验证，降低了难度，会导致学生体会不到化繁为简应用于解决问题的妙处，难于达成化归思想的渗透。

化归思想是数学分析问题、解决问题的一种策略和艺术，也是人人应该具备的数学素养。如果说数学思想是数学的灵魂，那么可以不夸张地说化归思想就是数学思想的核心，是数学思想的精髓。化归思想，是将一个问题由难化易，由繁化简，由陌生化熟悉，由抽象化具体的过程。化繁为简是化归思想一种重要的数学思想方法，在数学各个领域中都会用到。但平时的课堂中学生更多地处于被动接受的状态，让学生自发去做得相对少一些。在解读教材的设计意图后，笔者在设计例题时，特意把例题“同学们在全长100 米的小路一边植树”的数字由100 米调整为200 米。因为100 米的数据不大不小，对学生来说画20 格线段图也不是一件麻烦的事情，但是改成200 米，要画40 个格子学生就会觉得麻烦了，进而逼着学生用更简单的数据来推出规律，再根据规律算出大的数据的结果。

教学片段：

“同学们在全长200 米的小路一边植树，每隔5米栽一棵（两端要栽）。一共要栽多少棵树？”

教师：预测一下，可能种几棵树？

学生1：我认为40 棵。

学生2：我认为41 棵。

学生3：我认为39 棵。

教师：种树的棵数与什么有关？

学生4：路长和间距有关。

教师：怎样验证这个结果？

学生（集体）：画线段图。

教师：怎么画？画200 米吗？

学生5（摇头）：太麻烦了，画20 米。

教师：就只能画20 米吗？

学生：不是，可以画15 米、30 米、40 米……

教师：为什么找15 米、20 米、30 米、40 米？

学生：这些数都是5 的倍数。

……

通过例题数据调整为较大的数据200 米，让学生感到画图200 米存在困难，从而自觉地把大的数据转化成较小的数据进行解决，达到了化繁为简的目的，也让学生从中收获到在遇到比较复杂的问题时可以转化成已有的知识或较为简单的问题进行解决，达到授之以“喻”的教学效果。

三、解问题，数形结合

如果说化归思想是数学思想的核心，是数学思想的精髓。数形结合就是化归思想中实现从抽象化到具体的过程的重要桥梁。数形结合是数学解决问题中必不可少的思想方法。“数缺形时少直观，形少数时难入微，数形结合千般好，数形分离万事休。”我国数学家华罗庚道出数形结合的重要性。

学生用画线段图验证结果，就是数形结合帮助学生理解题意，验证方法。学生每个人都举2～3 个数据例子，进行画图尝试，验证结果，发现规律。学生发现20 米的路长，4 个间隔，植树5 棵（见图2）；25米的路长，5个间隔，植树6棵；30米的路长，6 个间隔，植树7 棵……并根据发现的规律完成表格（见表1）。

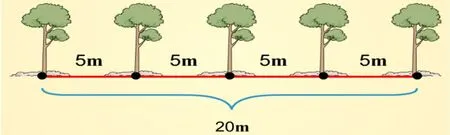
图2 学生探究过程图

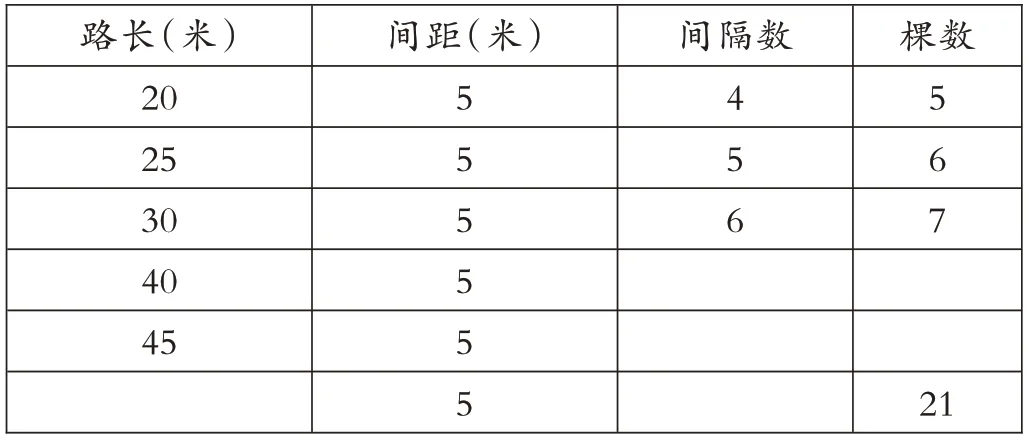
表1 学生探究过程表

通过数形结合，再让学生在画一画、圈一圈，用一一对应的方法发现规律，总结出两端都栽的方法：

路长÷间距=间隔数；间隔数+1=棵数。

学生用总结出的规律求出：

200 ÷ 5=40；40+1=41（棵）。

对于抽象的植树问题，学生通过画一画、圈一圈，用数形结合、一一对应的思想方法发现规律，降低了学习的难度，在解决问题中体会到了数形结合的方法带来的成功和解决问题的乐趣。

四、促迁移，建立模型

《义务教育数学课程标准（2011 年版）》在前言中指出：在数学课程中，应当重视发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。模型思想的建立是学生体会和理解数学与外部世界联系的基本途径，建立和求解模型的过程有助于学生初步形成模型思想，提高学习数学的兴趣和应用意识。由此可见，模型思想在培养学生数学素养中有着重要的意义，模型思想的渗透能够帮助学生了解数学与生活的联系，感受数学应用价值，同时提升学生的思维抽象水平。“植树问题”最重要的数学思想就是模型思想，让学生从实际问题中抽象出植树问题的模型是教学的难点。教材用形象的植树线段图过渡到抽象的线段图教学，利用几何直观地帮助学生理解两端都栽的植树问题的模型，让学生通过画20 米、25 米……的线段图，圈一圈棵数与间隔数，用数形结合、一一对应的思想方法发现棵数总比间隔数多1 的规律。学生抽象出两端都栽的植树问题的模型：间隔数+1=棵数，并能迁移运用到公共汽车站（地铁站）的设立，架设电线杆、路灯的安装，爬楼梯、敲钟、锯木头等问题上。用线段图直观地帮助学生理解植树问题的模型思想，还有一大好处：学生能看图得出两端都栽植树问题模型的逆运用：（棵数-1）×间距=路长。当学生建立起两端都栽的植树问题的模型后，两端都不栽、一端栽另一端不栽、封闭曲线植树问题都能根据已有知识进行迁移，从而建立植树问题的数学模型。

五、结语

总而言之，数学核心素养反映数学本质与数学思想，数学课堂培养学生的数学思想并非一蹴而就的事，需要教师潜心教学，用心培养，让数学思想融进课堂，促进学生的发展。