寻幽入微,巧比大小
祁君华


【摘要】比较大小的试题多见于试卷中的中档题或压轴题,除了常用的“中间值法”与“比较法”,本文再归纳总结几个实用的、好用的方法.
【关键词】比大小;方法归纳总结
本文归纳总结几个实用的、好用的方法,助各位莘莘学子攻坚克难,决胜高考.
1特值法
例1若实数a,b,c满足log2a=log3b=4c,则()
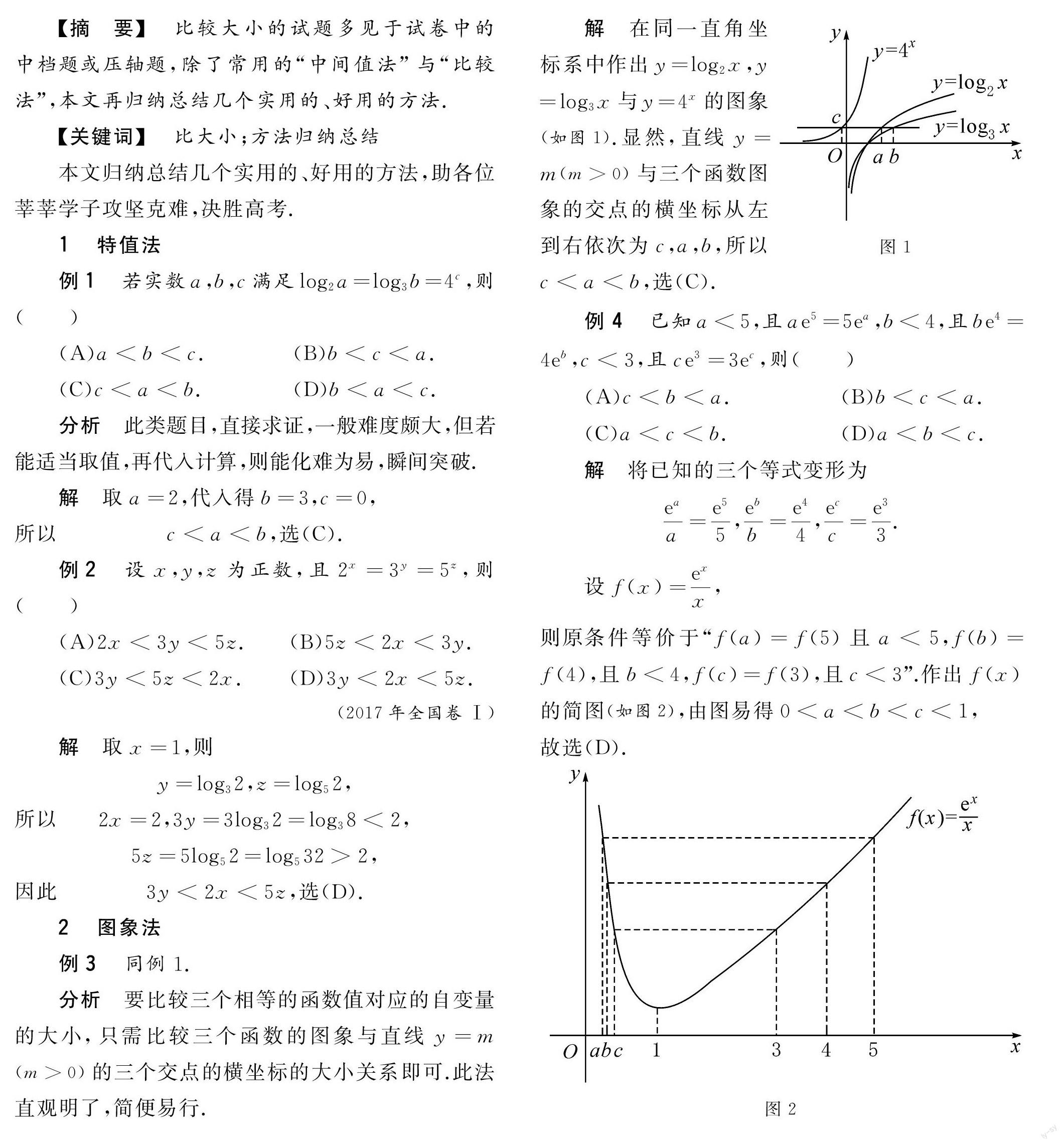
(A)a (C)c 分析此类题目,直接求证,一般难度颇大,但若能适当取值,再代入计算,则能化难为易,瞬间突破. 解取a=2,代入得b=3,c=0, 所以c 例2设x,y,z为正数,且2x=3y=5z,则() (A)2x<3y<5z.(B)5z<2x<3y. (C)3y<5z<2x.(D)3y<2x<5z.(2017年全国卷Ⅰ) 解取x=1,则 y=log32,z=log52, 所以2x=2,3y=3log32=log38<2, 5z=5log52=log532>2, 因此3y<2x<5z,选(D). 2图象法 例3同例1. 分析要比较三个相等的函数值对应的自变量的大小,只需比较三个函数的图象与直线y=m(m>0)的三个交点的横坐标的大小关系即可.此法直观明了,简便易行. 图1 解在同一直角坐标系中作出y=log2x,y=log3x与y=4x的图象(如图1).显然,直线y=m(m>0)与三个函数图象的交点的横坐标从左到右依次为c,a,b,所以c 例4已知a<5,且ae5=5ea,b<4,且be4=4eb,c<3,且ce3=3ec,则() (A)c (C)a 解将已知的三个等式变形为 eaa=e55,ebb=e44,ecc=e33. 设f(x)=exx, 则原条件等价于“f(a)=f(5)且a<5,f(b)=f(4),且b<4,f(c)=f(3),且c<3”.作出f(x)的简图(如图2),由图易得0 故选(D). 图2 3同构法 例5设a=30.5,b=40.4,c=50.3,则() (A)a (C)c 分析乍看之下,三个幂的结构迵然不同(底数不同,指数也不同),不易直接比较.但若细心观察,认真比较,根据分数指数幂的定义,也能将这三个数的结构统一起来. 解a=3510=1035=10243, b=4410=10256,c=5310=10125, 显然c 例6设a=ln43,b=732,c=12ln158,d=0.42.1,则() (A)c>a.(B)b>c.(C)a>b.(D)a>d. 解对于(A), 由于c=12ln158=ln158, 则a=ln43=ln169, 因为158>169, 所以c>a. 对于(B),b=732<14,14=12lne, 而c=12ln22564, 因為22564>e, 所以c>b. 同理a>14, 所以a>b. 又因为d=0.42.1<0.42=0.16, 所以a>d. 故选(A)(C)(D). 4放缩法 例7已知55<84,134<85,设a=log53,b=log85,c=log138,则() (A)a (C)b 分析根据已知条件,易得b<45,c>45,即b 解a-b=log53-log85=log53-1log58 =log53·log58-1log58 所以a 又b 例8已知a=e0.02,b=1.012,c=ln2.02,则() (A)b>c.(B)c>a.(C)a>b.(D)a 分析除了“基本不等式”,常用来放缩的不等式还有ex≥x+1与lnx≤x-1. 解显然a>1,b>1,而c<1. 又lna=0.02,lnb=2ln1.01, 由lnx≤x-1(当且仅当x=1时取等号)可得 ln1.01<0.01, 所以lnb 故选(A)(C). 5构造法 例9设a=2022ln2020,b=2021ln2021,c=2020ln2022,则() (A)a>c>b.(B)c>b>a. (C)b>a>c.(D)a>b>c. 分析仔细观察,灵活变形、转化,可得“a与c的大小关系”等价于“ln20202020与ln20222022的大小关系”.构造函数f(x)=lnxx,利用f(x)的单调性易得f(2020)>f(2022),即a>c.同理可得a与b、b与c的关小关系.(下转第21页)

