傅里叶级数的教学探讨：以信号对称性为例

任蕾 薄华 金欣磊 张韵农

摘要：周期信号的傅里叶级数分析是信号处理类课程的重要教学知识点。文章总结了连续和离散实周期信号的傅里叶级数分析方法，梳理了周期信号的奇偶对称性、奇谐信号和偶谐信号四类情况，对实周期信号傅里叶级数的影响，并通过举例说明其频谱的特征，阐述了连续和离散实周期信号频谱的联系与区别。

关键词：实周期信号；频谱分析；傅里叶级数；离散傅里叶级数；对称性

中图分类号：TP393      文献标识码：A

文章编号：1009-3044（2022）27-0137-05

开放科学（资源服务）标识码（OSID）：

傅里叶级数分析是信号处理类课程的重要知识点，也是课程教学的难点之一。其基本分析工具包括连续傅里叶级数（Fourier series，FS）与离散傅里叶级数（discrete Fourier series，DFS）等。连续周期信号经过傅里叶级数分析得到的频谱是非周期离散谱，若信号具有对称性（本文仅指奇偶对称、奇谐和偶谐信号四类情况），且信号是实信号，则该类信号中仅包含部分频谱分量，利用对称性可简化计算过程，有利于分析连续实周期信号通过线性时不变系统的响应。离散周期序列经离散傅里叶级数分析得到的频谱是周期离散谱，与连续周期信号类似，当离散实周期序列满足某些对称性时，其频谱中也只包含部分频谱分量。建立二者的联系，并通过举例阐述其频谱的特征，有助于该知识点的教学。

国内高校对信号的频谱分析、傅里叶变换的概念及应用的探讨已有相关报道。文献1对离散信号频谱分析的三个基本概念：离散时间傅里叶变换、离散傅里叶变换、离散傅里叶级数进行了总结和辨析[1]。王静等在离散傅里叶变换的讲解中进行了工程实例和理论教学结合的教学实践与探讨[2]。童晓兵等详细探讨了“数字信号处理”课程中共轭对称性，对离散时间傅里叶变换和离散傅里叶变换的共轭对称性进行了对比，列举了该性质在实际工程中的应用[3]。

本文梳理了连续与离散周期信号傅里叶级数分析的一般方法，总结了当信号是实数，且具备奇、偶对称性或信号是奇谐、偶谐信号时，其包含的频谱分量情况，同时给出了相关例题阐述二者的联系与区别。

1 连续与离散周期信号的傅里叶级数

1.1  连续周期信号傅里叶级数分析

根据傅里叶级数[4]的相关理论有：周期为[T]的连续周期信号[ft]的傅里叶级数展开式为：

[ft=n=-∞+∞Fnejnω0t]                        （1）

其中：[Fn=1TTfte-jnω0tdt]               （2）

[ω0=2πT]。

若将[ft]视作其单周期截取后的非周期信号[f0t]经周期延拓构成，即：

[ft=n=-∞+∞f0t-nT]                         （3）

其中：

[f0t=ft，?t∈t0，t0+T0   ，?t?t0，t0+T]                   （4）

且该信号的傅里叶变换（Fourier transform， FT）为：

[f0t?F0jω]                         （5）

则根据连续信号傅里叶变换和傅里叶级数的关系有：

[Fn=1TF0jnω0]                        （6）

因此，连续周期信号的傅里叶级数可以直接利用变换式求解，也可通过式（6）计算获得，该式反映了连续非周期信号的连续谱与连续周期信号频谱之间的联系。

1.2 离散周期序列的傅里叶级数分析

类似地，周期为[N]的离散周期序列[xn]的傅里叶级数展开式[5]为：

[xn=1Nk=0N-1Xkej2πNnk]                  （7）

其中：[Xk=n=0N-1xne-j2πNnk]               （8）

同样，若将[xn]视作其主值区间截取后的非周期序列[xn]经周期延拓构成，即：

[xn=m=-∞+∞xn-mN]                 （9）

其中：

[xn=xnRNn]                     （10）

且該有限长序列的离散时间傅里叶变换（Discrete time Fourier transform，DTFT）为：

[xn?Xejω]                          （11）

则根据离散时间傅里叶变换和离散傅里叶级数的关系有：

[Xk=Xejωω=2πNk]                 （12）

即离散周期序列的傅里叶级数是对离散非周期序列的连续周期谱的采样。

2 信号对称性在实周期信号傅里叶级数分析中的应用

实际应用中，线性时不变系统的激励和响应信号一般为实数信号，同时，实信号的频谱具有幅度谱偶对称、相位谱奇对称的特征。下面我们总结了实周期信号的四类对称性以及在傅里叶级数分析中的一般结论，可用以简化频谱分析，了解实周期信号中所包含的频谱分量，为后续的系统分析奠定基础。

2.1  对称性在连续实周期信号傅里叶级数分析中的应用

当实周期信号[ft]满足某些对称性时，对其进行傅里叶级数展开得到的频谱中只包含某些频率分量。本文我们讨论信号对整周期而言的奇偶对称性以及对半周期而言的奇谐函数和偶谐函数共四类情况。图1示出了连续实周期信号在上述四类对称性情况下傅里叶级数对应的频谱类型。

1）连续实偶周期信号的傅里叶级数

当周期信号[ft]为实偶函数时，其频谱为实偶函数，有[Fn=F?n=F-n]，FS展开式中无正弦项，仅包含余弦项，可能包含直流分量。

证明：由于[ft=f?t]且[ft=f-t]，因此有：

[Fn=1TTfte-jnω0tdt=1T-T2T2fte-jnω0tdt=1T-T2T2ftcosnω0tdt=2T0T2ftcosnω0tdt=F?n=F-n]

2）连续实奇周期信号的傅里叶级数

同理，周期信号[ft]为实奇函数时，其频谱为虚奇函数，有[Fn=-F-n]，FS展开式中无直流分量，也无余弦项，仅包含正弦项。

证明：由于[ft=f?t]且[ft=-f-t]，有：

[Fn=1TTfte-jnω0tdt=1T-T2T2fte-jnω0tdt=-j1T-T2T2ftsinnω0tdt=-j2T0T2ftsinnω0tdt=-F-n]

3）连续、实奇谐信号的傅里叶级数

若周期信号[ft]是实信号，同时满足[ft=-ft±T2]时，称该类信号为奇谐信号，该类信号无直流分量和偶次谐波分量，仅含有奇次谐波分量。

证明：当信号是实信号，且满足平移半周期后奇对称时，有：

[Fn=1TTfte-jnω0tdt=1T0T2fte-jnω0tdt+1TT2Tfte-jnω0tdt=1T0T2fte-jnω0tdt-1TT2Tft-T2e-jnω0tdt=1T0T2fte-jnω0tdt-e-jnπ1T0T2fte-jnω0tdt=0，n=2m2T0T2fte-jnω0tdt，n=2m-1]

需要注意的是，部分连续实周期信号当去除直流分量后才是奇谐信号，在分析时需进行信号去直流的预处理，以方便后续的频谱分析。

4）连续、实偶谐信号的傅里叶级数

同理，实周期信号[ft]满足[ft=ft±T2]时，该信号中无奇次谐波分量，仅含有偶次谐波分量，可能包括直流分量，该类信号称为偶谐信号。

证明：当信号是实信号，且满足平移半周期后重合时，有：

[Fn=1TTfte-jnω0tdt=1T0T2fte-jnω0tdt+1TT2Tfte-jnω0tdt=1T0T2fte-jnω0tdt+1TT2Tft-T2e-jnω0tdt=1T0T2fte-jnω0tdt+e-jnπ1T0T2fte-jnω0tdt=0，n=2m-12T0T2fte-jnω0tdt，n=2m]

偶谐信号本质上周期减半，基波频率是原来的两倍，因此仅含有偶次谐波分量。

2.2 对称性在离散实周期序列傅里叶级数分析中的应用

与连续周期信号类似，离散实周期序列，根据对称性不同，其傅里叶级数对应的频谱也包括四类情况，具体的如图2所示。

1）离散实偶周期序列的傅里叶级数

根据DFS的共轭对称性可得：实偶周期序列的DFS满足：[Xk=X-k=X*-k]，即[Xk]是实偶序列。

2）离散实奇周期序列的傅里叶级数

同理，根据DFS的共轭对称性等有：实奇周期序列的DFS满足：[Xk=-X-k]，且[Xk]是纯虚数序列。进一步，实奇周期序列的DFS展开式中无直流分量。

3）离散实、奇谐序列的傅里叶级数

当离散实周期序列满足[xn=-xn±N2]、且[N]为偶数时称为离散奇谐序列，即该类序列平移半周期后与原序列关于时间轴镜像对称。

此类序列其DFS中仅包含奇次谐波分量，不包含直流分量和偶次谐波分量。

证明：

[Xk=n=0N-1xne-j2πNnk=n=0N2-1xne-j2πNnk+n=N2N-1xne-j2πNnk=n=0N2-1xne-j2πNnk+n=N2N-1-xn-N2e-j2πNnk=n=0N2-1xne-j2πNnk-n=0N2-1xme-j2πNm+N2k=n=0N2-11--1kxne-j2πNnk=n=0N2-12xne-j2πNnk，k=2m-10 ，k=2m]

即此類实周期序列不存在偶次谐波分量，只包含奇次谐波分量。同时，该类序列也不存在直流分量，但有些实周期序列在去除直流分量后可转变为奇谐序列，只要进行如下预处理即可：

[xn-1Nn=0N-1xn=xn-1NX0]     （13）

4）离散实、偶谐序列的傅里叶级数

类似地 ，若离散实周期序列满足[xn=xn±N2]，且[N]为偶数时称为离散偶谐序列，此时序列的实际周期已减半为[N2]。该类序列的DFS中仅包含偶次谐波分量，不包含奇次谐波分量。

证明：

[Xk=n=0N-1xne-j2πNnk=n=0N2-1xne-j2πNnk+n=N2N-1xne-j2πNnk=n=0N2-1xne-j2πNnk+n=N2N-1xn-N2e-j2πNnk=n=0N2-1xne-j2πNnk+m=0N2-1xme-j2πNm+N2k=n=0N2-11+-1kxne-j2πNnk=n=0N2-12xne-j2πNnk，k=2m0 ，k=2m-1]

即此类序列不存在奇次谐波分量，只有偶次谐波分量，原因是此时周期序列其实际的基波频率是原来的两倍导致不可能存在奇数次谐波分量。

通过上述总结可见，连续和离散周期信号的傅里叶级数有相似的性质。它们的主要差别在于离散序列的频谱是周期谱，这是由于时域中连续信号采样导致的。

3 举例与分析

为验证上述实周期信号的对称性和傅里叶级数的相关结论，我们分别举例说明。并对比连续和离散信号的傅里叶级数，阐述二者的联系与区别。

3.1  连续实周期信号的FS分析举例

在下列例题中我们首先定义脉冲信号：

[Gτt=ut+τ2-ut-τ2]     （14）

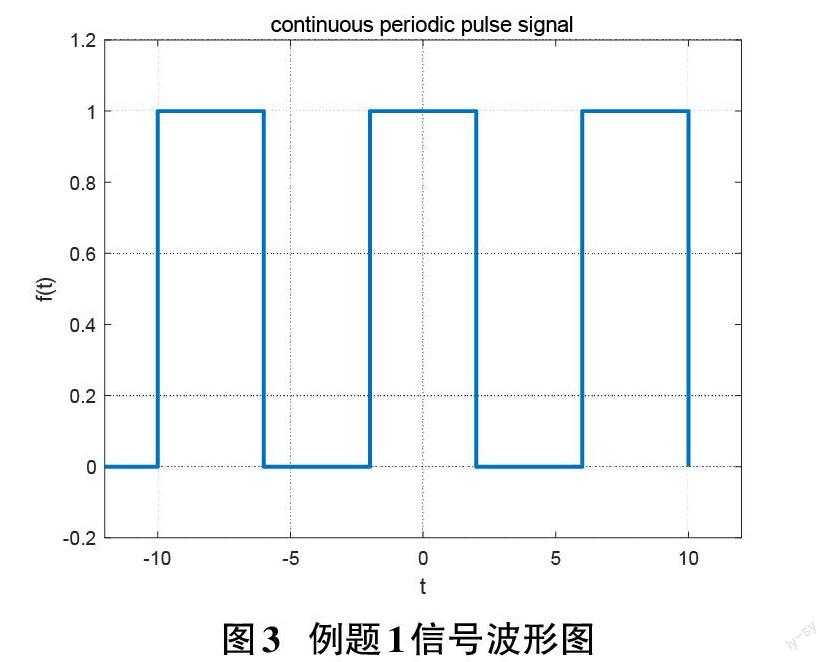
例题１：已知如图3所示的连续实周期信号：[ft=n=-∞+∞G4t-8n]，求其傅里叶级数。

解：该信号是实偶连续周期信号，同时去除直流分量后也是奇谐信号，故其FS是实偶信号，且仅包含奇次谐波余弦项和直流分量。利用公式（6）有：

[G4t?4Sa2ωFn=1TF0jnω0=18×4Sa2n×2π8=12Saπn2]

因此该信号的FS展开式为：

[ft=n=-∞+∞12Saπn2ejnπ4t=12+n=1+∞Saπn2cosnπ4t]

其FS的幅度谱如图4所示，其中红色曲线是信号[G4t]的连续谱，可见周期信号[ft]的FS频谱是对其的采样，而本信号中仅包含直流和奇次谐波分量。

例题2：已知如图5所示的连续实周期信号：[ft=n=-∞+∞ut+2-4n-2ut-4n+ut-2-4n]，求其傅里叶级数。

解：该信号是实奇信号，同时也是奇谐信号，因此其FS中仅包含奇次谐波正弦项、无直流分量，且其FS是纯虚信号（注：该题解法不唯一，此处仅考虑对称性的应用）。利用公式（6）有：

[ut+2-2ut+ut-2?2Saω×2jsinωFn=1TF0jnω0=14×4jSan×2π4sinn×2π4=jSaπn2sinπn2]

因此该信号的FS展开式为：

[ft=n=-∞+∞jSaπn2sinπn2ejnπ2t=2jn=1+∞Saπn2sinπn2sinnπ2t]

其FS的幅度谱如图6所示，其中红色曲线是信号[ut+2-2ut+ut-2]的幅度譜，可见周期信号[ft]的FS频谱是对其的采样，而本信号中仅包含奇次谐波分量。

3.2  离散实周期序列的DFS分析举例

例题3：已知如图7所示的离散实周期序列：[xn=m=-∞+∞R5n+2-9m]，求其离散傅里叶级数。

解：该离散实周期序列是偶对称序列，因此根据前述结论可得：该序列的DFS是实偶信号。利用公式（11）（12）有：

[R5n+2?sin52ωsinω2Xk=Xejωω=2πNk=sin52×2π9ksin12×2π9k=sin5π9ksinπ9k]

[xn=19k=08sin5π9ksinπ9kej2π9nk]

其DFS的幅度谱如图8所示，其中红色曲线是非周期序列[R5n+2]的连续周期幅度谱，可见周期序列[xn]的DFS频谱是对前者的采样，且是实偶频谱。

例题4：已知如图9所示的离散实周期序列：[xn=m=-∞+∞R4n-8m]，求其离散傅里叶级数。

解：该离散实周期序列的直流分量为0.5，去除后的序列是奇谐信号，因此根据前述结论可得：该序列的DFS中只有奇次谐波分量和直流分量。利用公式（11）（12）有：

[xn=18k=07e-j38πksinπ2ksinπ8kej2π8nk]

其DFS的幅度谱如图10所示，其中红色曲线是非周期序列[R4n]的连续周期幅度谱，可见周期序列[xn]的DFS频谱是对前者的采样，本序列仅包含直流分量和奇次谐波分量。

4 结束语

总结并梳理了实周期信号的傅里叶级数分析中，信号对称性导致的一般性结论，本文讨论了信号的奇偶对称性和奇谐信号、偶谐信号四类情况。应用上述对称性可以在傅里叶级数分析中简化运算，为后续分析周期信号通过线性时不变系统提供基础。此外，我们还对比了连续和离散周期信号傅里叶级数的联系和区别。

参考文献：

[1] 周剑雄，石志广，吴京.离散时间信号频域分析中的概念辨析[J].电气电子教学学报，2014，36（1）：49-51.

[2] 王静，杨玲君，刘开培.基于工程实例的DFT教学实践与探索[J].电气电子教学学报，2021，43（1）：69-72.

[3] 童晓兵，徐以涛，张玉明.“数字信号处理”课程中共轭对称性的探讨[J].电气电子教学学报，2014，36（3）：19-21.

[4] A.V.奥本海姆. 离散时间信号处理（第2版）[M]. 北京：电子工业出版社，2011.

[5] 程佩青.数字信号处理教程Matlab版[M].5版.北京：清华大学出版社，2017.

【通联编辑：王力】