CPFS结构理论下的全概率公式教学研究

马杰 李多猛

摘  要：喻平教授通过多年的教学实践，建构了以概念域、概念系、命题域、命题系为核心的CPFS结构理论. 文章借助CPFS结构理论，多维度诠释全概率公式，从理想化的古典概型到一般化的全概率，从将加权平均类比到全概率公式，从借助韦恩图到直观理解全概率，让学生厘清概率知识之间的逻辑关联，形成概念体系，培养学生的数学核心素养.

关键词：CPFS结构理论；全概率公式；数学核心素养

一、引言

概念是反映对象本质属性的思维形式. 数学概念是组成数学知识的最基本的构成单位，是判断命题真假的重要依据之一. 对于数学概念的学习，南京师范大学的喻平教授提出了CPFS结构理论，其中C，P，F，S分别是概念（concept）、命题（proposition）、域（field）、系（system）的英文首字母的缩写，该理论由概念域、概念系、命题域、命题系构成，是一种在学习中体现数学思维特点的个体认知结构. CPFS结构理论从多角度诠释了概念的等价表述，让学生在头脑中形成概念域；明示多个概念之间的关系，建立概念网络，从而形成概念系. 命题域是指满足某种关系的公理、定理、公式、法则等组合而成知识体系；通过对知识的训练巩固，学生在头脑中能根据一组命题推出其他命题，从而形成命题系. 如果学生不能全方位、多背景地深入了解概念，没有在头脑中形成概念系或命题系，一旦换一个侧面或角度阐述同一个概念或命题，他们就会不知所云. 因此，笔者基于CPFS结构理论设计“全概率公式”的教学，通过设置系列问题，建立概念网络，循序渐进地直观呈现各种相关概念之间的联系，帮助学生构建良好的知识网络体系，培养学生的数学抽象和逻辑推理素养.

二、教材分析

“全概率公式”是北师大版《普通高中教科书·数学》选择性必修第一册第六章“概率”第一节“随机事件的条件概率”第三课时的教学内容，前两课时分别为“条件概率”和“乘法公式与事件的独立性”. 对于概率的学习，《普通高中数学课程标准（2017年版2020年修订）》指出，要帮助学生结合具体案例，理解样本点、有限样本空间、随机事件，会计算古典概型中简单随机事件的概率，加深对随机现象的认识和理解. 对本单元的学习要求是“帮助学生了解条件概率及其独立性的关系，结合古典概型，会利用全概率公式计算概率”. 显然，古典概型是后续概率知识学习的基础，条件概率、概率的加法公式和乘法公式、全概率公式等知识具有较强的联结性，最终都应用于求实际生活中事件的概率. 通过全概率公式的教学，可以培养学生数据分析、数学建模、数学抽象和数学运算等素养.

三、学情分析

对于学生来说，古典概型属于一种理想化的概率模型，有固定的解决问题程序，易于掌握. 但对于条件概率，学生既要明确[PAB]和[PBA]的区别和联系，又要辨析互斥事件、相互独立事件，还要灵活运用[PBA=PABPA]和[PBA=nABnA]两个公式. 显然，条件概率在理解和应用上要难于古典概型. 而全概率公式的教学又建立在古典概型和条件概率的基础之上，还要使用互斥事件的概率加法公式和条件概率的乘法公式. 因此，多个知识点的交会，对学生来讲，无疑增加了学习的难度.

四、教学过程

1. 呈现背景，分析例题

例1  有三个箱子，分别编号为1，2，3. 1号箱中装有1个红球和4个白球，2号箱中装有2个红球和3个白球，3号箱中装有3个红球. 这些球除颜色外完全相同，某人先从三个箱子中任取一箱，再从中任意摸出一球，求取得红球的概率.

设置问题：（1）假设事件A表示“取得红球”，事件Bi表示“球取自i号箱”（i = 1，2，3）. 那么，如何用符号语言表示红球来自1号箱、2号箱或3号箱？

（2）事件B1，B2，B3之间是什么关系？

（3）事件A的发生和事件Bi（i = 1，2，3）之间有什么关系？你能用概率的符号语言表示这种关系吗？你能利用概率的加法公式和概率的乘法公式求出[PA]吗？

【设计意图】让学生把互斥事件，以及概率的加法公式、乘法公式等知识串联起来，进而转换、应用到题目的求解中. 通过这种“不捅破窗户纸”的问题串，让学生认识到概率知识间的关联作用，以便顺利展开对全概率公式的教学，同时体现了知识循环上升的过程.

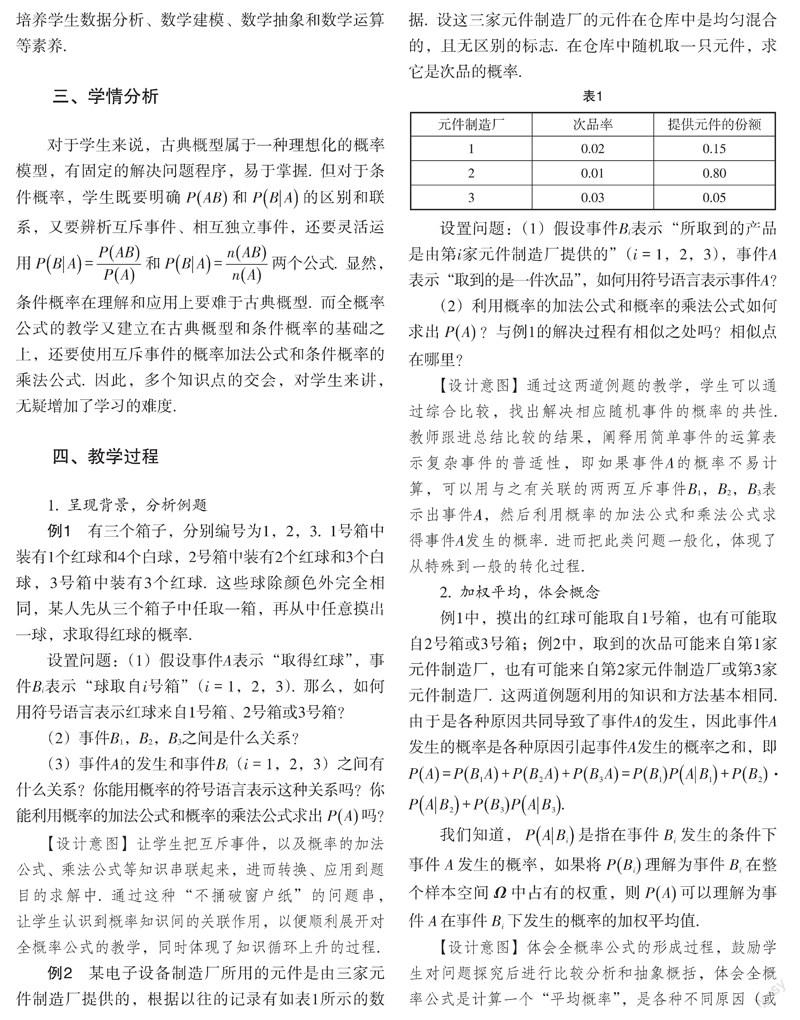
例2  某电子设备制造厂所用的元件是由三家元件制造厂提供的，根据以往的记录有如表1所示的数据. 设这三家元件制造厂的元件在仓库中是均匀混合的，且无区别的标志. 在仓库中随机取一只元件，求它是次品的概率.

设置问题：（1）假设事件Bi表示“所取到的产品是由第i家元件制造厂提供的”（i = 1，2，3），事件A表示“取到的是一件次品”，如何用符号语言表示事件A？

（2）利用概率的加法公式和概率的乘法公式如何求出[PA]？与例1的解决过程有相似之处吗？相似点在哪里？

【设计意图】通过这两道例题的教学，学生可以通过综合比较，找出解决相应随机事件的概率的共性. 教师跟进总结比较的结果，阐释用简单事件的运算表示复杂事件的普适性，即如果事件A的概率不易计算，可以用与之有关联的两两互斥事件B1，B2，B3表示出事件A，然后利用概率的加法公式和乘法公式求得事件A发生的概率. 进而把此类问题一般化，体现了从特殊到一般的转化过程.

2. 加權平均，体会概念

例1中，摸出的红球可能取自1号箱，也有可能取自2号箱或3号箱；例2中，取到的次品可能来自第1家元件制造厂，也有可能来自第2家元件制造厂或第3家元件制造厂. 这两道例题利用的知识和方法基本相同. 由于是各种原因共同导致了事件A的发生，因此事件A发生的概率是各种原因引起事件A发生的概率之和，即[PA=PB1A+ PB2A+ PB3A=PB1PAB1+ PB2 ·][PAB2+PB3PAB3.]

我们知道，[PABi]是指在事件[Bi]发生的条件下事件[A]发生的概率，如果将[PBi]理解为事件[Bi]在整个样本空间[Ω]中占有的权重，则[PA]可以理解为事件[A]在事件[Bi]下发生的概率的加权平均值.

【设计意图】体会全概率公式的形成过程，鼓励学生对问题探究后进行比较分析和抽象概括，体会全概率公式是计算一个“平均概率”，是各种不同原因（或条件）下某事件发生的条件概率的加权平均，各原因出现的概率不同，因此各条件概率的权重也不同.

3. 归纳总结，抽象概括

事件[A]发生有各种可能的原因[Bi i=1，2，3，…，n，] 且各原因彼此互斥并涵盖所有可能的情形（即各原因之和构成了样本空间）. 若事件[A]的发生是由原因[Bi]引起的，则事件[A]发生的概率是[PABi=PBiPABi.] 由于每个原因都可能导致事件[A]的发生，故事件[A]发生的概率是各原因引起事件[A]发生的概率的和，即[PA=i=1nPBiPABi.]

【设计意图】帮助学生厘清全概率公式的本质就是综合运用概率的加法公式和乘法公式解决“多因一果”的概率问题，引导学生充分体会“多因一果”的概率问题的本质就是将一个复杂事件的概率问题转化为不同条件（原因）下发生的简单事件的概率求和问题，帮助学生学会寻找导致复杂事件发生的原因，并厘清各原因之间的关系. 深入理解全概率公式的内涵，充分体会全概率公式的形成过程.

4. 借助Venn图，形成概念域

设置问题：如图1，从集合的角度看，分别表示交事件（或积事件）、并事件（或和事件）、互斥事件. 在条件概率的学习中，用图2表示事件[B]发生的条件下事件[A]发生的概率. 那么，如何利用Venn图表示例1和例2中的事件之间的关系呢？

【设计意图】利用知识的正向迁移，让学生自己根据所学知识，借助Venn图构建全概率公式的直观形式（如图3），提升学生的直观想象能力，增强学生的概念理解力，进而形成全概率的概念域.

5. 理性分析，强化应用

练习1：采购员要购买一包某种电器元件（一包中有10个）. 他的采购方案是：从一包电器元件中随机抽查3个，如果这3个电器元件都是好的他才买下这一包电器元件. 假定每包中含有4个次品电器元件的包数占30%，而其余每包电器元件中各含有1个次品，求采购员随机挑选一包电器元件后拒绝购买的概率.

解析：因为采购员可能取到含有4个次品的一包电器元件，也可能取到含有1个次品的一包电器元件，所以可以设[B1]表示事件“取到含有4个次品的一包电器元件”，[B2]表示事件“取到含有1个次品的一包电器元件”，[A]表示事件“采购员拒绝购买”. 则事件[B1，B2]构成样本空间的一个划分. 由题意，知[PB1=310，PB2=710.]

结合古典概型的概率计算公式，得

[PAB1=1-C36C310=56，PAB2=1-C39C310=310.]

故由全概率公式，得

[PA=PB1PAB1+PB2PAB2=310×56+710×]

[310=2350.]

所以采购员随机挑选一包这种电器元件后拒绝购买的概率为[2350.]

练习2：甲、乙、丙三人同时对飞机进行射击，三人击中的概率分别为0.4，0.5，0.7. 飞机被一人击中且击落的概率为0.2，被两人击中且击落的概率为0.6，若三人都击中，飞机必定被击落，求飞机被击落的概率.

解析：由题意知，飞机被击落与被几个人击中有关. 因此，可设[A]表示飞机被击落；[Bi]表示事件“飞机被[i]个人击中”（[i=0，1，2，3]），则事件[B0，B1，][B2，B3]是构成样本空间的一个划分.

由题意，知[PAB0=0，PAB1=0.2，PAB2=0.6，][PAB3=1.]

设[Hi]表示事件“飞机被第[i]个人击中”（[i=1，][2，3]），

则事件[Hi]彼此相互独立，且

[PB1=PH1H2H3?H1H2H3?H1H2H3=PH1H2H3+]

[PH1H2H3+PH1H2H3=0.4×0.5×0.3+0.6×0.5×0.3+][0.6×0.5×0.7=0.36.]

同理，[PB2=PH1H2H3?H1H2H3?H1H2H3=0.41，]

[PB3=PH1H2H3=0.14，PB0=PH1H2H3=0.09.]

由全概率公式，知

[PA=PB0PAB0+PB1PAB1+PB2PAB2+]

[PB3PAB3=0.09×0+0.36×0.2+0.41×0.6+0.14×1=0.458.]

所以飞机被击落的概率是[0.458.]

【设计意图】通过习题教学示范解题步骤，帮助学生深化对公式的理解和掌握，促使学生能准确运用公式解决实际问题. 同时，引导学生归纳、总结运用全概率公式的一般步骤，全面提升学生对全概率公式的认知和理解.

6. 归纳总结，形成概念系

全概率公式的学习是以古典概型、条件概率的乘法公式、互斥事件的概率加法公式等作为知识基础的. 因此，要整合之前所学的概率知识，让学生从大单元视角明确全概率公式的地位，建立整个概率知识网络框架（如图4），为后续统计知识的学习提供理论基础.

五、教学启示

概率是衡量随机事件发生可能性大小的工具，是从不确定性的角度认识现实世界的思維模式和解决问题的方法. 拉普拉斯曾说，生活中的重要问题，其中绝大多数在实质上只是概率问题. 研究概率问题就要研究随机事件，研究样本点之间的关系. 从知识的发展角度来看，全概率公式建立在古典概型、互斥事件的加法公式、条件概率、概率乘法公式等知识的基础上，可以解决生活中更一般性的概率问题. CPFS结构理论有利于构建全概率知识网络，进而形成概念域和概念系.

在当今社会背景下，科技竞争日趋激烈，近几年众多高校都新增了人工智能、智能感知工程、数据科学与大数据技术等专业. 其中，人工智能原理的背后就有全概率公式、贝叶斯公式所体现的思想. 章建跃博士认为，基于统计与概率的实践品质和应用取向对培养学生的实践能力和用数据说话的理性精神是其他学科无法替代的. 全概率公式的实质就是利用简单事件的运算表示复杂事件，它丰富、完善了概率的运算法则，为求一类复杂事件的概率提供了有力的工具，体现了化难为易的转化思想，加深了学生对不确定现象的认识. 因此，全概率内容的学习既能让学生体会概率教学中的随机思想，还可以培养学生数学建模、数学抽象、逻辑推理和数学运算等素养.

参考文献：

［1］南开大学哲学系逻辑学教研室. 逻辑学基础教程［M］. 天津：南开大学出版社，2014.

［2］傅赢芳，喻平. CPFS结构理论及其对数学概念教学的启示［J］. 教育研究与评论（中学教育教学），2020（6）：28-33.

［3］中华人民共和国教育部制定. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［4］章建跃. 核心素养立意的高中数学课程教材教法研究［M］. 上海：华东师范大学出版社，2021.

收稿日期：2022-09-11

作者简介：马杰（1973— ），男，中学高级教师，主要从事数学教学研究.