美国《加利福尼亚州公立学校数学框架·教学》修订草案简介与启示

摘  要：美国《加利福尼亚州公立学校数学框架》已经启动新一轮的修订工作，草案中重点突出了“公平”和“参与”两个关键词，在大量研究与实践的基础上，针对数学教学进行了深刻地阐述，其认识和见解值得学习与借鉴. 文章除了重点介绍草案中有关教学的新颖之处，还提出相关启示与思考.

关键词：《加利福尼亚州公立学校数学框架》；数学教学；教师专业学习

一、引言

教学一直是数学教育关注的重点环节. 一个好的教学过程可以充分发挥教师的主导作用，让学生真正参与到“做数学”的过程中，最终实现教学目标. 教学是一门艺术，需要教育工作者在不断实践中积累经验. 与此同时，如果教师能够积极汲取先进的教育理念、教学策略和教学方式，并将其合理融入实际教学中，就能为教学改革、教师专业发展创造新的机会.

他山之石，可以攻玉. 辩证看待美国数学改革前沿是提高我国数学教育质量的有效途径之一. 美国加利福尼亚州从2013年起采用《加利福尼亚州公立学校数学框架》（Mathematics Framework for California Public Schools）（以下简称《数学框架》），代替了《加利福尼亚州共同核心数学标准》（California Common Core State Standards for Mathematics，CA CCSSM），使之能够更好地指导课程开发与教学. 很多研究者对《数学框架》中的重要内容，如评价、技术、教学策略等进行了不同的研究. 在实施该版《数学框架》近6年后，加利福尼亚州教育局、教学质量委员会和州教育委员会于2019年开始着手对其进行修订.《数学框架》的修订草案在2021年1月获得教育质量委员会的批准，并在加利福尼亚州教育部官方网站进行公示，以供大众审查和评论，旨在给对《数学框架》修订工作感兴趣的个人或者组织提供发表建议的机会. 2021年5月中旬，教育质量委员会对收到的评论与建议进行审核，并于2021年6 ～ 7月对《数学框架》修订草案进行第二次公开审核. 本次《数学框架》进行修订的目标是让所有加利福尼亚州学生成为数学的有力使用者，以便他们在大学学习、职业生涯和公民生活中更好地了解和积极影响世界.《数学框架》（修订版）的不同之处是单独设置了新的一章——公平与参与的教学，其目的是促进教学，为所有人创造公平的学习体验，挑战导致不公平结果的根深蒂固的政策和做法. 同时，修订草案的第九章还给出了实现这种教学愿景的相关支持. 基于此，本文主要介绍《数学框架》修订草案中与教学密切相关的内容（以下统称《数学框架·教学》）. 从中挖掘新一轮修订中有关教学的建议与理念，把握改革的新动向与新趋势，为我国数学课程标准的实施与完善提供一些参考和启示.

二、简介

1. 公平与参与的教学

我国《普通高中数学课程标准（2017年版2020年修订）》提出了“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”的课程理念，并在教学建议中强调“不仅要重视教，更要重视学”，倡导教育公平，重视学生参与. 公平和参与成了本次《数学框架》新一轮修订的两个关键词，并强调好的教学方式能带来公平和更好的结果. 教学与公平共同创造了能够带来公平结果的教学设计. 州一级对公平的承诺贯穿整个《数学框架》修订草案，并且其中的每一章都阐述了帮助数学教育工作者为所有人创造和维持公平机会的考虑因素和方法.

强调公平是因为关注到多年来数学的发展把许多学生排除在外的事实.《数学框架·教学》指出，加利福尼亚州的所有教师都要努力确保每个孩子有平等的机会获得成功. 数学教师要提供公平的教育，确保所有的学生得到关注、尊重和资源. 因为加利福尼亚州的课堂结合了不同的社区和学生，文化和语言资源更复杂，所以教师要立足这种现状，利用这些资源创建与文化相关的课程. 总之，教育工作者必须确保为加利福尼亚州所有学生提供学习支持.

重视参与是因为学生通过积极参与教学和相互学习能获得最佳学习效果. 因此，《数学框架·教学》确定了开展探究学习的三个探究驱动因素（Drivers of Investigation，DI）：了解世界（Make sense of the world）；预测可能发生的事情（Predict what could happen）；影响未来（Impact the future）. 探究驱动因素揭示了为什么学习数学，并与四类内容连接（Content Connections，CCs）配对，它揭示了在活动中应该如何学习及学习怎样的数学. 与数学实践的标准（Standards for Mathematical Practice，SMP）一起，探究驱动因素通过连贯、集中和嚴谨的方式促进学生对内容连接中思想和行动的学习. 教师合理使用探究驱动因素能够激发学生的好奇心，并为他们深入学习真实的数学提供动力. 实际上，当学生参与到各种各样的体验中时，他们可以更积极地看待数学及自身与数学的关系. 除此之外，《数学框架·教学》还给出了通用学习设计（Universal Design for Learning，UDL）指南的原则，包括提供多种参与方式、多种表现方式、多种行动方式和多种表达方式. UDL是全纳教育（inclusive education）的具体写照，关注到学生学习的差异性，以此为所有学生提供有利于他们学习的多维指南.

2. 公平与参与教学的组成部分

教师应该如何创造一个公平和参与的数学学习环境以支持所有学生的数学学习？《数学框架·教学》在相关研究和实践的基础上回答了这个问题，并提出了公平与参与教学的五个重要组成部分. 这五个部分既相互独立，又相互支持、相互影响，共同促进教学迈向公平，深化学生参与数学学习的深度与广度.

（1）围绕大概念设计教学（Plan Teaching Around Big Ideas）.

数学是一门由重要的思想和联系组成的学科，理解数学的大概念具有重要意义.《数学框架·教学》提出，大概念是指那些能够反映学生所处年级的数学课程特点，以及知识之间关系的概念，是数学学习的核心，可以将众多数学理解联系成一个连贯的整体，并为学生的探究提供活动中心. 围绕大概念进行教学设计，实际是提出了一种对数学教学内容进行处理的方式，这与以往的课程标准倾向于将学科划分为更小的主题的方式不同. 教师可以计划教授数学的大概念，而不是围绕标准或教材章节中规定的小主题或方法进行教学. 围绕大概念设计的课程有助于将一个或多个内容与数学实践标准和探究驱动因素联系起来.《数学框架·教学》认为，在讨论学习重要数学概念的新方法时，教师应该以问题为引导，提供给学生充足的时间去思考问题的解决方案，之后再引导学生获得相应的方法和策略，以找到教师指导的最佳时机.

《数学框架·教学》中举了这样一个例子：高中几何教师Lori向学生提出了一个问题：一位农民有36个单独的栅栏，每个栅栏长一米，农民想把它们放在一起，围成尽可能大的面积. 这个问题在我们的教学中其实是一个很常见的现实情境问题，但是Lori不仅花时间延拓了学生的农业知识，以及加利福尼亚州在水果、蔬菜和牲畜生产中的作用，而且组织学生积极讨论农场和农民想要栅栏形成某种形状的原因. 另外，Lori在黑板上尽可能地张贴出所有规则和不规则图形的图片，贴上标签，还给出了一个句子框架“栅栏应布置成（    ）形状，因为（    ）”来帮助学生思考. 经过一番讨论后，Lori要求学生考虑栅栏可能形成的最大区域. 一些学生从调查不同大小的矩形和正方形开始，一些学生绘制图表来调查不同边长图形的面积如何变化. 案例中还指出一位学生想要围成一个三十六边形，从而需要用到三角学的知识. 在探究这个问题的过程中，学生可以重新审视自己已有的知识，并且将这些知识统筹在“面积”这一大概念之下. 这与我国现在数学教学中提倡的单元式教学中强调的核心概念不谋而合.

（2）使用开放的、引人入胜的任务（Use Open，Engaging Task）.

在教学中选择开放式的任务或问题是实现学生参与的有效方式. 开放式任务是指能让学生将想法发展到不同水平的任务. 当任务既有一个较低的要求，又有一个高的标准，则意味着任何学生都可以尝试对任务进行解决，并逐步向高水平任务靠近. 当问题较为封闭时，只有一些学生在适当的水平上受到认知上的挑战，而且问题往往并不有趣. 如果任务是开放的，这类问题就能在学生的知识与能力范围内给予所有学生适当的挑战. 开放式任务可以源于现实世界，以帮助学生积累将与之生活息息相关的情境数学化的体验. 例如，可以让学生设计轮椅坡道、规划新的学校花园等. 这类从生活中提取的任务与想象中的情境是截然不同的. 但是，现有的教材中却充斥着大量想象的情境. 同时，并非所有的数学问题都需要与现实相关，学生也可以充分参与到纯数字模式的问题探索中去.

一方面，学生在探究开放式任务时，能利用各种真实机会以不同的方式参与其中，以不同的方式看待问题，使用多种方式来表征数学思想和表达理解，贡献自己独特的观点. 这有助于学生进行概念理解和推理，以及平等地参与数学对话；另一方面，开放式任务为教师创造了倾听、理解学生想法的机会，并在课程实施过程中进行形成性评估.

《数学框架·教学》中举了两个开放性的问题范例. ① 你能用四个4以及加、减、乘、除等运算符号（可以进行添加括号等任何操作）找到1到20之间的每个数字吗？例如，[4+4÷4+4=6，] 结果6属于1到20之间，符合要求. 这样的问题不仅可以发散学生的思维，而且提高了数学的趣味性. ② 谁在你们学校上学？哪些种族和性别群体有代表性？你的学校数据与州或国家数据相比如何？这个问题与我们日常教学中所设置的有关统计和概率知识的问题相比较，内涵更丰富，更贴近学生的生活，还能进一步发展学生的数学建模素养.

使用开放式任务代表着教学实践的转变，其不再是传统的“讲座”方式. 强调在教学中合理安排开放式任务，促使教师通过丰富的、真实的、与文化相关的任务来引领学生探究数学知识，这将支持学生的持续成长，并丰富他们的学习经验，而这正是消除不公平现象的一个基本要素.

（3）教学走向社会正义（Teach Toward Social Justice）.

真正的数学教学应该是面向社会正义的. 数学教师有必要向学生灌输这样一种观点，即数学是一种既可以用来理解世界，又可以用来改变世界的工具. 《数学框架·教学》指出，传统意义上，数学被视为一门中立的学科，它阻碍了学生与数学建立更为私人和紧密关系的可能，并导致很多学生认为他们不适合学习数学. 从不同的角度来看，教师不仅可以帮助学生从数学中看到自己，还可以积累知识和促进理解，使他们能够利用数学来改善世界. 教师可以在任何年级（幼儿园至十二年级）采取以公正為导向的观点，帮助学生感受归属感，并为他们提供解决生活和社区中重要问题的工具. 同时，因为不同的学生有着不同的背景、经历和文化身份，所以教师应该赋予数学多元文化的背景. 例如，设计的数学项目侧重于将获得水作为一项人权，其中就整合了体积、容量、操作和比例推理等主题，以探讨发展中国家家庭用水和获得水的情况. 或者在一堂关于在美制和公制之间单位换算的测量课中，让学生借助自己家庭的移民经历，在经历了地图探索和一系列讨论后，运用并拓展数学技能.

数学教学中，要采取社会公正的方法使数学更人性化. 学习不仅可以获取新知识，还涉及身份的改变. 若将所有学生定位为数学思考者、学习者和社区成员，学生则能在此过程中将数学视为与他们的生活相关的东西. 教学中设计的任务不仅是为了让学生参与有意义的数学，有时也是为了帮助学生注意到自己已经是数学学习活动的重要成员，加强学生数学学习的主人翁意识. 教学走向社会正义需要教育工作者为学生提供必要的支持，教师要通过任务帮助学生用数学阅读和认识世界，即用数学解读世界；然后学习用数学改变世界，即用数学书写世界. 这恰好与我国《义务教育数学课程标准（2022年版）》中提出的核心素养三大构成方面有异曲同工之处.

（4）鼓励学生提问和猜想（Invite Student Questions and Conjectures）.

维持学生对数学的好奇心是教学的任务之一. 从数学中的大概念出发设置的开放式任务可以培养学生的好奇心. 教师也可以为学生营造提问和猜想的空间来激发学生的学习兴趣. 事实上，课堂上最重要但被忽视的数学行为之一便是引导学生提出数学问题. 这样的问题是宝贵的教学资源，对于培养活跃、好奇的数学思考者很重要，应该受到重视，并给予学生时间去探究. 当学生对数学有了好奇心后，借助开放式任务进行大概念的探索，并为另一个重要的数学行为——猜想做充分的准备. 假设是一种需要检验和证明的想法，而假设在数学学科的等价物就是猜想. 鼓励学生提出关于数学的猜想，并对猜想进行讨论和探究，会让其意识到数学是一门可以借助逻辑进行深入探索的学科. 好奇心和判断力正是通过猜想得到了培养，而这与探究驱动因素紧密相关.

（5）以推理和论证为中心（Center Reasoning and Justification）.

推理是做数学和学数学的核心，数学教学应该紧紧围绕推理和论证展开. 《数学框架·教学》认为，所有的学生都能对数学进行深刻地思考. 数学推理支持并改善了日常生活而应备受重视. 一个学会对自己的想法进行推理的学生，就是要学会成为数学的优秀传播者. 在实际教学中，教师要向学生分配开放式任务，引导学生切身参与到数学推理的过程中，并要求其相互讨论想法和理由. 在经历全班讨论和小组讨论探究数学问题的过程中，有效促进学生推理能力的发展. 因此，以推理和论证为中心成为开放式任务的核心要义，需要依托开放式任务展开. 例如，学生可能会注意到多边形的内角和会随着边数的增加而有规律地增加，并使用这种重复推理来推测任何多边形内角和的规律，教师则需要充分利用这类问题来发展学生的推理和论证能力. 换言之，在教学过程中，教师要深度挖掘蕴藏着数学推理和论证的问题，用更加清晰的方式提出问题，有意识、有目标、有评价地助力学生能力的提升.

《数学框架·教学》对推理和论证的重视不仅源于数学本身的特质，还源于社会发展的迫切需求，即数学推理是21世纪就业的必备技能. 雇主过去高度重视那些能够计算并给出正确答案的人，但现在计算机执行计算，需要雇员编写计算机程序，理解解决方案，推理数学路径，并交流他们的想法，以便其他团队成员与他们联系. 与快速计算相比，灵活和创造性思维在当今职场中更受重视.

3. 公平、参与的数学教学的有效支持

基于上述五种理念，《数学框架·教学》中还阐述了如何为创造公平与参与的教学提供相应的具体支持，旨在为教师建立一个有效的支持系统. 正因为教师是影响学生学习的重要因素之一，所以关注教师就有重要的意义.

《数学框架·教学》给出了适合所有年级公平教学的大致轮廓，如表1所示. 五个步骤逻辑清晰、步步深入，公平与参与既是教学的起点，又是教学力争达到的目标.

对教师而言，改进自己教学的途径非常多. 例如，在课堂中与学生合作、参与会议和参加线上课程等. 但是《数学框架·教学》更关注教师的专业学习. 专业学习指的是有计划和有组织的过程，通过使用数据、围绕真实问题和教学实践的主动探究，促进教育者的可持续发展. 与之相关的概念——有效的专业发展，指的是结构化的专业学习，这种学习能带来教师实践的改变和学生学习结果的改善.

“理念先行，行动跟进”是促进教师专业发展的重要策略之一，而教师的专业发展是改善教学的有效抓手.《数学框架·教学》总结了有助于改进教学实践的专业学习思维的关键转变，为教师教学理念的革新提供指导，详见表2. 从转变中可以明确感受到，教师专业发展是一个持续的过程，紧密围绕学生、教学和教师本人三大着力点展开. 教师专业学习的主体性意识越强，越能在发展过程中获得各方面的坚实保障.

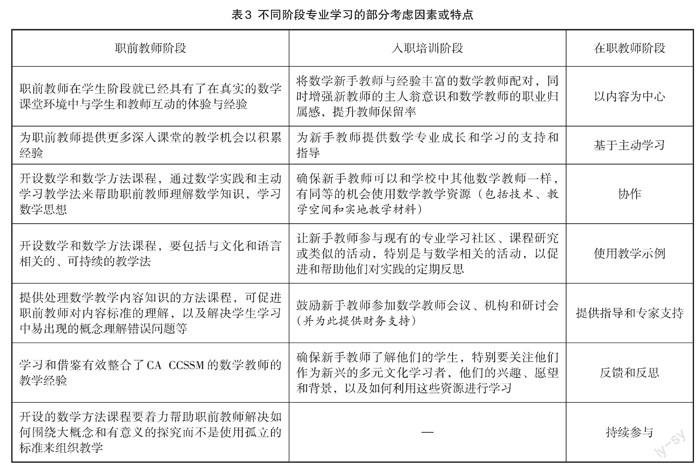
在此基础上，《数学框架·教学》还分析了数学教师职业生涯不同阶段的专业学习，包括职前教师阶段、入职培训阶段和在职教师阶段，并给出了不同阶段专业学习的特点或应该考虑的因素，如表3所示. 这些内容共同构成了连贯、完整的教师发展成长体系，且各有侧重，并以增强数学教学的公平性与参与性为目标，致力于帮助学生实现数学上的成就，实现教育教学质量的提高. 最后，《数学框架·教学》还给出了有效专业学习的三种方式：课程研究，以内容为中心的研讨会，结构化辅导.

三、启示

1. 立足本国国情，妥善处理公平与成效间的关系

一直以来，教育公平都是各个国家关注的重点议题. 导致美国数学教育不公平的因素很多，如移民特性所导致的种族、语言差异，而更深层次的是文化差异. 数学本身就是一种文化，从文化角度出发，我国也存在地域文化差异. 若从中挖掘与数学有关的内容，合理融入数学教学中，既可以拉近学生与数学的距离，又能将数学教育与美育相连，实现情感、态度和价值观的需求，使数学教育的目标从育智走向育人. 我国数学教育不公平现象主要源于城镇、学校地区教育资源分配不公等. 但互联网的发展为教育教学资源分配创造了新的切入口. 利用教育资源云平台可以实现优质数学教育资源的流通，还能打破时间和空间上对数学学习的限制. 因此，加强平台建设、创建数字化资源等理应成为教育改革的重要任务之一.

实施公平教学应该从我国实际国情出发，进行本土化的顶层设计. 实际上，国家层面近几年已经出台了大量文件、政策来推动教育公平进程. 因此，更关键的是“落地”问题，根本落脚点回到了数学本身，需要教师进一步深度理解和挖掘数学内容. 数学课程标准提供了数学教学的内容标准、要求，以及教学、评价建议等. 在实际教学中，还需要结合学生的情况、教师自身的实际不断细化. 公平意识应该贯穿教师的整个教育教学过程，无论是数学内容的解读、教学任务的安排，还是教学活动的设计、学生学习的评价，都要面向全体学生. 除了公平，追求成效亦是数学教育的目标，但两者往往会出现矛盾和沖突，故而需要妥善处理好两者之间的关系，力图寻求两者共同价值的最大化. 值得注意的是，追求教育教学公平绝不是教师这一单独的群体，而需要整个教育事业共同体的努力，共同支持教师实施公平性教学.

2. 强调学生参与，使之真正成为数学学习的主人

学生的参与需要以兴趣为引导，并关注学生的提问. 数学的高度抽象性和严谨性导致数学学习难度较大，也使得大多数学生在数学学习过程中产生了畏难情绪. 实际上，数学是平易近人、富有趣味的. 数学教师的工作就是要把数学讲活，深入浅出、举重若轻地揭示数学的本质. 教师应该充分考虑学生学习的特点，合理设置数学教学情境，既可以从数学史中采撷先辈的宝贵经验作为背景，也可以从与学生密切相关的实际生活中寻找教学载体，力求教学情境真实、真诚，从而引起学生对数学学习的关注与兴趣，激活学生的学习内驱力. 教学过程中，还要发挥学生猜想和提问的价值，给予及时的评价与反馈，并鼓励学生合理质疑，这有助于发展学生的逻辑思维和推理论证能力.

学生参与教学活动要依托开放式任务，扎根深刻的思考. 开放式任务因其难度跨度大，可以满足更多学生的需求，提高课堂上学生的共同参与度. 分层教学容易损害学生的学习动机，造成不适合学习数学的错误归因或固化心态. 而在同一任务情境下，能相对减少这类问题的出现，使学生产生数学学习的归属感，主人翁意识得到强化. 开放式任务有助于合作学习与数学对话的开展，学生的数学活动经验在合作中得到积累，数学思维在表达中变得更加清晰，积极的交流也将加速信息的反馈流动，为教师观察学生、进行及时性评价提供多维度的信息. 数学学习高度强调智力参与，故关注学生的独立思考更应该成为开放式任务的核心与重点. 教学过程中不能流于讨论、合作形式上的热闹，更应该引导学生重视自身的深入思考. 因此，数学教育改革过程中要大力开发有价值的开放式任务，让多种教学方式服务于学生的独立思考.

3. 聚焦核心概念，实现数学教学内容体系的重构

（1）数学学习要回归概念，夯实数学的基础知识和基本能力.

数学不是零散的知识点和大量公式定理的拼盘，而是具有联系的一个整体. 核心概念具有串连数学知识的作用，在强调联系的同时还会渗透数学思想方法，可以帮助学生形成良好的数学认知结构. 聚焦核心概念，能为学生揭示知识与知识之间的联系，提供解决问题的线索，便于知识的迁移. 现实教学中一个很大的问题就是深陷题海战术，这样拘泥于一招一式的教学方式很难使学生获得可持续发展，从而适应未来社会的发展需求. 要想让学生从繁重的练习中解脱出来，就需要回归核心概念的教学，在加深对数学本质解读的基础上，不断夯实基础知识和基本能力.

（2）优化教材价值，重构数学教学内容体系.

教育数学是教育形态的数学，能够激发学生火热的思考，提高知识的接受度和思考的效率，从而让数学化难为易. 聚焦核心概念和教育数学实则殊途同归. 由于教材始终不可避免地不能与社会发展达成完全同步，就必然需要教师对教材进行二次开发. 实际上，从核心概念出发，为数学的改造提供了一种技术手段，可以将数学课程标准作为主线，通过研讨、调查与实践多方探索总结出核心概念与大观点，完善数学教学内容体系，使相对零散的扁平式学科知识向网状立体式结构转变. 教师理解不同年级、不同模块的核心概念，有助于了解学生已经学习了什么，将来学习什么，从数学内部提供了对学生学情预测的视角.

4. 关注教师发展，提供支持并完善专业成长体系

（1）优化数学教师专业成长体系，提供多方必要支持.

教育大计，教师为本. 牢牢把握教师这条改革路径是提高教学质量的必经之路. 对此，可以参考美国在数学教师发展三个不同阶段所考虑的重要因素中的可取之处. 要实现教育强国就需要教师改变自己传统的教育观点与认识，积极发挥自身的主观能动性，树立主动寻求专业学习的意识，而不再是被动地参与培训. 建立教师专业学习的相关标准，并为教师提供必要的保障，使得教师的专业学习成为一个持续参与的过程.

（2）教师专业发展过程中的学习内容、形式等应尽可能多元化.

学习内容应凝结先进教育理论与数学学科认识，要符合一线教师的需求，能真正落实于实际教学中，解决理论与使用场景不适配的问题. 除此之外，专业学习内容还需要紧跟时代步伐. 信息化教学已然成为未来教育的趋势，数学教师应该掌握必备的信息化教学手段，提升信息素养. 由于在职教师日常教学任务繁重，而且短期的讲座式培训系统性不强. 因此，应该注重数学教研在教师专业发展中的作用，不断迈向常态化，并在此过程中完成个人反思和集体反思. 同时，借助互联网优势，开展线上专业学习，并为高校数学教育专家、科研人员与一线教师搭建及时沟通交流的桥梁，这将促进理论与实践的紧密联系，使得每位数学教师向专家型教师靠拢，提升数学教师队伍整体水平. 推动师范生教育改革，做好教师质量托底保障. 加大师范生的课程改革力度，帮助师范生积累扎实的面向教学的数学知识，并通过师范生与一线教师的联动，使得教育体系焕发新的活力与生机.

参考文献：

［1］California State Board of Education. The Draft Mathematics Framework［EB / OL］. ［2021-5-15］https：//www.cde.ca.gov/ci/ma/cf/index.asp.

［2］中华人民共和国教育部制定. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［3］张奠宙. 教育数学是具有教育形态的数学［J］. 数学教育学报，2005，14（3）：1-4.

［4］黄舒娴，胡典顺，朱少卿. 美国《加利福尼亚州数学框架·评价》简介及启示［J］. 数学通报，2015，54（3）：3-7，2.

［5］叶珂，胡典顺. 美国《加利福尼亚州数学框架·教学策略》简介与启示［J］. 数学通报，2016，55（1）：6-11，16.

［6］王静，胡典顺，叶珂. 美国《加利福尼亚州数学框架·技术》简介及启示［J］. 中国数學教育（高中版），2016（11）：60-64.

收稿日期：2022-07-13

作者简介：唐浩松（1998— ），男，硕士研究生，主要从事数学教育和比较教育研究.