论中考数学中一类典型的直线型轨迹问题

李宝娜　赵继仙

【摘 要】动点轨迹问题是中考数学经常考查的重要知识点。文章以简单的直线型动点轨迹为例，从简单到复杂，总结出此类问题的特征，并给出此类问题的一般解题思路，最后以中考真题进行模拟演练，以帮助学生熟练掌握找动点轨迹的思路和方法。

【关键词】中考数学;直线型轨迹问题;动点轨迹

【中图分类号】G633.6  【文献标识码】A  【文章编号】1671-8437（2022）24-0090-03

“种瓜得瓜，种豆得豆”经常用来形容种了什么因，就得到什么果。生活中有大量这样的例子，如经常锻炼的人会有好的身体、勤劳的人生活水平会提升。数学中也有这样的例子，如图1，直线l上任一点A与直线外一定点O相连，取OA中点B，当主动点A在直线l上运动时，从动点B运动产生的轨迹也是一条直线。这其实就是“种瓜得瓜，种豆得豆”的一种表现，因此可以称之为“瓜豆原理”，常用来找从动点的轨迹[1]。

本文围绕中考数学一类典型的直线型轨迹问题，从简单到复杂，逐渐增加要素，引导学生探索动态变化过程中的变与不变，进而得出“直线型瓜豆原理”的一般结论。

1   解题思路探究

1.1  基础认知

解题前要明确一个事实：动点与某定点的连线和定直线的夹角固定不变时，动点的轨迹为直线。

1.2  “瓜豆原理”解题思路探索

本文例子的分析重点在于引导学生对此问题进行一般性探索，首先掌握探索的方法，其次才是结论的总结。

例1：如图2，O为定点，点P是直线AB（图中为线段，便于探索轨迹长度）上一动点，连接OP，点Q是OP上一点;当Q满足为OP中點时，随着点P在直线AB上运动，点Q的轨迹是什么？

分析：主动点P的运动导致从动点Q的运动，应采用从特殊位置开始分析，再联系一般位置的方法进行探索。

第一步，找出主动点P的初始位置，画出初始图形，如图3，图中P0、Q0、OP0均固定。第二步，利用初始位置和任意位置，借助中位线（相似模型），证明动点位置轨迹关系。连接Q0Q，如图3利用中位线得到Q0Q∥AB，依据Q0定点、AB定线，可以得出Q0Q位置固定（实际是过定点Q0，且与定线OQ0成固定夹角）。第三步，利用初始位置和终止位置，得到动点轨迹长度关系式。如图4，图中P1、Q1、OP1均固定，利用中位线得到Q0Q1∥AB且Q0Q1=AB。动点Q的轨迹为直线（上一部分），且Q的轨迹长度是P点轨迹长度的一半。

由于中点具有特殊性，为不失一般性，因此在OP上任取一点进行下一步的分析。

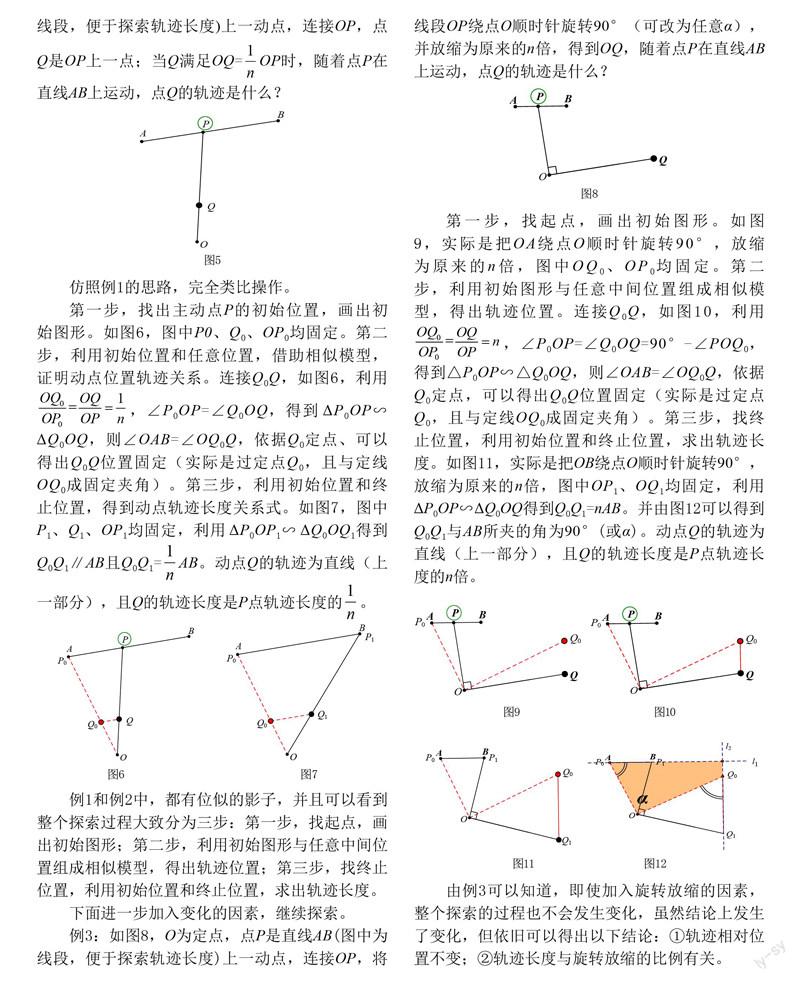
例2：如图5，O为定点，点P是直线AB（图中为线段，便于探索轨迹长度）上一动点，连接OP，点Q是OP上一点;当Q满足OQ=OP时，随着点P在直线AB上运动，点Q的轨迹是什么？

仿照例1的思路，完全类比操作。

第一步，找出主动点P的初始位置，画出初始图形。如图6，图中P0、Q0、OP0均固定。第二步，利用初始位置和任意位置，借助相似模型，证明动点位置轨迹关系。连接Q0Q，如图6，利用，∠P0OP=∠Q0OQ，得到 ΔP0OP∽ ΔQ0OQ，则∠OAB=∠OQ0Q，依据Q0定点、可以得出Q0Q位置固定（实际是过定点Q0，且与定线OQ0成固定夹角）。第三步，利用初始位置和终止位置，得到动点轨迹长度关系式。如图7，图中P1、Q1、OP1均固定，利用 ΔP0OP1∽ ΔQ0OQ1得到Q0Q1∥AB且Q0Q1=AB。动点Q的轨迹为直线（上一部分），且Q的轨迹长度是P点轨迹长度的。

例1和例2中，都有位似的影子，并且可以看到整个探索过程大致分为三步：第一步，找起点，画出初始图形;第二步，利用初始图形与任意中间位置组成相似模型，得出轨迹位置;第三步，找终止位置，利用初始位置和终止位置，求出轨迹长度。

下面进一步加入变化的因素，继续探索。

例3：如图8，O为定点，点P是直线AB（图中为线段，便于探索轨迹长度）上一动点，连接OP，将线段OP绕点O顺时针旋转90°（可改为任意α），并放缩为原来的n倍，得到OQ，随着点P在直线AB上运动，点Q的轨迹是什么？

第一步，找起点，画出初始图形。如图9，实际是把OA绕点O顺时针旋转90°，放缩为原来的n倍，图中OQ0、OP0均固定。第二步，利用初始图形与任意中间位置组成相似模型，得出轨迹位置。连接Q0Q，如图10，利用，∠P0OP=∠Q0OQ=90°-∠POQ0，得到△P0OP∽△Q0OQ，则∠OAB=∠OQ0Q，依据Q0定点，可以得出Q0Q位置固定（实际是过定点Q0，且与定线OQ0成固定夹角）。第三步，找终止位置，利用初始位置和终止位置，求出轨迹长度。如图11，实际是把OB绕点O顺时针旋转90°，放缩为原来的n倍，图中OP1、OQ1均固定，利用ΔP0OP∽ΔQ0OQ得到Q0Q1=nAB。并由图12可以得到Q0Q1与AB所夹的角为90°（或α）。动点Q的轨迹为直线（上一部分），且Q的轨迹长度是P点轨迹长度的n倍。

由例3可以知道，即使加入旋转放缩的因素，整个探索的过程也不会发生变化，虽然结论上发生了变化，但依旧可以得出以下结论：①轨迹相对位置不变;②轨迹长度与旋转放缩的比例有关。

接下来以一个具体题目为例开展演练，进而总结题目满足什么条件、结论具有什么特征。

例4：如图13，在正方形ABCD中，AB=1，P是边BC上的一个动点，由点B开始运动，运动到C停止。连接AP，以AP为直角边向右侧作等腰直角三角形，另一个顶点为Q。则点P从B运动到C的过程中，点Q的运动路径长为__________。

该题依旧有动态的变化，因此仍采用“特殊联系一般”的分析方法。第一步，找起点，画出初始图形。如图14，点P的初始位置为B，此时以AP为直角边作的等腰直角三角形即为△ABC。第二步，利用初始图形与任意中间位置组成相似模型，得出轨迹位置。连接CQ，如图15，利用，∠BAP=∠CAQ=45°-∠PAC，得到ΔBAP∽ΔCAQ，则∠ABP=∠ACQ=90°，由AC为定线，可知Q始终在固定直线上运动。第三步，找终止位置，利用初始位置和终止位置，求出轨迹长度。如图16，点P的终止点为C，此时以AP为直角边作的等腰直角三角形记为ΔACE，从图形位置可以直接得点Q的轨迹为CE，长度为。

仿照前面4个例题，把点Q的运动（CE）与点P的运动（BC）联系在一起。利用，

∠BAC=∠CAE=45°，得ΔBAC∽ΔCAE，得到，即得到动点Q的轨迹为直线（上一部分），且Q的轨迹长度是P点轨迹长度倍。

实际上，例4为例3的一种情况：主动点P在定线段BC上运动，连接AP后，将AP绕点A逆时针旋转45°，并扩大为原来的倍，得到从动点Q，则点Q运动轨迹也为线段（且与点P轨迹夹角为45°），且点Q的轨迹长度是点P轨迹长度的倍。由此可见与题目是否描述为旋转没有关系。

1.3  “瓜豆原理”解题思路总结

通过前面例题的探索，可以得出一个关于“瓜豆原理”的结论：分析背景条件后，若主动点P、从动点Q与定点A连线的夹角为定值（可以看作旋转角，记为α），且从动点Q、主动点P与定点A连线的比值为定值（不妨记），则从动点Q的轨迹与点P保持一致，即当点P在线段上运动时，可以得到如下结论：①点Q在线段上运动;②运动轨迹的夹角α，从动点轨迹长度与主动点轨迹长度的比值为定值k。

2   总结

动点轨迹问题是中考数学经常考查的重要知识点，同时也是学生纵向调用知识的难点，本文不断添加变化的条件、提取特征、总结方法的整个过程是可以迁移的。

“瓜豆原理”既是结论，也是探索过程，尤其当中涉及化动为静、动静结合的操作原则以及“从特殊到一般”的探索方法，是初中学生在数学学习过程中务必要掌握的内容。

【参考文献】

[1]何华军.凸显思维过程，提升解题能力——对一道直线型轨迹问题的探究[J].初中数学教与学，2020（11）.

【作者简介】

李宝娜（1988～），女，汉族，河南安阳人，硕士研究生，助教。研究方向：应用数学。

赵继仙（1991～），女，汉族，河南洛阳人，硕士研究生，助教。研究方向：思想政治教育。