艺术工匠的几何创想

张羿

很久以前，他在一次游历中偶然发现了这个领域（平面规则分割）。他仿佛看到了一堵高墙，预感到一些东西可能隐藏在高墙之后，他艰难地爬了过去。然而，在另一边，他落在了一片荒野上，不得不劳神费力地开路，直到发现一条迂回路线，来到了一扇敞开的大门，这是数学的大门……

1922年，一位落魄青年画家来到西班牙阿尔罕布拉宫，宫内精美繁复的装饰图案令他赞叹不已，他跃跃欲试想要模仿，但茫无头绪，只好无奈放弃。但这次邂逅在他的心中种下了一颗灵感的种子。十余年后，他故地重游，又一次看到阿尔罕布拉宫的精美装饰，此后就仿佛打开了绘画的任督二脉一般，他创作了无数极富数学韵味的版画作品而声名大噪，成为科学家推崇的艺术家。曾经的荷兰女王冬季行宫也被改造成以他的名字命名的博物馆，里面陈列着他的作品，供后人参观纪念。

想必你已经猜到了，此人就是荷兰版画家莫里茨·科内利斯·埃舍尔（Maurits Cornelis Escher）。那么，他究竟在这座北非摩尔人建造的宫殿中找到了什么灵感之泉，让他茅塞顿开，从此逆天改命？

答案是铺满阿尔罕布拉宫中各面墙壁的几何图案。只见彩色釉面砖铺满整面墙壁，形成漫无边际、繁复迷离却又秩序井然、美轮美奂的几何图形。这些几何图形变化循环，组成的图案包罗万象、云谲波诡，令人啧啧称奇。

而在埃舍尔看来，这些填满平面的彩釉瓷砖，与其说是在描绘抽象的几何形体，不如说是在意图创造一些可辨认的形体。他在自己的著作《平面规则分割》中写道：

？？摩尔人是平面镶嵌的大师，他们能够用

全同的几种图案镶嵌整个平面而不留任何空

隙。尤其是在西班牙的阿尔罕布拉宫，他们

把几种彩釉瓷砖纤毫不差地拼在一起，装饰

墙壁。不过很遗憾，伊斯兰教禁止造“像”。

所以在他们的镶嵌画中，他们只能把自己的

想象力限制在一些抽象的几何形状里。据我

所知，没有一个摩尔艺术家胆敢（甚至想都

不敢想）用具体的、可识别的图形，如鸟、鱼、

蜥蜴和人类的形象作为镶嵌图案的基本元素，

但是对我来说，这种限制是难以接受的，因

为在我自己的图案中，正是基本元素的可识

别性，才是我对这个领域爱不释手的原因……

平面规则分割是我挖掘出来的最丰富的灵感

之泉，它至今也没有枯竭。

埃舍尔所谓的“平面规则分割”就是数学中的“平面密铺”概念，即用不同的几何形状完全覆盖一个二维平面，而且图形之间既没有重叠，也没有缝隙。简而言之，就是贴砖。人类离开洞穴后，自己建造房屋，他们开始用石头来铺砌地面和墙壁。当人们开始选取各种形状和颜色的石头来做漂亮的设计时，就可以把贴砖看作是一种艺术了。然而，时至今日，贴砖似乎只是装修工人们的无聊活计。在地面上、墙壁上，各样的贴砖随处可见，它们即便不是千篇一律，也是平淡无奇。不过也正因为如此，阿尔罕布拉宫中的精美密铺图案才显得尤为珍贵，也成为埃舍尔“最丰富的灵感之泉”。

想必你一定好奇，如此精美繁复的图案，工匠们是如何创作出来的？

显然，十几个世纪以来，伊斯兰几何设计的历史经历了从简单到复杂的连续演变过程，期间诞生的创作方法也绝非唯一。这些设计者具备高水平的应用几何学知识。但是很遗憾，他们都没有兴趣通过证明定理和建立关于此类设计的数学知识，来提供科学的绘制方法。他们并不像如今的技术人员一样编写开发秘籍，也不像画家一样留下天马行空的手稿。这些伊斯兰几何天才们的设计，具体时间不明，诞生地点不明，创作者不明，发展进程不明……总之除了如今留在文物古迹上的作品，一切都不明！

艺术方法论是一切严肃艺术研究的一个重要方面。详细了解传统艺术家、手工艺人和建筑师所使用的方法和技术，可以使我们更全面地了解某一艺术门类中的大趋势以及细微差别。了解历史设计方法论可以让我们对伊斯兰几何图案设计传统的最初发展、完善、成熟，以及对地理分布有更深入的认识。然而，随着这种装饰传统在历史上日趋衰落，关于制作复杂图案的方法的知识也随之被逐渐遗忘。即使从20世纪下半叶开始，人们对伊斯兰几何图案的兴趣有所重燃，但由于缺乏对历史设计方法论的了解，恢复对这种艺术形式的尝试也困难重重。

方法论知识的缺失让鉴赏者和有兴趣将这种设计融入自己作品中的创作者如坠云雾之中，就像第一次游历阿尔罕布拉宫的埃舍尔一样，经历过一系列徒劳的尝试之后，只得无奈放弃。这些精美繁复的图案仿佛一条没有尽头的苦难之路，看不到一抹亮色，也不知道尽头在何方。

大多數时候，创作灵感是直觉的产物，而理性却总是姗姗来迟。即便是埃舍尔这样的天才，也和常人无异。

很久以前，他在一次游历中偶然发现了这个领域（平面规则分割）。他仿佛看到了一堵高墙，预感到一些东西可能隐藏在高墙之后，他艰难地爬了过去。然而，在另一边，他落在了一片荒野上，不得不劳神费力地开路，直到发现一条迂回路线，来到了一扇敞开的大门，这是数学的大门……

埃舍尔找到数学之门的“迂回路线”始于他第二次游历阿尔罕布拉宫之后不久，当时埃舍尔经常到父母在海牙的家中做客。在这里，他遇到了同父异母的兄弟、莱顿大学地质学教授比尔·埃舍尔。埃舍尔同他的兄弟聊起了自己在平面规则分割领域的工作，比尔表示晶体学家也在研究类似的问题，建议他阅读相关科学文献与成果。

于是，这位比尔就成了将埃舍尔的研究与理性的科学联系起来的人，正是他为埃舍尔指出了“敞开的大门”。埃舍尔听从比尔的建议，阅读了大量数学家和晶体学家的成果，然后就找到了通往平面规则分割的数学大门，并打开了它。入门之后，他开始开辟新道路，走向那些被数学家和晶体学家忽视的领域。他在《平面规则分割》中写道：

？？在数学领域，平面规则分割已经在理论

上得到了充分的研究……数学家打开了一扇

通向无限可能性的大门，但是他们自身并没

有进入其中。他们的特殊禀赋使他们对打开

这扇门的方式更感兴趣，而对隐藏在其后的

花园不感兴趣。？

在埃舍尔看来，在这个花园里耕耘播种自然是艺术家的工作。他开发了一套“外行人的理论”，作为自己进行平面规则分割创作的方法论。

接下来，我们就以阿尔罕布拉宫中的一些墙面装饰图案为例，跟随埃舍尔的脚步，用他那套“外行人的理论”，走进平面规则分割的花园。

如图3，以正方形作为密铺单元，对其进行改造。左侧割掉一个梯形，绕A顺时针旋转90°补到下方；右侧也割掉一个梯形，绕C顺时针旋转90°补到上方，从而得到一个哑铃形图案。显然，这个哑铃形图案可以密铺平面。

图4仍然以正方形作为密铺单元。左侧割掉一个三角形补到上侧；下侧也割掉一个三角形补到右侧，得到了帽子形密铺图案。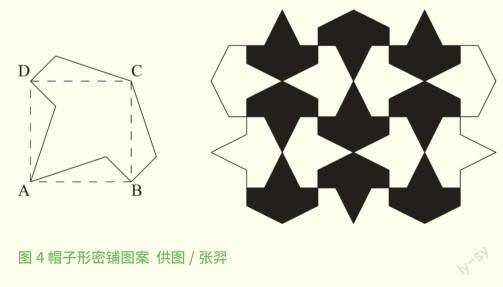

图5将图4稍作修改，将割补三角形的一条边变成弧线，得到了飞机形密铺图案。

图6在图5基础上再作修改，将割补三角形的两条边都变成弧线，得到了枫叶形密铺图案。

图7将割补三角形的尺寸变小，得到了鱼形密铺图案。

圖8以正三角形作为密铺单元进行改造。在正三角形底边一侧割下一个弓形，围绕底边中点旋转180°补到另一侧，另外两条边同理，得到了回旋镖形图案。

由此可见，埃舍尔的方法是通过“改造”基础的密铺单元衍生出较为复杂的图案。“改造”就是利用基础多边形的对称特性，进行平移、旋转、反射、滑移反射等容变换操作。所谓等容变换，顾名思义，就是指把一个多边形变来变去的最高原则是必须保持多边形的面积不变。如果一侧变形，那么另一侧就必须进行相应的变形来补偿。可以用一句诗来形容：下面凹来上面凸，左边割掉右边补。

正是此法，让埃舍尔把大千世界中多姿多彩的花鸟鱼虫、飞禽走兽密铺到平面之中，令人拍案叫绝。