构建几何模型 秒杀中点问题
蔡忠平

D
由中点可以联想等腰三角形“三线合一”、直角三角形斜边上的中线、三角形的中位线等知识. 李英豪老师在《中点用法》直播课中,构建了与中点相关的几何模型,能够帮助同学们根据不同条件作出恰当的辅助线,从而解决与中点相关的几何问题.
模型构建
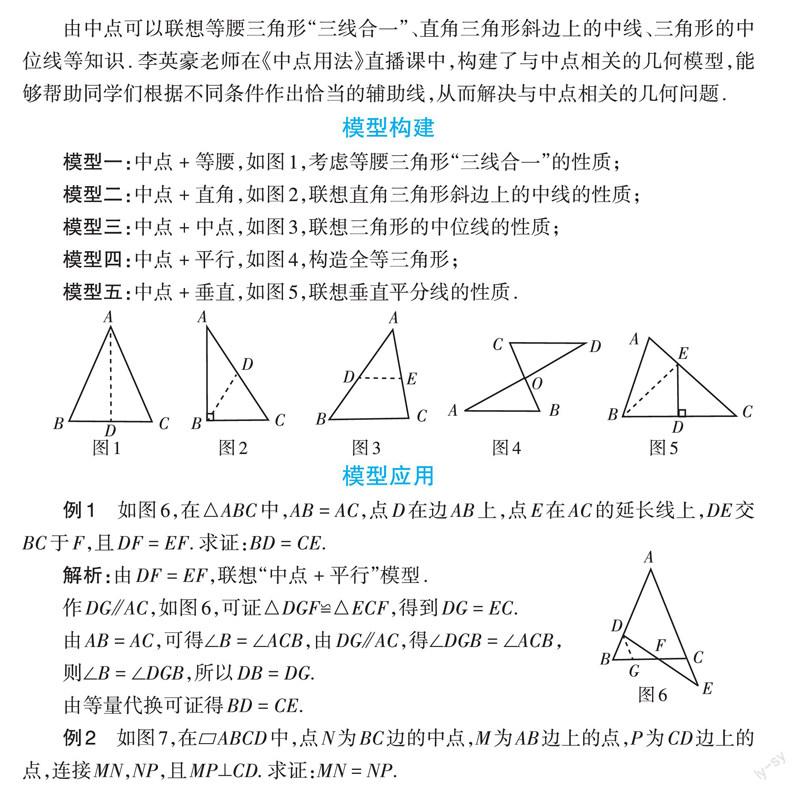
模型一:中点 + 等腰,如图1,考虑等腰三角形“三线合一”的性质;
模型二:中点 + 直角,如图2,联想直角三角形斜边上的中线的性质;
模型三:中点 + 中点,如图3,联想三角形的中位线的性质;
模型四:中点 + 平行,如图4,构造全等三角形;
模型五:中点 + 垂直,如图5,联想垂直平分线的性质.
模型应用
例1 如图6,在△ABC中,AB = AC,点D在边AB上,点E在AC的延长线上,DE交BC于F,且DF = EF. 求证:BD = CE.
解析:由DF = EF,联想“中点 + 平行”模型.
作DG[?]AC,如图6,可证△DGF≌△ECF,得到DG = EC.
由AB = AC,可得∠B = ∠ACB,由DG[?]AC,得∠DGB = ∠ACB,
则∠B = ∠DGB,所以DB = DG.
由等量代换可证得BD = CE.
例2 如图7,在?ABCD中,点N为BC边的中点,M为AB边上的点,P为CD边上的点,连接MN,NP,且MP⊥CD. 求证:MN = NP.
解析:由?ABCD和BN = CN,联想“中点+平行”模型.
如图7,延长AB,PN交于点G,
易证△PCN≌△GBN,可得PN = GN.
由AB[?]CD,得∠GMP = ∠DPM = 90°.
联想“中点 + 直角”模型可得MN = [12]PG = NP.
例3 如图8,点B为线段DC上的一点,分别以DB,BC为直角边作等腰直角三角形DBE和等腰直角三角形ABC,连接AE,取AE的中点F,连接DF,CF,試判断DF与CF有怎样的关系.
解析:由题意知∠EDB = ∠ACB = 90°.
由点F是AE的中点,联想“中点 + 平行”模型.
延长CF,DE,交于点G,
可证△ACF≌△EGF,得AC = EG,CF = GF,从而可证DC = DG.
联想“中点 + 等腰”模型,可证得DF⊥CF,DF = CF.
例4 如图9,在四边形ABCD中,∠DAB = 90°,∠DCB = 90°,点E,F分别是BD,AC的中点,AC = 6,BD = 10,求EF的长.
解析:连接AE,CE,由∠DAB = ∠DCB = 90°,点E是BD的中点,联想“中点 + 直角”模型,可得EA = EC = [12]BD. 由点F是AC的中点,联想“中点 + 等腰”模型,可得EF⊥AC. 在Rt△AEF中,根据勾股定理,可得EF = 4.
分层作业
难度系数: ★★★解题时间:15分钟
1. 如图10,在Rt△ABC中,∠ACB = 90°, BC = 3, AC = 4,点D为AB的中点,过点D作DE⊥AB,交BC的延长线于点E,则CE的长为. (答案见第37页)
2. 如图11,点M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB = 10,MN = 3,BC = 15,则△ABC的周长为. (答案见第37页)
3. 如图12,在Rt△ABC中,∠BAC = 90°,BC = 4,E,F分别是BC,AC的中点,延长BA到点D,使AD = [12]AB, 连接DE,DF,则DF的长为. (答案见第37页)

