用什么撬动“量感”培养

许贻亮 朱阿娜

【编者按】量感源自度量，主要是指对事物的可测量属性及大小关系的直观感知，也表现为学生在现实情境中主动运用量的意识。当前，越来越多的教师开始关注对学生量感的培养，但在实践中却遇到一些困惑。那么，量感与数感有何区别？量感的核心概念是什么？教学中应采用何种策略应对学生量感发展的需求？本期一起来探讨这一话题。

提到“量感”，一线教师难免会有“熟悉的陌生”之感。熟悉的是，现行教材中的各种度量教学内容，包括生活中的人民币、质量、时间，图形中的长度、角度、面积、体积等。陌生的是，原有的度量教学算不算对量感的培养？是否达成《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）中提出的“对事物的可测量属性及大小关系的直观感知”及相关培养目标？特别是在除长度、面积、体积外，其他度量教学内容都移到“综合与实践”领域之后。观念是行为的先导，认识观念不清，教学行为则难免走样。我们以为，原有的度量教学与核心概念的量感培养之间不能简单画上等号，它们既有联系又有区别。孔企平教授指出：“量感”与“度量”的关系就好比“数感”与“计算”的关系。那么，教学中如何架设撬动“量感”培养的支点？笔者认为，教学支点的架设应是多维、综合、整体地考量。在教学材料的全局设计中夯实支点的基体，由度量本质的深刻体验中提炼支点的刚性，从核心素养的整体落实中校准支点的方向，三者共同发力，更好地为培养学生量感服务。

一、设计教学材料，夯实支点的基体

要实现量感培养，应重视对教学材料的设计，从而夯实教学支点的基体。要把现行教材内容深度加工为教学材料，即在深入理解教材的学习主题、基本线索、认知结构的基础上，结合学情调研、教学思考、课程目标等，对教材内容进行“照用”“截用”“重用”等综合性使用。以设计好的教学材料，在教与学之间，在课堂教学与课程目标之间织好纽带、架好桥梁、搭好平台。

“什么是面积”一课中，第1个情境问题串是“看一看，比一比”，安排了3组教学素材：①大小相等、形状相同的语文、数学课本;②大小不等、形状相同的两枚硬币;③大小不等、形状不同的两片树叶。细分析，可以发现其中的逻辑脉络：从规则图形到不规则图形，从形状相同到形状不同，从直接观察判断到重叠操作判断，进而归纳概括面积的概念。其教学的核心有二：一是揭示面的所在，面的形状;二是揭示有的面大，有的面小。从外延与内涵两方面来建构面积概念，形成丰富表象。这样编排符合学生的认知规律，教学是可以按这样的教学素材编排脉络循序推进的。在教学材料的深加工中，我们对这3组素材的使用并不是平均用力，而是在“照用”教材的同时对第1组素材进行“重用”，以此夯实基体，再顺延到其他2组素材。需要说明的是，对教学材料的深加工不仅存在于课堂教学的情境创设阶段，而是涵盖着整个教学过程，需要整体性、全局性地统筹、取舍与布局。

实际教学中，我们通过对第1组素材的深度加工，强化学生对“面”的多元感知，组织了4个数学活动。其一，增补。从语文书、数学书2本的简单相等，增补数量到6本，包括3本教科书（语文、数学、英语）和3本练习本（生字本、算术簿、英语书写本），拓展规则物体形状的外在表征，把教材中第2组素材的教学要素（大小不等，形状相同）融合进来，实现融多为一。其二，分类。把这6个教学素材进行分类，直击面积的核心要素“面的大小”，在直观中唤醒学生已有的生活经验，自然地引出“面积”，并在操作中确定3本教科书封面一样大，3本练习本封面一样大，有机渗透观察法、重叠法。其三，刷面。让学生把手想象成一把神奇的“刷子”，刷出数学书封面的面积。刷的过程中，从只刷一点点（不满），到一不小心刷过头了（超出），最后完整地刷出整个面积（刚好），在3次情况对比中更好地确认面的具体大小，即“横向到边，纵向到底”，从而确立面积的内涵。其四，拓展。以图片及实物的形式，从硬币、树叶，到长方形、圆柱等，从物体表面到平面图形，从规则的面到不规则的面，从直面到曲面，在外延的拓展中完善面积的丰富表象。

从一年级认识图形知道“面在体上”，到二年级对长方形、正方形特征的认识，其实对面的感知学生并不陌生，但深入地、微观地认识面的二维属性，本课却属首次。在学情调研中，我们发现许多学生存在认知上的困难或偏差。有的把面指为一个点或一条线，有的则只是笼统地说“面在这儿”等，显示出学生已有经验中对“面”及“面的大小”感知的浅层或模糊。为此，本课教学一开始就设计6样学习用品（教科书、练习本），让学生在熟悉的教学材料中一下子就关注到面及其大小，在观察、分类、重叠中给予二次确认，再组织有趣的浸入式体验把面刷出来，直观感受面的边界范围，让学生既动手又动脑，使量感的培养深入到学生的认知兴趣与具身体验中。因此，通过有层次性的、融合性的教学材料，夯实教学支点的基体，可以实现学习中“知”与“情”的双促进与双收获。

二、深刻度量本质，提炼支点的刚性

要推进量感培养，应突显学生对度量本质的深刻体验，提炼教学支点的刚性。量感与度量之间虽不能简单地画上等号，但度量始终是量感培养的重要教学内容，包括度量意识、度量单位、度量工具、度量方法、度量公式等。华罗庚先生指出：“量（liàng）”起源于“量（liáng）”，“量”是度量的结果，可以用“数+度量单位”表达。可见，度量单位是“度量”的核心要素。具体到面积来说，就是要确定面里有几个这样的度量单位，实现从定性感知到定量刻画的认知提升。

“什么是面积”一课，教材在第2个情境问题串中安排了长方形和正方形的面积比较，并提供3种不同的比较策略：①量边长，②剪、拼，③用小正方形度量。这些策略分别指向一维属性的周长与二维属性的面积，既有定性的比较方法（剪、拼），也有定量的刻畫方法（量边长、用小正方形度量）。但在日常教学中，这一“定性”到“定量”的过程，常见学生在教师要求下的“依令而行”，特别是“用小正方形度量”时，学生缺乏“会针对真实情境选择合适的度量单位进行度量”的解决策略思考力，表现更多的是动手操作执行力。教学支点的刚性不足，不利于量感的长远发展。

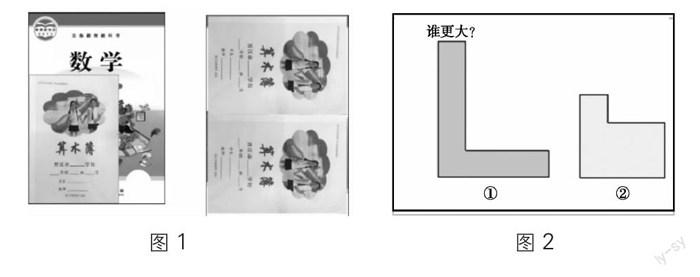
《课程标准》在“教学提示”中强调，要让学生“经历选择面积单位进行测量的过程，理解面积的意义”。实际教学中，在揭示面积概念后，我们展开两次度量活动。其一，通过对教学材料的一材多用，组织学生观察、猜测：“数学书封面比算术簿大多少？”实现从“多这么多”到“2倍关系”的转变（如图1），不仅发展学生观察比较的变通力，深刻感知“算术簿封面的面积为1，数学书封面的面积为2”的数学表达更为精确、准确，初次感受定量刻画的价值，又以此顺势迁移到其他的度量方式，如用小正方形度量获得数值6等，在丰富学生度量策略的同时进一步感知面积的数值表达。其二，出示一组不规则的图形（如图2），组织学生对它们的面积大小展开比较。多数学生结合观察到的图形特点，联系度量经验，自发地提出解决问题策略“用小正方形来量”，这时教师再提供学具支持，从而化“形”为“数”，用数据说话。通过实际度量，最终赋予两个图形面积数值“8”和“7”，再次加深对图形面积的定量把握。

从算术簿的“非标准量度量”到小正方形的“半标准量度量”，教学中始终围绕度量单位展开，在操作的具身体验中渗透培养了“我要度量”的意识和数学眼光。对于图2的教学，虽然没有过多地强化度量工具的多样性选择（如小正方形、方格纸、圆片等），却在简单中达成深刻，在朴实中实现通透，使学生对度量意识、度量单位、度量价值的体验更为充分，从而更深层次地滋养学生的量感发展。因此，通过紧扣度量本质展开，使学生的量感体验厚实起来，提炼教学支点的刚性，可以实现以简驭繁的教学效果。

三、落实核心素养，校准支点的方向

要实现量感培养，应紧盯核心素养的具体落实，校准教学支点的方向。《课程标准》指出：“课程目标的确定，立足学生核心素养发展，集中体现数学课程育人价值。”小学生的数学核心素养具有“整体性、一致性和阶段性”，应在每一节课中始终给予关注与落实。对此，我们既要有基于核心观念的备课意识，也要有单元整体教学的战略眼光。具体到“什么是面积”一课，我们不能仅把它定位为一节概念课，不能仅关注它的内涵与外延，不能仅把学生的思维触角局限于能比较出两个面的大小。而应该有更宽广的教学视野、更清晰的目标导向，把它当作基于“面积”培养“量感”，进而整体落实数学核心素养培养的有机部分。

解读“什么是面积”教材中第3个情境问题串及“练一练”的教学内容，可以发现其中蕴含着变中不变、转化等数学思想，以及对空间观念、推理意识等核心概念的感悟，这是我们教学“图形与几何”领域要始终关注的数学核心素养。虽然各核心概念的侧重点有所不同，但教学中应该把它们与量感培养一并考虑、落实。

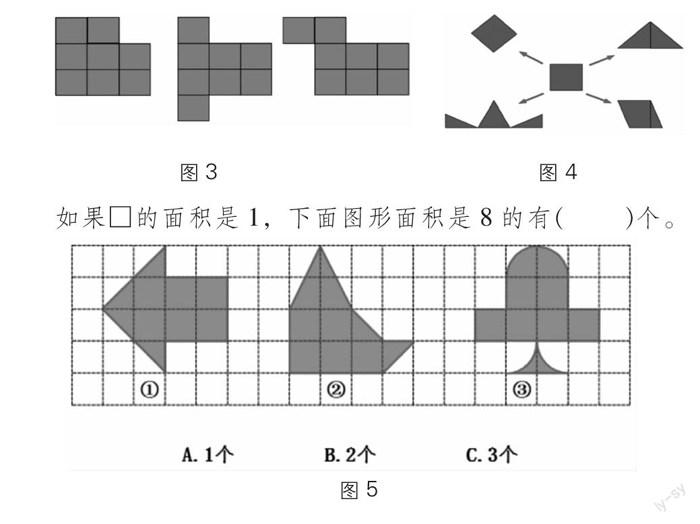
实际教学中，在赋予图2中1号图形、2号图形面积大小的数值后，我们组织两次延伸性思考。其一，“能使这两个图形面积一样大吗？”在所加上的1个小正方形的不同擺放方法中，让学生感受度量中的“图形面积的可加性”，体会变中不变的数学思想（如图3）。其二，“加上去的这1个小正方形一定是这个样子的吗？”通过课件操作，对这个小正方形进行切分与组合，感受面积度量中的“运动不变性”——都是同一个小正方形变化而来的，转回来还是这个正方形（如图4）。

最后，以“面积为8”的多个图形设计来承上启下，以学习单的形式组织学生独立思考、分析判断，进一步深化对面积的感知（如图5）。先请学生对题中的3个选项进行表决，了解全班的认知情况，再进行有针对性的交流，丰富数图形面积的策略——割补。

通过设计一系列递进性的教学活动，使学生的认知不断走向深入：图3的设计既与前面的教学内容相衔接，又很好地融合第3个教材情境问题串中的问题“在方格中画3个不同的图形，使它们的面积都等于7个方格的面积”。图4着眼于对所添加小正方形面积“1”的考量，感受“1”的多变与不变，蕴含“分与合”的转化思想。图5以选择题的形式，考查学生对面积认知的综合应用，渗透空间想象力的培养——通过想象与推理，变不到1格的为1格，把不规则的变成规则，既发展了学生的量感，又获得空间观念、推理意识的提升。因此，通过关注数学核心素养的整体落实，以教学视野的广度、数学思维的厚度达到对教学支点方向的把握，可以使量感培养开出更芬芳的花、结出更丰硕的果。

（作者单位：福建省晋江市第二实验小学 福建省晋江市安海西隅小学）