体悟结构性内涵 实践迁移性学习

杨通文

【摘   要】数学教学着力于帮助学生建立知识结构，学会迁移性学习。教学“数一数有多少个三角形”习题时，教师在参考“教师用书”提供的解题思路基础上，结合学生实际情况提出另一种解题思路，并对两种思路进行比较，得出教学应“关注认知结构，在对比中理解、关联”“基于数学表达，在交流中理解、建构”“通过问题解决，发展数学思考力”。

【关键词】结构性内涵;迁移性学习;小学数学

人教版教材四年级下册第70页，有这样一道练习题（如图1）。

本题是一道拓展题，本题的解决可以体现出不同的思维层次：（1）解决数三角形个数的问题;（2）沟通“数线段问题”与“数三角形问题”的内在联系;（3）建立解决“数三角形个数”问题的数学模型。

在本内容的教学中，教师要着重引导学生感受数学知识的结构，学会迁移性学习，要关注学生的前概念生长、发展，让学生在结构性的素材中体会知识间的关联。

一、教学用书的解题思路

教材配套的《教师教学用书》中建议：教学本题时要在计数中培养学生有序思考的能力，并呈现了两种问题解决的方法。

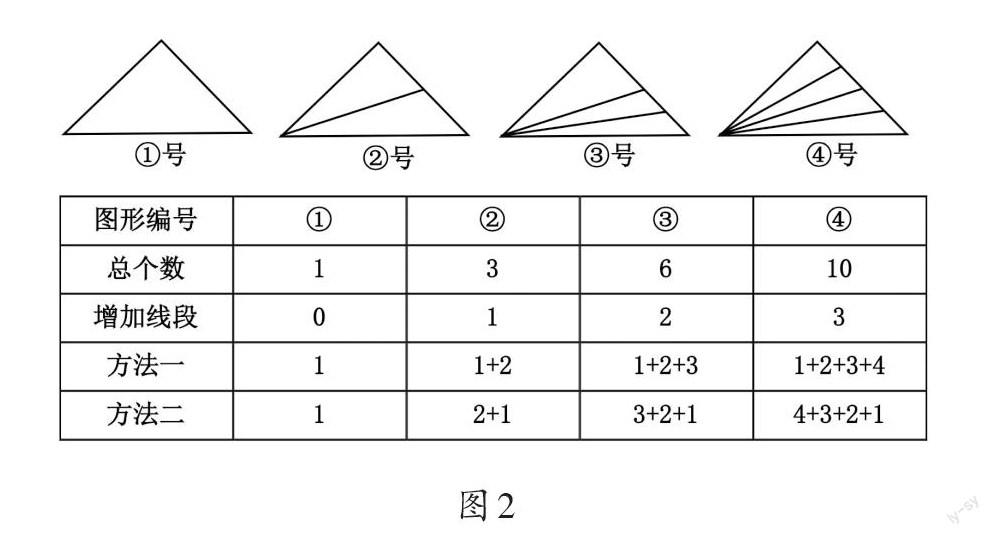
方法1：先让学生数出每幅图中的三角形个数，然后列表格进行整理，再仔细观察表格，自主发现规律。其规律为三角形内每增加1条线段，三角形的总数随之有规律地增加（如图2）。此方法重在引领学生学会用数学的眼光观察，用数学的思维发现，用数学的规律表达。

方法2：结合图形，有规律地一一列举三角形的个数，并将所有单个三角形、组合三角形的个数全部有序地数出来，对应分层记录，发现其规律为：所有三角形个数=单个三角形个数+2个单个三角形组成的三角形个数+3个单个三角形组成的三角形个数+……如④号图形，单个三角形的个数是4，其三角形的总个数为4+3+2+1=10（个）。此方法重在引领学生经历不重复、不遗漏的数三角形个数的过程，发展其有序思维。

《教师教学用书》提供的两种方法都能解决问题，体现了方法的多样性、思维的灵活性。

二、另一解题思路

学习需要基于学习者的原有经验。我校学生的学习基础相对薄弱，但正因如此，他们更需要教师帮助其理清知识结构，学会迁移性学习。按照《教师教学用书》介绍的方法进行教学，脱离我校学生原有的知识经验，缺乏对引导学生“用联系的眼光看待问题”“用结构的思维思考问题”的关注。因此，笔者结合学情及对结构性思维、迁移性学习的理解，提出另一种解题思路，让学生在数、记三角形个数的探究过程中，既能提升有序思考的能力，又能自主发现数学知识间的结构性关联。

具體操作时，教师可先引导学生从已有的知识经验出发，回忆数线段条数的规律，将数线段条数的方法、经验“嫁接”到数三角形的个数上。再引导学生观察三角形个数与线段条数之间的关系，通过列表、观察、思考、交流，发现属于自己的数三角形个数的规律。具体过程如下。

第一步：数线段的条数。

引导学生回忆数线段的方法及规律，以问题“三角形BC边有有多少条线段”促进学习真实发生（如图3）。

学生再次复习、巩固前概念，如将第四个三角形的BC边看作一条线段，那么，以B为起点，有线段BE、BD、BF、BC（4条）;以E为起点，有线段ED、EF、EC（3条）;以D为起点，有线段DF、DC（2条）;以F为起点，有线段FC（1条），共有线段4+3+2+1=10（条）。继而得出数线段条数之和的规律：线段总条数=线段上的总点数减1+线段上的总点数减2+……1。也可以记成：线段总条数=1+2+3+4+…（n-1）（n为总点数）。

第二步：找三角形的个数。

教师创设问题“你能根据数线段的规律找出三角形的个数吗”，引导学生发现三角形的个数变化规律与线段条数的变化规律之间具有一致性。以第二个三角形为例，在BC边上，增加一个点D，就在BC边上新增加2条线段（BD、DC），这两条线段与不变的A点围成了2个三角形（三角形ABD、三角形ADC），因此三角形总数也增加了2……由此得出数前图所示的三角形个数问题可以转化为数线段的问题加以解决。

以上过程体现了知识的结构性，提升了学生进行迁移性学习的能力。

三、两种思路的比较与思考

为了深入探究数三角形个数的问题，笔者将自己的解题思路与配套的《教师教学用书》解题思路进行教学对比，以改进教学。

（一）关注认知结构，在对比中理解、关联

认知心理学认为，学习资源的碎片化不利于学生的理解与记忆。教师不能简单地忽视学生的认知起点，忽视学生原有的知识经验。学习资源的结构化设计与呈现，有利于学生对知识进行感悟、观察、理解、交流、归纳，更有利于学生进行数学模型构建。笔者引领学生将从数线段的条数中发现的规律应用于数三角形的个数中，发现两者之间的关系，体现数学学习循序渐进、螺旋上升等特点，同时也让学生在具体的问题解决中感悟知识能力迁移的魅力;体会数学基本经验的一致性，感受学数学的好玩、有趣。

当然，不同教学思路之间也有相似之处。如无论用怎样的思路进行教学，学生都需运用结构化的表格梳理相关信息，借助数形结合的方式发现规律，并用“数或式”表示发现的结果。无论用怎样的思路进行教学都重视让学生在观察、交流、思考的过程中自主发现“数三角形个数”问题中的规律。教学过程始终凸显数与形的关系，让学生从不同视角思考各个量与式之间的关联，感悟“变中不变”的基本思想。

（二）基于数学表达，在交流中理解、建构

《义务教育数学课程标准（2022年版）》提出：“数学为人们提供了一种描述与交流现实世界的表达方式。通过数学的语言，可以简约、精确地描述自然现象、科学情境和日常生活中的数量关系与空间形式;能够在现实生活与其他学科中构建普适的数学模型，表达和解决问题。”以上两种教学思路都做到了将观察“形”、用“数或式”表示、学生表达三者有机结合，让学生基于个体的观察、归纳、发现，用数学语言交流自己的“再认识”，用[1+2+3+4+…（n-1）（n为总点数）]表达规律的一般性，用数学的方式精准地描述三角形个数。

（三）通过问题解决，发展数学思想、能力

数学教学不能仅关注问题的解决，更要关注在问题解决的过程中，学生数学思想的形成、数学方法的提升、基本活动经验的积累和运用。案例中，教师引导学生有序找线段的条数、有序数三角形的个数，让学生在观察“形”、用“数或式”表示以及表达的过程中学会观察、学会思考、学会表达，以问题解决为载体，以发现规律为核心，培育学生的模型意识。希望有一天学生走出校门，虽然遗忘了数学知识，但仍能用数学思想、数学方法、基本经验去思考问题、理解世界、表达认知。

（贵州省铜仁市印江县新寨镇中心完全小学555213）