小学数学运算能力培养策略的思考

吴炜

[摘  要] 培养和发展学生的运算能力，得从小学计算教学抓起。教学中教师应注重学习引领、习惯培养等，既要重视计算中算法、算理的同步引领，更要关注数学思维的培养，以及梳理、反思、提炼等学习意识的训练，让学生学得好习惯，助推运算能力的平稳发展。

[关键词] 算法;算理;思维;习惯;能力

运算能力是《义务教育数学课程标准（2011年版）》中明确的十大数学素养之一。它有简单的一面，在学生眼中仅是计算而已;也有深刻的一面，在学生眼中不仅是简单计算，还包括灵活计算和简便计算等。其实学生的见解也不尽然，运算能力还有更为理性的一面，那就是对算理详细阐述、缜密思维的过程，以及创新的、灵活的算法等。因此，在小学数学教学中，教师应把培养学生的运算能力放在重中之重的位置上去谋划，引导学生在合适的问题情境中学会分析、学会思考，从而更精准地理解算理，掌握算法，促进有序思考生成，进而助推运算能力的稳健发展。本文以苏教版三年级上册“两、三位数乘一位数的笔算（连续进位乘法）”为例，谈谈在小学数学教学中如何培养学生的运算能力。

[?]一、整合运算任务，算法算理兼修

对于小学生运算能力的培养，要算法、算理兼顾。因为知晓算法是基础，领悟算理才是根本，所以在每一节计算教学课中，教师的任务是多维的，既要让学生在真切的学习体验中掌握算法，又要让他们在学习中深刻领悟算理，最终实现运算能力的发展。

教学中，教师需要精准解读知识编排体系，明白学生的学习基础，从而引导学生在计算学习中实现经验的累加与思维的发展。首先，解读学习基础。通过对主题图的观察分析与思考，学生基本都能列出算式，部分学生还能依据已有经验、思维去计算算式。因为学生已经有了两、三位数乘一位数的学习积累，知道不进位笔算和一次进位笔算的算法，也明白其中的算理，所以他们跳一跳（稍加努力），有可能摘到果子。但是，教师也要清醒地看到，这部分学生的计算虽然没有困难，也就是说，他们能够运用思维迁移、经验类推等进行计算，但离真正领悟两、三位数乘一位数（连续进位）还有一段距离。其次，引导学习对比。为強化经验迁移、思维迁移，学生需要在复习上下足功夫。一方面教师指导学生复习不进位乘法，让学生计算如“12×4，3×32，2×312”等时唤醒其对算法的记忆，掌握乘法的算理;另一方面让学生在变化中感受算法的相通性，理解算理的差异。如把上述习题改编成“16×4，3×42，2×317”。最后出示教材中的例题7，让学生在读图、思考中得出算式48×4。面对该计算题，教师的第一要务不是指导，而是放手，让学生尝试练习。“这个题目和我们刚才复习的例题很像，大家想不想动手试试？”

用复习的杠杆撬动算法、算理，是发展学生运算能力的重要举措，也是培养学生有序思考的重要途径。因此，计算教学中教师应不厌其烦地让学生多说算法与算理，在述说中理清思路，在叙述中学会有序分析。

[?]二、组织运算活动，思考提炼兼行

培养学生的运算能力不是一朝一夕所能达成的，更不是一蹴而就的。因此，教师得学会耐心地做好计算教学事务，让学生在真切的计算学习与练习中学会思考，发展数感，进而提高学生的运算能力。同时，教师还得重视计算习惯的培育，让学生随着学习时间的延长，能养成良好的计算习惯。

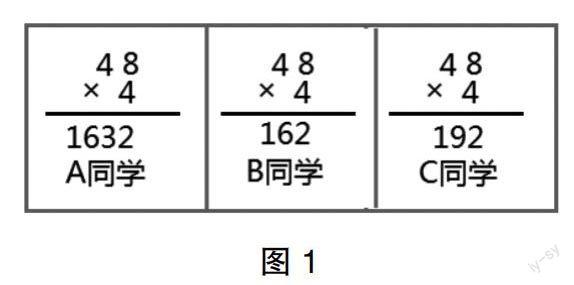
接着上面的案例思考：首先，组织展示活动。一是巡视学生自主练习情况，其间教师能够感知学生的计算状况，为选择代表性的素材提供储备;二是遴选出代表性的学生练习（见图1），以此作为新的学习研究素材，让学生在生成性的资源比对中感知算法、感悟算理。其次，引导学习争辩。考量学生自我的学习材料，既让学生体会到数学学习不是空中楼阁，而是源于他们自己的学习;又让他们在争辩中理清计算的算法与算理的差异，体会算法的相通性与算理的独特性。一是展示三个学生的学习成果，教师引导学生进行观察、分析、思考。这主要考量学生用自己的理解去解读三个计算结果，从而使自己的经验、思维在学习中产生碰撞。二是引发学习思辨，“仔细观察，结合自己的计算，谈谈你对这三位同学计算过程的认识。”观察比较后，有学生说：“C同学的计算是正确的，因为计算48×4，先算8×4=32，再算40×4=160，最后算160+32=192。”也有学生说：“A同学的计算错了，因为48×4比50×4=200小，而他算出来的结果是1632，所以是错误的。”还有学生说：“B同学的计算也是不对的，因为48×4的积一定大于40×4，也就是一定大于160，且小于200。”此时有学生产生了疑问：“B同学的结果是164，不是大于160小于200吗？”“是啊！那该怎么解释呢？”面对学生的质疑，组织学生争辩，学生最终弄明白了问题的症结所在：8×4是32，应该在个位上写下2，同时往十位上进3，而B同学没有在十位上加上这个3，所以是错误的。三是实施追问，让学生在问中感悟算理，强化数感。在学生研究分析、思考辩论的基础上，教师还得切实做好学习的引领者，应设计系列问题助推思考。“为什么C同学的计算是对的，十位上的9 是怎么来的？百位上的1又是什么意思？”让学生在问题的启发下再度思考这三位同学的解答，在思考中助推他们更精准地辨别计算方法的合理性，更深刻地理解算理。同样，教师的问也是一种示范，学生会在教师的不断追问中学习模仿，从而在学习中学着问自己，“应该怎么做？为什么要这样做？”由此促进他们深入思考学习，在不断追问中更好地发展他们的计算能力，最终掌握算理。

从中能够看出，给予学生应有的信任，他们就会认真思考、细心比较，也一定能掌握好算法，理解透算理。案例中截取的几组具有代表性的发言，让教师感受到学生数学学习的能动性，以及学生数学学习的智慧。比如，学生自主的估算学习体现了估算意识已经在他们的脑海中生根发芽。又比如，计算304×7时，一位学生算出的结果是238。此时，教师抓住这一契机，利用好这一错误资源，再度引导学生反思学习：“这位同学的问题出在哪里？”在前面争辩学习活动经验的基础上，学生很容易看出：304×7一定大于300×7=2100，而238这个答案与2100相差太多。教师引导学生再一次进行自主练习与交流分析，从而让算法得到巩固，算理得以升华。与此同时，学生的数感也在学习中得到发展。

由上述案例可知，有效的数学教学应贴近学生的思维进行。教师引领学生做一个倾听者，让学生在倾听中开阔数学视野，在倾听中实现思维碰撞，进而学会思考，增强数感。

[?]三、创新运算训练，梳理反思兼顾

“少成若天性，习惯如自然”，小学生的数学学习亦如此。要培养学生的运算能力，教师应在教学实践中培养他们良好的数学学习习惯，尤其是梳理学习的习惯和反思学习的习惯。教师指导学生不断梳理两、三位数乘一位数的学习历程，反思学习中的失败教训，总结学习顺利的心得等，久而久之，学生定会生成好的学习习惯，也会将计算的算理深植于心。

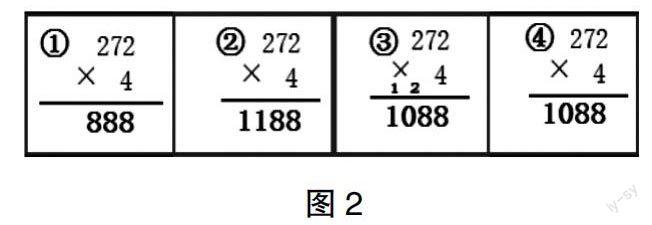
例如，在例题7的“试一试”部分教学中，教师就得学会放手，让学生运用这一阶段学习的经验、思维、技能等去尝试练习，从而在学习中体会难度增大的三位数乘一位数（连续进位）的计算方法。让学生在试做中发现学习的不足，在反思中促进习惯养成，加深对三位数乘一位数算理的理解。一是组织自主试做。让学生独立完成“试一试”中的272×4，教师巡视，察看学生的学习状态。二是组织学习展示。教师选取具有代表性的几个案例（见图2），通过展示引发学习争论。有学生说：“①是错误的，他没有注意十位上7×4是28，应该在十位上写上8 ，还得在百位上进2。”有学生评价：“②也是错误的，他记住了进位，但是应该进2，而不是进3，所以错了。”还有学生说：“③④都是正确的。”此时，就有学生反驳道：“他们答案都是对的，但我认为③的做法更好，你看他把十位上进的2、百位上进的1都写出来了，非常清晰。”“这位同学的观察很仔细，分析很透彻，值得我们学习。同时，我们还得向③号同学学习，细心做题，不要忘掉任何一个小细节。因为细节决定成败。”教师及时追评，既肯定了学习活动的成效，又能帮助学生学习好习惯，养成好本领。

从中可以看出，计算教学中教师应重视好习惯的养成教育，引导学生写好进位，字迹工整，数位对齐，以及读清符号、读准数字、仔细验算等，从而让学生的数学学习习惯的培养落实在每一处细节，以达成“心中有算理，笔头落习惯”的理性境地。

在这节课的教学反思中，笔者深深地体会到计算教学不简单，也不那么单薄，因为计算教学的背后是一批性格特点各异、行为习惯不同的学生，他们对计算的思考有很多的随意性，对算法的掌握、算理的理解稍欠火候，计算方面习惯的养成有很大的发展空间，数感的培养还在不断生长。因此，小学数学教学中教师需学会贴着学生的思维去施教，贴着他们的想法去引导，从而让他们的思维活跃起来、灵动起来，碰撞思维火花，掀起头脑风暴，深刻领悟运算的算理、规律等，助力运算能力的穩步前进与有序发展。