走出概念教学的误区

毛国荣

［摘 要］概念是最基本的数学知识，也是建立数学逻辑的基石，可以说任何数学问题都是以数学概念为基本元素的，也可以说一切数学问题都是对概念的研究和拓展。对原始概念的牢固掌握，直接关系到学生日后对建立在这个概念上或者与这个概念有关的一切数学规律的推导，同时，也关系到学生解题能力的提高。当学生对数学规律和实际问题的掌握变得熟练后，其对数学学习的兴趣自然大大增强。

［关键词］概念；误区；规律；对比

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）32-0049-03

近年来，针对概念教学的教研活动愈加频繁，不少一线教师进行了坚持不懈的努力，也做出了艰苦的探索，总体来说有所进展。然而，一些重大关切的命题仍没有取得突破性进展，如只重视通过直观操作的过程和结果来概括规律，却没有从理论逻辑上真正推演；只习惯于用顺向的“示例总结——规律方法”，却很难见到用逆向的“规律方法——举例说明”；只片面注重对概念的剖析，却缺乏对相关概念横向的对比勾连；只重视与概念有关的生活情境，却很少将其他数学知识引进概念中，缺乏知识板块的互融互通。本文就这四大误区进行集中整理总结，并从理论上寻求破解之道。

一、只重操作，忽视理论

小学数学概念的形成过程至关重要，而一旦需要展示概念的形成过程，直观演示便是首选，由此，动手操作就理所当然成了热门。但凡事过犹不及，如果只是片面追求动手操作，企图从操作过程和结果中总结规律，而不从理论逻辑上推演，势必会让概念解读变得表象化。这样一来，学生只会对概念断章取义，形成教条主义，进而丧失理性的逻辑推理能力。

例如，在教学“圆的性质”时，有教师安排了两个任务：①在圆形纸片上画出半径和直径；②通过折叠、测量，探索半径和直径的关系。学生经过直观操作后得出结论：①在同一个圆或者大小相等的圆中，半径（或直径）都相等；②任意一个圆中，直径和半径的数量都是无穷的；③在同一个圆或者大小相等的圆中，直径的长度都是半径的2倍。

教师的设计初衷，是让学生通过操作活动总结出圆的一系列性质。直观操作确实能让学生亲眼看出有关半径和直径的一些性质，但是操作的过程是流水式的，只训练了学生的双手，没有训练到大脑。因此，在操作活动中，教师要引导学生手脑并用，设计步骤驱动学生深入思考，以手动带动脑动。操作只是表象，思维才是核心，学生应该在操作中有所体悟。为此，笔者对任务做出如下改编。

【改编后】①重温圆的定义——当一条线段绕它的一个端点在平面内旋转一周，另一个端点的轨迹就是一个圆（也可换种表述）；②从定义出发，推理出圆应该具备什么基本性质。

这样一来，虽然取消了直观的操作，但是加深了学生对圆的概念理解，还促进了学生的自主探索，让学生从理论上探索圆的性质。

精彩的操作活动不能徒有其表，如果设计的操作只顾着让学生好玩，那学生就没有动脑思考的过程，也不会经历反思内省。改编后的任务，虽然没有任何操作活动，但却是紧扣圆的概念来设计的。有的数学活动脱离了直观，反而能够让学生集中精力专心致志地进行理论研究。如重温圆的定义时，学生可能会出现不同的表述，这代表了不同的理解方式，说明学生对概念理解不是死记硬背和机械复述。学生要做到言之有物、表达准确、直击关键，就必须先在心中对圆的概念有一个清晰的勾勒，默想出圆的所有要素和组织结构，只有这样，才能有话可说、言之凿凿。当学生按自己的意愿说出圆的概念后，教师让学生返回去推想圆的基本性质，就是对学生构想的一次检验和确认。学生会重新审视、回顾并构建圆的动态过程及几何原理，进而推出圆具备的所有性质。

二、只用顺向，难见逆向

出示范例的方法有两种。第一种是顺向的“示例总结——规律方法”，即先向学生提供大量相同或相似的实例，包括正例和反例，然后概括出它们的共同特征，最后抽象出一个概念。第二种则是逆向的“规律方法——举例说明”，即先给学生提出概念，然后呈现一些样本，最后让学生分辨和判断，哪些属于这个概念，哪些不属于这个概念。然而，在数学中，有些概念如果只采用第一種方法教学，那么学生是很难完全掌握的。

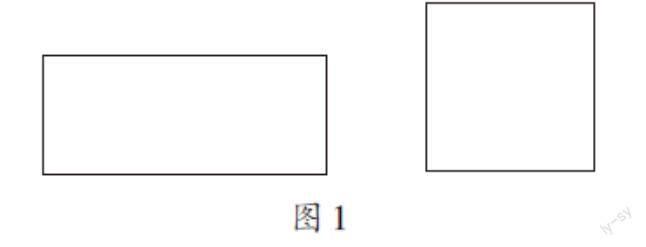
例如，在教学“面积”的概念时，教师通常会采用第一种顺向的方法，即先让学生观察并比较课本封面、桌面、黑板面、墙面，分出它们的大小，感受它们的存在形式，再让学生通过触摸对面积建立质感，最后归纳出面积的概念。按照这种教法，教师安排了两个任务：①对比图1中两个图形面积的大小；②两个图形的面积分别指哪些部分？请用涂色表示。调查结果：全班49人，只有23人做对，正确率为46.9 %。

为什么这样一道基础题，却有超过一半的人做错呢？学生体验多了，材料也丰富了，为什么还是会将面积与周长混淆？究其根本，是因为学生没有深入领会面积是图形内部包含的所有区域，而不是边缘的扩张程度。笔者认为，当多数示例的特征与指向概念的内涵难以达到吻合时，教师就要直接摒弃第一种方法，转而启用第二种方法，如果实在难以取舍，那就折中处理，将两种方法融合。为此，笔者将任务进行了如下改编。

【改编后】①让学生口述面积的概念（表述不清时，可以打开教材参考）；②描述一下指定物体的表面或者图形的面积是指哪一部分？③通过对比辨析，严格区分面积和周长的界线。

如此一来，不仅能让学生明白面积到底是指哪部分，还能与周长区分开来，加深了学生对面积的独特印象，突出了生本教育理念。

面积和周长经常被混淆，如果仅从大量示例中归纳出面积概念，是无法避开周长概念的负迁移的。因为在一系列面积的示例中总是伴随着周长的影子，所以学生在触摸面积大小时，总会在潜意识里注意到周长的存在，而且通过触觉感知和抽象归纳得出的概念具有很强的模糊性，学生停留在一种似是而非、模棱两可的意识状态，具体也说不上什么是面积，导致一旦出现干扰条件，就立马出错的现象。改进后的任务，让学生直接陈述面积概念，从内涵上理解概念本质，即先借助对概念的理性认知，按图索骥来寻找概念的外延——生活中物体的表面，然后再观察和探究面积的实例，此时学生对面积概念有了一个全面且深入的把握，最后区分周长和面积就正合时宜。

三、只重剖析，不知对比

一般而言，每个概念呈现后，都有一个解读环节。目前的现狀是，不少概念课只关注概念本身，忽视呈现与概念有横向联系的其他概念。

例如，在教学体积的概念时，有教师设计了如下教学片段。

师：请回顾“物体所占空间的大小，叫作物体的体积”这个定义，关键词是什么？

生1：物体、空间、大小。

（教师按照学生说的圈出关键词，学生朗读，接着教师出示教材习题）

师：①一团橡皮泥，先捏成长方体，再捏成球，两种物体哪个体积大？哪个体积小？②用枚数相等的1元硬币堆叠成不同形状（如图2），哪个体积大？请说出你的理由。

上述片段中，就对体积的理解方式而言，太拘泥于概念的文本含义，翻来覆去就是那几个词，缺乏横向比较。这样教学概念，略显苍白无力，也会导致学生对概念结构的理解停滞不前，甚至会越听越糊涂，越听越麻木。教师应该帮助学生建立概念之间的横向联系，让学生通过横向对比寻找各个概念之间的异同，再通过对比辨析，加深对目标概念的精准定义。当学生深刻掌握新概念之后，教师又可以将新概念反过来衬托旧概念，即将旧概念回炉重温，从而拓宽学生的视野，让学生将所有相关概念尽收眼底，连成知识网，构建系统认识。为此，笔者在上述任务的基础上，增加了新的内容。

【增加习题】③有人说：“立体图形中体积与表面积的关系，就像平面图形中面积与周长的关系。”你同意这种说法吗？请用文字或图画说明你的理由。

通过研究，学生感悟到，周长是平面图形边界的长度；面积是边界内部容纳的范围；表面积是物体外表的伸张程度；体积是物体表面包含的空间范围。如理解体积单位1立方厘米时，除了寻找对应的实物，学生还应将长度单位1厘米与面积单位1平方厘米拿来比较（如图3），当然，这种比较也可延后至学习了长方体的体积之后。这样的学习，可以让学生领会从长度到面积再到体积的变化是一个维度的不断演变升级的过程，同时也能科学地解释各单位的名称制定，如为何面积单位是长度单位加“平方”前缀，而体积单位则是加“立方”前缀。

如果对概念的理解仅仅拘泥于目标概念，那么学生的眼界就会非常狭隘，思维也会陷入定式，看问题就会片面而肤浅。如体积概念，其实简简单单一句话就可以将概念说清楚，但是这个概念又很深邃，不是随随便便透过字面意思就可以理解透彻的。此时，如果教师能够将体积、长度和面积概念进行横向对比，那么学生理解概念的站位和角度就会大大提高，眼界开阔了，视野拓宽了，看问题自然就能全面深入。不仅如此，由于长度、面积、体积之间的维度关系，学生在理解体积概念时会自动与长度和面积概念进行对比，这样一来，学生对体积概念的把握就会更加精准和严谨。

四、只重联系生活，不知联系其他知识

“数学从生活中来，又到生活中去。”数学的确来自生活，因为学生需要靠形象思维来理解数学；数学的确也可以应用于生活，因为学生需要在应用中找到数学的价值和存在感。这句话的本意没错，但是数学更应该是思维的工具，是一切科学的理论工具。

例如，在教学“比的认识”时，为了让学生感受到“比”的实用性以及比与现实联系的密切性，有教师设计了如下教学过程：①让学生观察并研究5张画像的协调性（图略，其中有3张画像的长与宽之比相同）；②让学生根据行程问题、计价问题引出比的概念；③让学生根据图片叙述奶茶的甜度与含糖量，引出奶茶质量和所含糖量的比；④让学生通过测量影长推测树高的实践活动；⑤师生一起归纳“比”的定义。

小结学习比的作用时，有的学生说“比”可以解决画像协调与否的问题，有的学生说“比”可以用来间接测量旗杆、烟囱、信号塔等高大建筑物的高度……学习“比”如果只局限于眼前的生活，看似是应用知识服务生活，其实与课程标准倡导的“应用意识”背道而驰。“比”的巨大价值在于简化和异化其他数学概念，如比和分数的关系、比与除法的关系。比可以对分数和除法的重合定义进行异化、扩充和弥补，分数和除法不能解决的问题，用比可以解决；分数和除法不便解释的问题，用比可以解释清楚。比不但可以表示除法运算以及部分与整体的配额情况，还可以表示两个量的倍数关系和不同类量的比较关系。事实上，不同类的两个量的关系在除法定义和分数定义上都站不住脚，而引进比的概念，就可以打破这个壁垒。其实，比的价值远不止于此，小学阶段的“比”其实还是“函数”的雏形。

数学概念的教学如果只是让学生了解并记住概念，囫囵吞枣不加消化，那么完全可以只对文本进行肤浅解读，再举几个示例就完成教学。然而，在这样的教学模式下，学生对概念的理解是僵化且呆板的，一旦在练习中遇到稍复杂的题型，学生就会束手无策，因此，概念教学应该开阔思路、创新方法。

［ 参 考 文 献 ］

[1] 王芳.小学数学概念教学真实场景设计策略[J].新教育，2021（29）：42-43.

[2] 张晶.互联网思维下的小学数学概念教学：以“分数”的教学为例[J].江苏教育，2021（61）：42-45.

[3] 郑桂斌，李静.基于学生理解水平的小学数学概念教学模式探究[J].辽宁教育，2021（17）：83-85.

（责编 李琪琦）