挖掘知识点，培养学生核心素养

葛卫国 刘岳

一、教材分析

数学教材的编排是递进式的，知识点在教材中是有纵横联系的。例如，“补角”这节内容，学生是在学习过直角、平角的基础上，再通过一定的数量关系和图形关系学习两角互余、互补的概念、性质，以及用方程的思想来解决某个角的度数的问题，为以后研究角相等做好铺垫。《义务教育数学课程标准（2022年版）》对补角的要求是：理解补角的概念，探索补角的性质，会求一个角的补角。

教师在研读教材时，必须找准重点、难点和关键点，才能在教学过程中突出重点，解剖难点，找到突破点，否则会影响教学效果。本节课的重点、难点就是补角的概念和性质，关键点就是数形结合。

二、教学过程

1.情境引入，激发思维

师：我们已经学习过角、直角、平角、余角，大家回忆一下，什么叫作互为余角？如果我在直角里画一条射线，那么形成的两个角有什么数量关系？如果我在平角里画一条射线，那么形成的两个角存在什么样的数量关系？

设计意图：从学生已有的知识或者身边的生活常识出发，让学生通过类比联想，触类旁通，不知不觉地进入学习新知识的情境中。教师通过将图形关系转化成数量关系，让学生明确事物之间是相互联系、相互转化的，体现数形结合的思想。

2.探究新知，发展思维

活动1：识补角

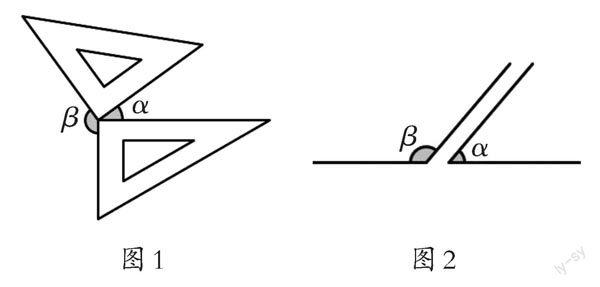
（1）在图1、图2中，∠α+∠β=。

（2）在A组中有10°、55°、75°、100°、145°的角，在B组中有35°、80°、105°、125°、170°的角，对A组中的每一个角，请在B组中找出它的补角。

（3）一个平角，从角的顶点画出两条射线，形成三个角，分别标上∠1、∠2、∠3，那么∠1、∠2、∠3互为补角吗？为什么？

设计意图：教师通过例题初步让学生认识补角的概念，强化余角和补角的区别，认识互余和互补两个角之间的大小关系。通过计算，学生再次加深对余角、补角的认识。

活动2：求性质

（1）余角有何性质？模仿余角性质，请猜想一下补角的性质。

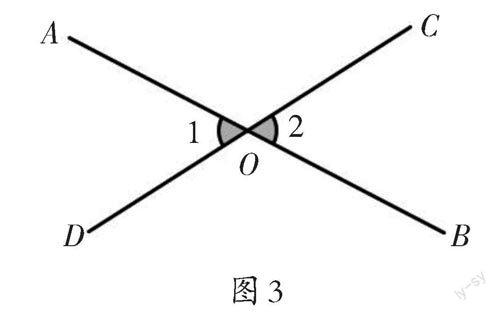
（2）如图3，利用补角概念，求证：∠1=∠2。

（3）若∠1+∠2=180°，∠3+∠4=180°，且∠1=∠3，那么∠2与∠4有什么数量关系？

设计意图：猜想也是数学思考的一种方法。由类比猜想到验证猜想，增强了学生自信心，也为新学知识打下良好的基础。（2）（3）是由教材内容改编而来，对学生更有吸引力和挑战性。学生在探索互余的性质后，类比迁移互补的概念及性质，很容易得出补角的两个性质：同角的补角相等；等角的补角相等。教师通过这两个性质引导学生用数学语言表达思考过程，并归纳性质，培养学生由具体问题到抽象出几何命题的能力以及语言表达的能力，使学生养成类比质疑的好习惯，让学生在学习、讨论中不断地发现问题、解决问题，从而认识事物的本质。

活动3：找补角

（1）一副三角板如图4放置，请找出∠DAC的补角。

（2）如图5，点O在直线AB上，∠AOC=30°，将一个含有30°角的直角三角尺的直角顶点放在点O处，较长的直角边OM在射线OB上，较短的直角边ON在直线AB的下方。图中与∠BOC互补的角有 。

设计意图：找一个角的补角，学生往往认为补角就是钝角旁边的角，却忘记了只要两个角的和加起来等于180度时，两个角就互为补角。教师通过此活动再次强化学生对补角概念的理解，让学生深刻掌握互补是两个角之间的关系，与位置无关。

活动4：测补角

要测量两堵墙所形成的∠AOB的度数（如图6），而且不可入内测量，该如何测量？

设计意图：在测量补角时，有的学生眼光只放在∠AOB的内部，无法得出结论。因此，教师要引导学生采用间接的方法，测量∠AOB的补角。（∠AOB的补角有两个，它们是对顶角，测量任意一个都行，拓展学生的思维。）同时，教师要检查学生使用量角器的方法是否正确。

活动5：算补角

已知一个锐角的补角等于这个锐角的余角的3倍，求这个锐角和它的补角。

设计意图：学生用方程求解的前提是正确认识余角和补角之间的关系，抓住关键词和关键句，列出方程再求解。

3.归纳方法，聚焦思想

师：解决补角问题的基本思路是什么？本专题涉及的数学思想方法有哪些？

设计意图：教师通过提问的方式，让学生自己总结解决补角问题的基本思想，再延伸到整节课涉及的数学思想方法。教师最后总结——在学习补角的概念中，用到了类比思想，在解答时用到了数形结合思想、分类讨论思想、方程思想等。这些数学思想，是帮助学生解决问题的常用思想，而正确画出图形，是学生运用这些思想的最好桥梁。

三、教学反思

1.追求素养化课堂

在课堂教学中，教师要精选学科核心知识作为教学载体，根据知识属性匹配课堂培育目标，帮助学生发展核心素养。因此，教师应该在深度解读教材的基础上，根据学生基本情况，对教材中的内容及呈现方式进行再重组、再优化，让教材能更好地为教学服务，为学生服务。值得注意的是，深度解读教材，不是指把课本内容拓宽加深后变得繁、难、偏、怪，而是要把课本没有说完、说全的内容，通过钻研把知识点讲到位，讲到边，讲得深刻，讲得有味。

2.凸顯知识的完整性和递进性

数学中每节知识点看似是独立的，实际是有关联的。每一节知识内部都存在逻辑关系以及完整性，我们不能把单元知识讲解得支离破碎，而要让知识形成完整体系。例如，“补角”这节内容，从概念到性质，再到运用，层层递进，逐步展开，概念是起点，性质是升华，运用是高潮，凸显了知识的递进性。

3.发挥学生学习的主动性和智慧性

课堂上，教师要鼓励学生各抒己见，发表创造性意见，营造良好的互动氛围，让学生参与简单内容的讲解和整理，摆脱“一味听”的状态，主动参与到课堂中来，积极挖掘学生的智慧，不断增强探究的信心和能力，及时给予多元欣赏性评价，让学生有机会“青出于蓝而胜于蓝”。

4.深度挖掘知识点中蕴含的思想方法

数学教学的目的，不是知识的本身，而是解决这类问题的方法。任何人都不可能把全部的数学题做完，也无法做完。虽然解题思路和解题方法不尽相同，但万变不离其宗。教师只有引导学生找出知识点背后隐含的数学思想方法，才能不断地发展学生的思维能力。

（作者单位：1.江苏省泗阳县教师发展中心； 2.江苏省泗阳县树强中学）

本文系江苏省教育科学“十四五”规划2021年度课题（初中专项，编号E-c/2021/17）“聚焦学生思维：初中数学教师深度解读教材的实践研究 ”的阶段性研究成果。