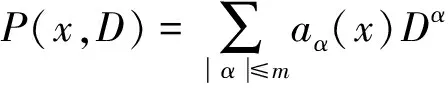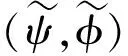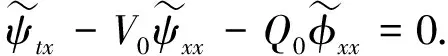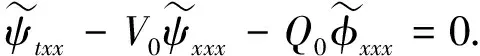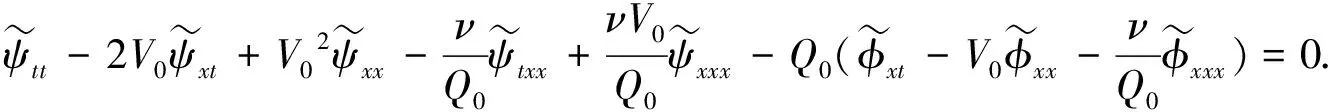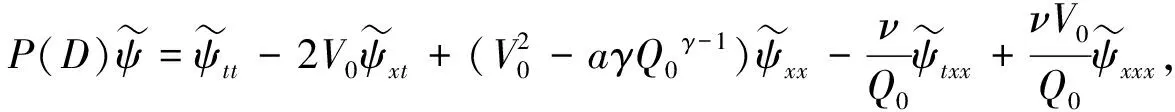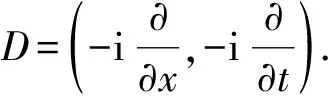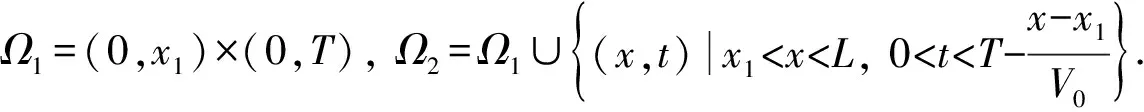一维线性化可压缩Navier-Stokes方程组的近似能控性
杜润梅, 吕晓娜
(长春工业大学 数学与统计学院, 长春 130012)
0 引 言
Navier-Stokes方程组是流体力学方程中描述黏性牛顿流体的方程. 一维的可压缩等熵Navier-Stokes方程组为
其中ρ(x,t)表示流体的密度,v(x,t)表示流体的速度, 正数ν表示流体的黏性,f表示质量源,g表示外力, 压力p满足p(ρ)=aργ,a>0,γ≥1.
目前, 关于可压缩Navier-Stokes方程组的性质研究已取得了很多成果[1-8].其中, 文献[5-6]研究了线性化可压缩Navier-Stokes方程组的一些可控性结果.本文考虑在常数稳态(Q0,V0)附近线性化的Navier-Stokes方程, 其中Q0>0,V0>0.先考虑如下初边值问题:
其中Q0>0,V0>0, (x,t)∈QT=(0,L)×(0,T),ω=(0,x1), 0 类似于文献[5]中定理2.3和文献[6]中命题2.1, 由半群理论可得系统(1)-(4)的适定性: 命题1对任意(σ0,u0)∈L2(0,L)×L2(0,L), 系统(1)-(4)存在唯一弱解(σ,u)∈X, 满足ut∈L2(0,T;H-1(0,L)), 其中 X=C([0,T];L2(0,L))×[L2(0,T;H01(0,L))∩C([0,T];L2(0,L))]. 令Z=L2(0,L)×L2(0,L), 在Z上定义其内积和范数分别为 在Z上, 方程组(1)-(4)的对偶问题为 下面给出对偶问题(9)-(12)的唯一延拓性: (13) 则有 由定理1, 可得对偶问题(5)-(8)的唯一延拓性: 由对偶问题(5)-(8)的唯一延拓性, 可得(1)-(4)的近似能控性: ‖(σ(x,T),u(x,T))-(σd(x),ud(x))‖L2(0,L)×L2(0,L)≤ε. 下面证明对偶问题(9)-(12)的唯一延拓性. 定义1设曲面S⊂N是C1的, 且曲面S在点x处的法向量为ξ.如果Pm(x,ξ)=0, 则称曲面S在点x处对于P(x,D)是特征的.如果曲面S在所有点处都是特征的, 则称曲面S为P(x,D)的特征曲面. 1) 设在分布意义下,Θ∈D′(Ω2)满足P(D)Θ=0且Θ(x)在Ω1上为0, 则Θ(x)在Ω2上也为0; 2) 每个与Ω2相交的P(D)的特征超平面一定与Ω1相交. (14) (15) 对式(15)中x求导, 得 (16) 由式(14)~(16), 得 即 (17) 把式(10)代入式(17), 得 (18) 定义算子 (19) 引理2P(D)的特征超平面是t=C1和t+x/V0=C2, 其中C1和C2都是常数. 证明: 假设Π={(x,t):ξx+ηt=C}是P(D)具有法向量(ξ,η)≠(0,0)的特征超平面.根据定义1, 可知 因此ξ=0或η=V0ξ.从而特征超平面Π的法向量是(0,1)和(1/V0,1).于是P(D)的特征超平面是t=C1和t+x/V0=C2.证毕. 下面证明定理1. 证毕.1 线性化系统的近似能控性
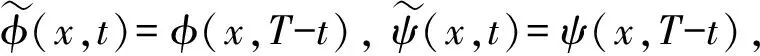
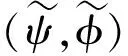
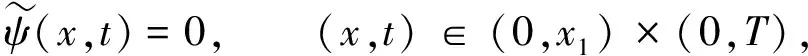
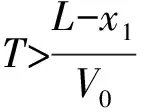
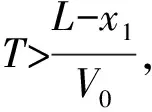
2 定理1的证明