四向穿梭车仓储系统的多订单任务调度优化

隋 振, 吴 涛, 唐志国, 张天星, 陈华锐

(吉林大学 通信工程学院, 长春 130012)

四向穿梭车仓储系统(four-way shuttle storage system)是在穿梭车仓储系统(shuttle storage system)的基础上发展而来的一种新型自动化立体仓库, 其主要由四向穿梭车、 导轨、 货物提升机和货架等构成. 四向穿梭车可以在自动化立体仓储巷道之间的导轨上向前、 后、 左、 右4个方向运动, 同时也可以利用仓库货架之间的货物提升机实现上下两个方向的垂直运动, 克服了穿梭车仓储系统中穿梭车只能在一个巷道中运动及穿梭车出现故障后该巷道的出入库作业无法正常进行的缺点, 提高了仓储的作业效率.

目前, 自动化立体仓储系统中相关的作业任务调度研究主要集中在堆垛机式立体仓库及自动导引车(AGV)系统, 已取得了许多研究成果. 余娜娜等[1]对自动化分拣仓库的AGV调度问题进行分析, 将完成作业任务的最短工作时间作为目标函数, 使AGV调度和路径规划综合在一起, 实现了自动引导小车的路径规划； 张丹露等[2]在A*算法的基础上, 提出了一种交通规则和预约表下的动态加权地图的改进算法, 解决了智能仓库多AGV协同调度问题； Fukunari[3]通过分析RGVs(rail-guided vehiclessy stem)系统的存取特点, 在交叉存取的基础上, 建立了RGV系统循环交叉存取时间模型, 使用排队论方法对该模型进行求解研究； 方彦军等[4]提出了一种改进的人工狼群算法, 有效解决了AGV系统复合作业三维空间的调度问题； Fanjul-Peyro等[5]为解决多AGV调度问题, 将其等价为无关并行机调度问题, 用精确算法对大规模问题求解； Malopolski[6]在拥有方形拓扑结构的多AGV运输系统中提出了一种防止冲突和死锁的方法； 刘二辉等[7]针对传统变异算子缺少启发式规则导致变异产生优质解概率较低的缺陷, 提出了一种改进遗传算法的AGV动态路径规划算法, 为增加改进遗传算法的局部寻优能力, 对每代的最优解都进行了模拟退火操作； Mousavi等[8]假设AGV在执行任务过程中不发生冲突, 提出了基于遗传算法和粒子群优化算法的混合算法解决调度问题. 目前的研究主要用粒子群优化算法[9]、 遗传算法[10-11]及多种群遗传算法[12-13]等解决AGV系统及堆垛机式立体库系统中单订单任务的调度问题, 对于仓储系统中同时对多个订单任务的调度研究文献报道较少.

基于此, 本文对四向穿梭车系统同时处理多个订单的作业任务进行研究, 建立系统的作业时间模型, 利用改进的遗传算法对模型求解. 首先, 针对模型特点设计一种包含多订单作业任务的作业顺序及货物提升机选择信息的染色体; 其次, 为解决遗传算法易陷入局部最优的问题, 对遗传算法的交叉概率和变异概率进行自适应设计, 并与模拟退火算法相融合组成自适应遗传退火算法; 最后, 利用实例验证自适应遗传退火算法求解的有效性, 并通过解码得到多个订单任务的作业顺序及货物提升机的选择信息.

1 问题描述及假设

1.1 问题描述

与传统的穿梭车仓储系统不同, 四向穿梭车仓储系统中的四向穿梭车可以前后左右运动, 四向穿梭车在执行跨层作业任务时需要规划水平运动和垂直运动, 其中水平运动可由四向穿梭车自己完成, 垂直运动需要四向穿梭车与货物提升机相互配合完成. 四向穿梭车系统布局如图1所示.

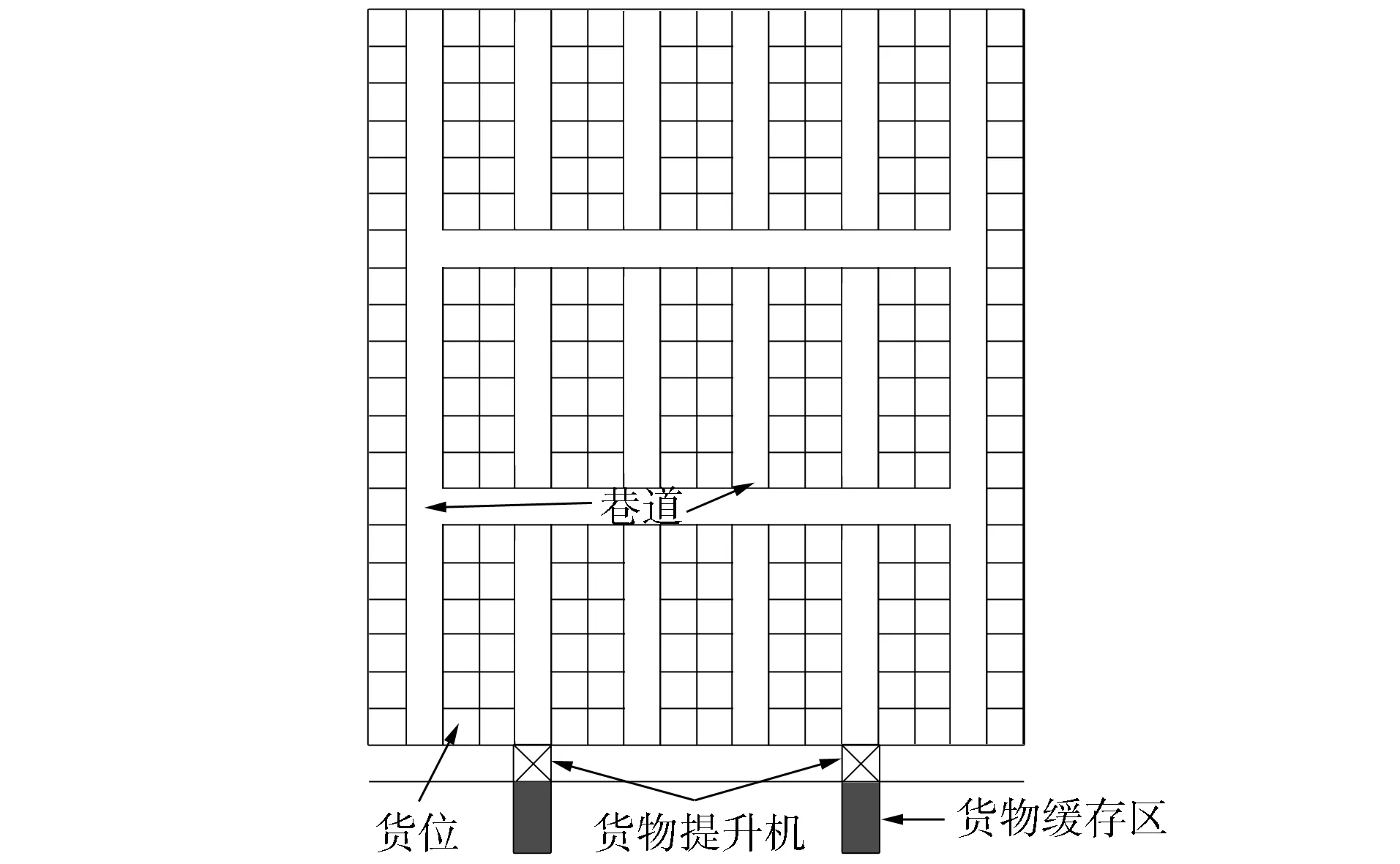
图1 四向穿梭车系统布局Fig.1 Four-way shuttle system layout

穿梭车仓储系统的作业任务包含出库作业、 入库作业和复合作业3种类型. 由于系统的3种作业类型原理基本相同, 因此本文主要研究四向穿梭车系统的出库作业任务. 对于跨层任务系统的出库作业任务主要分为两个环节： 1) 货物提升机运载四向穿梭车将其运送到出库货物所在层, 然后四向穿梭车运行到出库货物所在位置的轨道将货物取出； 2) 四向穿梭车将需要出库的货物运送到货物提升机缓存区, 然后货物提升机将运送货物的四向穿梭车运载到货架底层并释放提升机. 对于底层的出库任务则不需要货物提升机配合四向穿梭车进行作业.

因此, 该系统中四向穿梭车和货物提升机的匹配问题是决定出库作业任务效率的关键. 目前, 多数研究只针对单订单的任务调度情况, 而未考虑双订单同时到达时的任务调度情况. 在处理四向穿梭车系统运行中遇到双订单任务到达的情况时, 通常按照订单任务优先级优先处理一个订单任务. 所以, 研究四向穿梭车系统双订单作业任务的调度方案具有重要意义.

1.2 相关运行规则及假设

假设四向穿梭车系统中没有冲突、 阻塞发生, 为便于研究提出以下运行规则[4]：

1) 四向穿梭车每次只能运送一个货位的货物；

2) 每个货物提升机只能运载一个四向穿梭车；

3) 每两个相邻路径节点之间的导轨只能被一个四向穿梭车占用；

4) 每个四向穿梭车取完货物后, 在货物提升机缓存区等待货物提升机将其运送至底层；

5) 四向穿梭车和货物提升机在空载状态和满载状态下的运行速度及加速度相同；

6) 四向穿梭车之间没有冲突；

7) 忽略出库货物与空闲四向穿梭车在提升机货物缓存区的对接时间.

采用A*算法离线状态下计算出在每层货架中以货物提升机所在位置节点为起始点到出库货物所在货位节点为目标点的最短路径.

2 出库时间模型

本文采用G=(L,N,M)表示仓库中货物所在位置, 其中G为系统中货物所在货架的位置,L为货物所在的行数,N为货物所在的列数,M为货物所在层数.用

O≥F

(1)

表示系统中四向穿梭车的数量大于等于货物提升机的数量, 其中O为系统中的四向穿梭车数量,F为货物提升机数量.

设出库货物的坐标为(Lq,Nq,Mq), 对应的四向穿梭车在巷道中取货物时的坐标为(Lq,Nn,Mq), 货物提升机的坐标为(Lf,Nf,Mf), 则货物坐标中Nq与相邻巷道坐标中Nn之间的关系为

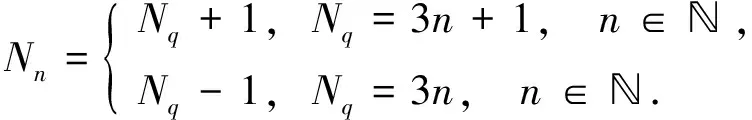
(2)

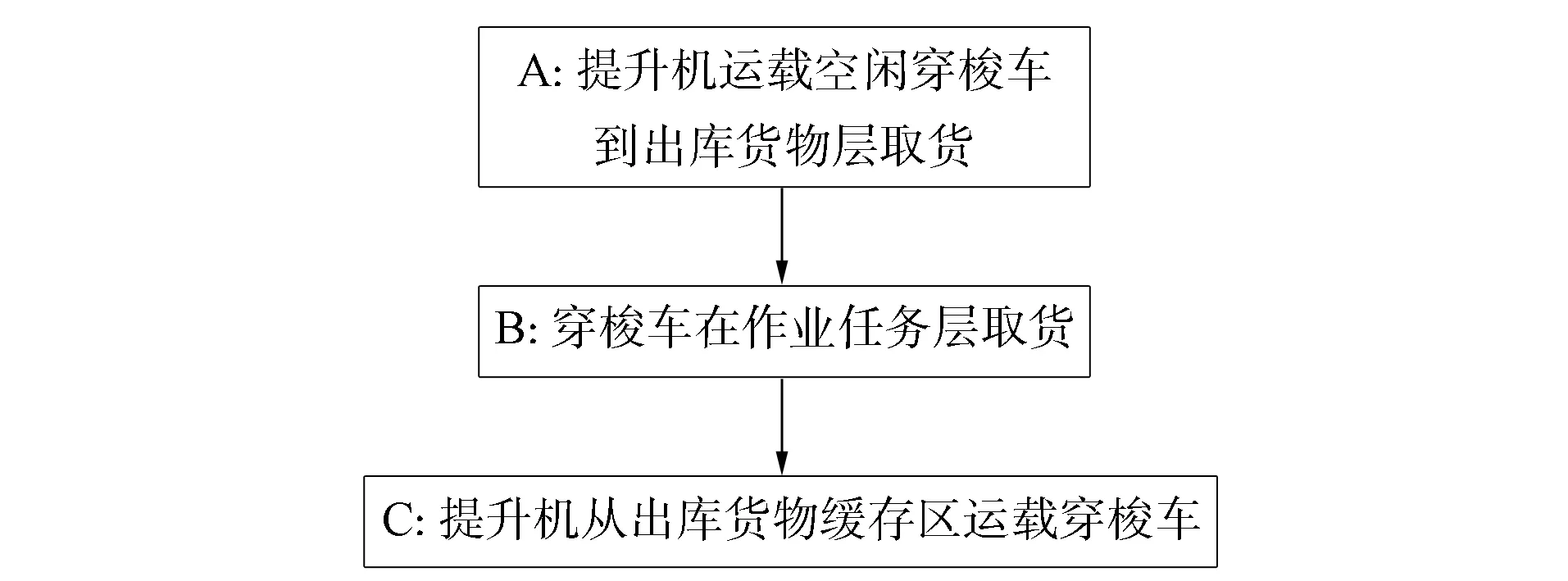
图2 出库作业任务时间段Fig.2 Outbound task time period

每台货物提升机的调用之间相互独立, 当一台货物提升机工作时不影响其他货物提升机的工作, 所有货物出库都需经过提升机与穿梭车配合实现, 且一台货物提升机服务多个巷道.因此, 以货物提升机为核心建立系统的工作时间模型.本文以货物提升机作业时间为中心建立系统作业任务的出库时间模型, 对出库作业任务所需时间进行研究.系统中出库作业任务可分为A,B,C三个时间阶段, 其简略流程如图2所示.

图3 穿梭车作业时序Fig.3 Shuttle operation sequence

A阶段： 如果出库任务在最底层则不需要提升机运载空闲穿梭车； 如果出库任务在其他层则需要提升机从当前所在层运行到第一层, 取空闲穿梭车将其运送到任务作业层, 然后穿梭车开始在作业任务层取货, 提升机等待或执行其他命令. B阶段： 穿梭车被提升机释放后沿货架之间的导轨开始运行到出库货位前取货, 取货完成后运送货物到提升机缓存区, 向提升机发出调用指令, 此时若提升机闲置则提升机响应该指令, 否则等待提升机响应. C阶段： 提升机响应穿梭车的调用申请, 从当前所在层运行至发送调用申请的载货穿梭车所在层, 将其运载至货架的最底层并将其卸载.

假设一个任务订单下达时, 系统随机分配3个任务给一台提升机执行, 分别由1,2,3号穿梭车运送, 穿梭车作业时序简图如图3所示. 由图3可见, 当系统给穿梭车发出指令时, 穿梭车开始申请调用提升机, 同时提升机在T0时刻开始按顺序运送空闲穿梭车到出库任务所在层, 在T1时刻提升机运送1号穿梭车到达出库作业任务所在层, 穿梭车开始取货, 提升机执行其他任务.在T1～T9时刻提升机按系统指令继续执行任务, 在T2时刻运送2号穿梭车到对应的出库任务层； 在T3时刻提升机运送3号穿梭车到任务层, 此时3号穿梭车开始取货, 提升机等待； 在T4时刻1号穿梭车运载出库货物请求调用提升机, 提升机响应调用请求, 开始从当前所在层运行至1号穿梭车所在层； 在T5时刻运送1号穿梭车至第一层并卸载穿梭车, 同时1号穿梭车对应的出库任务完成； 在T6时刻2号穿梭车运载出库货物请求调用提升机, 提升机响应并在T7时刻将其运送至第一层并卸载; 在T8时刻3号穿梭车完成取货任务运行到货物提升机缓存区请求调用提升机, 提升机响应3号穿梭车的请求; 在T9时刻将3号穿梭车运送至底层并释放完成出库任务.因此, 完成订单任务时提升机的工作时间为

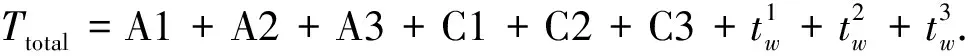
(3)

物理学中物体直线行驶的加速度与速度关系如图4所示, 其中vmax为物体行驶的最大速度,a为行物体行驶的加速度,t为物体行驶的时间.

图4 物体直线行驶时行驶速度与加速度的关系Fig.4 Relationship between speed and acceleration when object travels in straight line

在四向穿梭车系统中,vmax为提升机和穿梭车的最大运行速度,a为系统中提升机和穿梭车的加速度.从而可得系统中穿梭车和提升机的运行时间t与加速度a、 最大速度vmax及运行距离S的关系表达式为

(4)

由图3可知, 当进行第q个出库任务时, 该任务在A阶段所用的时间为

(5)

当yqi=1时, 表明第q个出库任务是提升机从第一层到第i层运送空闲穿梭车然后将其卸载.在该过程中, 提升机的工作时间由提升机的运行时间ti和卸载空闲穿梭车时间tL组成, 其中tL为固定时间.由式(5)可知,

(6)

其中Si为提升机从第一层到第i层运送空闲穿梭车行驶的距离,

Si=(i-1)h.

(7)

将式(7)代入式(6), 可得

(8)

当yqij=1时, 表明第q个出库任务是提升机从当前所在第i层向下运行至第一层取空闲穿梭车, 然后向上运行至第j层并卸载空闲穿梭车.在该过程中, 提升机的工作时间由提升机的向下运行时间ti、 向上运行时间tj和取空闲穿梭车及卸载空闲穿梭车时间2tL组成.同理可得：

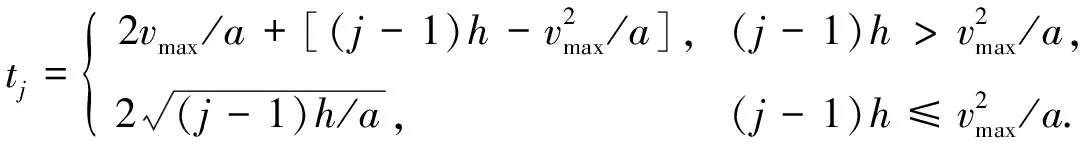
(9)

由图3可知, 当进行第q个出库任务时, 该任务在C阶段所用的时间为

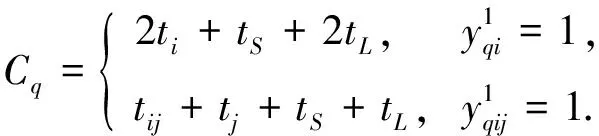
(10)

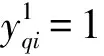
(11)

其中Sij为提升机从当前所在第i层运行到第j层行驶的距离,

Sij=|i-j|h.

(12)

将式(12)代入式(11), 可得

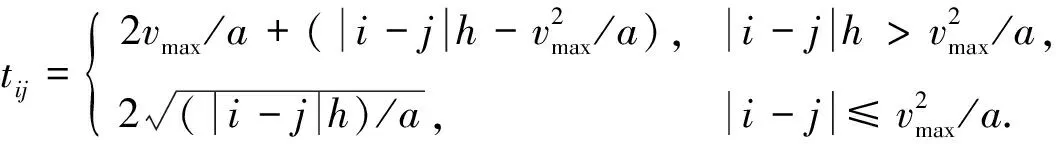
(13)

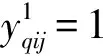
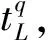
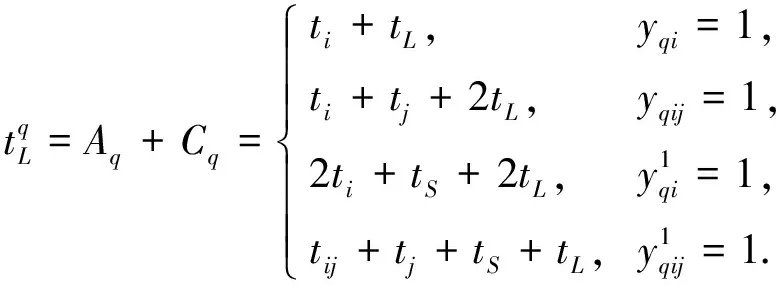
(14)

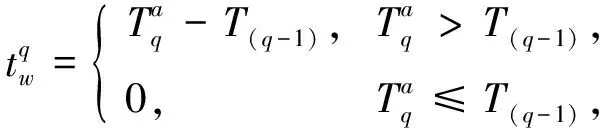
(15)

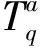
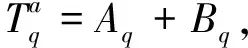
(16)

Bq=2×(tql+tqn)+tS,

(17)

式中Bq为四向穿梭车被货物提升机释放后运行到出库货物位置取货到运载货物到货物缓存区的时间,tql为四向穿梭车纵向运行时间,tqn为四向穿梭车横向运行时间,

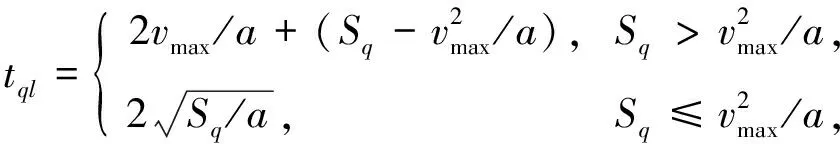
(18)

Sq=|Lq-Lf|·l,

(19)

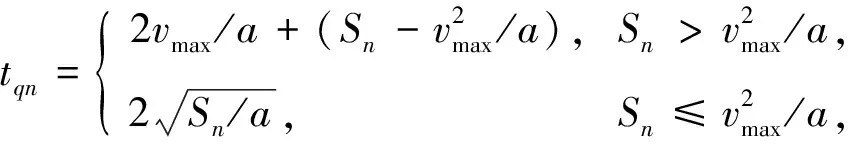
(20)

Sn=|Nn-Nf|·b,

(21)

l为货位的长度,b为货位的宽度.由式(3),(14),(15)可得出执行系统任务时一台提升机有Fq个出库任务时的工作时间为

(22)

综上可知, 当系统中有f台提升机时, 完成出库任务订单所需时间为

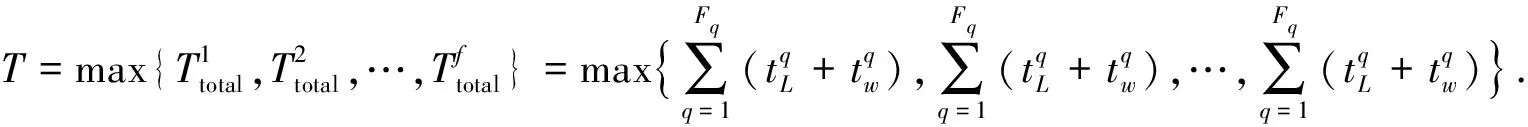
(23)

3 基于改进遗传算法的调度优化

3.1 遗传算法

当四向穿梭车系统进行出库作业时, 提升机和穿梭车的相互匹配问题实际上是寻找一个最佳的出库顺序并选择合适的提升机, 使完成出库作业任务的时间最短.遗传算法(GA)是根据自然界生物遗传规律提出的一种进化算法, 该算法在每次迭代中先选择群体中适应度较高的个体, 再通过交叉、 变异等进行反复迭代, 最后收敛到适应度最高的个体, 即可得到问题的最优解. 遗传算法具有良好的全局搜索能力, 能快速找到近似最优解.

3.1.1 编码与解码

在遗传算法中每个染色体都是所求问题的解, 因此染色体的编码对求解问题的最优解至关重要. 常见的染色体编码[14]主要有二进制编码、 实数编码等. 本文采用整数编码对任务序列及出库所对应的提升机序号进行求解, 设染色体个体表达方式为X=(x1,l1,x2,l2,…,xi,li), 其中xi为出库订单中的任务序列,li为执行任务时运载出库货物的提升机编号, 如X=(1,1,3,2,4,2,2,1,5,2,7,2,9,1,8,1,6,1,10,2), 奇数位的数字为一个出库订单中的出库任务号, 偶数位的数字为执行出库任务时对应的提升机编号, 系统按照(1,3,4,2,5,7,9,8,6,10)的任务序号执行出库任务, 出库货物分别由第1,2,2,1,2,2,1,1,1,2号提升机缓存区出库, 其中1号提升机按1,2,9,8,6的任务序列执行任务, 2号提升机按3,4,5,7,10的任务序列执行任务.

3.1.2 初始种群

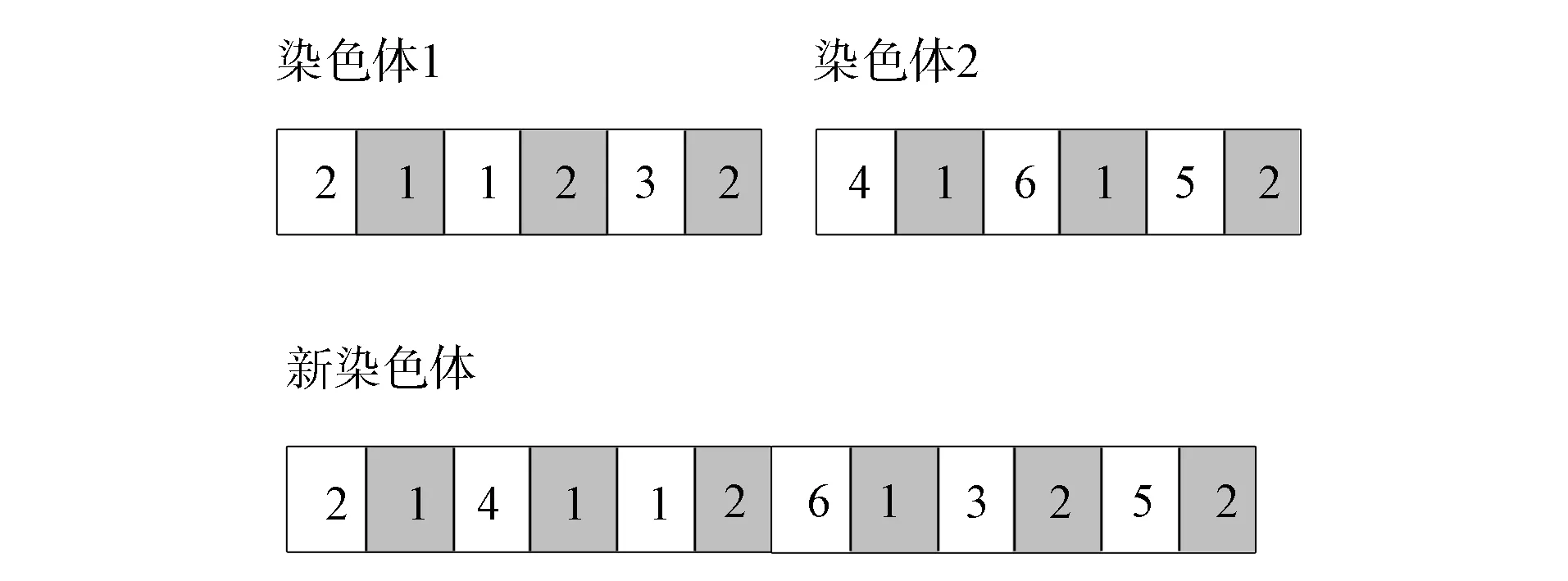
图5 染色体重组示意图Fig.5 Schematic diagram of chromosome recombination

根据染色体编码方式生成两个包含出库任务序列与货物提升机选择信息的染色体个体.将两个包含出库任务序列与货物提升机选择信息的染色体基因对相互错位连接重组, 构成一个新染色体个体, 如图5所示.由图5可见, 染色体1包含3个出库任务, 执行顺序为2,1,3, 分别选择第1,2,2号货物提升机执行任务.染色体2包含3个出库任务, 执行顺序为4,6,5, 分别选择第1,1,2号货物提升机执行任务.新染色体个体包含2个出库任务序列的出库顺序及货物提升机的选择信息, 包含6个出库任务, 执行顺序分别为2,4,1,6,3,5, 分别选择第1,1,2,1,2,2号货物提升机执行任务.根据新的染色体个体构成规则, 随机生成NP个新染色体, 即为一个初始种群.

3.1.3 适应度函数

本文针对系统出库任务需要的时间建模, 研究系统完成一个出库订单任务所需的作业时间, 因此执行出库任务所用最短时间适合做适应度函数.

fitness=min{T}.

(24)

3.1.4 选择

在遗传算法中染色体根据个体的适应度遗传给子代, 染色体个体适应度越高遗传给子代的概率越大.本文采用轮盘赌的方式选择适应度高的染色体个体作为父代遗传给子代, 从而使子代继承父代的优秀基因, 通过不断选择得到最高适应度的染色体个体.

3.1.5 交叉

交叉是指两个染色体通过交换部分基因片段重组为新染色体的过程.由于创建的染色体中部分片段含有出库顺序的基因和提升机选择信息, 因此本文采用随机调换基因组的方式对初始种群中的染色体进行重组, 构成一个新的染色体个体, 如图6所示.将包含两个订单的出库任务序列与货物提升机选择信息的基因片段作为一个基因组, 随机选取两个基因组互换位置.

3.1.6 变异

变异是指染色体个体的某个基因或部分基因发生突变, 变成新染色体的过程.本文将包含订单任务序列和货物提升机选择信息的基因片段作为一个基因对, 随机选取两个基因对采用随机调换位置的方式使这两个基因对调换位置, 对染色体上的基因进行变异, 如图7所示.

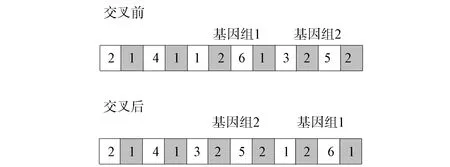
图6 染色体交叉示意图Fig.6 Schematic diagram of chromosome crossing

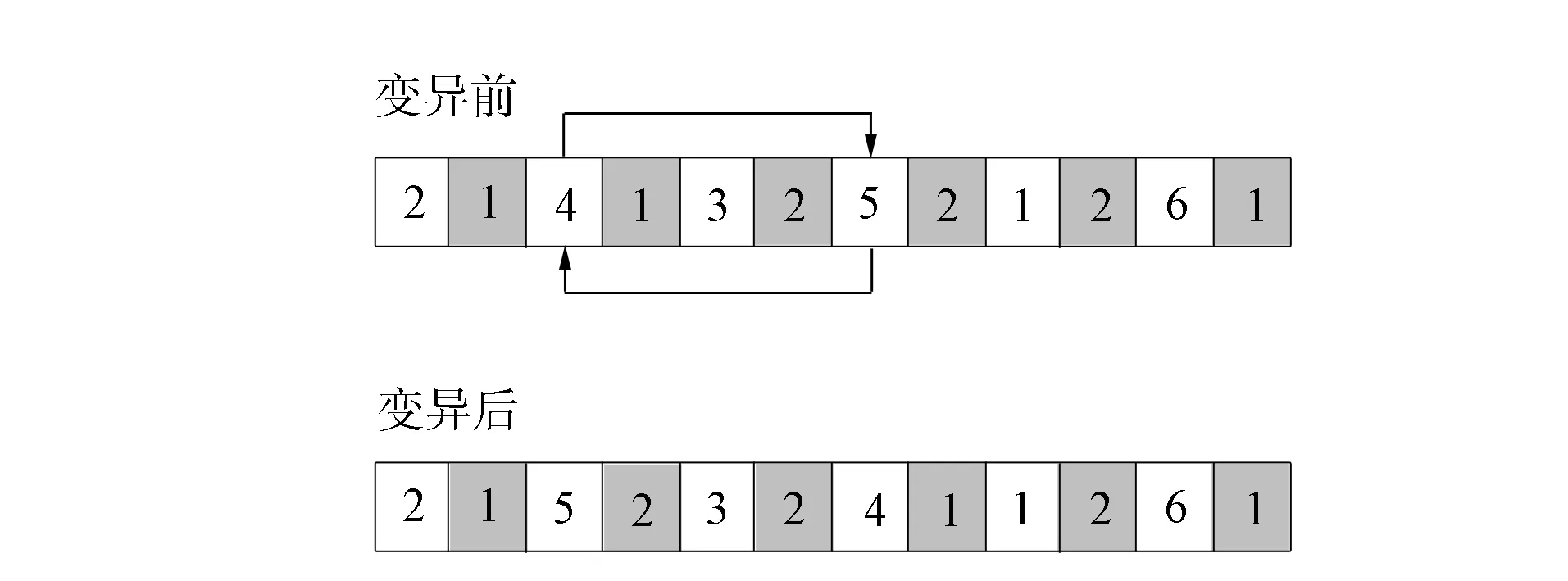
图7 染色体变异示意图Fig.7 Schematic diagram of chromosome variation

3.1.7 终止

本文通过设置最大迭代次数终止遗传算法的搜索, 当迭代次数达到设定值时, 输出最大适应度的染色体个体视为最优解.

3.2 自适应遗传退火算法

虽然遗传算法的全局搜索能力较强, 能在解空间中快速搜索出全体解, 但其局部搜索能力较差, 易产生早熟收敛的现象.模拟退火算法(SA)[15-16]是根据固体退火原理模拟组合优化问题, 采用随机搜索的方法从概率的角度上找出目标函数的最优解, 可在某种程度上避免搜索结果陷入局部最优值. 在遗传算法中交叉概率越大, 群体中新个体产生的速度越快, 算法的搜索能力越强, 当达到某种程度后种群中适应度较高的个体结构会遭到破坏, 种群中最优个体不会被保留； 变异概率达到某种程度后, 算法即变成了随机搜索算法[17]. 在标准遗传算法中交叉概率和变异概率都是固定值, 不会随种群中个体适应度的大小发生变化, 限制了算法的搜索能力. 本文对遗传算法中的交叉概率Pc和变异概率Pm进行自适应度调整设计, 并与模拟退火算法相结合, 提出一种自适应遗传退火算法(adaptive genetic simulated annealing algorithm, AGSAA), 以确保该算法拥有较强的搜索能力, 有效解决遗传算法局部搜索能力不足及产生早熟现象的问题, 提高算法的收敛性能. 其自适应度设计结果可表示为

(25)

其中:fmax为当前种群中目标函数的最大适应度值；favg为当前种群适应度值的平均值；f′为选中的交叉个体中的较大适应度值；f为变异个体的适应度值； 固定参数取值为c1=c2=0.9,m1=m2=0.5.其算法流程如图8所示, 算法步骤如下：

1) 初始化种群数量、 迭代次数、 温度及退温系数等；

2) 根据设置的编码方式生成初始种群；

3) 计算染色体个体的适应度, 选择染色体个体对其进行交叉与变异操作；

4) 判断是否迭代到设置的最大次数, 如果是则程序结束, 退出程序; 否则, 对染色体进行降温处理,T′=aT, 其中a为降温系数, 降温处理后返回步骤3)；

5) 输出所求的最优解, 结束程序.

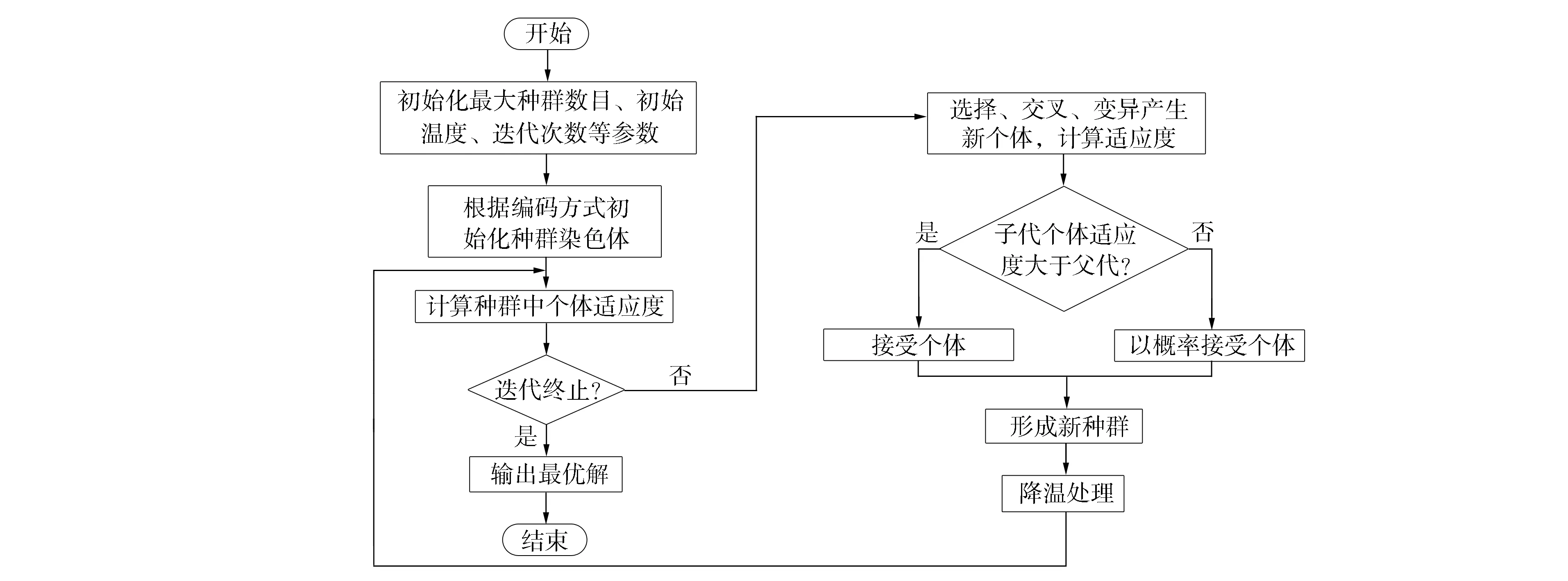
图8 自适应遗传退火算法流程Fig.8 Flow chart of adaptive genetic annealing algorithm

4 仿真实验与结果分析

4.1 初始化

以某灌装公司开发的四向穿梭车仓储系统为例, 该系统的参数列于表1.系统随机产生两个出库任务数量为10的订单任务列表, 如表2和表3所示.

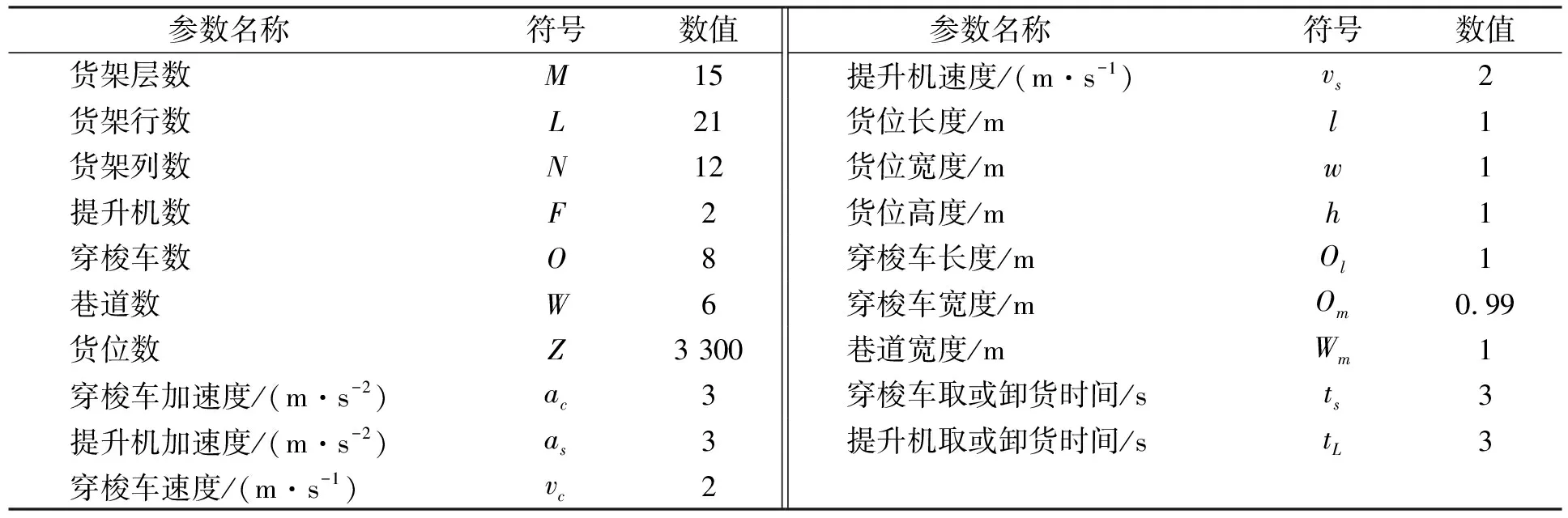
表1 系统参数

表2 订单1出库作业任务

表3 订单2出库作业任务

4.2 算例分析

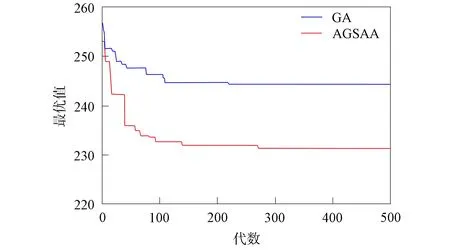
图9 出库时间最优值迭代曲线Fig.9 Iterative curves of optimal values of outbound time

为验证自适应遗传退火算法求解模型最优值的有效性, 对出库作业任务的时间进行求解验证. 遗传算法参数设置如下： 种群规模NP=40, 最大迭代次数maxgen=500, 交叉概率Pc=0.8, 变异概率Pm=0.2, 精英保留概率PGap=0.1. 自适应遗传退火算法的参数如下： 初始温度D0=1 000 ℃, 结束温度Df=900 ℃, 温度下降比例a=0.99, 种群规模NP=40, 最大迭代次数maxgen=500, 精英保留概率PGap=0.1. 两种算法运行的出库时间最优值迭代过程如图9所示, 对应的1号货物提升机出库时间迭代过程如图10所示, 对应的2号货物提升机出库时间迭代过程如图11所示.

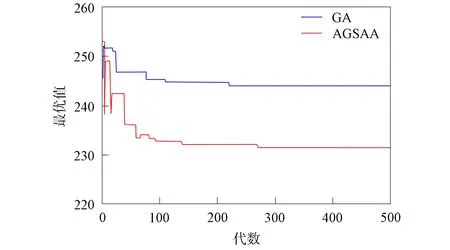
图10 1号提升机作业时间迭代曲线Fig.10 Iterative curves of operation time of number one elevator

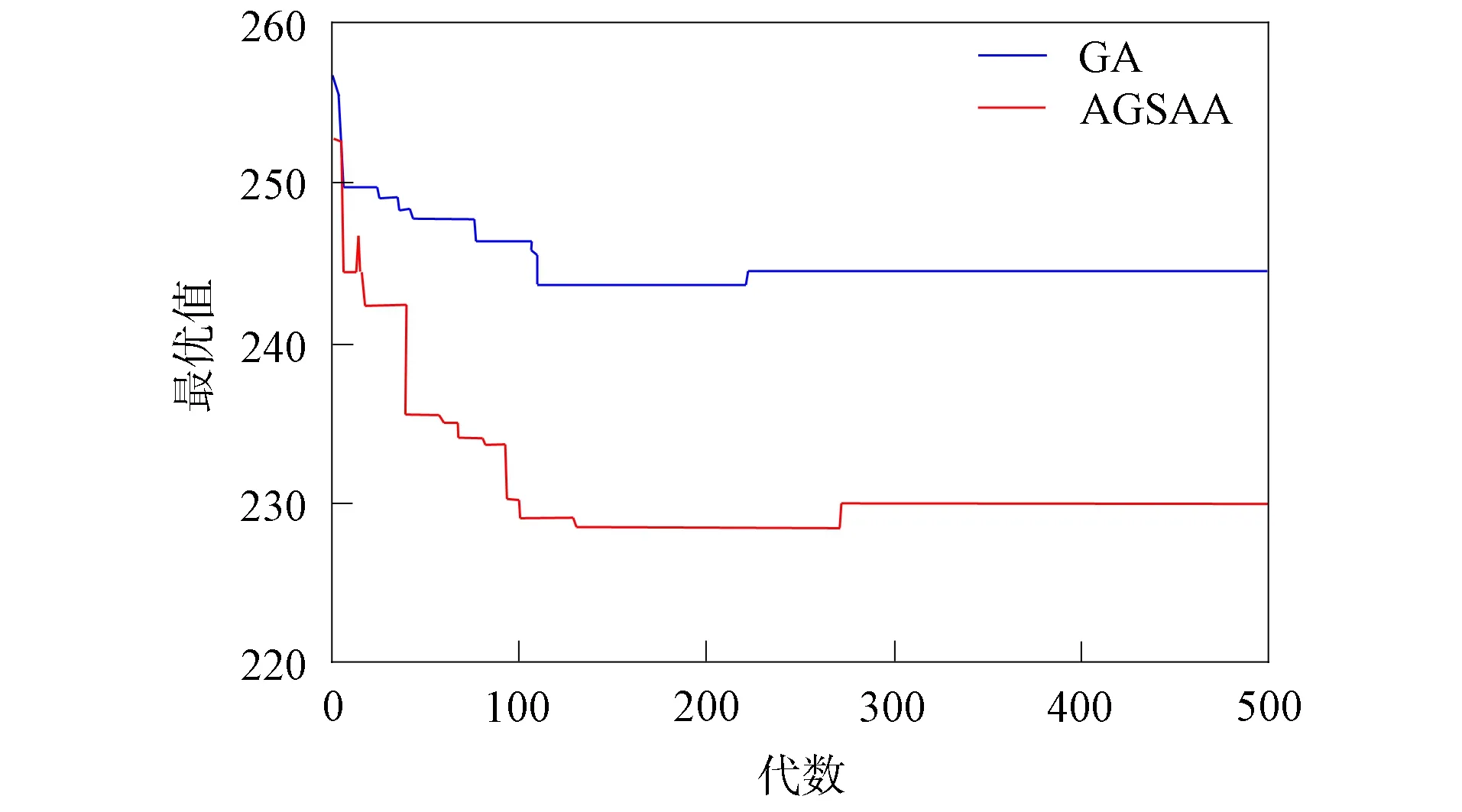
图11 2号提升机作业时间迭代曲线Fig.11 Iterative curves of operation time of number two elevator

由图9～图11可见, 图9中的系统出库时间为1号提升机和2号提升机工作时间中的最大值, 随着迭代次数的增加, 1号提升机和2号提升机的工作时间趋于稳定, 同时系统的作业时间也趋于稳定. 由图9可见: GA算法在寻找最优解的过程中易陷入局部最优解, 不易从局部最优解中跳出, 且后期收敛过程缓慢； AGSAA算法能从局部最优解中跳出, 比GA算法的求解结果更好. 表4为两种算法分别运行10次最优值的结果.

表4 两种算法运行结果

图12 四向穿梭车执行出库作业任务时的出库路径Fig.12 Outbound path of four-way shuttle when performing outbound tasks

由表4可见, GA的最优解为244.333 3 s, AGSAA的最优解为231.333 3 s； GA解的平均值为244.773 3 s, GA解的标准偏差为0.440 2%； AGSAA解的平均值为231.666 7 s, AGSAA解的标准偏差为0.415 7%. 因此, AGSAA的求解结果比GA的求解结果优化了4.533 4 s, 且AGSAA最优解的标准偏差比GA的小, 证明了AGSAA求解最优值的有效性, 比GA求解的结果更稳定. 经过AGSAA运算可以得到一条最优解的染色体X=(2,1,11,1,5,1,13,2,8,1,17,1,6,2,12,1,9,2,20,2,7,2,18,2,10,2,16,2,1,1,19,1,3,2,14,1,4,2,15,1).对该染色体进行解码, 可知系统按2,11,5,13,8,17,6,12,9,1,20,7,18,10,16,1,19,3,14,4,15的任务序列执行订单1与订单2的出库作业任务, 订单1的出库任务按2,5,8,6,9,7,10,1,3,4的出库顺序执行, 分别使用第1,1,1,2,2,2,2,1,2,2号货物提升机执行出库任务； 订单2的出库任务按11,13,17,12,20,18,16,19,14,15的出库顺序执行, 分别使用第1,2,1,1,2,2,2,1,1,1号货物提升机执行出库任务, 完成出库任务所需时间为231.333 3 s. 自适应遗传退火算法求解的最优解可在三维坐标系中表示, 将穿梭车视为一个质点, 如图12所示, 其中蓝色轨迹为四向穿梭车通过1号货物提升机调度执行出库作业任务时的路径, 红色轨迹为四向穿梭车通过2号货物提升机调度执行出库作业任务时的路径. 四向穿梭车执行出库作业任务时的路径如下：

F1(0.5,4.5,0),(0.5,4.5,4),(0.5,9.5,4)； (0.5,4.5,0),(0.5,4.5,4),(0.5,10.5,4),(12.5,10.5,4)； (0.5,4.5,0),(0.5,4.5,7),(0.5,1.5,7),(5.5,1.5,7)； (0.5,4.5,0),(0.5,4.5,7),(16.5,1.5,7)； (0.5,4.5,0),(0.5,4.5,7),(0.5,10.5,7),(5.5,10.5,7)； (0.5,4.5,0),(0.5,4.5,9),(0.5,1.5,9),(2.5,4.5,9)； (0.5,4.5,0),(0.5,4.5,9),(0.5,7.5,9),(10.5,7.5,9)； (0.5,4.5,0),(0.5,4.5,14), (0.5,1.5,14),(7.5,1.5,14)； (0.5,4.5,14),(0.5,4.5,14),(12.5,4.5,14)； (0.5,4.5,14),(0.5,4.5,14),(0.5,10.5,14),(14.5,10.5,14)；

F2(0.5,13.5,0),(0.5,13.5,4),(0.5,7.5,4),(3.5,7.5,4)； (0.5,13.5,0),(0.5,13.5,4),(7.5,13.5,4)； (0.5,13.5,0),(0.5,13.5,7),(0.5,7.5,7),(18.5,7.5,7)； (0.5,13.5,0),(0.5,13.5,7),(0.5,16.5,7),(8.5,16.5,7)； (0.5,13.5,0),(0.5,13.5,9),(0.5,4.5,9),(8.5,4.5,9)； (0.5,13.5,0),(0.5,13.5,9),(0.5,10.5,9),(1.5,10.5,9)； (0.5,13.5,0),(0.5,13.5,9),(15.5,13.5,9)； (0.5,13.5,0),(0.5,13.5,9),(0.5,16.5,9),(17.5,16.5,9)； (0.5,13.5,0),(0.5,13.5,14),(0.5,7.5,14),(19.5,10.5,14)； (0.5,13.5,0),(0.5,13.5,14),(19.5,13.5,14).

综上所述, 本文针对四向穿梭车仓储系统无法同时处理多订单作业任务的问题, 以货物提升机为时间轴建立了系统出库作业任务的时间模型, 并设计了一种包含多个订单作业任务顺序和货物提升机选择信息的染色体, 采用遗传算法对模型求解. 为解决遗传算法易陷入局部最优解的问题, 提出了一种自适应遗传退火算法, 对遗传退火算法中的变异概率和交叉概率进行自适应调整, 同时融合模拟退火算法增加算法的搜索范围. 通过实验证明了自适应遗传退火算法与遗传算法相比搜索能力更强； 通过运用自适应遗传退火算法得到一个最优的染色体并对其解码, 得到多个订单任务的出库顺序及选择的货物提升机信息, 实现了对出库货物的最优路径规划.