二叉树队列关系问题非递归算法的推导及形式化证明
左正康,方 越,黄志鹏,黄 箐,王昌晶
(江西师范大学计算机信息工程学院,江西 南昌 330022)
0 引言
二叉树是在计算机科学中一种经典的非线性数据结构,它不仅能够提供有规律的数据存储还能支持强大的搜索算法.二叉树递归算法简单、易理解,但它需要更多的运行时间和存储空间;而非递归算法的效率要远高于递归算法,因此二叉树非递归算法的推导及形式化证明具有重要的价值.通过分析被求解二叉树问题的背景知识和相关数学特性,对二叉树类问题进行分划,确定二叉树可以用2种方式来求解序列的递推关系:栈和队列.本文给出了二叉树队列关系问题推导和形式化证明策略,结合具有队列递推关系(简称“队列关系”)的这一类问题来验证策略的正确性和实用性.由于二叉树非递归算法的代码复杂、难以理解,而且证明过程晦涩难懂,正确性得不到保证[1],因此如何推导及形式化证明二叉树队列关系问题非递归算法成为一大难点.
开发二叉树非递归算法的循环不变式一直是形式化开发的难点[2],循环不变式是理解、推导和证明循环程序的基础[3-4].文献[5-6]提供了前序遍历二叉树非递归算法的循环不变式,但是表达十分烦琐,逻辑关系较为复杂,没有很好的可行性和实用性.本文通过开发众多二叉树队列关系问题非递归算法的循环不变式,发现循环不变式之间的共性和特性.由此,提出了开发二叉树队列关系问题循环不变式的3种策略和二叉树队列关系问题通用循环不变式的模板.
本文通过推导3类派生问题为代表,分别是基于层次遍历二叉树派生出的问题、基于求二叉树深度派生出的问题以及基于层次遍历二叉树和求二叉树深度共同派生出的问题,得到递推关系表达式和循环不变式,由此导出抽象程序设计语言Apla(Abstract Programming Language)[2,4,7]程序,极大地提高了算法的开发效率;然后,用Dijkstra-Gries标准程序证明方法证明了这些算法的正确性;最后通过“Apla到C++程序自动生成系统”自动生成可执行程序[8].
1 相关工作
开发正确的算法程序是计算机科学的核心.通常人们是针对已编好的程序来测试验证该程序是否正确,尽可能地找出程序的漏洞,但是该方法无法从根本上保证算法程序的正确性.于是,出现了越来越多的形式化推导方法,将待解决问题精确地描述出来,再根据各方法的形式化规则进行推理,最终得出正确的结构化程序[9].目前,存在着大量的形式化推导方法,其中E. W. Djkstra[6]提出的最弱前置谓词方法wp(Q,R)是程序求解变换的经典方法之一.给出程序规约,并将验证程序正确性的理论融入开发过程中,在开发过程中保证了程序的正确性.该方法自动化程度低,对于复杂的算法难以进行推导.D.L. Chaudhari等[10]提出的推导方法是在最弱谓词方法的基础上,将后置断言不断拆分,直至开发出循环不变式,但该方法在处理复杂问题上还是存在着较大的困难.D.G. Kourie等[11]提出了一种结合Dijkstra的GCL和Morgan的细化演算规则的方法,依靠经验推测循环不变式,这导致在推导过程中非常依赖循环不变式,存在很大的不确定性.D.L. Chaudhari等[12]无缝地将自下而上的技术结合到自上而下的推导方法中,以此避免不必要的回溯和相关的返工,提出了新的推导策略,以捕捉在自上而下阶段中所做的假设,并随后将这些假设反向传播到适当的程序位置,并在 CAPS 系统中实现了这种方法.
开发正确迭代程序的关键是循环不变式,这已经被程序设计和形式化方法方面的专家所认可,循环不变式是程序设计理论中的一个重要概念,在形式化证明中承担着至关重要的作用[13].循环不变式不仅可以用来分析程序的性质,而且可以用来证明循环程序的正确性,但是开发循环不变式的标准策略仅仅适用于一些简单的算法程序,对于复杂的算法程序仍无较好的办法.T. Hoare认为循环不变式不能通过简单的规则计算来验证.为了获得适当的循环不变式,通常需要人工干预才能完成.目前只能针对特定的情况提出了一些启发式的方法,没有一种通用的方法可以对所有的情况得到正确的结果[14].一般来说,对于一个给定函数的前置断言和后置断言,循环不变式并不是唯一的,开发者往往会逐步得到循环不变式:首先猜测出粗略的循环不变式,然后通过观察程序的行为逐步精化循环不变式,最后证明需要的信息是否正确[15].开发循环不变式一般的方法是假定程序中的变量在无限范围上求值.然而,变量在程序执行过程中由有限长度的位向量表示.在无限范围上的循环不变量式可能不再是在有限范围程序中的循环不变量式,反之也是如此[16].采用消元法对程序进行验证[17],可生成非线性循环不变式,并判定循环程序的终止性,如基于Dixon结式.M.D. Ernst等[18]提出了循环不变式的动态探测技术,并设计了动态监测器来实现此技术.
二叉树是计算机科学中一种经典的非线性数据结构,有强大的功能和效率,因此二叉树的推导和形式化证明具有非常重要的意义.D. Gries[5]对E.W. Dijkstra[6]提出的构造循环不变式开发策略进行了补充和解释,提供了前序遍历二叉树非递归算法的循环不变式.在二叉树非递归算法的形式化验证上,秦胜潮等[19]用HIP/SLEEK形式化验证了AVL树和二叉搜索树.
目前,二叉树的推导是基于最弱前置谓词方法,其推导过程烦琐,循环不变式较为复杂.本文提出的推导方法是基于严格的数理逻辑,对原算法程序规约进行了一系列的求精变换步骤.每一步都减少了一定的抽象程度或增加了一定的程序可执行性,大大降低了在算法求精过程中的创造性工作.并且,开发循环不变式的策略是一种基于递归定义技术来开发具有固有递归性质的迭代程序的循环不变式,提高了开发效率.
2 二叉树队列关系问题推导及形式化证明策略
2.1 求解步骤
对二叉树类问题进行分划,寻找递推关系.关于求解序列的递推关系为队列的这类问题,通过推导及形式化证明,总结出如下7个步骤:
(i)构造算法程序规约.构造形式化规约来明确二叉树队列关系问题的任务目标,程序规约是由程序的前置断言(AQ)和后置断言(AR)构成.对于二叉树队列关系问题的非递归算法,前置断言均为给定1个有限的二叉树T;后置断言根据求解问题的定义和实现的功能以形式化语言描述程序达到所要的目的.虽然后置断言只有1个,但是为了供后续更容易地推导算法,可以分划出求解问题的关键功能,对这部分功能构造出新的形式化规约.
(ii)分划原问题.二叉树队列关系问题的算法或递推关系均由分划决定,不同的算法会有不同的分划,可以从步骤(i)中形式规约得到分划二叉树队列关系问题的启示:划分二叉树,得到一定数量的子树,子树需满足结构与原二叉树相同但规模比原二叉树更小的特征,再把子树进行相同方式划分,直到求解出每一个子树.
(iii)寻找递推关系.通过分析二叉树问题的背景知识和数学特性,确定其求解序列的递推关系和所需的全部循环变量,用谓词精确表达它们的变化规律.二叉树拥有2种求解序列的递推关系:栈和队列.
对于队列,可以看成是一个序列q[0…#q-1],并规定q[0]端为队头,q[#q-1]为队尾,则队列的常用操作可以用如下序列的操作加以实现:
(a)测试队列是否为空,即#q=0;
(b)引用队列头元素,即X:=q[0];
(c)对队列q实施进队,即q:=q↑[X];
(d)对队列q实施出队,即q:=q[1…].
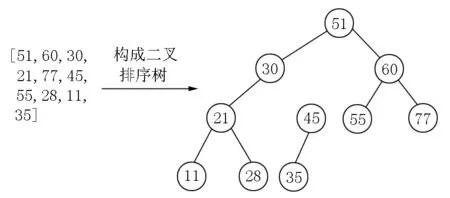
将队列及其运算封装在一起构成抽象数据类型,用量词转换法推导出队列问题求解序列的递推关系Si=F(Sj),Si是其子解Sj的函数,其中1 (iv)构造循环不变式.通过步骤(iii)构造的递推关系表达式,采用本文提出的开发二叉树队列关系问题循环不变式的策略,使用循环不变式递归定义技术,并结合二叉树队列关系问题通用循环不变式模板,根据不同问题的特性和要求,以此开发该问题的循环不变式. (v)导出非递归算法Apla程序.依据步骤(iii)统一的递推关系和步骤(iv)统一的循环不变式,推导出二叉树队列关系问题的Apla算法程序. (vi)形式化证明.通过Dijkstra-Gries标准程序证明法证明Apla算法程序的正确性. (vii)生成C++程序.通过“Apla到C++程序自动生成系统”自动生成C++可执行程序. E.W. Dijkstra和D. Gries给出了4个循环不变式的传统开发策略[20],D. Gries对其进行了解释和补充,开发了前序遍历二叉树非递归算法的循环不变式[5-6]: ρ:0≤c≤#p∧fpreorder(p)=b[0:c-1]|fpreorder(r0)|fpreporder(r1)…|fpreorder(rr-1). 观察该循环不变式,看出此循环不变式用“…”表示显得冗长、不易理解.于是,使用循环不变式的递归定义技术,重新对前序遍历二叉树非递归算法的循环不变式进行开发[4]: ρ:HPre(T)=X↑HPre(q)↑F(S), 该循环不变式引进了3个辅助变量:X,S,q.其中X存放已遍历的结点序列;S是起堆栈作用的变量,用于存放尚待遍历的T的右子树;q用于存放正准备遍历的T的子树. 比较以上2个循环不变式,可以很清晰地发现本文的循环不变式更简单、精确.因此,以文献[21-22]提出的开发循环不变式的新定义和新的开发策略为基础,提出了对二叉树队列关系问题开发循环不变式的策略. 先写出其前置断言和后置断言,前置断言均为“给定一个有限的二叉树T”,而后置断言的不同则决定着每个问题是属于什么输出类型,再根据问题的实现思路,并结合后置断言,可将开发二叉树队列关系问题循环不变式的策略分为3种. 策略1输出结果为结点序列的问题. 通过分析求解问题的特性,确定后置断言为X=算法F(T)形式,以表明输出结果为结点序列.通过分划递推,寻找序列变量和队列存放待求解子问题的变化规律,以此推导出递推关系,并确定循环变量,采用递归定义技术定义序列变量和队列中的内容,即构成所需的循环不变式. 策略2输出结果为固定值的问题. 根据求解问题的定义和实现的功能,确定后置断言为算法F(T)=固定值,以表明输出结果为固定值.通过分划递推,寻找能判别待求解子问题的固定值变化规律是否均满足求解问题需实现功能的约束条件的这一规律,以此推导出递推关系,并结合队列存放待求解子问题的变化规律,确定循环变量,采用递归定义技术定义固定值、序列变量和队列中元素的组成,即构成所需的循环不变式. 策略3输出结果为属性判断的问题. 根据求解问题的定义和实现的功能,确定后置断言为算法F(T)=对于任一结点的该问题的属性判断均为真,以表明输出结果为true或false.通过分划递推,寻找待求解子问题的属性判断变化规律是否均满足求解问题需实现功能的约束条件的这一规律,以此推导出递推关系,并结合队列存放待求解子问题的变化规律,确定循环变量,再采用递归定义技术定义属性判断、序列变量和队列中元素的组成,即构成所需的循环不变式. 在推导出众多二叉树队列关系问题得出的循环不变式过程中,发现每个问题的循环不变式都存在共性.因此,构造一个二叉树队列关系问题通用循环不变式模板,供后续开发更多的二叉树队列关系问题.该模板形式为 ρ:HLay(T)=X↑[q.d]↑F(S↑[q.l]↑[q.r])∧P(x), 其中HLay(T)=X↑[q.d]↑F(S↑[q.l]↑[q.r])为层次遍历二叉树的循环不变式.序列变量X用于存放已访问的结点标志序列,当有限二叉树遍历结束时,X=HLay(T);S为队列,用来存放待访问的顶点;h为序列头的域名;q用于存放正在访问的顶点.在队列S中的首元素为即将访问的顶点,且在被访问后,该顶点的未被遍历的相邻顶点要作为待访问顶点进入队列.所以S中的内容由函数F定义为 F([])=[], (1) F(S)=[S.h]↑F(S[h+1..t]↑[S[h].l]↑ [S[h].r]); (2) 当q未访问时, F([q↑S])=[q.d]↑F(S↑[q.l]↑[q.r]), (3) 当q已访问时, F([q↑S])=F(S). (4) P(x)是指根据不同问题的特性和要求,合取满足条件的断言. 抽象程序设计语言Apla[4]提供了序列(list)和二叉树(btree)预定义的ADT类型,下面给出本文中所用的序列和二叉树ADT相关数据和操作说明. 2.4.1 序列 关于序列的定义和操作如下: varh,t:integer:=0,0;//t表示序列尾的域名; varS,T:list:=[],[];//S和T为序列; X:data;i,j:integer;//X是序列中的元素; []//序列为空; [X]//序列中有一个元素X; #(S)//计算S中元素的个数; S[i]//S的第i个元素,S.h≤i≤S.t; S[i..j]//S的子序列,S.h≤i,j≤S.t; S↑T//S的尾和T的头用“↑”运算合成一个新序列. 2.4.2 二叉树 关于二叉树的定义和操作如下: T.d//产生二叉树T的根结点; T.l//产生二叉树T的左子树; T.r//产生二叉树T的右子树; n+T//把结点n加到T中,使T成为和T结构相同的新树; ReadNode(n)//建立结点n; WriteNode(n)//输出结点n. 通过深入研究大量二叉树队列关系问题非递归算法,思考各个问题的思想和数据结构特性,寻找它们的共性和特性,发现很多算法可以在实现母算法功能的同时增添符合该问题的功能实现条件,以此最终实现该问题.因此,将层次遍历二叉树和求二叉树深度作为母算法,将二叉树队列关系问题分为3类派生问题(见图1). (i)基于层次遍历二叉树派生出的问题:以判断完满二叉树为例.在层次遍历二叉树的同时判断当前结点有几个孩子,若有2个或0个则继续判断队列中的下一个结点;若有1个则不是完满二叉树.直至层次遍历完所有结点,若所有节点均满足条件,则该二叉树为完满二叉树. (ii)基于求二叉树深度派生出的问题:以判断一颗具有xsize个结点二叉树是否为满二叉树为例.在求出二叉树深度为xheight后,若满足2xheight-1=xsize,则是满二叉树,否则不是满二叉树. (iii)基于层次遍历二叉树和求二叉树深度共同派生出的问题:以判断平衡二叉树为例.在层次遍历二叉树的同时以当前结点作为根结点,通过求二叉树深度的功能判断左右子树的深度之差的绝对值是否小于等于1,若满足则继续判断队列中的下一个结点,若不满足则不是平衡二叉树.直至层次遍历完所有结点,若所有节点均满足条件,则该二叉树为平衡二叉树. 图1 3类派生问题 层次遍历二叉树和求二叉树深度对二叉树队列关系问题非递归算法的推导起着至关重要的作用.若2个母算法成功推导,则这便于派生问题的推导,也有助于更好地发现3类派生问题循环不变式的共性和特性.因此,需要先对这2个母算法进行推导. 3.1.1 层次遍历二叉树 文献[23]已经成功推导出层次遍历二叉树非递归算法的循环不变式: ρ:HLay(T)=X↑[q.d]↑F(S↑[q.l]↑[q.r]) 以及非递归算法Apla程序: do ┐(q=%)→S,X,q:=S↑[q.l]↑[q.r],X↑[q.d],%; [] ┐(S=[])→q,S:=S[h],S[h+1..t]; od. 3.1.2 求二叉树深度 文献[23]已经成功推导出求二叉树深度非递归算法的循环不变式: ρ:h=[(N,n:0≤n:n=#(S))-1]∧HLay(T)=X↑[q.d]↑F(S↑[q.l]↑[q.r]) 以及非递归算法Apla程序: do (num≥1)→q,S:=S[S.h],S[S.h+1..S.t]; X:=X↑[q.d]; if (q.l≠%)→S:=S↑[q.l];fi; if (q.r≠%)→S:=S↑[q.r];fi; n:=n-1; [] ┐(q=%)→n,h,q:=#(S),h+1,%; od. 限于篇幅,本节以判断平衡二叉树为实例,完整地展现如何基于母算法推导派生问题. (i)算法程序规约.用HLay(T)表示T的层次遍历产生的结点序列,存放已访问的结点标志序列在序列变量X中,X=HLay(T).LDepth(T)表示T的深度.abs() 函数表示返回数字的绝对值.用abs(LDepth(q.l)-LDepth(q.r))≤1来判断当前结点q左右子树的深度之差的绝对值是否符合判断条件,若满足abs(LDepth(q.l)-LDepth(q.r))≤1,则继续层次遍历下一个结点,重复此操作,直至遍历结束.若fBalance(T)=true,则T是平衡二叉树;若fBalance(T)=false,则T不是平衡二叉树.即求解问题的算法规约: |[X:list (integer,40);T:btree (integer,40);msize:integer]|; AQ:给定一个有限的二叉树T; AR:fBalance(T)=∀(a:a∈HLay(T):abs(LDepth(a.l)-LDepth(a.r))≤1). 创建布尔变量isbalance(a)函数记录abs(LDepth(a.l)-LDepth(a.r))≤1的判断结果. (ii)寻找递推关系.根据判断完全二叉树的算法程序规约,仅需寻找fPerfect(T)的递推关系: 若T=%,则fBalance(T)=true; 若T≠%,则为了得到一个非递归的算法程序,分划fBalance(T),得到递推关系为 fBalance(T)=(isbalance(T)=true)∧fBalance(T.l)∧fBalance(T.r)=(isbalance(T)=true)∧(isbalance(T.l)=true)∧fBalance(T.l.l)∧fBalance(T.l.r)∧fBalance(T.r)=…. 由以上递推关系发现:该过程是通过层次遍历二叉树HLay(T)来表示二叉树T中所有结点构成的一个序列X.在实现过程中,必须使用队列S存放待访问的顶点,q用于存放正在访问的顶点,序列变量X用来存放已访问的结点标志序列,当有限二叉树遍历结束时,X=HLay(T). (iii)构造循环不变式.由于X存放了层次遍历后的结点序列,因此flag的值始终依赖于X中的结点,即有如下性质成立: flag=∀(a:a∈X:isbalance(a)=true). 因此,上式与HLay(T)的循环不变式合取即构成本问题算法程序的循环不变式: ρ:HLay(T)=X↑[q.d]↑F(S↑[q.l]↑[q.r])∧flag=∀(a:a∈X:isbalance(a)=true). (iv)非递归算法Apla程序.通过递推关系(ii)和循环不变式(iii),简捷地导出Apla语言过程: procedurefBalance(T:btree(integer,40);varX:list(integer,40)); begin X,S,q,flag:=[],[],T,true; {ρ:HLay(T)=X↑[q.d]↑F(S↑[q.l]↑[q.r])∧flag=∀(a:a∈X:isbalance(a)=true)}; doflag∧(┐(q=%)∨┐(S=[]))→if (q≠%)∧(isbalance(q)=true)→flag,X,S,q:=true,X↑[q.d],S↑[q.l]↑[q.r],%; [] (q≠%)∧(isbalance(q)=false)→flag,X,S,q:=false,X↑[q.d],S↑[q.l]↑[q.r],%; [] (q=%)∧┐(S=[])→q,S:=S[S.h],S[S.h+1..S.t];fi; od; if(flag=true)→ writeln(“是平衡二叉树”); []→writeln(“不是平衡二叉树”); fi; end. Dijkstra-Gries标准程序证明法是形式化证明的重要方法,通过证明{Q}S{R}的正确性,以此来验证算法程序的正确性.S表示语句,Q表示谓词公式或S的前置断言,R表示谓词公式或S的后置断言.对于二叉树队列关系问题,由于此类问题是循环语句do的一般形式,所以基于在Dijkstra-Gries标准程序证明法中循环语句do的证明条件来证明二叉树队列关系问题.本节以判断平衡二叉树为例,详细地展现如何形式化证明二叉树队列关系问题. (i)证明在执行循环之前ρ是正确的. 由于断言中给出的AQ并非do语句中的AQ,而是整个程序的AQ.因此,若为保证do语句执行开始迭代之前ρ为真,使得AQ⟹ρ,则必须保证如下断言成立: 语句S0为S,X,q,flag:=[],[],T,true, AQ⟹wp(S0,ρ)≡(HLay(T)=X↑[q.d]↑F(S↑ HLay(T)=[]↑[T.d]↑F([T.l]↑[T.r])∧true=∀(a:a∈X:isbalance(a)=true); {使用递推关系式(4)}≡true. 将声明S0中的3个变量赋值给ρ,显然实现AQ⟹wp(S0,ρ),显然上述断言成立. (ii)证明ρ是循环不变式. 用布尔变量flag记录fBalance(T)的判断结果,可更深地进行细化,便于下面形式化证明: ∀(a:a∈HLay(T):isbalance(a)=true)→flag=true∨∃(a:a∈HLay(T):isbalance(a)=false)→flag=false. (a)针对循环体中的第1个条件子句: 条件C1为flag∧(┐(q=%)∨┐(S=[]))∧(q≠%)∧(isbalance(q)=true) 语句S1为flag,X,S,q:=true,X↑[q.d],S↑[q.l]↑[q.r],%; [q.l]↑[q.r])∧flag=∀(a:a∈X:isbalance(a)=true)∧flag∧(┐(q=%)∨┐(S=[]))∧(q≠%)∧(isbalance(q)=true)⟹HLay(T)=X↑F(S)∧true=∀(a:a∈X↑[%]:isbalance(a)=true); {使用递推关系式(4)}≡true. 将声明S1中的3个变量赋值给ρ,实现ρ∧C1⟹wp(S1,ρ),显然第1个条件子句成立. (b)针对循环体中的第2个条件子句: 条件C2为flag∧(┐(q=%)∨┐(S=[]))∧(q≠%)∧(isbalance(q)=false); 语句S2为flag,X,S,q:=false,X↑[q.d],S↑[q.l]↑[q.r],%; {使用递推关系式(3)和递推关系式(4)}≡HLay(T)=X↑[q.d]↑F(S↑[q.l]↑[q.r])∧flag=∀(a:a∈X:isbalance(a)=true)∧flag∧(┐(q=%)∨┐(S=[]))∧(q≠%)∧(isbalance(q)=false)⟹HLay(T)=X↑F(S)∧false=∀(a:a∈X↑[%]:isbalance(a)=true)≡true. 将声明S2中的2个变量赋值给ρ,实现ρ∧C2⟹wp(S2,ρ),显然第2个条件子句成立. (c)针对循环体中的第3条件子句: 条件C3为flag∧(┐(q=%)∨┐(S=[]))∧(q=%)∧┐(S=[]); 语句S3为q,S:=S[S.h],S[S.h+1..S.t]; {使用递推关系式(3)和递推关系式(4)}≡HLay(T)=X↑[q.d]↑F(S↑[q.l]↑[q.r])∧flag=∀(a:a∈X:isbalance(a)=true)∧flag∧(┐(q=%)∨┐(S=[]))∧(q=%)∧┐(S=[])⟹(HLay(T)=X↑F(S)∧flag=∀(a:a∈X:isbalance(a)=true)≡true. 将声明S3中的2个变量赋值给ρ,实现ρ∧C3⟹wp(S3,ρ),显然第3个条件子句成立. (iii)证明后置断言R在循环终止时必须为真. ρ∧┐ (flag∧(┐(q=%)∨┐(S=[])))⟹AR≡ρ∧(┐flag∨((q=%)∧(S=[])))⟹fbalance(T)=∀(a:a∈HLay(T):abs(Ldepth(a.l)-Ldepth(a.r))≤1)≡ρ∧(┐flag∨(flag∧(q=%)∧(S=[])))⟹fbalance(T)=∀(a:a∈HLay(T):abs(Ldepth(a.l)-Ldepth(a.r))≤1)≡HLay(T)=X↑[q.d]↑F(S↑[q.l]↑[q.r])∧flag=∀(a:a∈X:isbalance(a)=true)∧(flag∧(q=%)∧(S=[]))⟹fbalance(T)=∀(a:a∈HLay(T):abs(Ldepth(a.l)-Ldepth(a.r))≤1)≡HLay(T)=X∧true=∀(a:a∈X:isbalance(a)=true)∧(flag∧(q=%)∧(S=[]))⟹fbalance(T)=∀(a:a∈Lay(T):abs(Ldepth(a.l)-Ldepth(a.r))≤1)≡true∧true=∀(a:a∈X:isbalance(a)=true)∧(flag∧(q=%)∧(S=[]))⟹fbalance(T)=∀(a:a∈HLay(T):abs(Ldepth(a.l)-Ldepth(a.r))≤1)≡true. (iv)循环的终止性显然成立. 至此, 完成了此程序的正确性证明. 本实验室研究团队已经开发了一个“Apla到C++程序自动生成系统”[7],可以实现Apla到C++程序的自动转换,实现算法程序的机器无关性.“Apla到C++程序自动生成系统”总体结构如图2所示. 图2 “Apla到C++程序自动生成系统”总体结构图 通过“Apla到C++程序自动生成系统”,可将推导并形式化证明的Apla算法程序作为源语言,自动生成对应的C++可执行程序[22],本文的实例均可自动生成对应的C++可执行程序,以判断平衡二叉树为例(见图3).“Apla到C++程序自动生成系统”集词法分析、语法分析、语义一致性分析、转换、编译、运行为一体.Apla语言中抽象数据的操作均基于简单数据类型及其操作,为了转换一些简单数据类型及其操作,于是,先构造了一个简单的程序转换系统,称为“核心转换器”,然后通过抽象数据类型的操作推导得到Apla程序,再用“核心转换器”转换为C++程序,作为相应的C++可重用部件库中的操作,最后通过这种方式C++可重用部件库的正确性就得到了保证.由此,Apla算法程序自动生成C++程序的正确性也得到了保证,最终实现了从抽象规约到具体的可执行程序的完整求精过程[9]. 图3 Apla到C++程序自动生成系统生成判断平衡二叉树的C++程序 图3代码为判断平衡二叉树非递归算法的Apla程序,通过左边的Apla代码自动生成对应的C++可执行程序如下: flag=true; do { if (flag && (!(q.Equa(tempTree0.SetEmpty0))||!(S.Equal(tempList1.SetEmpty0)))) { if ((q!tempTree0.SetEmpty0)&&(isbalance(q)==true)){ flag=true; X.Copy(X.Concat(OneitemList(q.Data0))); S.Copy(S.Concat(OneitemList(q.Left0).Concat(OneitemList(q.Right0)))); q.Copy(tempTree0.SetEmpty0); } else if ((q!=tempTree0.SetEmpty0) && (isbalance(q)==false)) { flag=false; X.Copy(X.Concat(OneitemList(q.Data0))); S.Copy(S.Concat(OneitemList(q.Left0).Concat(OneitemList(q.Right0)))); q.Copy(tempTree0.SetEmpty0); } else if ((q.Equal(tempTree0.SetEmpty0)) &&!(S.Equal(tempList1.SetEmpty0))) { q.Copy(S.Get(S.h)); S.Copy(S.Sublist(S.h+1,S.t)); } } else. 输入10个无序的整数序列,并将其构成二叉排序树,对二叉排序树进行判断是否为平衡二叉树(见图4). 图4 构建二叉排序树 通过验证,自动生成的C++程序是正确的.“Apla到C++程序自动生成系统”将预定义的组合数据类型(集合、列表、二叉树、图、关系数据和其他预定义的数据类型)以ADT的形式进行封装,并且可以用作标准数据类型,这极大地提高算法和程序的开发效率. 本文通过对二叉树类问题进行分划,寻找递推关系,对求解序列的递推关系为队列这类问题,给出推导和形式化证明策略.探索二叉树队列关系问题非递归算法的循环不变式之间的共性和特性,发现很多二叉树队列关系问题都是可以基于层次遍历二叉树和求二叉树深度这2个算法的功能加以实现,由此,可将二叉树队列关系问题分为3类派生问题.本文对派生问题代表进行推导,得出递推关系表达式和循环不变式,由此导出非递归Apla算法,再用Dijkstra-Gries标准程序证明法证明算法的正确性,最后使用“Apla到C++程序自动生成系统”自动生成C++可执行程序,实现了从抽象规约到具体的可执行程序的完整求精过程.相比国内外现有研究,本文具有如下特点: 1)提出了二叉树队列关系问题非递归算法推导及形式化证明策略.主要对3种输出结果问题对应地提出了3种开发循环不变式策略,并根据循环不变式之间的共性和特性,构造一个二叉树队列关系问题通用循环不变式模板,使求解二叉树队列关系问题更具有针对性. 2)成功地推导和形式化证明了一系列二叉树队列关系问题非递归算法.在推导过程中,基于层次遍历二叉树和求二叉树深度这2个算法的功能,将推导二叉树队列关系问题分为3类派生问题.这便于派生问题更准确、更便捷地推导和形式化证明. 3)使用开发的“Apla到C++程序自动生成系统”,对原算法程序规约进行了一系列的求精变换步骤.每一步都减少了一定的抽象程度或增加了一定的程序可执行性,并最终得到相应的C++可执行程序.该程序实现了从抽象规约到具体的可执行程序的完整求精过程,这极大地提高了算法和程序的开发效率和可靠性. 本文的研究提升了开发共性算法程序的高效性和有效性,对寻找各种二叉树队列关系问题非递归算法的循环不变式指明了新的方向,对非线性数据结构算法程序的推导及形式化证明具有指导意义.2.2 改进循环不变式
2.3 二叉树队列关系问题通用循环不变式模板
2.4 预定义ADT
2.5 二叉树队列关系问题的3类派生问题
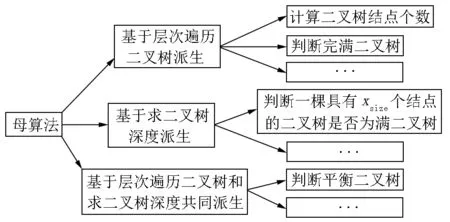
3 二叉树队列关系问题非递归算法推导
3.1 母算法
3.2 形式推导实例
4 二叉树队列关系问题非递归算法形式化证明
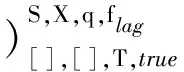
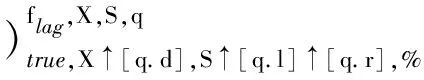
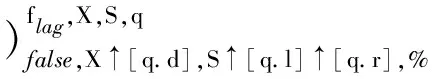
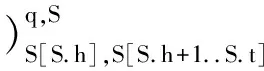
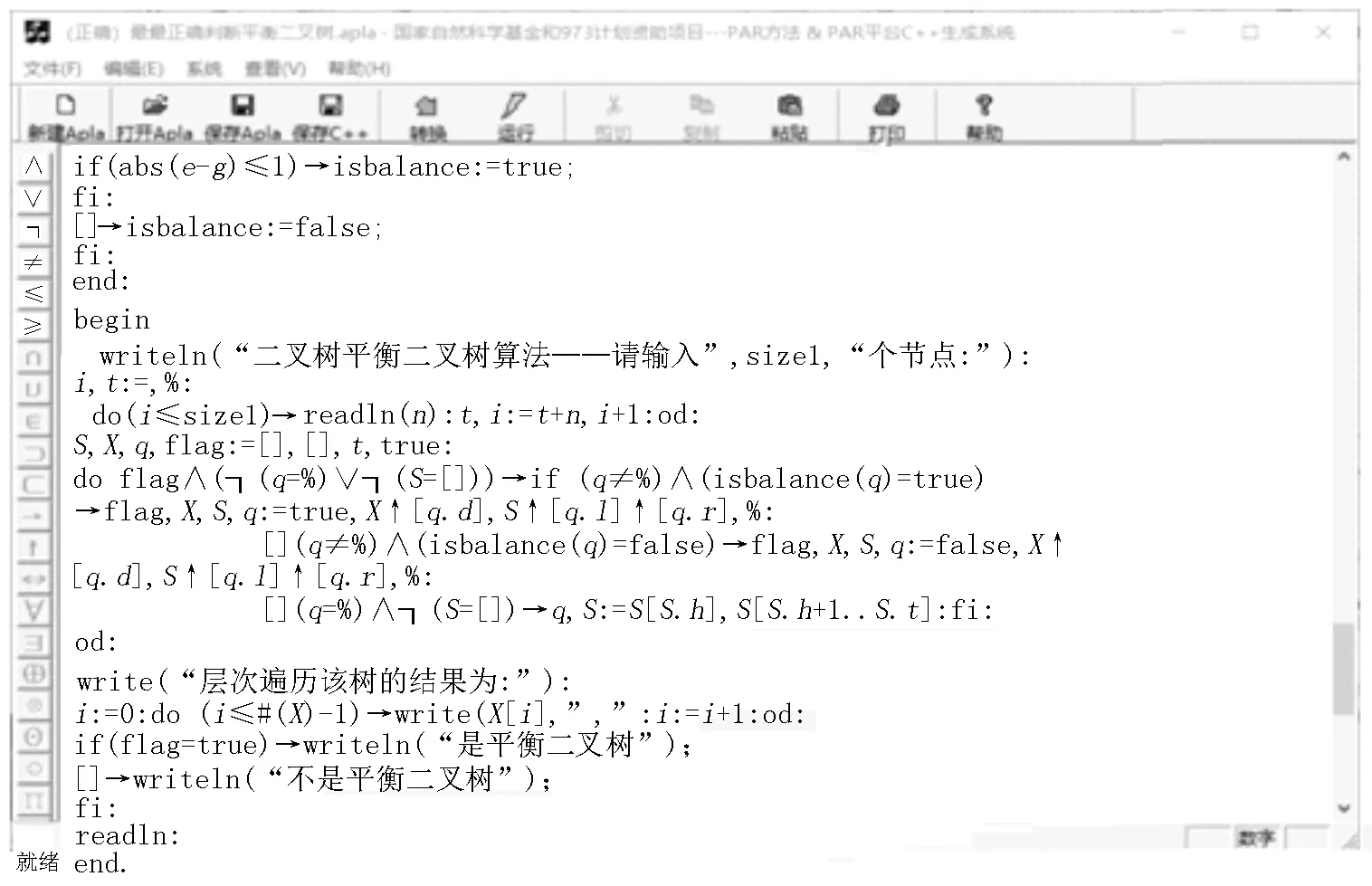
5 二叉树队列关系问题C++程序的自动生成

6 结束语

