基于双指数跳跃-扩散过程的欧式一篮子期权定价

杨 芮,张艳慧*,温 伟

(1.北京工商大学数学与统计学院,北京 100048;2.北京工商大学经济学院,北京 100048)

0 引言

一篮子期权是一种多资产期权，是在金融衍生品市场上交易最为活跃的新型期权之一，其标的资产是一组或一篮子商品、证券或货币，这些资产可任意组合，根据投资者的需求做出适当的组合来对冲风险，因此一篮子期权越来越受到投资者的青睐.

1900年L. Bachelier[1]将随机游走引入金融市场，提出了关于标的资产价格的随机模型,这标志着期权定价理论的问世.1973年F. Black等[2]假设股票价格是连续的扩散过程并且服从几何布朗运动，提出了著名的Black-Scholes期权定价模型.实证分析[3]表明:在Black-Scholes期权定价公式中资产价格的假设和实际的金融市场存在不符，重要信息的出现往往会导致资产价格发生跳跃.R.C. Merton[4]在扩散过程中加入跳跃，假设资产价格是由几何布朗运动和泊松过程共同驱动的，并且跳跃幅度服从正态分布，但很难得到解析解.文献[5]提出了双指数跳跃-扩散模型，跳跃以泊松过程到达，跳跃幅度用双指数分布刻画，即资产价格由一个连续变动的几何布朗运动和一个不连续的、跳跃幅度服从双指数分布的泊松跳过程组成.双指数跳跃-扩散模型解释了非对称峰度特征和“波动率微笑”现象，又因为指数分布的无记忆性，所以利率衍生品、路径依赖型期权等存在解析解.

目前，研究一篮子期权定价的常用方法有求解偏微分方程法[6-7]、Monte Carlo模拟法[8-9]和特征函数法[10].J.M. Harrison等[11-12]提出了一种求解金融衍生品的定价方法——鞅定价方法，他们证明在一定条件下，市场无套利等价于存在等价概率鞅测度，使得市场中任意资产过程在此测度下为鞅.文献[13-15]对用鞅求解期权价格作了进一步研究.文献[16-18]研究了利用鞅求解在跳跃-扩散模型下的单资产期权定价问题.

本文拟建立具有相关性的多维双指数跳跃-扩散模型，并利用鞅定价方法得到关于双指数跳跃-扩散模型的一篮子欧式期权定价公式，可用于实证处理一篮子期权的定价问题.

1 多维双指数跳跃-扩散过程

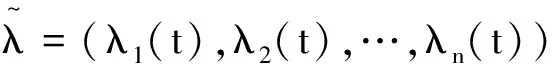
设Si(t)是第i个风险资产的价格(i=1,2,…,n),它满足随机微分方程

其中μi为资产Si(t)的预期收益率,σi是波动率,ρki为风险资产Si(t)和Sk(t)的相关系数,满足

W1(t),W2(t),…,Wn(t)是互相独立的标准布朗运动,Vi,j(j=1,2,…,N(t))是独立同分布的非负随机变量.

设Yi=lnVi是跳跃幅度,双指数跳跃-扩散模型的跳跃幅度分布函数为

fYi(y)=piηi,1e-ηi,1yI{y≥0}+qiηi,2e-ηi,2yI{y<0},ηi,1>1,ηi,2>0,

其中pi(>0)表示资产价格Si(t)向上跳跃的概率,qi(>0)表示资产价格向下跳跃的概率,pi+qi=1.ηi,1>1是为了保证E(Vi)<∞和E(Si(t))<∞,本质上是要求平均向上跳的尺度不能超过100%,即

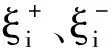
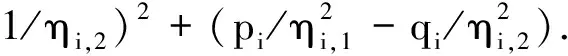
由于市场无套利，风险中性测度存在，市场不完全，风险中性测度不唯一，因此可选一个特殊的风险中性测度P,使得市场内所有资产的折现期望在新的测度P下为鞅[20].在该风险中性测度P[5]下有

(1)

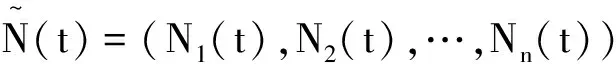
pi≥0,qi≥0,pi+qi=1,λi>0,ηi,1>1,ηi,2>0,ζi=E(eYi-1)=piηi,1/(ηi,1-1)+qiηi,2/(ηi,2+1)-1.

引理1当资产价格满足随机微分方程(1) ，则资产价格的方程为

(2)

证证明方程(2)满足随机微分方程(1).资产价格Si(t)的连续随机过程为

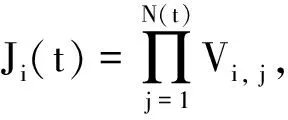
(3)

在第j次跳时,Ji(t)=Ji(t-)Vi, j,则

Ji(t)-Ji(t-)=Ji(t-)(Vi, j-1).

方程Ji(t)-Ji(t-)=Ji(t-)(Vi, j-1)在非跳跃时刻也成立,故

(4)

由关于跳过程的Ito公式可知

(5)

Ji(t)是纯跳过程，而Xi(t)连续，故(Xi,Ji)(t)=0,将式(3)和式(4)代入式(5)得

其微分形式为

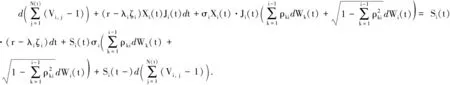
引理1得证.

2 欧式一篮子期权定价公式

基于第1节建立的双指数跳跃-扩散模型,本文得到如下主要结果.

定理1若资产价格Si(t)(i=1,2,…,n)服从双指数跳跃-扩散模型(1)，则欧式一篮子看涨期权价格C(t,S1(t),S2(t),…,Sn(t))为

其中Φ(x)为标准正态分布的分布函数,λ为n个资产的跳跃强度,

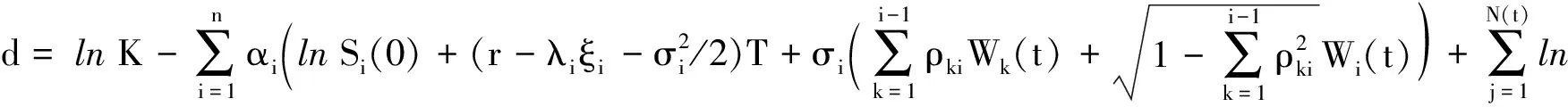
证在概率测度P下，贴现看涨期权价格是鞅，即一篮子看涨期权价格C(t,S1(t),S2(t),…,Sn(t))满足

C(t,S1(t),S2(t),…,Sn(t))=E(e-r(T-t)·

记

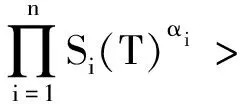
整理得

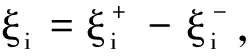
则X服从正态分布,且

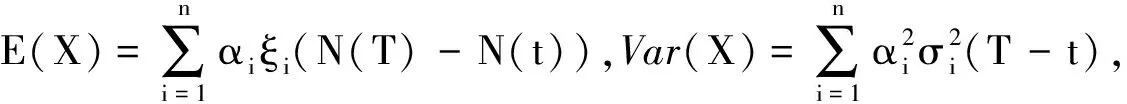
(6)

由全概率公式知,

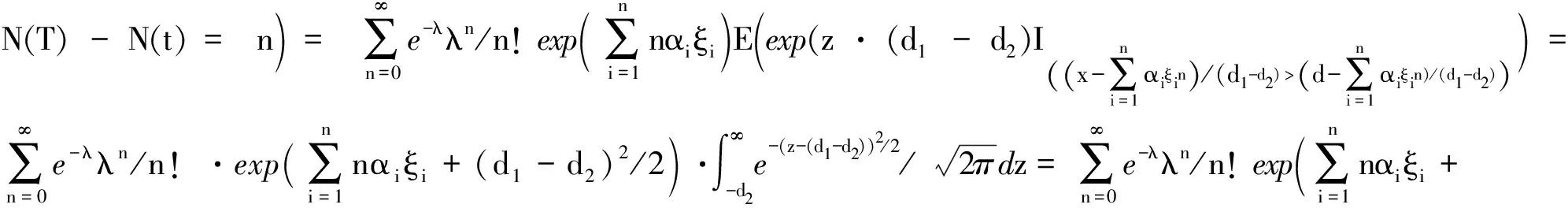
(7)

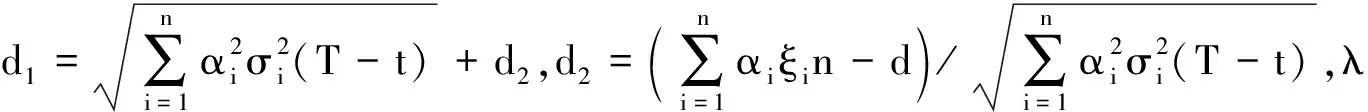
定理1得证.

定理2若资产价格Si(t)(i=1,2,…,n)服从双指数跳跃-扩散模型(1),则欧式一篮子看跌期权价格P(t,S1(t),S2(t),…,Sn(t))为

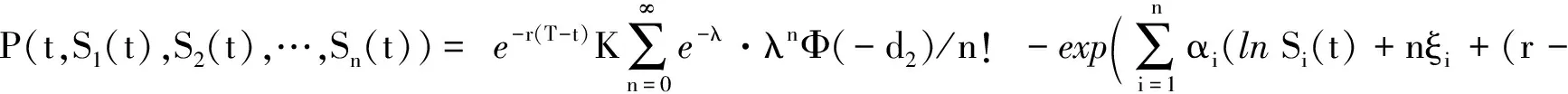
其中Φ(x)为标准正态分布的分布函数,λ为n个资产的跳跃强度,d1和d2如定理1定义.

证在概率测度P下，贴现看跌期权价格是鞅，即一篮子看跌期权价格P(t,S1(t),S2(t),…,Sn(t))满足

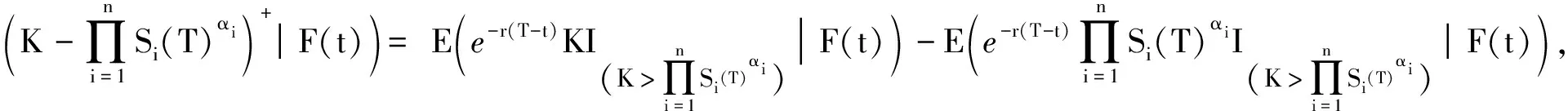
所以

(8)

由全概率公式知,

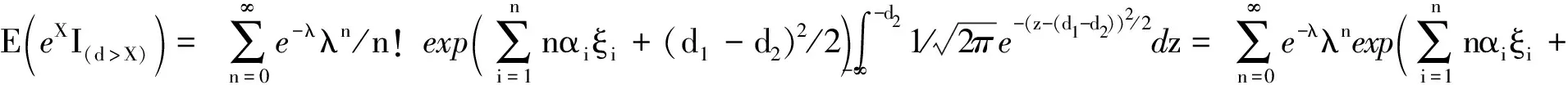
(9)

将式(9)代入式(8)，整理得

定理2得证.

注1当n=1时，风险资产价格服从1维双指数跳跃-扩散模型，定理1和定理2为基于双指数跳跃-扩散模型的单资产欧式期权价格公式，即风险资产价格S(t)满足随机微分方程

欧式看涨期权和欧式看跌期权在到期日时的收益分别为(S(t)-K)+和(K-S(t))+,则欧式看涨期权价格为

欧式看跌期权价格为

其中Φ(x)为标准正态分布的分布函数,

注2当N(t)=0时 ，风险资产价格服从多维Black-Scholes模型，定理1和定理2为基于Black-Scholes模型的一篮子欧式期权价格公式，即风险资产价格Si(t)满足随机微分方程

基于Black-Scholes模型的一篮子欧式看涨期权价格为

基于Black-Scholes模型的一篮子欧式看跌期权价格为

其中Φ(x)为标准正态分布的分布函数 ，

3 结论

Black-Scholes期权定价公式是基于连续变化的风险资产价格的，而跳跃-扩散模型是基于不连续市场的期权定价模型的,它更适应价格突变对资产价格的影响，因此在资产实价问题中研究了跳风险因素.双指数跳跃-扩散模型在解决路径依赖型期权方面更易于处理，容易得到解析解，定价结果接近实际.

由于一篮子期权的资产之间是存在相关性的，本文不是将双指数跳跃-扩散模型平行推广到多维，而是利用多维双指数跳跃-扩散过程得到了具有相关性的标的资产满足双指数跳跃-扩散过程的价格公式.本文研究在资产价格服从双指数跳跃过程下一篮子欧式期权的定价问题，它是通过测度变换最后利用鞅定价方法得到的.在期权定价中，鞅测度的引入对于掌握定价方法、优化组合、降低风险都是非常重要的，可将期权定价的明确评估简单化.