一种协同问答信号配对规则提取方法*

龙慧敏，余 博，冯志斌

(1.中国西南电子技术研究所，成都610036；2.中国人民解放军93114部队，北京100195；3.中国人民解放军93147部队，重庆402760)

0 引 言

敌我识别(Identification of Friend or Foe,IFF)、塔康等协同式无线电问答系统提供目标识别、空中导航等功能，在信息化战争中得到了广泛应用[1-2]。系统通过询问应答构成复杂的信号通联关系[3]。问答信号通联关系分析是利用信号处理与数据分析技术对无线电信号侦察传感器获取的询问应答信号数据进行分析，实现询问-应答信号配对，提取询问、应答间的通信连接关系，对分析无线电问答系统的工作模式、识别网络拓扑结构及其关键节点，获取目标信息、掌握目标态势进而分析战场态势有重要的价值和意义[4-5]。

问答信号配对是通联关系分析的首要环节。问答信号配对的传统方法可分为两类：一类是基于问答内涵信息实现通联配对[6-7]；另一类是基于通联规则提取通联配对关系[8]。上述方法需要掌握系统工作机制和通信协议，对先验知识依赖程度较高。随着加密通信和新型通信不断发展，内涵解析困难、先验知识缺乏，上述两类方法实现难度剧增。因此，在通信内涵难以获取、通信协议未知或部分已知条件下实现问答配对已成为信号通联关系分析技术发展的重要方向。文献[9-10]利用定频/跳频通信信号电磁频谱特征的相似性，对电磁频谱监测获得的信号电平、时间和频率进行统计聚类，获取通信网络通联关系。文献[11]采用端到端的识别方法，构建残差神经网络模型，通过频谱监测数据分类实现了无线通信电台的通联关系识别。上述方法在缺乏先验知识的情况下，利用电磁频谱监测数据，通过统计聚类、神经网络分类等方法，判别电台间是否存在通联关系，但并不能在多电台条件下实现无线通信电台间通信信号的一一配对并提取出明确的通联规则知识。目前尚未在公开文献中查询到问答信号通联配对规则提取相关的技术。

本文基于被动侦察手段获取的协同问答信号侦察数据，提出了一种通过询问应答信号出联时序模式挖掘，提取询问应答信号通联配对规则，实现询问应答信号一一精确配对的方法，并通过仿真和实侦数据验证了方法的有效性。

1 信号通联模式原理分析

协同问答系统需遵循一定的工作机制和通信协议[12]。通常情况下，询问方以特定频率发射携带询问信息、具有特定格式的询问信号，传输到达应答方，应答方接收处理询问信号后，根据协议采用相应频率发射带有应答信息的、具有一定规格的应答信号。问答信号在信号发射时间、信号频率、信号模式、信号特征参数(长度、间隔、调制方式、调制速率)等方面具有符合系统工作机制体制和通信协议的规律，表现为图1上半部分所示的模式。

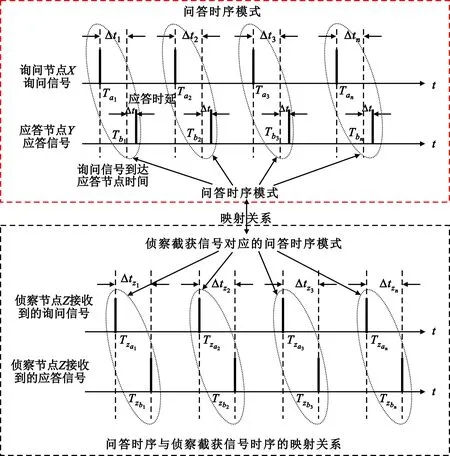
图1 询问应答信号通联模式

设询问节点X与应答节点Y存在问答关系，节点X在Ta1时刻发出某模式询问信号a1，a1在空中传播Δt1后于Tb1时刻到达节点Y，节点Y经过应答时延Δt后回复对应模式应答信号b1，a1和b1构成一组通联信号对；当节点X与Y之间存在N次通信时，节点X在Ta==(Ta1,Ta2,…,TaN)时刻发出的信号形成信号时间序列A=(a1,a2,…,aN)，节点Y则在Tb==(Tb1,Tb2,…,TbN)的回复信号形成信号序列B=(b1,b2,…,bN)，那么A与B之间存在(a1与b1,a2与b2,…,aN与bN)N组通联信号对，N组通联信号对之间形成应答时间差序列ΔT=Tb-Ta=(Δt1,Δt2,…,ΔtN)。在相同模式下，通联信号对之间信号特征参数向量相似，应答时间差应属于同一特定数值范围。

从数据分析角度，通联信号对a1和b1是信号数据集中的一个数据项集合，即事件a1发生后时间间隔Δt1内发生事件b1[13]。若存在N次通联，在信号序列A与B中存在多次出现的、信号特征相近、按时间排列的事件(ai,bi,Δti)组合，事件ai发生之后Δti时间内发生事件bi(i=1,2,…,N)，该组合即信号通联频繁模式。

设侦察节点Z能够接收X与Y双方的信号，信号侦察数据序列与问答信号序列存在如图1下半部分所示的映射关系。实侦条件下的侦察数据序列包含多种通联映射模式。

侦察节点Z截获询问节点X和应答节点Y发出的信号，获得包含节点编号、节点位置、信号频率、到达时间、脉冲宽度、脉冲间隔、调制方式等要素在内的询问和应答信号侦察数据；通过侦察数据序列分析，识别询问和应答侦察数据时空序列中的频繁模式，反向推演被侦察的询问应答节点间通联模式，提取问答双方信号存在的特征模式和应答时延Δt，生成询问应答节点的信号配对规则。

2 信号配对规则挖掘

利用被动侦察手段所截获的多节点通信信号时间序列构造训练样本集和测试样本集，采用频繁模式挖掘方法在训练样本集寻找多个时间序列间的频繁项集，计算节点间信号的关联性，根据存在强关联性的信号对的特征，挖掘信号配对的可能规则，并利用测试样本集对挖掘出的配对规则进行验证，提取测试样本集中存在的节点间的通联关系。对于未知通信协议的通信系统，该方法基于数据驱动模式从信号侦察数据中发掘配对规则，可实现系统通联关系的有效提取。

本文提出的问答信号配对规则挖掘流程如图2所示。

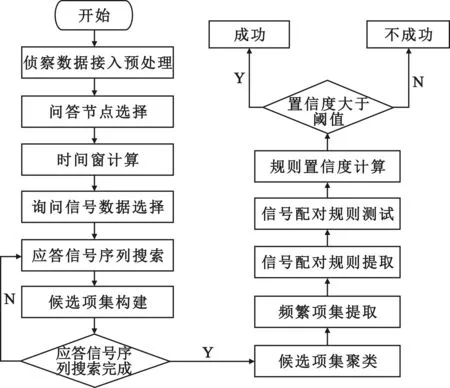
图2 问答信号配对规则挖掘流程

2.1 信号数据序列预处理

信号侦察数据具有不完全性、噪声性和随机性，需要错误数据剔除、时间同步、数据类型转换，为下一步的处理做准备。

2.2 候选项集构建

设Z侦获节点X询问信号参数时间序列为SX=(Ca1,Ca2,…,CaI)，Cai为第i个询问信号特征参数向量，侦察时间为Tza=(Tza1,Tza2,…,TzaI)；应答节点Y信号时间序列为SY=(Cb1,Cb2,…,CbJ)，Cbj为第j个应答信号特征参数向量，侦察时间为Tzb=(Tzb1,Tzb2,…,TzbJ)。

搜索集合SX和SY，交叉构建询问应答信号2-项候选项集(Cai,Cbj)。理论上SX和SY间成对出现的信号对均可作为2-项候选集，但这样产生的候选集规模太大且不符合信号传播原理。本文基于无线电信号传播原理，根据询问、应答和侦察节点位置信息设置一定大小时间窗TW，在SY序列中搜索Cai出现后TW范围内的Cbj构建2-项候选集，降低候选集规模，提高合理性和搜索效率。

询问节点X、应答节点Y与侦察节点Z位置关系如图3所示。

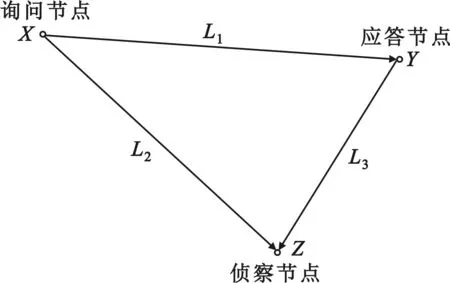
图3 节点间位置关系

根据节点间位置关系和信号传播特性，Z收到Y询问信号与X应答信号的时间差ΔTz=(L1+L3-L2)/c+Δt，其中c为电磁波传播速度。根据三角形边的关系，可得出Δt<ΔTz<(2L3/c+Δt)。

根据上述分析，时间窗设置原则如下：

(1)时间窗TW起始时间TWS>Tzai;

(2)时间窗TW理论长度TWL>2L3/c，受信号直线传播和侦察节点作用范围的影响，通常L3<600 km，因此TWL≤4 ms；

(3)时间窗过窄易导致搜索不到可配对的项集，而过宽则易产生如图4所示的模糊配对问题。本文利用询问和应答节点定位信息，设置适当的时间窗，减少配对失败和配对模糊问题。

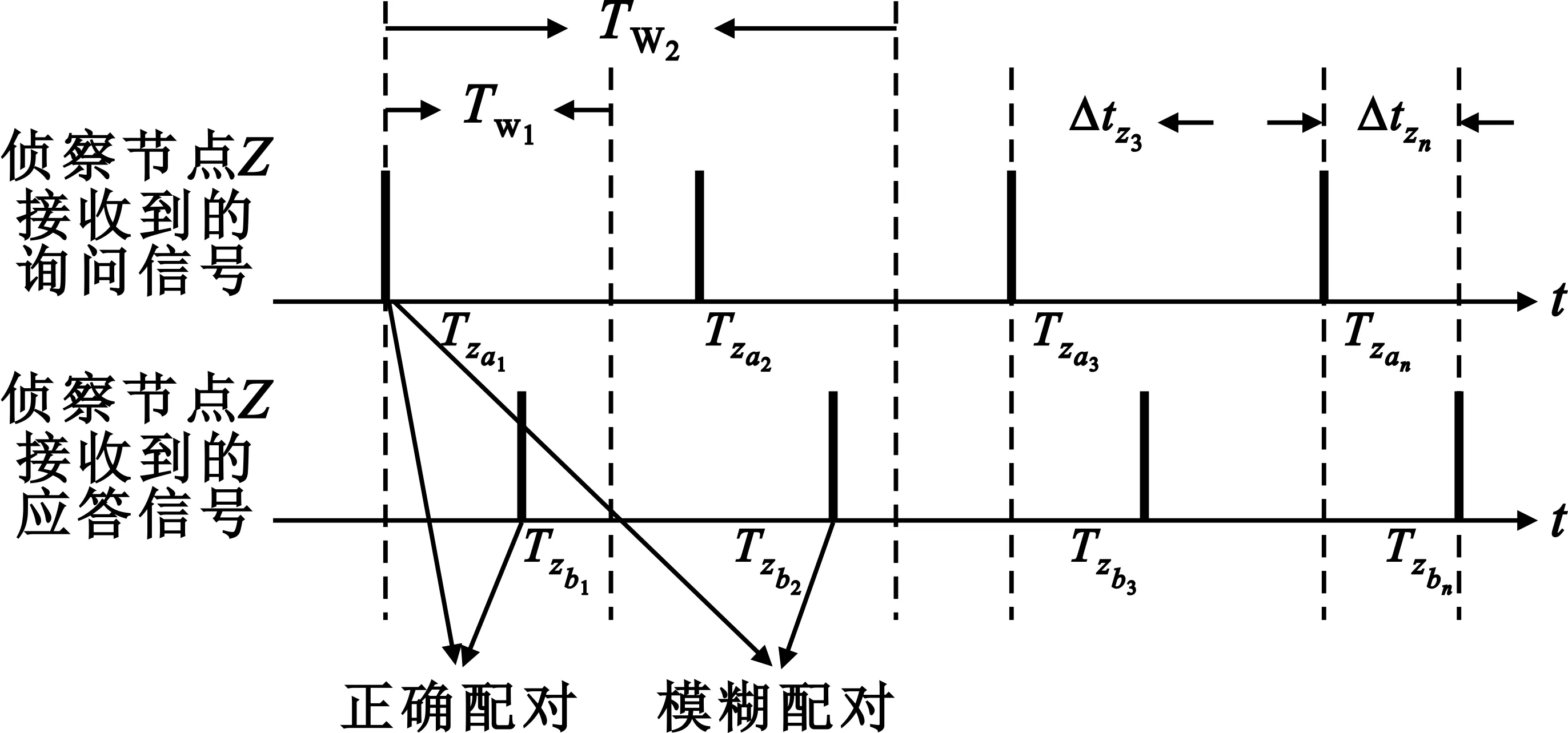
图4 模糊配对问题

询问应答2-项候选项集生成流程如下：

Step1 在序列SX中选择询问Cai，读取时间Tzai。

Step2 在序列SY中Tza1+TWL时间范围内搜索应答Cbj，依次与Cai组成候选2-项集，并计算Cai与Cbj的时间差Δtij。

Step3 当j=M，SY搜索完成，变量i+1，重复Step 1和Step 2。

Step4 当变量i=N，SX序列搜索完成，形成全部2-项候选集C2=(Cai,Cbj|Δtij)，其中i=1,2,…,N;j=1,2,…,M。

2.3 频繁项集挖掘

根据候选项集询问应答信号特征，计算C2中各候选项集出现次数，设最小支持度为s，出现次数超过s的候选项集即为频繁项集P，M为计算出的频繁项集个数。

Pm=(Cxm,Cym|Δtsm),m=1,2,…,M。

在复杂电磁环境下，问答信号密集，难以预知数据类别；同时，受信号测量参数误差影响，特征向量分布呈现柱状/椭圆状特点，因此本文选用基于密度的DBSCAN(Density-based Spatial Clustering of Applications with Noise)方法对C2进行聚类。在实际使用中，可根据数据特点优化选择聚类算法。

经过聚类后，得到K个类别，每一类都是由rk个相似信号对特征向量组成集合，也可以用rk行的矩阵表示，1≤k≤K；计算每个类别的支持度sk=rk/M，若sk>s则表示该类为通联信号对频繁项集Pl，1≤l≤L，L为计算出的频繁项集的个数，L≤K。

2.4 信号配对规则提取

获得频繁项集后，通过提取频繁项集对应的问答信号特征参数及时间差，建立问答信号配对规则，包括信号时序配对规则和信号特征匹配规则。

2.4.1 信号时序配对规则提取

对频繁项集中询问和应答信号对之间到达时间差Δtm序列进行统计，根据询问节点、应答节点和侦察节点的位置关系计算应答节点收到询问信号时刻Tx和发出应答信号时刻Ty之间的时间延迟Δτm序列，统计时间延迟Δτm序列的均值mean(Δτ)、最大值max(Δτ)和最小值min(Δτ)。

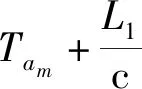
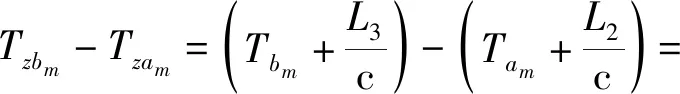
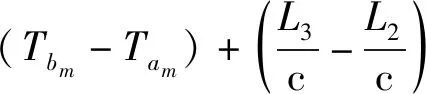
(1)

(2)

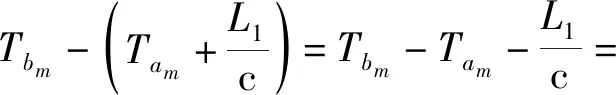
(3)

问答信号时序配对规则表达为Δτ′，如式(4)所示：

(4)

式中：Δτc=(max(Δτ)-min(Δτ))/2。

2.4.2 信号特征匹配规则提取

以矩阵形式表示通联信号对频繁项集Pl：

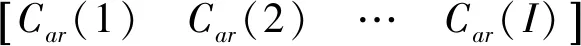
频繁项集Pl矩阵每一列代表信号一类特征参数的值。计算频繁项集矩阵中每个列向量均值、最大值和最小值，得到列向量均值集合E(PL)、最大值集合max(PL)和最小值集合min(PL)：

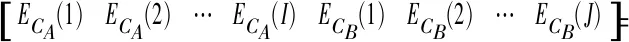
式中：ECA(i)表示询问信号第i个特征向量的均值，ECB(j)表示应答信号第j个特征向量的均值；ECA表示询问信号特征向量的均值集合，ECB表示应答信号特征向量的均值集合；maxCA(i)表示询问信号第i个特征向量的最大值，maxCB(j)表示应答信号第j个特征向量的最大值；minCA(i)表示询问信号第i个特征向量的最小值，minCB(j)表示应答信号第j个特征向量的最小值；1≤i≤I，1≤j≤J。

(5)

ΔCA(i)=(maxCA(i)-minCA(i))/2，

(6)

(7)

ΔCB(j)=(maxCB(j)-minCB(j))/2。

(8)

2.5 规则测试与可信度评价

通过上述方法提取的规则成功通过测试后可作为可信规则。规则测试流程如图5所示，接入询问应答测试样本后，分别提取询问、应答信号特征参数，根据到达时间、节点位置等信息计算询问、应答发射时间差；分析发射时间差与时序配对规则、测试样本特征与特征匹配规则的符合性，若两者均满足规则要求，则判定询问应答匹配；若不满足其一或两者均不满足，则判定询问应答不匹配。

图5 规则测试流程

在上述测试基础上，本文采用置信度、配对正确率以及配对虚警率评价规则的可信度。

2.5.1 规则置信度

问答信号配对是典型的正关联问题[14]，规则置信度表征询问节点发射某特定模式询问信号后，在L1/c+Δτ′时间范围内出现应答信号的概率。其计算步骤如下：

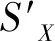
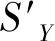
Step3 统计CA出现后L1/c+Δτ′的时间范围的相似向量后搜索到CB的相似向量的总数量NCAB。

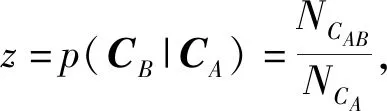
Step5 将置信度z与置信度阈值进行比较，若置信度z大于置信度阈值zt，则判定规则可信，否则判定规则不可信。

本文依据正关联置信度计算方式，采用式(9)计算置信度范围下限，作为置信度阈值。

(9)

2.5.2 配对正确率

配对正确率是指应用配对规则后信号正确配对的比例，即正确匹配数量与真实的信号通联数量的比值，其计算方式如式(10)所示：

配对正确率=正确配对数/真实通联数。

(10)

2.5.3 配对虚警率

配对虚警率是指应用配对规则后，信号模糊配对的比例，即模糊匹配数量与真实信号通联数量的比值，即其计算方式如式(11)所示：

配对虚警率=模糊配对数/真实通联数。

(11)

在真实通联数已知的条件下，可采用上述三种指标对规则进行综合评价；在实侦条件下，难以获取真实通联数量，通常采用置信度进行评价。

2.6 算法复杂度分析

配对规则挖掘算法分为规则提取和规则应用两部分，其中规则提取部分复杂度主要受2-项候选集构建和项集聚类复杂度的影响，规则测试部分则受配对搜索方法的影响。本文重点探讨规则提取部分算法复杂度。

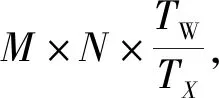
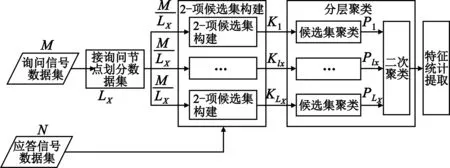
图6 算法复杂度分析示意图

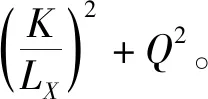
那么，加上特征统计后，规则提取算法的计算次数可表示为

(12)

3 实验与分析

3.1 基于仿真数据集的算法验证

3.1.1 仿真数据集构建

本文依据典型平台目标、IFF系统以及侦察装备工作机制及功能性能参数建立实体数字化模型，编辑想定场景，根据目标机动航迹、IFF系统实时发射功率及方向、侦察灵敏度及实时侦察方向，充分考虑平台机动、信号传播、测量误差等因素，生成包括信号频率、脉宽、脉冲间隔、脉冲到达时间、调制方式、调制速率、位置等要素的仿真数据集。

场景1如图7(a)所示，设置询问、应答和接收节点各1个，询问节点以三种模式(1/2/3)进行询问(询问PRI为3.33 ms)，应答节点收到询问信号后应答，仿真时长5 s，生成长度1 501的询问和应答序列。场景2如图7(b)所示，设置询问节点3个，应答节点4个，接收节点1个。询问节点1采用四种模式(1/2/3/4)、询问节点2采用三种模式(1/3/4)、询问节点3采用两种模式(3/4)询问，询问PRI分别为2.5 ms、4 ms和5 ms，仿真时长1 s，产生850条询问和3 400条应答信号数据。应答延迟设置为2.5 μs(依据IFF系统特点设置)，信号脉宽、脉冲间隔、到达时间等特征参数测量误差设置为均值0.2 μs的随机数，模式支持度阈值设置为0.1。

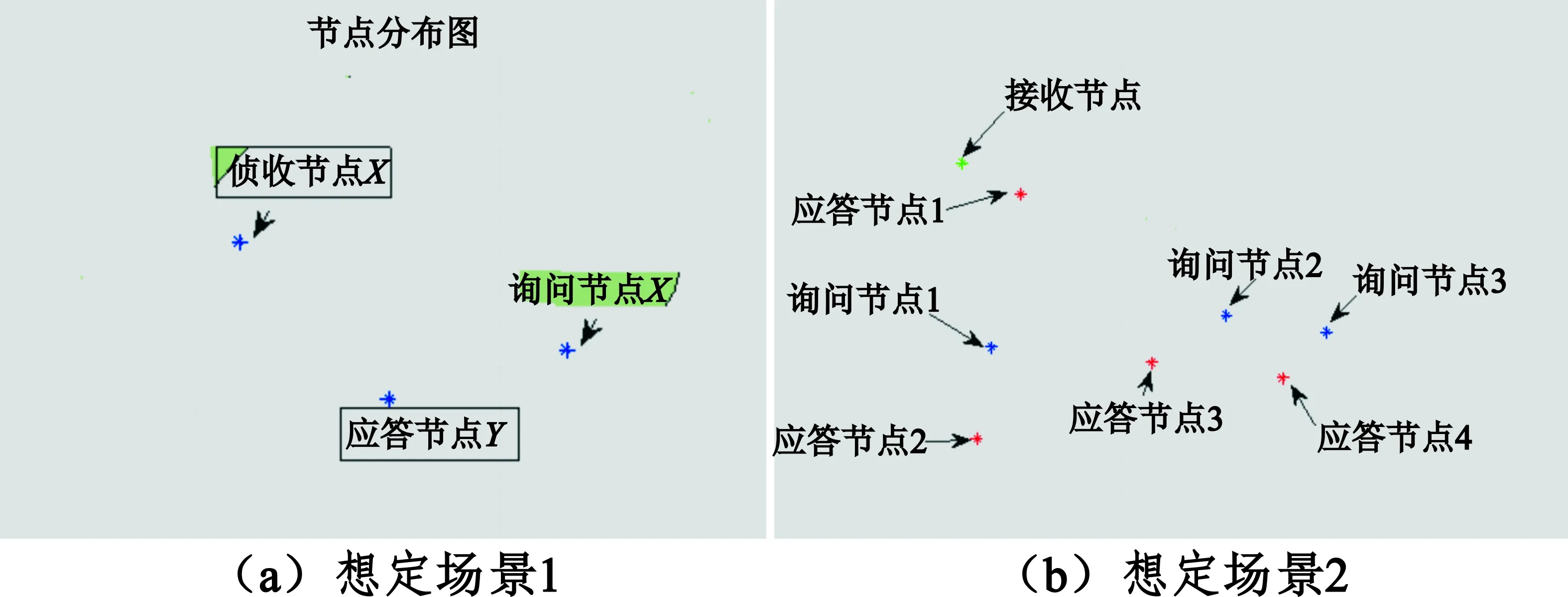
图7 仿真场景图

信号特征设置如表1所示。

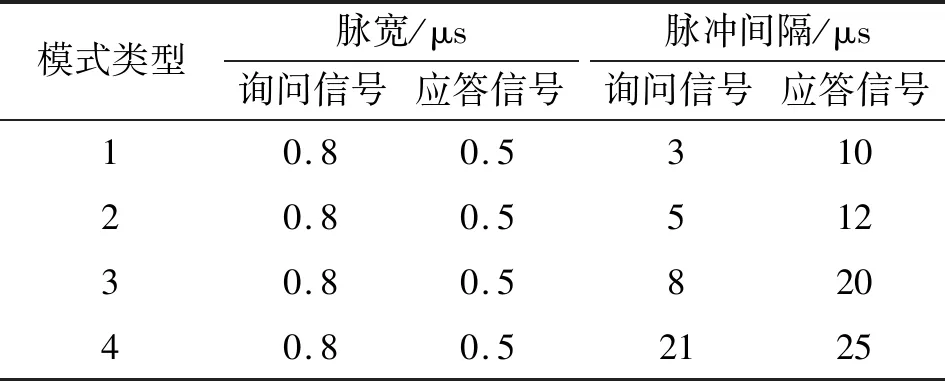
表1 信号特征(仿真值)

3.1.2 信号配对规则提取仿真

取仿真数据集中前80%的数据为训练样本集，剩余20%数据为测试样本集，训练和测试样本集同分布。对仿真训练样本集做2-项候选项集提取，并采用DBSCAN算法对2-项候选项集进行特征聚类，形成的聚类结果如图8所示。

(a)场景1候选项集聚类结果

如图8(a)所示，场景1包含三种信号配对类型，配对类型项集数与支持度情况如表2所示。

表2 场景1配对类型支持度

按照式(1)提取问答信号时序规则：

Δτ′∈(2.5013±0.4987)μs。

场景1提取的三种类型问答信号特征匹配规则如表3所示。

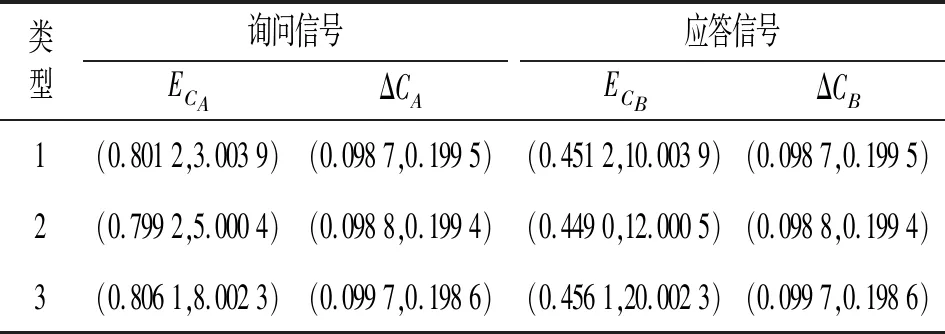
表3 场景1信号特征匹配规则

场景2仿真训练样本集共生成2 785个候选项集，聚类获得如图8(b)所示的6种配对类型，各类数量与支持度如表4所示。

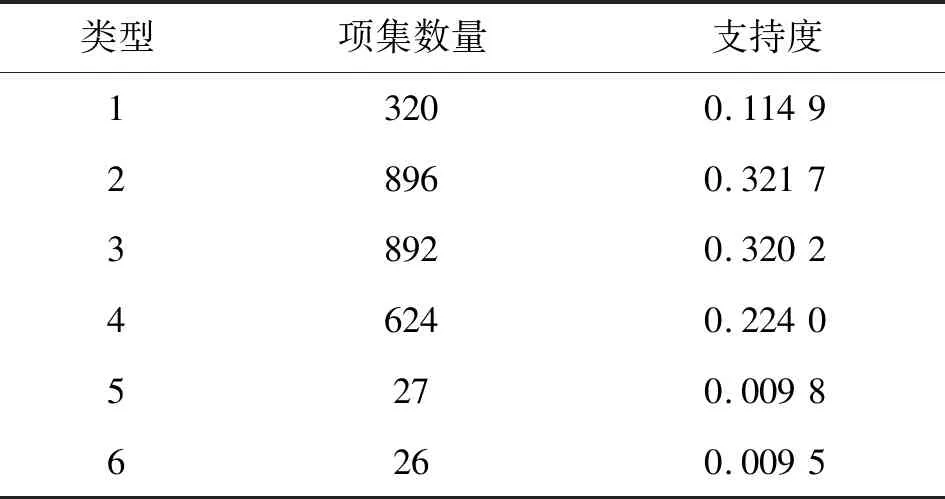
表4 类型支持度

如表4所示，本文所提方法在仿真训练样本集中挖掘出6种配对类型，其中2种支持度低于阈值，不满足频繁项集条件。四种类型对应时间差如表5所示。

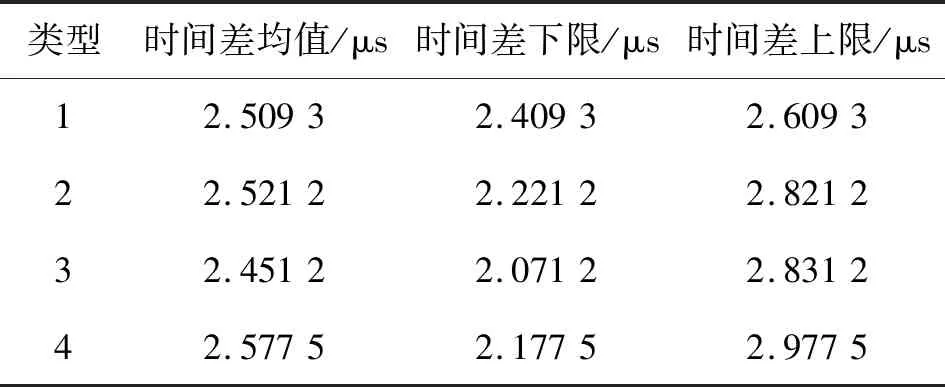
表5 场景2问答时间差

取时间差下限和上限的最大值，提取时间差规则为Δτ′∈(2.071 2 μs,2.977 5 μs)。

四种模式的问答信号特征匹配规则如表6所示。

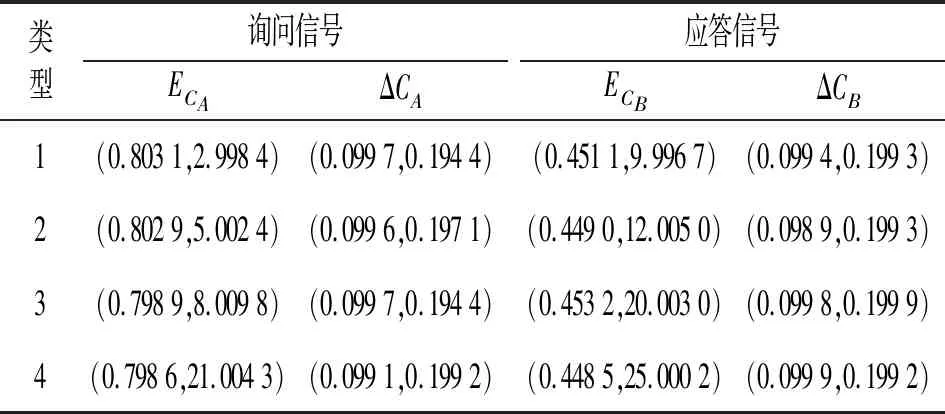
表6 信号特征配对规则

对比场景1和场景2挖掘出的信号时间配对和信号特征配对规则可看出，不同场景下提取规则近似。

用测试样本集对挖掘出的规则进行测试(测试10次平均值，测试次数对测试结果影响较小)，置信度阈值根据式(9)设置为30%，场景1平均配对正确率99.2%，虚警率0，规则的置信度95%；场景2平均配对正确率99.2%，虚警率0.1%，规则置信度为92%；规则置信度大于阈值，即规则可信。

3.2 基于实侦数据集的算法验证

为验证本算法的实用性和鲁棒性，从某实采询问数据中读取时长10 s数据为询问训练样本(4 111个)，读取对应时长的应答数据作为应答训练样本(61 032个)。在实采训练样本基础上共构建42 404个2-项候选集，聚类结果如图9所示，共形成16种类别，每种类别的项集数量和支持度如表7所示。

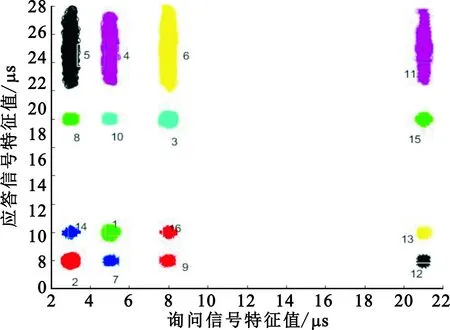
图9 信号对聚类结果(实采数据)

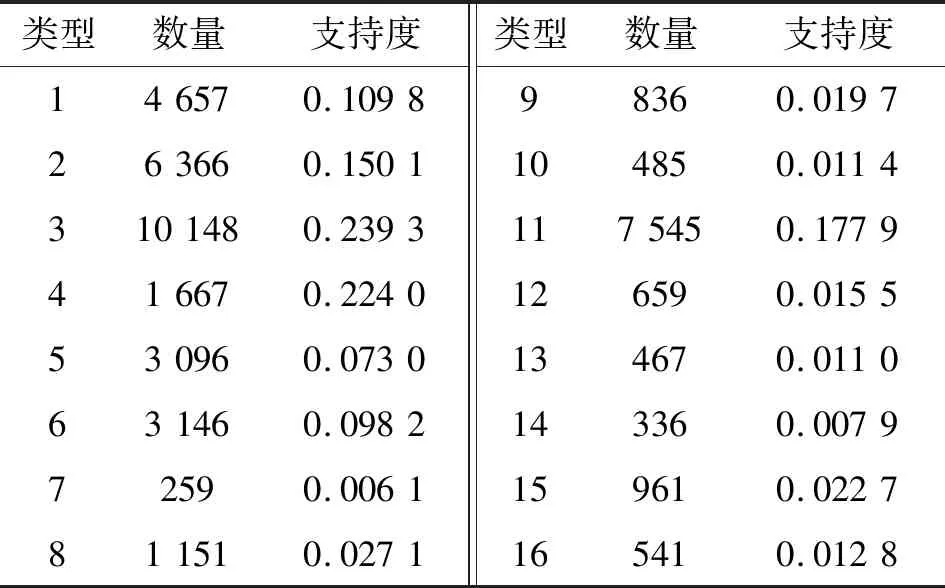
表7 类型支持度(实采数据)

支持度大于0.1的类别共四种(类型1、2、3、11)，每类对应时间差如表8所示，与仿真数值相似。

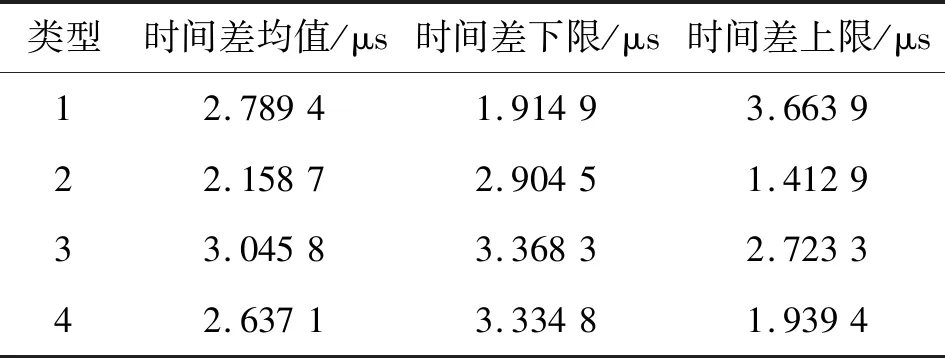
表8 问答时间差(实采数据)

截取另外1 s时长询问数据及对应时长的应答数据作为测试样本对规则进行测试，平均置信度达到77.43%，大于置信度阈值30%。四种高支持度的模式特征也与IFF的信号模式1/2/3/C特征符合。

从实采数据处理结果可看出，实侦条件下信号密集度较高，非匹配模式间错误匹配的概率较高，但正确的匹配项集仍具有较高的支持度。根据经验，针对上述情况可采用已知的局部先验知识对配对进行进一步筛选；对完全未知信号，则可通过长期积累数据进行持续验证和筛选。

3.3 算法性能影响因素分析

3.3.1 时间窗TW对算法性能的影响

时间窗TW对配对置信度、正确率及虚警率的影响如图10所示。

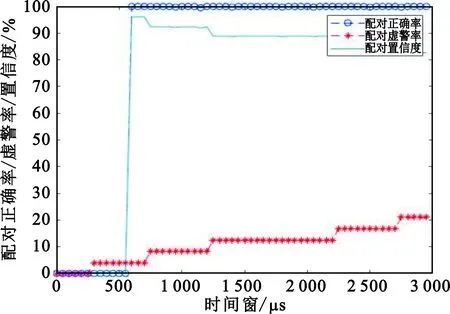
图10 时间窗对算法性能影响

3.3.2 信号参数测量误差对算法性能的影响

在TW值一定的情况下，信号脉宽、脉冲间隔、到达时间等主要参数的测量误差将影响配对性能。

参数测量误差对信号对聚类的影响如图11所示，其中(a)和(b)为误差均值均为0.2 μs条件下聚类结果降维视图，(c)和(d)则为误差均值分别为0.2 μs、0.5 μs、2 μs条件下聚类结果的降维可视化图。可看出，随着误差增大，类内距离增大、类间距离减小；在类相似度较高时，参数测量误差对聚类效果影响增大。

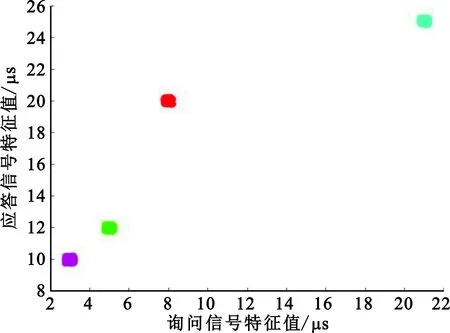
(a)误差均值0.2 μs时聚类结果(脉冲间隔维度视图)

在不同误差条件下测试误差偏差变化情况。设置脉宽误差均值变化范围为0.025～0.25 μs，步进0.025 μs；到达时间、脉冲间隔误差均值变化为0.1～1 μs，步进0.1 μs。10种条件下的仿真结果如图12所示，可见参数测量误差增大造成规则偏差范围增大。

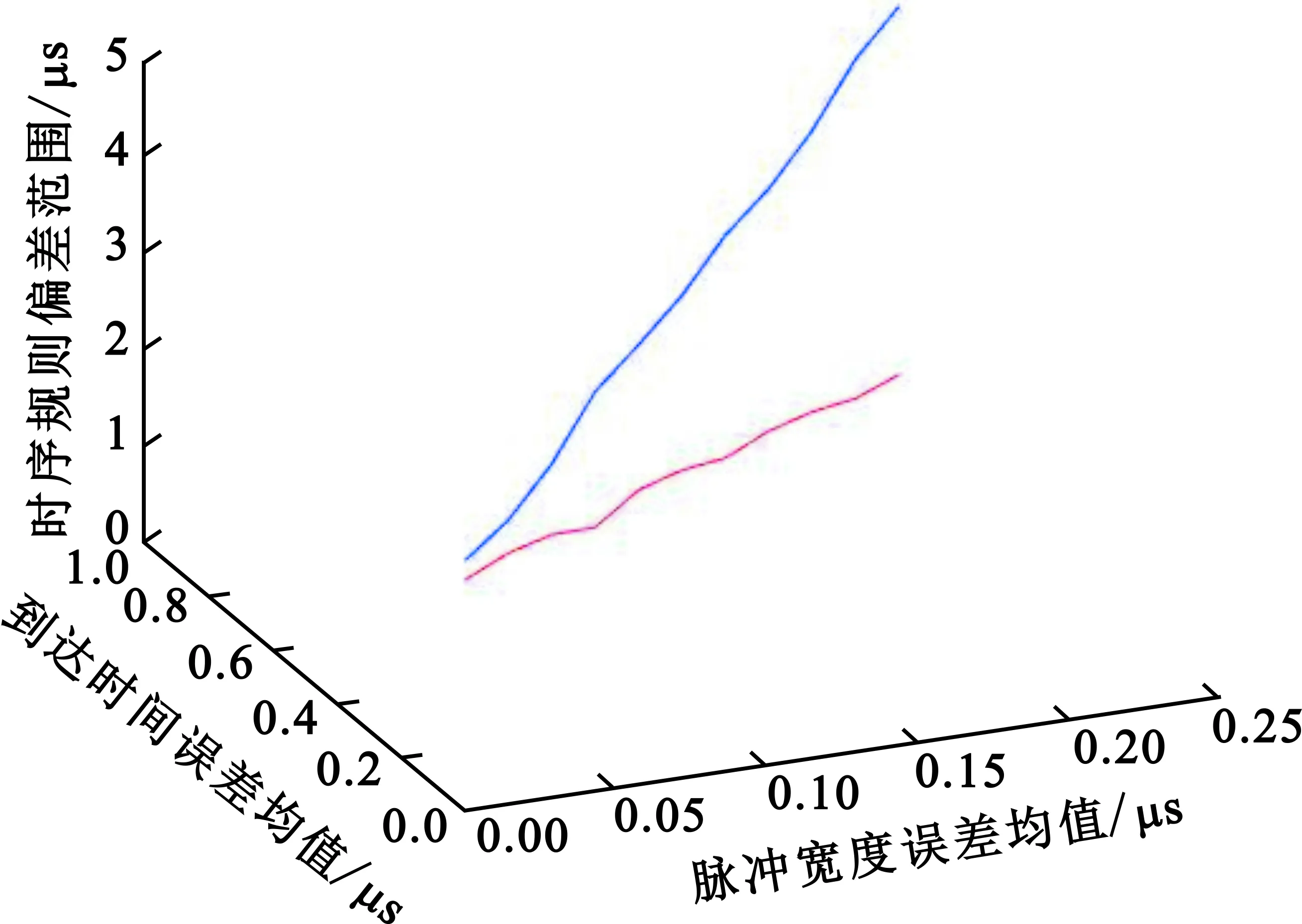
(a)到达时间、脉宽误差均值对时序规则偏差的影响

规则偏差范围增大对配对置信度、正确率及虚警率造成一定影响。设规则偏差率为规则偏差值与真实规则的比例，利用上述10种误差条件下挖掘的规则进行配对测试，仿真测试结果如图13所示(每种规则测试10次取平均)，可见随着参数测量误差增大，规则偏差范围增大，规则偏差率增大，配对正确率提高，但虚警率和置信度下降。

由仿真分析可知，时间窗和参数测量误差对算法性能存在一定的影响：时间窗过窄无法配对，随着时间窗加大，配对正确率可达到100%，但虚警率逐渐增大，即将非匹配信号对错误配对；信号参数测量误差(尤其是时域参数测量误差)将影响规则偏差范围，测量误差增大，偏差范围增加，配对正确率提升，但配对置信度与虚警率快速提升。

3.4 与基于内涵解译的配对算法性能对比

文献[6-7]采用信号特征、目标位置、信号模式类型、解码解译结果进行IFF信号和DME信号的配对，对信号先验知识依赖程度较高；本文方法主要采用脉冲宽度、脉冲间隔、到达时间以及信号频率、调制方式等信号时频域特征参数，通过模式挖掘提取规则进行信号配对，无需模式类型和解码解译结果，先验知识依赖程度低。图14是以场景2为背景，不同解码准确率条件下的算法对比结果。本文算法对编码识别正确率无依赖，解码正取率低于95%时可取得较高的信号配对正确率。

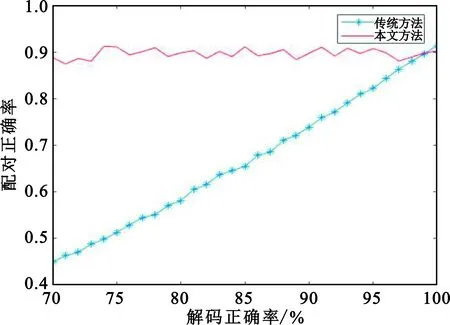
图14 性能对比情况

3.5 算法复杂度仿真分析

设询问信号数据量从1 000到100 000，应答信号数量为询问数量的5倍(按实采经验设置)，图15为不同数据量和节点数量条件下按式(12)估算的算法复杂度仿真结果。从图中可看出，算法复杂度随着数据量增大而增加，采用分治策略将数据分片后增加速度随着询问节点数增大而减缓。

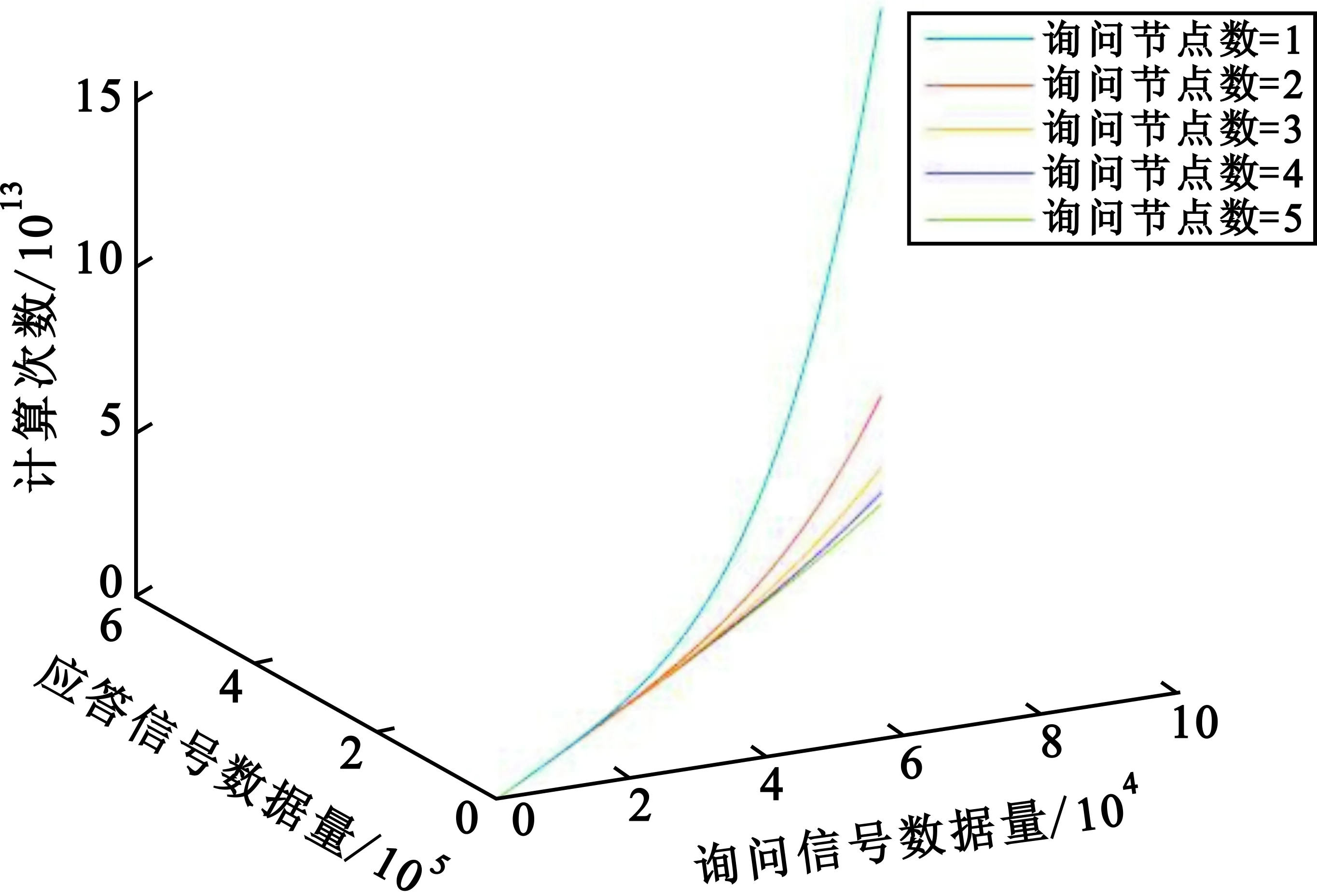
图15 算法复杂度仿真

4 结束语

本文以IFF系统为研究对象，针对协议未知或部分已知的情况，提出一种基于时序频繁模式挖掘的问答配对规则提取方法。利用系统问答信号特征模式和时序先后关系，基于问答时间序列数据构建询问-应答2-项候选项集，通过候选项集聚类分析挖掘频繁项集，提取信号配对规则，进而实现问答信号的准确配对。仿真和实采数据验证结果表明，该方法能在缺乏先验知识的情况下提取问答信号配对规则进而实现信号配对，为信号通联分析提供有力支撑，具有较好的实用价值。

本文的下一步工作是研究复杂环境下信号通联规则挖掘的方法和算法在大数据平台的实现方法，以适应真实复杂战场环境下获取的海量信号数据，提升算法的工程实用性。