大规模MIMO相关信道下的联合天线分组和天线选择*
冀笑伟,李 莉,魏 爽,张 铭
(上海师范大学 信息与机电工程学院,上海 201418)
0 引 言
随着信息技术高速发展,大规模多输入多输出(Massive Multiple-Input Multiple-Output,Massive-MIMO)技术成为第五代通信网络中的关键技术之一,具有超大规模天线阵列的MIMO系统能够有效提高系统的吞吐量[1]。然而,在实际通信系统中,基站端大量天线会导致系统功耗增加,而天线选择技术通过选择部分有效天线进行信息传输,可降低Massive-MIMO系统的硬件成本及系统功耗[2]。
要找到最大信道容量或最小误码率的最优天线子集需要穷尽搜索,其计算复杂度将随可用天线数的增加呈指数增长,许多文献致力于寻找低复杂度且信道容量最大化的天线选择方法。文献[3]提出了一种改进的二进制粒子群天线选择算法,为实现信道容量最大化,将天线选择问题转化为选择合适的二进制编码串问题,有效降低了计算复杂度。文献[4]研究了接收端的天线选择问题,采用基于最优分支定界(Branch-And-Bound,BAB)的方法来寻找最优天线子集,以使信道容量最大化。结果表明,基于BAB搜索的天线选择方法比基于累加搜索方法更有效,在天线数量较大的情况下可以实现3个数量级的加速。文献[5]提出了一种迭代交换天线选择方法,实现了目标天线的“局部”交换,其算法复杂度很低。
目前,多数天线选择算法都假设信道是理想独立状态。然而,大规模MIMO系统中密集的天线部署会导致天线之间具有强相关性,实际通信系统中信道往往是相关的。因此,具有空间相关性信道场景下的天线选择技术值得研究[6-9]。对于强相关信道场景中的天线选择技术而言,由于天线相关性过高会弱化大规模天线技术的增益效果,因此,在进行天线选择之前,若根据某些准则将天线进行分组,然后从不同组内选择有效发射天线,就可以减少强天线相关性对系统性能造成的影响[10-15]。文献[11]提出了联合天线分组和天线选择的低复杂度贪婪算法,可以减少系统的理想信道状态信息(Channel State Information,CSI)反馈开销,但同时也增加了组间干扰,在高信噪比的情况下会导致性能饱和。文献[13]提出了一种分组辅助广义空间调制方案,将发射天线分成若干组,通过将相邻天线组成一组形成块分组,或通过最大化一组天线间的距离,产生交织分组,但其中的两种分组方法都是基于统计信道信息,在有瞬时信道相关知识的情况下可以进行改进。文献[14]研究了基于最大比传输预编码天线分组的系统能效问题,将文献[13]按照相邻原则进行天线分组的思想应用到天线选择技术中,有效抑制了天线相关性对系统性能造成的影响。然而,由于天线相关性同时受天线间距、天线分布图、信号波达角、角度扩展等因素的影响,故粗略地根据相邻原则分组并不一定能保证组内天线相关性最强。文献[15]提出了一种天线分组空间调制方案,利用瞬时信道相关矩阵将发射天线分成多组,通过将强相关天线分到同一组以支持空间调制,而将弱相关天线分组以获得多路复用增益,从而减轻了天线相关性的影响。
目前,天线分组技术多用于空间调制方案中,而对于相关信道下的天线选择方案而言,若在天线选择之前先将天线分为若干组,再在不同组内选择有效发射天线,就可以在避免天线强相关性抑制天线选择增益效果的同时减少天线搜索范围。现有文献中,针对相关信道下基于天线分组的天线选择算法研究尚且不足,故本文借鉴文献[15]根据瞬时信道相关矩阵进行天线分组的思想,研究Massive-MIMO系统中的天线选择问题,针对系统下行链路场景,建立发射端天线具有空间相关性的大规模MIMO系统模型,提出相关信道下联合天线分组和天线选择算法,并与基于相邻天线分组的天线选择算法对比,分析所提算法的系统遍历和速率性能表现。仿真结果表明,在发射端天线相关性较强的情况下,本文所提算法相较于对比算法在遍历和速率方面具有较强的优越性。
1 多用户Massive-MIMO系统模型
考虑多用户Massive-MIMO系统下行链路场景,假设系统在时分双工模式下运行,且收发端已知信道状态信息。基站端配备N根发送天线,接收端有K个单天线用户,且N>>K,如图1所示。
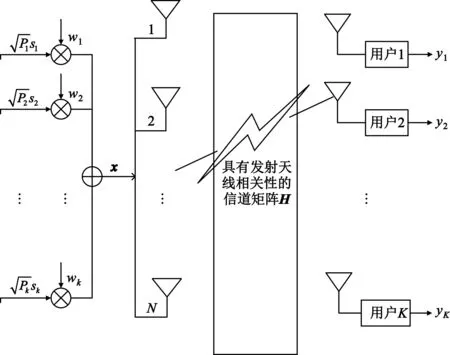
图1 多用户大规模MIMO系统下行链路模型
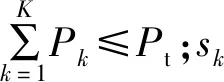
为表征Massive-MIMO系统发射端天线之间的相关性,且方便后续仿真验证时定量描述发射天线间相关性大小,利用Kronecker信道模型对信道矩阵进行建模[16],具体表示为独立同分布瑞利衰落信道与发射端天线相关矩阵的乘积:
H=HwRt1/2。
(1)
式中:Hw∈K×N表示独立同分布瑞利衰落信道,Rt∈N×N表示发射端天线的相关矩阵。Rt采用指数相关模型形成:
(2)
式中:Rt中元素满足(Rt)i,j=μ|i-j|,μ表示发射端天线的相关因子,0≤μ≤1。
式(1)中H是发射天线与接收天线之间的信道矩阵,其大小为K行N列。设矩阵H的第(i,j)个元素hi,j是从第j根发射天线到第i根接收天线的路径增益,为清晰直观地表示矩阵各元素的物理意义,现将式(1)中H具体为
(3)
为方便后续表示用户k的接收信号,将信道矩阵记为H=[h1T,h2T,…,hKT]T∈K×N,其中hk=[hk,1,hk,2,…,hk,N]∈1×N表示用户k的接收天线与发射天线间的信道向量。
已知用户的接收信号为有效信号、其他用户干扰及噪声干扰之和,则用户k的接收信号yk可表示为
(4)
式中:nk是用户k处的加性高斯白噪声,其均值为0,方差为σk2。
根据式(4)可知,用户k的信干噪比(Signal-to-Interference plus Noise Ratio,SINR)可表示为
(5)
因此,用户k的瞬时信息速率Rk表示为
Rk=lb(1+SINRk)。
(6)
此时,多用户大规模MIMO系统的下行遍历和速率Rsum为
(7)
式中:符号E[·]表示统计平均运算。
对于图1所示的Massive-MIMO系统下行链路模型,基站端天线之间的强相关性会导致系统和速率下降,如果首先对大规模天线阵列进行分组,然后在各组内选择合适的天线发送信号,就可以避免选中分布密集的天线进行信号传输,从而改善系统的性能。然而,文献[13]中仅粗略地根据相邻原则进行天线分组并不一定能保证组内天线相关性最强,但是天线分组的目的就是将相关性较强的天线分为一组,针对上述问题,本文考虑利用瞬时信道相关矩阵对天线进行分组,提出相关信道下联合天线分组和天线选择算法。
2 联合天线分组和天线选择算法
在图1所示的Massive-MIMO系统中,基站端大规模天线阵列中天线间隔很小,发射天线之间具有很强的相关性,本文根据瞬时信道相关矩阵对天线进行分组,提出一种基于瞬时信道相关矩阵的分组策略。首先,根据式(3)所示的信道矩阵H,求出瞬时信道相关矩阵,记为M[15]:
(8)
(9)
式中:符号‖·‖表示求范数运算,符号[X]i,j表示矩阵X的第(i,j)个元素,Mi,j表示第i根发射天线与第j根发射天线之间的相关系数,Mi,j*表示Mi,j的复共轭运算。式(8)中,若|Mi,j|较大,则说明第i根发射天线与第j根发射天线在同一时刻的相关性较大。
其次,将N根发射天线平均划分为L(L≥K)组,组内天线数Ng=⎣N/L」,符号⎣·」表示向下取整运算。分组时从先N根天线中选出Ng根构成一组,再从剩余(N-Ng)根天线中选出Ng根构成另一组,以此类推,共分出L组天线,剩余NmodL根天线暂不做处理,符号mod表示求余运算。将N根发射天线分成L组的组合总数D[15]为
(10)
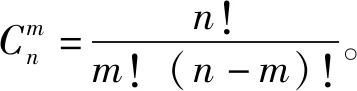
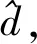
首先,输入N、K、H、L、Ng参数,分别根据式(8)和式(10)计算瞬时信道相关矩阵M和候选组合总数D。
其次,对于1≤d≤D的每个组合,计算
(11)
式中:Mi,j(l)表示来自第l组的第i根发射天线与第j根发射天线之间的相关系数。
(12)
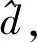
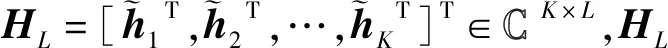
(13)
相应地,天线选择完成后,系统下行遍历和速率Rsum′具体为
(14)
上述相关信道下联合天线分组和天线选择算法的具体实现流程如图2所示。
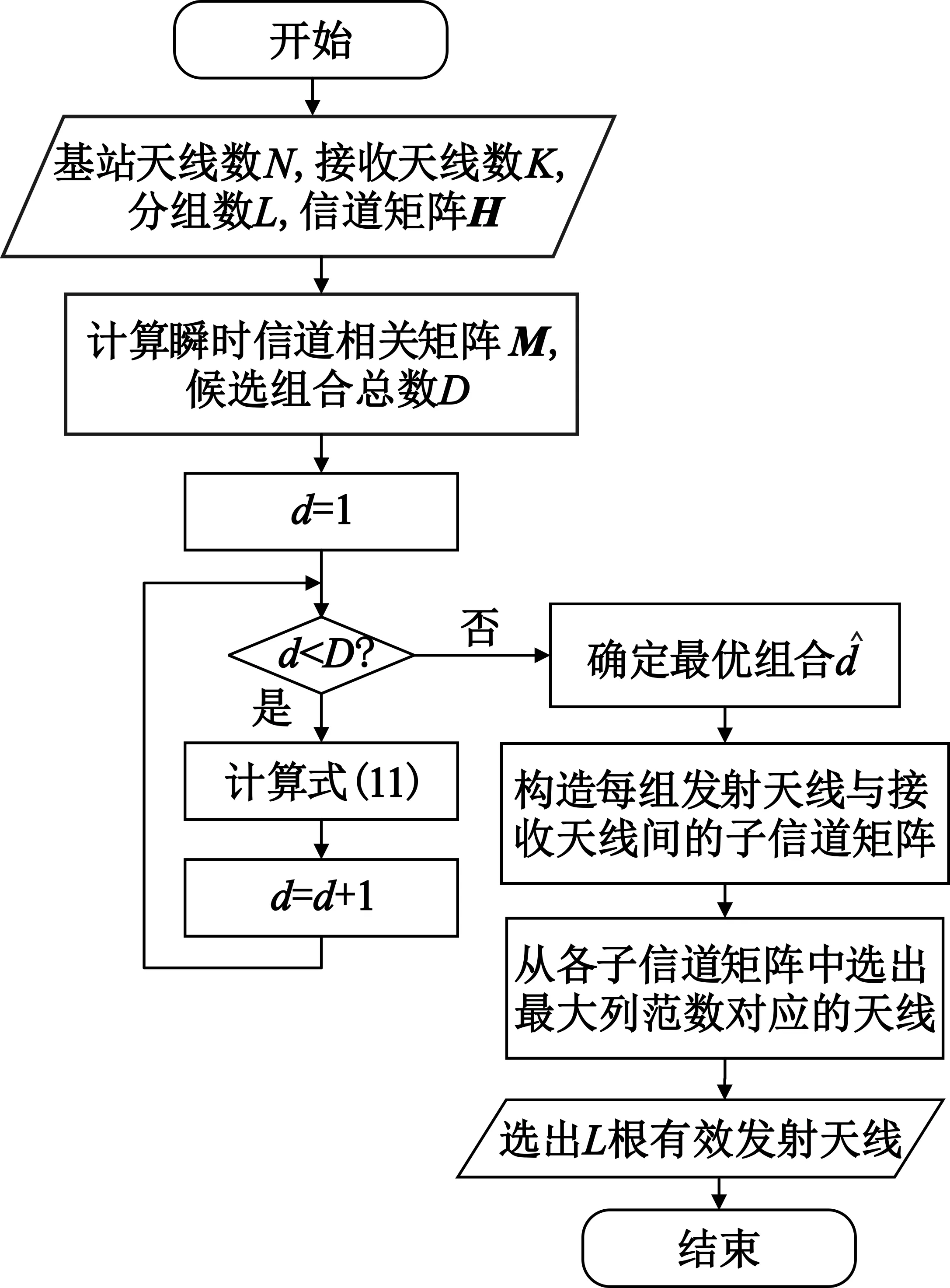
图2 联合天线分组和天线选择算法流程图
3 仿真结果与复杂度分析
3.1 仿真结果
为验证本文所提算法的有效性,针对系统和速率性能进行仿真,并与最优天线选择、基于相邻天线分组的天线选择以及基于信道矩阵列范数的天线选择算法作对比。其中,最优天线选择通过穷尽计算所有可能天线子集的信息和速率,选择出使信息和速率性能最佳的天线子集;基于相邻天线分组的天线选择首先将天线按照相邻原则均分为若干组,再在每组中选择合适的天线作为有效发射天线;基于信道矩阵列范数的天线选择是从信道矩阵中选出具有最大Frobenius范数的L列,对应的列序号即为所选天线的序号,最终选出L根天线构成所选天线子集。仿真中,假设接收端各个天线总接收功率等于基站总发送功率,且每根接收天线采取等功率分配策略,利用迫零预编码技术[17]预处理发送信号,信道采用式(1)中描述的相关模型,基站天线总数N=32,单天线用户数K=2,分组数L=2。
图3分别描述了信道状态良好时(μ=0.2)和信道状态较差时(μ=0.9)不同天线选择算法下系统遍历和速率随信噪比的变化。
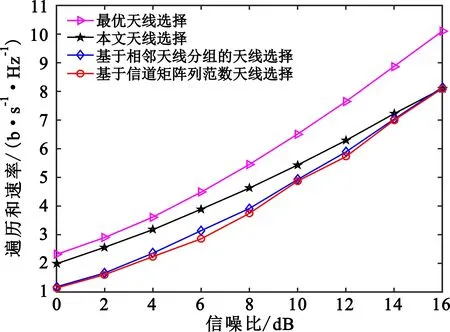
(a)N=32,K=2,L=2,μ=0.2
图3(a)中,在信道状态良好(μ=0.2)的情况下,当信噪比为10 dB时,本文天线选择算法系统和速率比基于相邻天线分组的天线选择算法提高了约10.2%。图3(b)中,在信道状态较差(μ=0.9)的情况下,当信噪比为10 dB时,本文天线选择算法和速率比基于相邻天线分组的天线选择算法提高了约27.5%。
对比图3(a)和图3(b)可知,随着信道状态变差,遍历和速率也有所下降,两种情况下本文所提算法均与最优天线选择算法性能接近,本文算法若要与最优天线选择算法达到相同的和速率,仅需将其信噪比提升1~2 dB即可。例如,当μ=0.9时,若系统实现5 b/s·Hz-1的和速率,最优算法和本文算法分别需要的信噪比为8 dB和10 dB左右。另外,所提算法性能优于基于信道矩阵列范数的天线选择算法,这是因为对天线进行分组后再进行天线选择可避免选中分布密集的天线发送信号,有效克服了天线间相关性的影响。
由上述分析可知,在天线相关因子较大(μ=0.9)时,本文所提算法相较于基于相邻天线分组的算法具有更强的和速率优势。这是因为当发射天线相关性较强时,所提算法可以保证组内天线相关性尽可能的高,而不同组的发射天线相关性尽可能低,由此减轻了天线选择时因选中强相关性的天线而造成的性能损失,从而提高了大规模MIMO系统的和速率。这也印证了强相关信道条件下本文天线分组策略的优越性。
图4描述了当K=2、L=2、SNR=10 dB、μ=0.9时,和速率随发射天线数的变化。由图可知,随着发射天线数目增加,系统和速率性能总体呈上升趋势。本文算法和速率与最优算法有一定差距,但是优于基于相邻天线分组的天线选择算法,并明显优于基于范数的天线选择算法。当发射天线数N=32时,本文算法的和速率比基于相邻天线分组的算法约提高了19.6%。
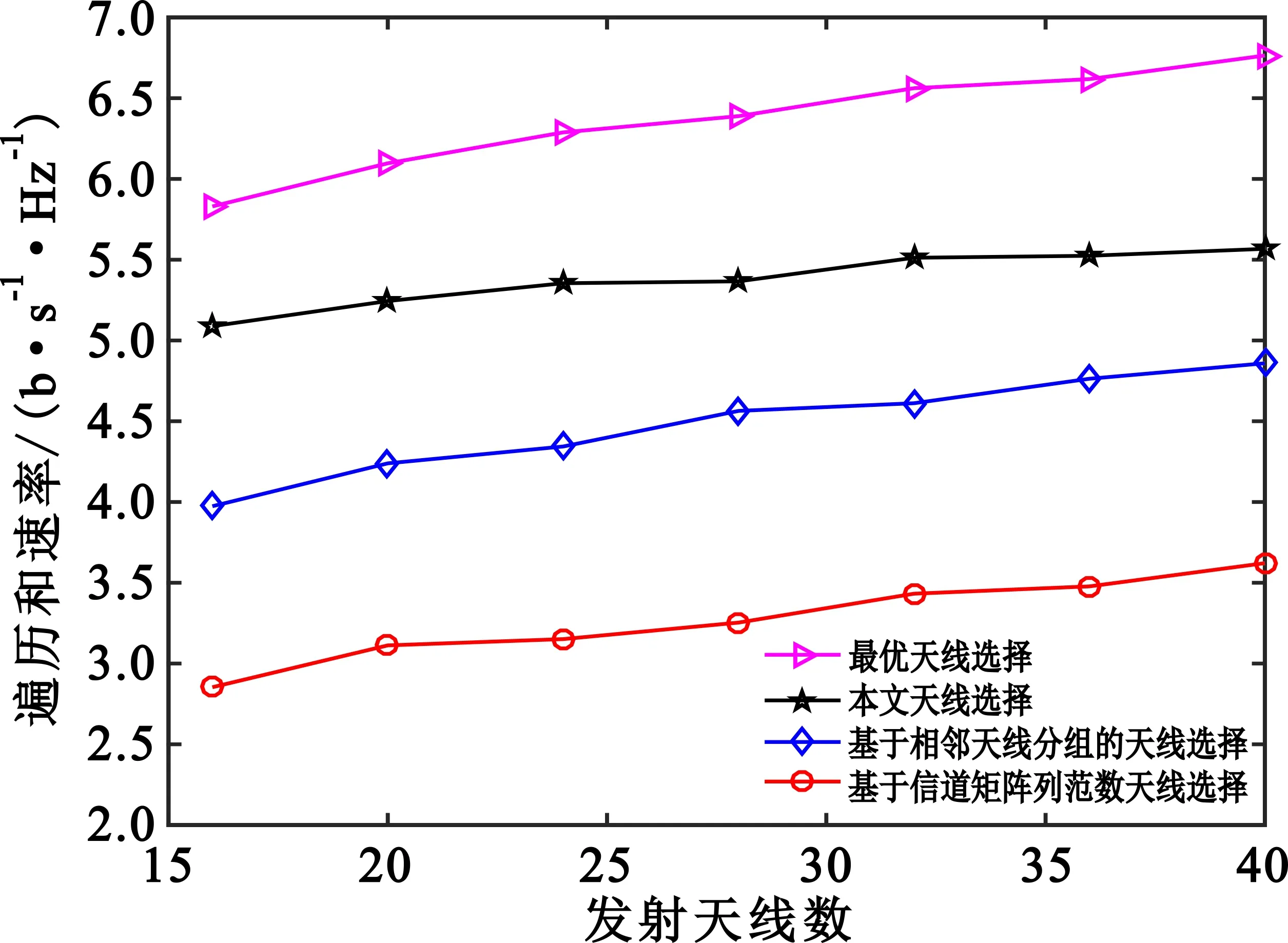
图4 和速率随发射天线数的变化(K=2,L=2,SNR=10 dB,μ=0.9)
图5描述了当N=32、K=2、L=2、μ=0.9时,不同天线选择算法分别在独立瑞利衰落信道模型和空间相关信道模型下的和速率性能。由图可知,两种天线选择算法的和速率在相关信道模型中都稍逊色于在独立信道模型中的表现,这就印证了前文提到的相关信道场景下强天线相关性会抑制天线选择增益效果的结论。另外,即便在独立信道条件下,本文算法相较于对比算法也拥有更好的性能,当SNR=8 dB时,本文算法的和速率比基于相邻天线分组的算法约提高了57.8%,表明了本文算法在不同信道场景中的良好适应性。
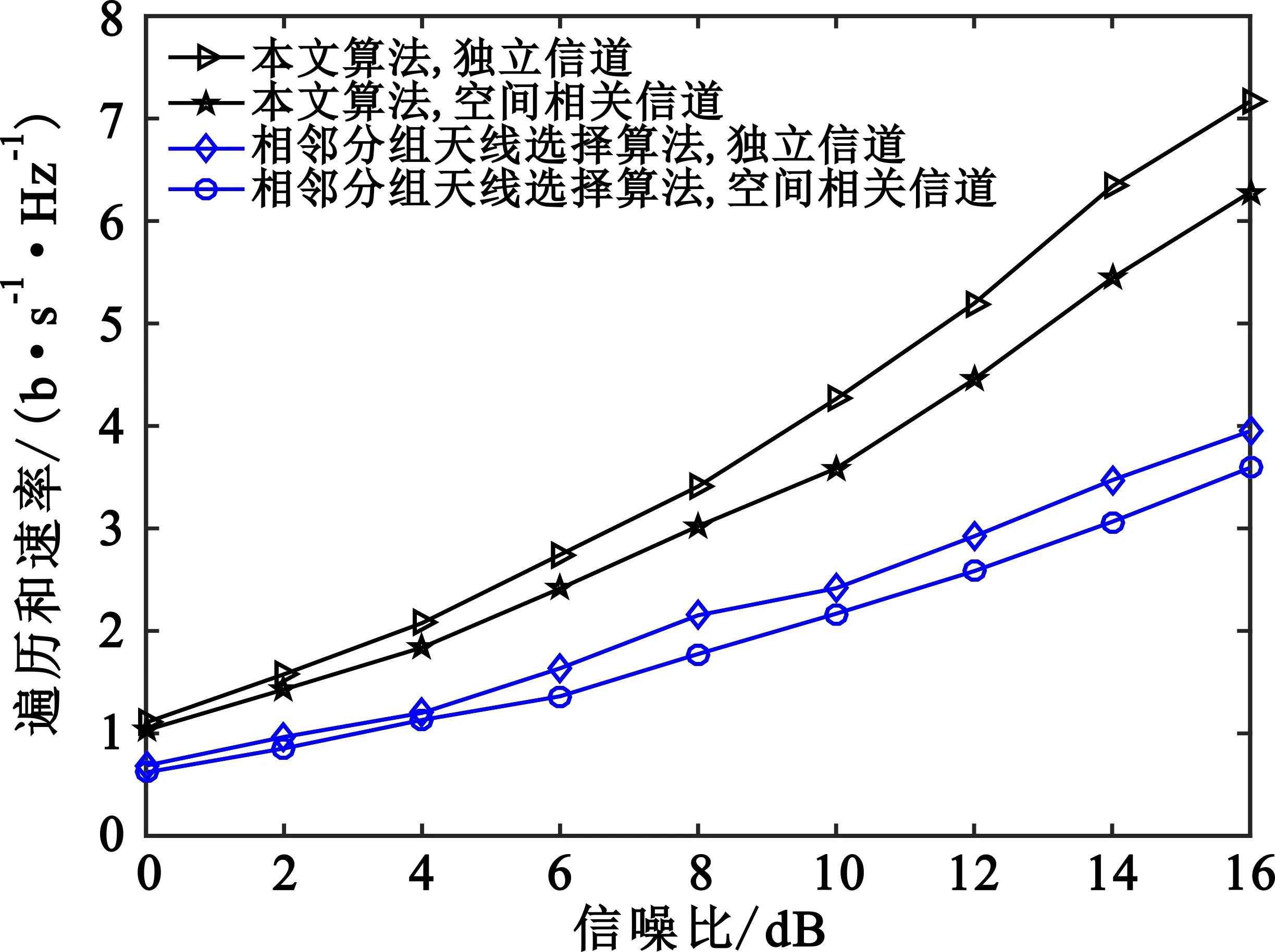
图5 不同信道模型下和速率随信噪比的变化(N=32,K=2,L=2,μ=0.9)
3.2 复杂度分析
本文算法复杂度以天线选择过程中运算乘法的次数为衡量标准。现将不同天线选择算法复杂度以及利用不同天线选择算法求和速率时仿真运行时间(N=16,K=L=2)进行对比,具体结果如表1所示,其中N、K、L分别为发射天线数、单天线用户数、分组数。
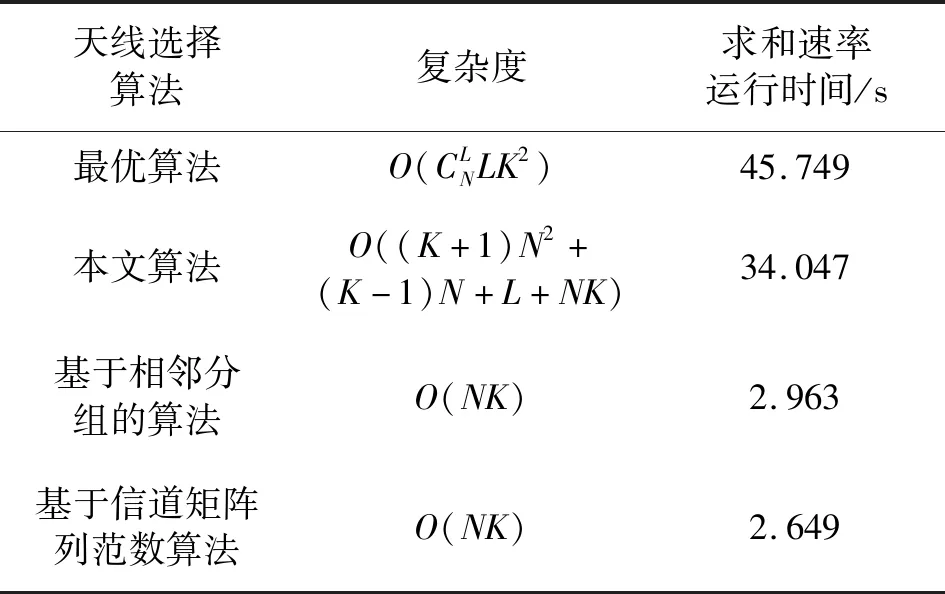
表1 各算法复杂度比较
对比表1中利用各算法求和速率时运行时间可知,最优算法运算时间最长,本文所提算法的运行时间比最优算法降低了约25.6%;由于本文算法分组过程中需要遍历计算各个可能分组组合的Jd值,故其运行时间高于基于相邻天线分组的算法和基于范数的天线选择算法,这是所提算法获得相对优越和速率性能所付出的代价;基于相邻分组的算法和基于信道矩阵列范数的算法天线选择过程中乘法运算次数相同,故利用上述两者算法计算系统和速率时仿真运行时间也相差无几。
4 结束语
本文针对大规模MIMO密集部署天线造成发射天线间相关性很强,从而影响信号传输,进而导致系统性能降低的问题,提出了基于瞬时信道相关矩阵的天线分组方案,将相关性较强的天线分到同一组内,不同组内的天线相关性相对较弱,然后从由组内发射天线和接收天线构成的各个子信道矩阵中基于信道矩阵列范数准则选择有效发射天线。这种基于天线分组的天线选择算法可有效降低天线间强相关性对系统性能的影响。仿真结果表明,本文所提算法在遍历和速率性能方面优于基于相邻天线分组和基于信道矩阵列范数的天线选择算法。另外,本文算法若要与最优天线选择算法达到相同的和速率,仅需将其信噪比提升1~2 dB即可。然而,分组算法中天线组合总数会随分组数的增加而增加,这将导致算法复杂度提升。在接下来的研究中,需要考虑降低复杂度的分组算法,并将本文所提天线选择算法与适用于相关信道的预编码方案相结合,以进一步提升系统性能。

