一种新架构的数字预失真系统及其实现*

张红升，易胜宏，孟 金，卫中阳，马小东

(重庆邮电大学 a.光电工程学院;b.微电子工程重点实验室,重庆 400065)

0 引 言

数字预失真(Digital Pre-distortion,DPD)法由于其可配置性和低成本性，已经被广泛应用在通信射频前端上[1]。数字预失真的原理是，基带信号在经过数模转换器(Digital-to-Analog Converter,DAC)和功率放大器之前，预先经过一个具有和功放拟合度较高的模型电路，该模型具有和功放互逆的输入-输出特性，通过补偿增益、调整功放模型参数，达到预失真系统输出线性化的目的。经过数字预失真处理后的基带信号在通过DAC和上变频后，通过射频接口和功率放大器发射出去，使得其上变频信号具有较低的邻信道功率比(Adjacent Channel Power Ratio,ACPR)，即邻频率信道(或偏移量)的平均功率和发射频率信道的平均功率之比。对于宽带码分多址(Code Division Mulitiole Access，WCDMA)发射系统，定义主信道的上下保护边带宽度均为5 MHz，系统输出信号的ACPR的值应小于-45 dBc[2]。

但是，目前的数字预失真系统存在着集成度不高、软核处理能力较差、预失真架构过于复杂等缺点。针对这些缺点，本文提出了一种基于Zynq和AD9361的高性能预失真系统。该系统基于Zynq的Cortex A9双核，使得系统的性能较目前常用的Microblaze软核提高了3倍以上。系统的功放数字模型采用的是记忆多项式模型，并且提出了新的查找表+卷积结构，免去了原有查找表模块的大规模数据交换操作，降低了系统的复杂度。自适应算法采用归一化最小均方(Normalized Least Mean Square,NLMS)算法，该算法具有比最小均方(Least Mean Square,LMS)算法更快的收敛速度和更小的稳态误差。实验证明，新提出的预失真结构具有更短的运算周期、更低的硬件资源消耗和更简单的硬件结构，且经预失真处理后的邻信道功率比降低了10 dB，满足系统的传输需求。

1 基于记忆多项式模型的硬件实现方法

1.1 各类预失真器结构比较与分析

工程中常用的功放数字模型包括Volterra级数、记忆多项式模型(Memory Polynomial,MP)、广义记忆多项式模型(General Memory Polynomial,GMP)等，其中，Volterra级数是对功放拟合度最高的模型，但是由于其模型系数过多，提取困难，故仅在仿真中采用此模型；GMP模型为Volterra级数的简化版，同样具有较多的模型系数，并且加入了延迟项和超前项，具有较高的复杂度；而MP模型只提取了Volterra级数的对角项，模型系数大大减小，非常适用于工程实现[3]。记忆多项式的数学模型如下所示：

(1)

式中：K为非线性阶数，Q为记忆深度。目前工程实现中，针对MP模型硬件实现使用得最多的方法包括多项式法和查找表法，其中多项式法是根据MP模型的数学公式直接搭建其硬件逻辑。以非线性阶数K=2、记忆深度Q=2为例，其多项式法的硬件实现框图如图1所示。

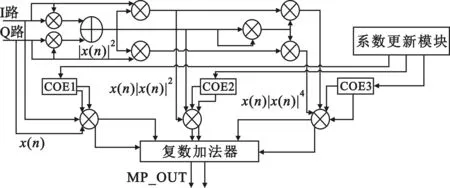
图1 多项式法硬件实现

可以看出，在上述条件下，此方法所消耗的硬件乘法器较多，其中，实数乘法器为7个，复数乘法器为3个。由于FPGA内部的硬件乘法器逻辑资源较为宝贵，故在工程实现中常常采用查找表(Lookup Table,LUT)法[4]，其硬件实现框图如图2所示。

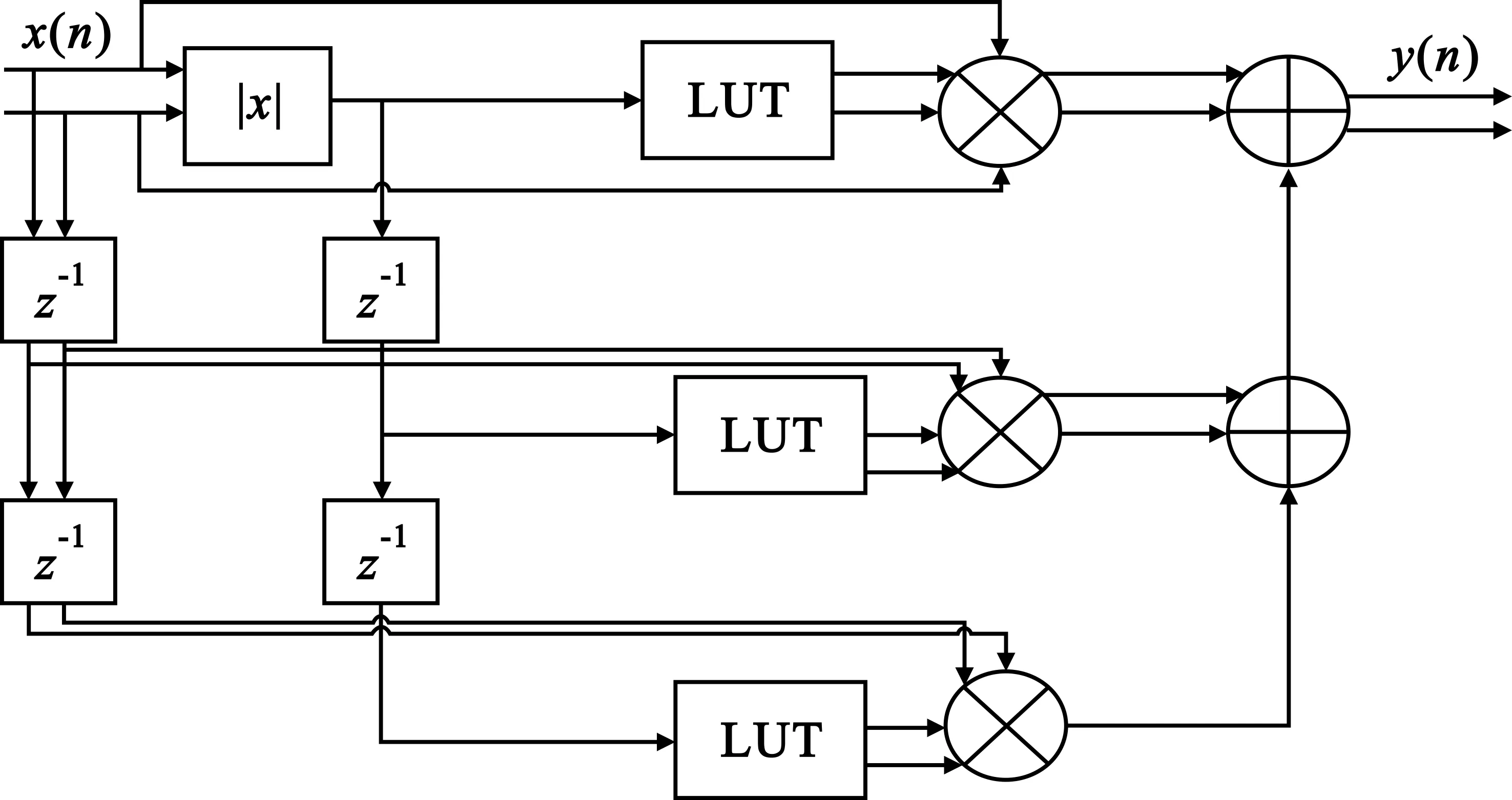
图2 查找表法硬件实现

查找表的项数由输入信号幅度的量化位宽而决定，若量化位宽为N，则查找表项数为2N个。查找表的原理如下:

以MP模型为例，由式(1)的结构可以看出，其前半部分可以单独看成一个关于|x(n)|的函数，即

(2)

则记忆多项式的表达式可以重写为

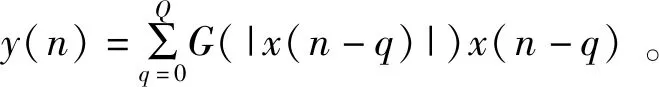
(3)

故G(|x(n)|)可以看作一个函数，|x(n)|为其索引。由于FPGA内部包含了丰富的RAM资源，故查找表法更适用于硬件平台上[5]。此方法消耗了3个复数乘法器和3块RAM，相对于多项式法减少了7个实数乘法器。但是，此模块需要求取信号的幅值|x(n)|，此运算为非线性运算，需要利用Cordic核来求取输入信号的幅度，故会消耗较多的逻辑资源，并且由于查找表内的数据需要实时更新，对于包含自适应算法的预失真系统，每次预失真模块复增益系数akq的迭代替换都会产生巨大的数据流。在工程实践中，一般采用乒乓操作的方式[6]，将上下行查找表的深度均设置为2的次方数，在读取上部分RAM的同时，将更新的复增益值写入下部分RAM，以保证数据迭代替换不出错。较深的RAM会使得数据的更新速度变慢，导致系统整体工作频率降低。

1.2 基于查找表和卷积模块的记忆多项式模块

针对以上两种记忆多项式硬件实现方法的弊端，本文提出了一种基于LUT和卷积算法的新型硬件实现方法。

以非线性阶数K=2、记忆深度Q=2为例，将式(2)拆成

y(n)=a10x(n)+a30x(n)|x(n)|2+a50x(n)|x(n)|4+

a11x(n-1)+a31x(n-1)|x(n-1)|2+

a51x(n-1)|x(n-1)|4+a12x(n-2)+

a32x(n-2)|x(n-2)|2+

a52x(n-2)|x(n-2)|4。

(4)

经过分析可得，式(4)可以分解成以下两个式子：

(5)

(6)

可以看出，式(6)是一个标准的卷积和形式，其中Lk(n-q)为查找表输出L(n)的卷积项，a(2k+1)q为记忆多项式模型的参数，K为非线性阶数，Q为记忆深度。式(5)基于一个查找表架构实现，以输入的x(n)信号为检索地址，即I、Q信号检索输出L(n)，分别为x(n)|x(n)|2,x(n)|x(n)|4,…,x(n)|x(n)|2K一共K个复信号输出，所以查找表模块一共需要K个双端口ROM，而根据输出信号的数学特性可知，L(n)的实部和虚部输出是根据行列对称的，故可以通过更简单的方式检索查找表的输出。本文将经过归一化的输入信号经过5 b量化，查找表的行列数均为32，故ROM深度为1 024。

对查找表内容的检索只需要简单的移位逻辑和加法逻辑即可实现。例如，对于行数为5、列数为7的实部数据，即I=5/32，Q=7/32，可以将列数左移5位并加上行数即可得到本数据对应的输出。由于查找表的对称特性，输入信号的虚部则是将行数左移5位并加上列数。这样设计大大简化了检索查找表的复杂度，提高了查找速度。

由于查找表不包含复增益系数akq，故在硬件实现时不需要进行实时的数据替换。这样做既省略了时序控制电路的设计，又节约了硬件逻辑资源。

基于LUT和卷积算法的新型硬件实现方法的原理图如图3所示。其中，本结构所需要迭代更新的模块仅仅包括卷积模块的复增益系数，其总数为(Q+1)(K+1)，故仅需要同数量的寄存器寄存数据即可。通过硬核处理器模块传输过来的系数更新信号控制寄存器的数据流动，在降低系统复杂度的同时提高了预失真器的工作效率。卷积模块可以利用直接型FIR结构，仅采用一个复数乘法器即可实现卷积功能，大大减少了硬件乘法器的消耗。

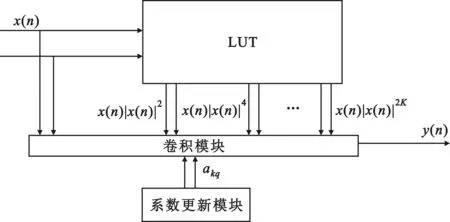
图3 基于LUT和卷积算法的新型硬件实现方法

本文提出的基于LUT和卷积算法的记忆多项式实现模块与其他记忆多项式实现模块的资源消耗对比和基于以上三种预失真器实现方法的预失真系统的运算周期对比如表1所示，其中假定乘法器和加法器的周期都为P，Cordic核的周期为M，功放的延迟为D。

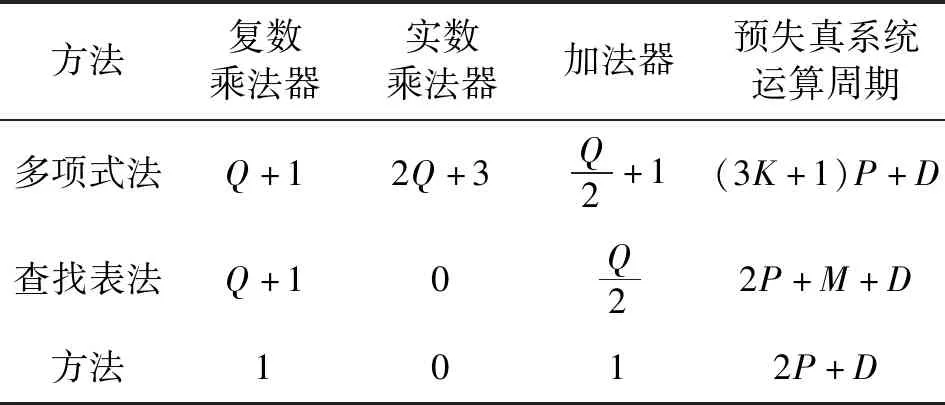
表1 硬件资源消耗及运算周期对比

根据表1，新提出的硬件实现方法的实数乘法器消耗比多项式法减少了2Q+3个，利用直接型FIR实现方法的复数乘法器只消耗了一个，均比多项式法和查找表法少，加法器消耗均比多项式法和查找表法少，且ROM消耗为是根据输入信号的量化位数而定的，具有一定的可控性。对于运算周期，由表1可以看出，新提出的结构比多项式法减少了(3K-1)P个周期，并且比查找表法减少了M个周期，提高了预失真器的工作频率。

2 预失真系统的实现及算法仿真

2.1 预失真结构

本文采用训练预失真的结构，如图4所示。图4中，BBP为基带处理器，用于产生基带数字信号x(n)；w1和w2均为自适应模块更新的预失真器的系数值，该值是通过自适应算法迭代得到的，具体的计算过程根据自适应算法的种类而决定，目前数字预失真技术中常用的自适应算法包括归一化最小均方误差算法、最小均方误差算法和最小均方算法(Least Square,LS)等。

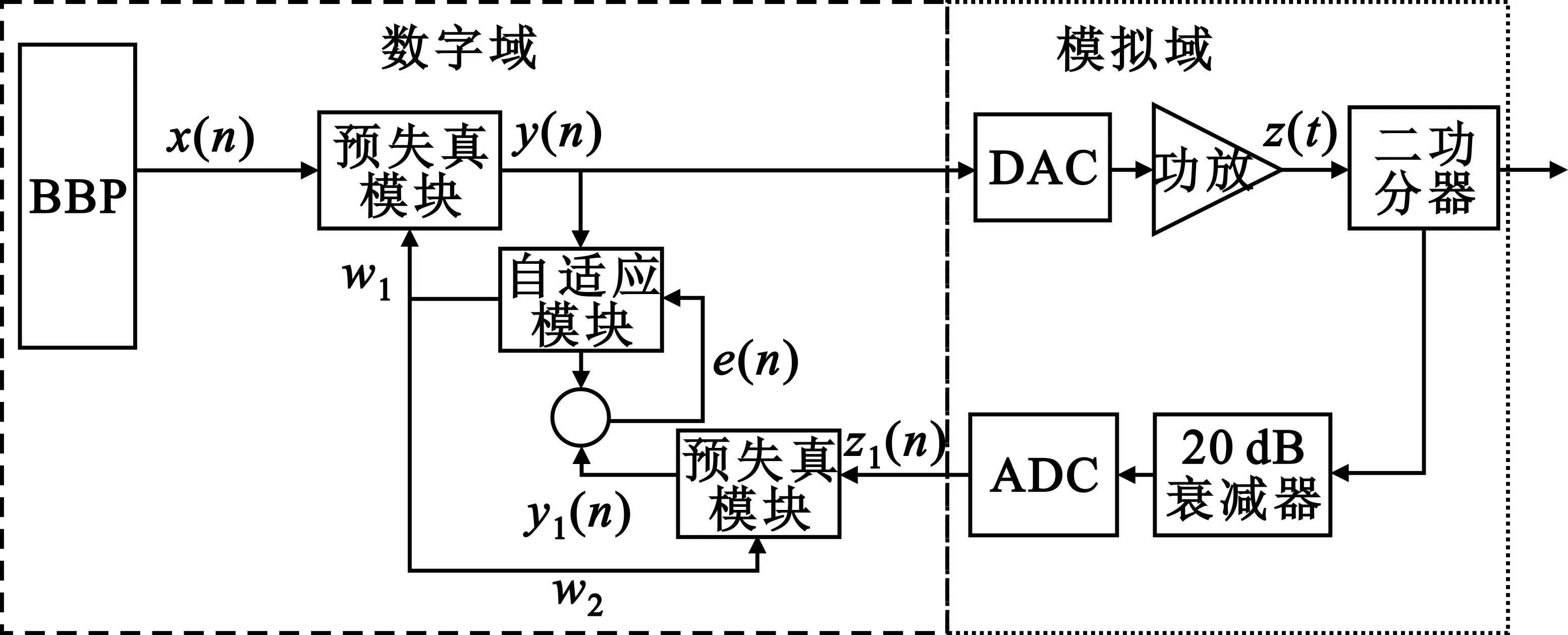
图4 训练预失真系统结构

由于训练预失真模块可以保证系统得到全局最优解，该结构的反馈支路首先对功放输出进行衰减，然后以功放输入和功放模型求逆模型的输出的差值为误差信号，对功放逆模型进行迭代自适应学习，得到功放的逆模型参数，具有稳定、收敛速度快的特点，故本文选择这种结构实现预失真系统。

2.2 自适应算法选择

设预失真模块的通道函数为D(n),故y(n)=D(x(n))。通过功放并返回数字域的信号z1(n)同样通过预失真模块后的输出为y1(n)=D(z1(n))，则误差信号可以表示为

e(n)=D(x(n))-D(z1(n))。

(7)

NLMS算法是基于LMS算法的改进版，对算法的原有步长进行归一化处理，是一种变步长的自适应算法，收敛速度得到了一定的提高。其算法如下所示：

(8)

式中：α为一个定值，w为每次迭代更新的预失真模块参数，x(n)为自适应模块输入信号，y(n)为x(n)经过横向滤波后的信号，d(n)为参考信号(期望信号)。为了使算法收敛，α的值一般设置为如下区间:

0<α<2 。

(9)

接下来，设置LMS算法步长μ为1/32，设置NLMS算法的α为0.2，对两种算法进行仿真，结果如图5所示。从图5中可以看出，NLMS算法的收敛速度略低于LMS算法，但是收敛后的误差信号比LMS算法小约2 dB。为了获得更好的预失真效果，可采用复杂度较高的NLMS算法，此算法适合在Zynq的处理系统(Processing System,PS)模块中实现[7]。而对于图4所示的预失真器实现，由于其不高的运算复杂度和并行运算需求，适合在Zynq中的可编程逻辑(Programmable Logic,PL)中实现。

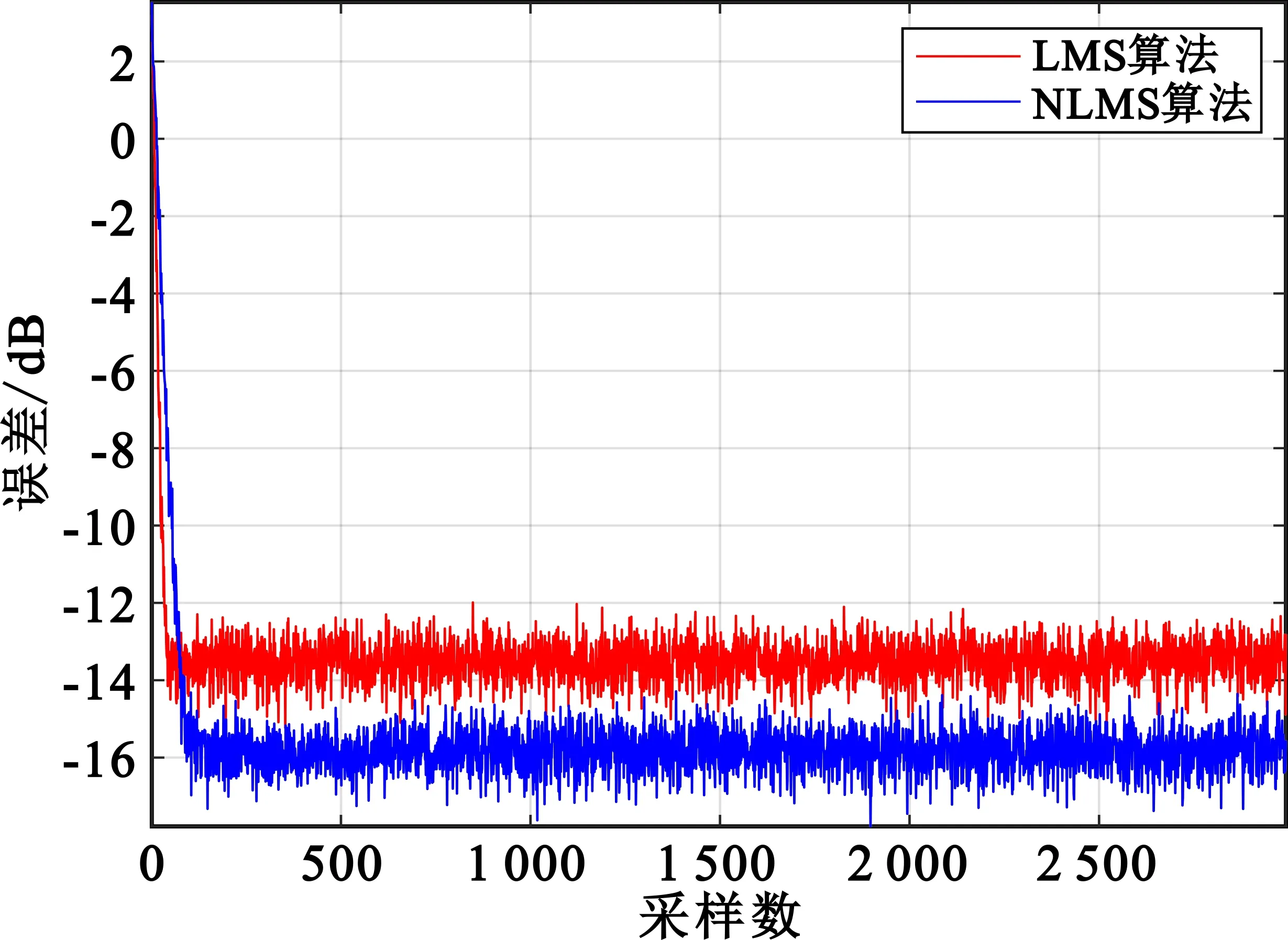
图5 LMS和NLMS算法收敛对比图

2.3 算法仿真

本节分别对正交频分复用技术(Orthogonal Frequency Division Multiplexing,OFDM)调制基带信号、未经预失真处理的基带信号和经过预失真处理后的基带信号的功率谱密度进行仿真。基带信号具有23.04 MHz的带宽、61.44 MHz的采样率，载波数量为23 040个。仿真后的功率谱密度图如图6所示，其中，功率谱密度的频率经过了归一化处理，其幅度也经过了一系列处理，使其总小于0 dB，以方便观察预失真效果。

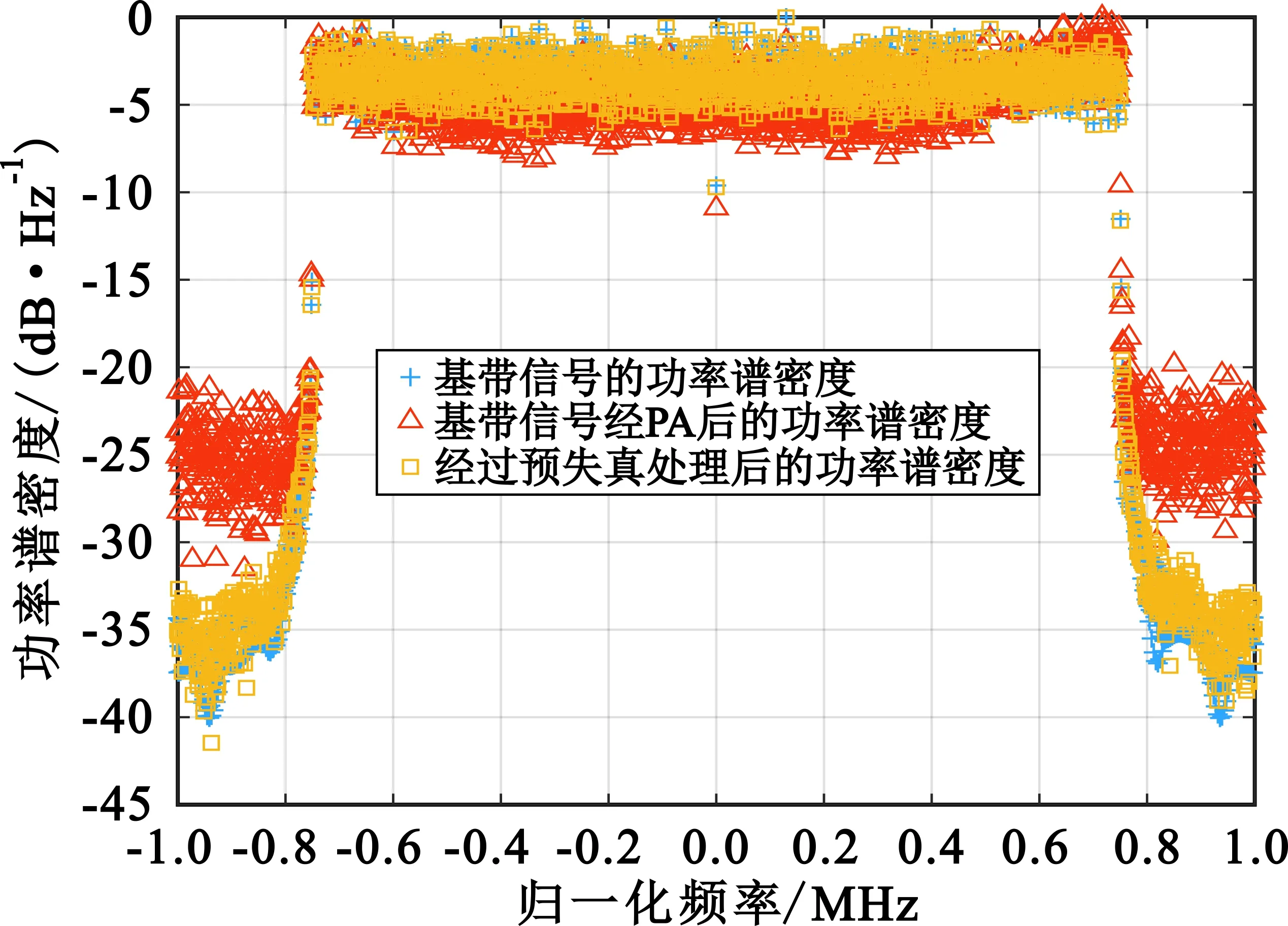
图6 功率谱密度对比图

从图6的仿真结果可以得出，经过预失真处理后的基带信号具有很好的带外抑制效果，改善了约10 dB的带外频谱增生，满足系统的需求；其ACPR也满足发射端系统的要求。

3 系统测试

根据图4所示的原理图，利用实验室现有设备，搭建起来的硬件结构如图7所示,包括频谱仪、二功分器、衰减器、功放和AD9361+Zedboard开发板。可以看出，此系统具有较高的集成度，且Zynq的双核处理器具有更强的数据处理能力，非常适合应用在DSP等高速处理模块上，同时PS和PL模块之间通过现成的AXI总线连接，相对于Microblaze软核降低了系统设计的复杂度，提高了系统的可重构性[8]。

图7 测试平台

射频器件选用的是AD9361，该器件的可编程性和宽带能力使其成为多种收发器应用的理想选择。该器件集RF前端与灵活的混合信号基带部分为一体，集成频率合成器，为处理器提供可配置数字接口，从而简化设计导入。在本设计中，AD9361的与Zynq的接口采用低电压差分信号(Low-Voltage Differential Signaling，LVDS)，在提高传输效率的同时降低了误码率[9]。

利用图7所示的测试平台，接下来对原始基带信号、未经预失真的功放输出信号和经过预失真的功放输出信号的功率谱密度进行测试，设置频谱仪的通道带宽(Channel Bandwidth)为3.84 MHz，分辨率带宽(Resolution Bandwidth)为100 kHz，显示带宽(Video Bandwidth)为1 MHz。图8为OFDM基带信号经AD9361上变频后输出的功率谱，调节功放放大16 dB后的输出信号如图9所示。可以看出，经过功放后的信号产生了较为明显的带外增生，会对邻近信道的信号传输产生较大的影响。

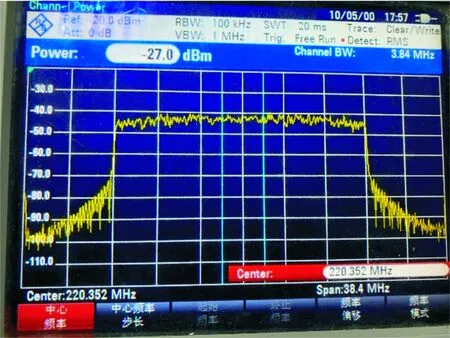
图8 原始信号

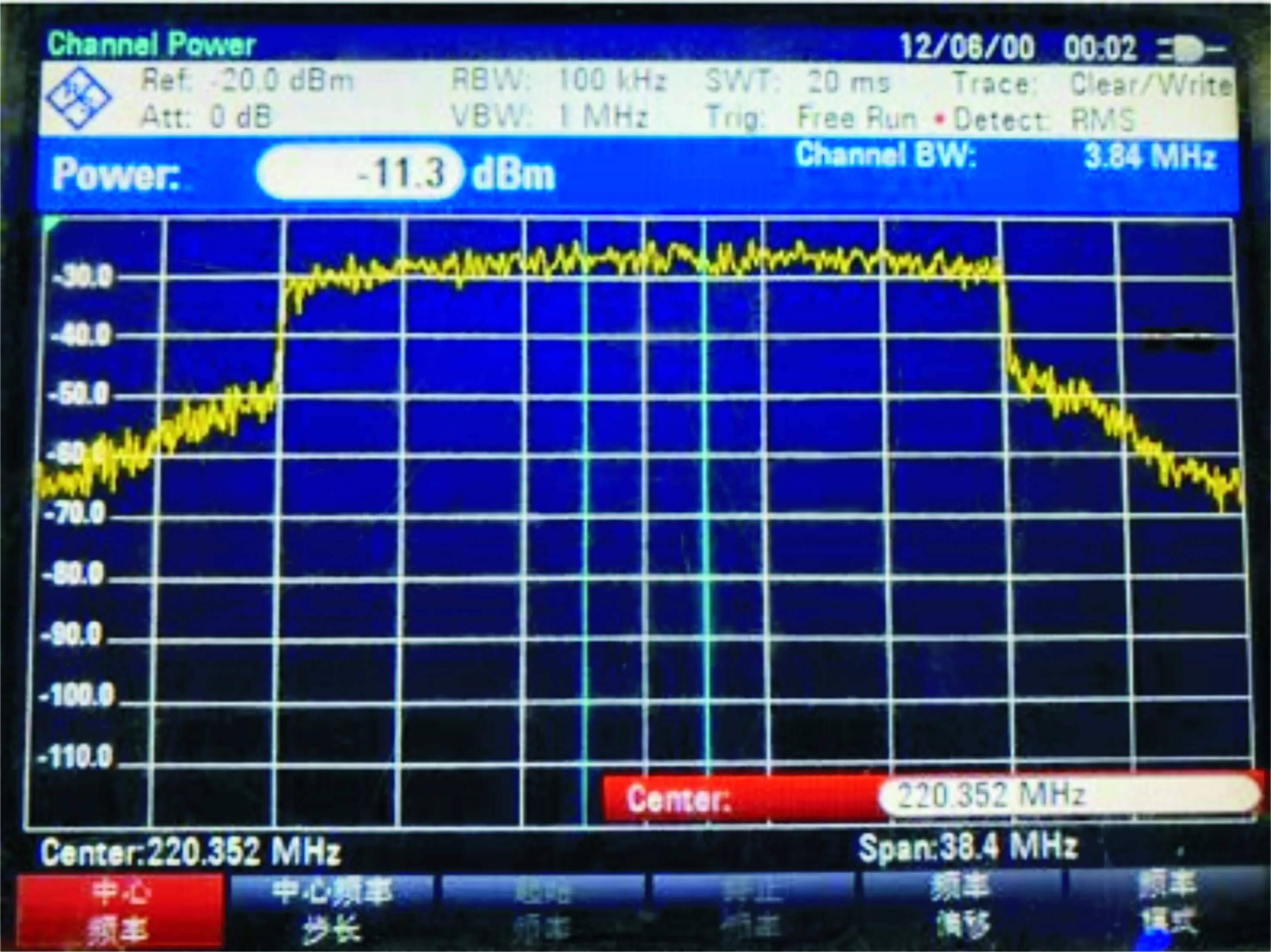
图9 未经预失真处理的功放输出信号

经预失真处理后的功放输出信号的功率谱密度图如图10所示，可经过预失真处理后，邻近信道的功率谱增生有了明显的改善，能够很好地抑制由功放产生的谐波所造成的频谱扩张，其ACPR比未经预失真的信号改善了10 dBc左右，达到了-45 dBc，完全满足系统的传输需求。

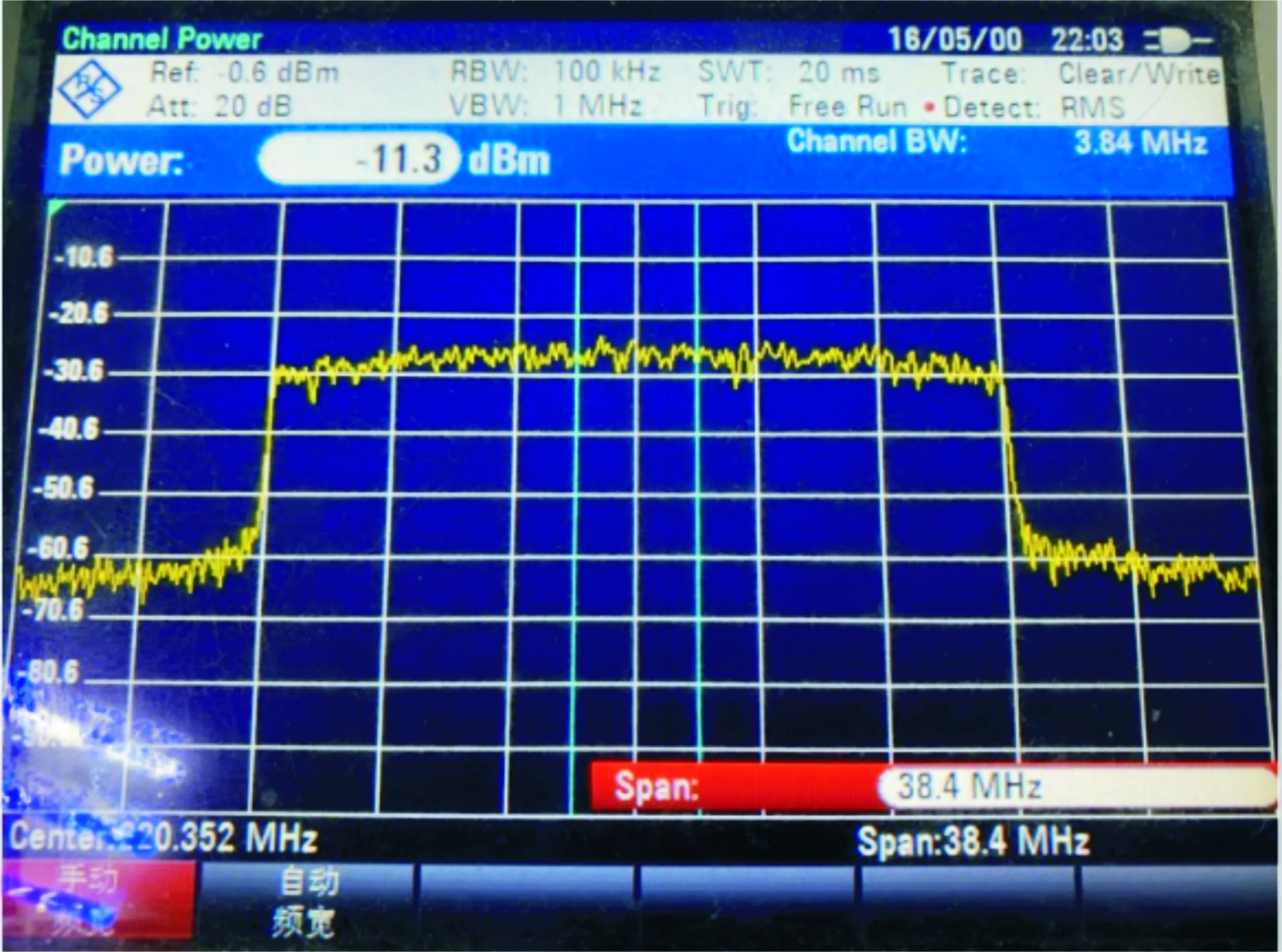
图10 经预失真处理后的功放输出信号

4 结束语

本文所提出的基于Zynq和AD9361的联合预失真架构相较于Microblaze+FPGA结构具有更高的集成度和性能。针对记忆多项式预失真模型，新提出的预失真器结构的硬件乘法器消耗相较于目前常用的多项式与查找表结构分别减少了Q个和2Q+3个，同时其运算周期相较于目前常用的记忆多项式与查找表实现方式分别降低了(3K-1)P与M个，一定程度上提高了系统的运算速度。自适应算法采用NLMS算法，在软件仿真中，其稳态误差比LMS算法小了2 dB。在实物测试中，采用以上结构的预失真系统和自适应算法，其ACPR达到了-45 dBc，改善了10 dBc左右，能够完全满足系统的需求。由于Zynq系统的板上资源丰富，今后可以研究在Zynq系统中实现拟合度更高、更复杂的数字预失真模块及其自适应算法。