基于Jarque-Bera检验的非线性多分布过程故障检测
郭小萍 俞巷天 李 元
(沈阳化工大学信息工程学院)
伴随着工业技术的飞速发展,越来越多的过程变量数据储存在仪器设备当中,如何提取数据中的有效信息实现工业过程的实时监视、故障检测成为研究的热点。 众多学者致力于面向复杂工业过程的更有效的故障检测算法的研究, 其中,数据驱动的多元统计方法受到广泛的关注[1,2]。
经典的基于主元分析 (Principal Component Analysis,PCA) 的故障检测方法是应用较广泛的一种数据驱动方法,其假设过程数据服从线性和高斯分布,但工业过程大多具有明显的非线性特征。Scholkopf B等为解决非线性问题,首次将“核”函数和PCA 结合形成最初的核主元分析(KPCA)[3]。 Lee J M等在20世纪初提出了基于改进平方预测误差的KPCA, 成功应用在连续过程故障检测中并取得有效的成果[4];同年又提出了一种基于多向KPCA的批量监控方法, 以青霉素多工况生产过程为实验验证了该方法的有效性[5]。He Q P和Wang J提出的基于k近邻故障检测方法适用于非线性特征的工业过程[6]。 郭小萍等提出了特征空间自适应k近邻方法, 有效地解决了故障检测模型不能及时更新的问题[7]。 He Q P和Wang J提出了基于主元k近邻方法, 成功地解决了计算过程复杂等问题[8]。
上述方法都是假设数据服从单一分布情况下的故障检测, 实际数据往往同时包含正态、非正态等特征,因此,国内外学者提出一些方法来对数据分布特征进行划分。 Jarque C M和Bera A K利用拉格朗日乘数法推导出有效的联合检验,形成最初的Jarque-Bera检验(J-B test),用于划分数据的正态性[9,10]。 Lee S等关于数据正态性划分给出理论推导, 证明J-B test相对于Kolmogorov-Smirnov检验和Bickel-Rosenblatt检验具有较高的适用性[11]。 Koizumi K等提出了一种基于威尔逊-希尔弗蒂变换的改进的Jarque-Bera检验(MJB),对高维数据的正态性划分具有很好的效果[12]。Bedok E和Yüksel M E提出一种基于J-B test的中值滤波器,极大地削弱了噪声数据的干扰[13]。Liu Y H等提出了一种基于J-B test的最优小波分解层数自适应确定算法,有效地减少了微小噪声的影响,提高了算法的精确度[14]。 Abdellatif D等提出将J-B test与k近邻(kNN)等相结合应用于人脸识别领域[15],用正态分布近似表示人脸区域具有良好的性能表现。 刘舒锐等将改进的J-B test与PCA和独立成分分析 (Independent component analysis,ICA)结合进行故障检测[16],但其忽略了在工业过程中不可避免的非线性问题。
为解决具有非线性和多分布特征的工业过程故障检测问题,笔者提出一种基于J-B test的故障检测方法。 基于J-B test和正态置信概率加权值将原始建模空间划分为正态子空间和非正态子空间, 然后在两个子空间中分别构建KPCA模型和kNN模型进行故障检测。 最后通过数值案例和TE过程仿真实验验证该方法的有效性。
1 核主元分析和k近邻方法简介
1.1 核主元分析
KPCA是一种非线性形式的主元分析法,其基本思想是利用非线性映射函数Φ将数据投影到高维特征空间F, 通过核函数有效地计算高维特征空间中的主成分, 再运用线性PCA技术完成故障检测[3]。
已知过程数据x=[x1,x2,…,xn]T∈Rn×m,通过非线性映射函数Φ:x→φ(x)投影后,数据在特征空间F的协方差为:

CF可以通过特征值分解对角化为:

其中,λ为CF的特征值,v为CF的特征向量。 所有λ≠0对应的特征向量vk,可以表示为特征空间F内相应映射点的线性组合:

其中,γ为特征向量vk的线性表示形式。
在式(2)两边同时点乘φ(xk)可得:

将式(3)代入式(4)中可得:

定义Kij=φ(xi)φ(xj)为核矩阵,将K代入式(5)化简得:

考虑到映射函数Φ是未知的, 为了方便运算引入核函数,笔者采用适用范围最广的高斯径向基核函数:
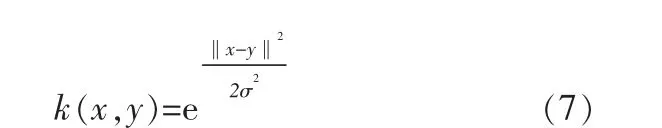
其中,σ为宽度参数,控制函数的径向作用范围。
原始样本x的映射数据φ(x)在特征向量vi上的投影为:

对于一个新样本,KPCA计算如下:
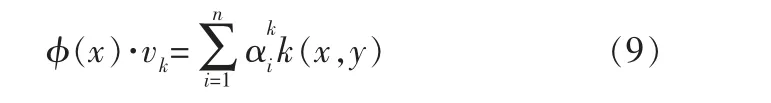
其中,k=1,2,…,q,q为主元个数。 KPCA使用的两个统计量分别由下式计算得到:

1.2 k近邻方法
kNN是一种有监督学习的分类方法, 适用于处理非正态分布的过程数据[17],其本质是观察样本间的差异性,故障样本具有的特征与正常样本的特征表现出很小的相似性[7]。 用样本x到其前k个近邻样本间累积距离的平方和作为统计量来表示特征,公式如下:

其中,dij为第i样本xi到其第j近邻样本xij的距离。

2 基于J-B test的非线性多分布故障检测
2.1 J-B test
已知n个独立样本的随机变量x=[x1,x2,…,xn]T∈Rn×1,变量的偏度S和峰度K可由下式求出:

在J-B test中,定义了一个服从卡方分布的统计量:

该统计量在默认置信水平α=0.05的基础上计算得到阈值, 假设被检测变量服从正态分布,若JB 统计量小于阈值,接受原假设,反之,则拒绝[18,19]。
由于标准正态分布的偏度S=0、 峰度K=3,所以若求出的样本偏度和峰度分别在0和3附近,则表示该样本正态性很强,也就是JB统计量应该趋于0,因而0值附近变量的正态性表现地并不是特别明显, 所以笔者对JB统计量取以e为底的对数再取负号,简称为-ln处理,使划分更加明确。 在Matlab环境中每个JB统计量都会伴随一个检验值p,笔者将其称为正态置信概率加权值,经过-ln处理后原始数据被划分为3部分:正态部分xn,正态性和非正态性性质均不明显的半正态部分xhn,非正态部分xnn。 利用正态置信概率值加权的形式,将半正态部分分别与正态部分和非正态部分结合成正态子空间和非正态子空间,即有:
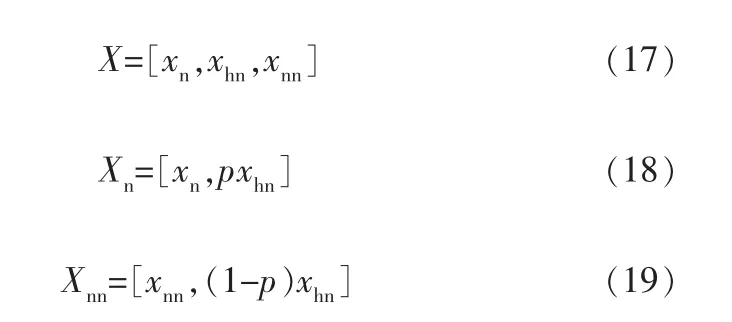
2.2 J-B test非线性多分布故障检测方法
离线建模步骤如下:
a. 采集正常训练数据集X;
b. 对标准化后的数据集进行J-B test,划分为两个部分;
c. 对JB统计量进行-ln处理, 数据被分为xn、xhn、xnn3部分,将每个部分的变量标记备用;
d. 通过正态置信概率加权值p, 获得正态子空间Xn和非正态子空间Xnn;

在线检测步骤如下:
a. 在线获取测试数据集Z;
b. 利用训练模型的均值、标准差对测试数据集Z标准化;
c. 通过训练模型变量的标记将数据分为3个部分——正态部分zn、 半正态部分zhn和非正态部分znn;
d. 利用训练模型的正态置信概率加权值p,获得正态子空间Zn=[zn,pzhn]和非正态子空间Znn=[znn,(1-p)zhn];
e. 在正态子空间中利用KPCA模型获得T2、SPE统计量, 在非正态子空间中通过kNN模型获得D2统计量;
f. 分别验证统计量是否超过其对应的阈值,低于阈值,表示该样本为正常,反之则为故障。
详细流程如图1所示。

图1 故障检测流程
3 数值案例仿真
笔者采用的数值案例由7个变量、2个潜隐变量(s1、s2)和7个噪声组成[17]:

其中,x1,x2,…,x7是变量,s1~U(-10,-7),s2~N(-15,1),e1,e2,…,e7是服从N(0,0.01)的白噪声。
该案例的变量划分如图2所示。
基于式(20)生成800个正常的训练数据并计算阈值;同时生成800个测试数据,在401~800数据处分别引入阶跃故障和斜坡故障。 为了验证笔者所提方法的有效性,分别对这两个故障用原始算法KPCA、kNN和改进后的算法JB-KPCA-kNN进行对比分析。
3.1 故障1——阶跃故障
在401~800数据处对变量x5加入幅值为0.1的阶跃故障。图3a、b是T2统计量的检测图,后者相比前者的检测率从84.25%提升到100%; 图3c、d是SPE统计量的检测图, 后者较前者的误报率从2.00%降低为1.00%;图3e、f是D2统计量的检测图,因为所加入的幅值较大,所以两者的检测率都能达到100%, 前者的误报率为7.25%, 后者为3.00%。
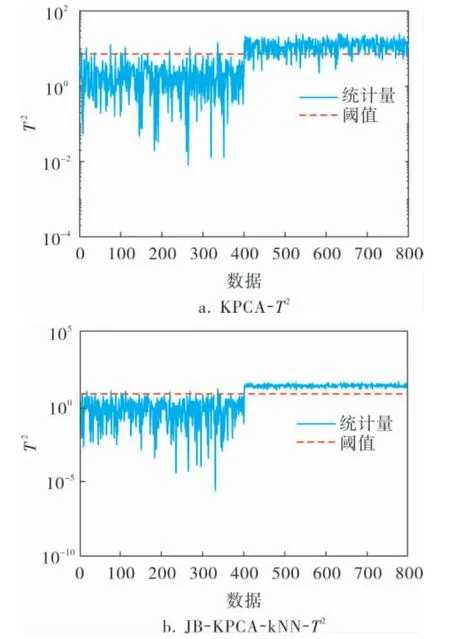

图3 阶跃故障的检测对比
3.2 故障2——斜坡故障
在401~800数据处对变量x2加入幅值为0.002的斜坡故障。图4a、b是T2统计量的检测图,因为加入的是斜坡故障且幅值较低,所以二者都出现延时报警的情况, 但是后者的检测率有明显提高,由前者的56.00%提升到82.75%; 图4c、d是SPE统计量的检测图,两者检测率都接近100%,但同样出现了延时报警的现象,并且发现后者的误报率从前者的1.75%降低为0.50%; 图4e、f是D2统计量的检测图,两者呈现较高检测率的同时都存在一定的误报率, 后者的误报率从前者的4.50%降低到3.00%,检测率从前者的95.75%提高到96.25%。两种故障的误报率和准确率见表1、2。

表1 两类故障的误报率 %


图4 斜坡故障的检测对比

表2 两类故障的检测率 %
从表1、2可以看出, 虽然KPCA和kNN对两种不同类型故障的检测效果较好, 但是JB-KPCAkNN的检测效果更加优秀, 该算法在保留很高检测率的同时也降低了误报率,虽然存在一些故障延迟报警的现象,但也是符合实际情况。
4 TE过程仿真
Tennessee Eastman(TE)过程(图5)是美国伊斯曼化学公司基于实际工业生产过程而研发的仿真平台。 该过程包含5个主要单元:冷凝器、反应器、分离器、压缩机和汽提塔,共有12个操作变量、22个连续测量变量和19个成分测量变量,该过程可预先设定21个故障[20]。
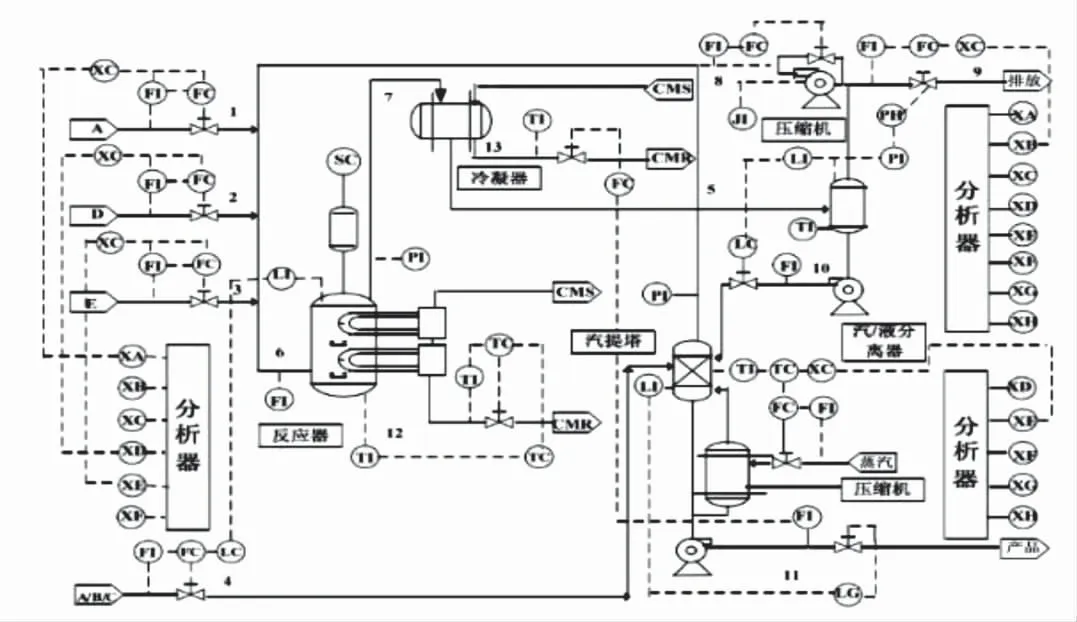
图5 TE过程流程
笔者采用52维变量的500个样本作为训练数据,通过J-B test和-ln处理后所有变量划分的结果如图6和表3所示, 图6中的红色虚线为JB统计量的阈值, 检测统计量的阈值都是基于置信度为95%而设定的。表4为半正态变量对应的正态置信概率加权值,在线检测时,选取960个数据作为测试数据,在161数据处加入故障。 以故障8为例,分别对比KPCA、kNN和JB-KPCA-kNN的检测结果并给出分析。

图6 TE过程的变量划分

表3 JB统计量划分结果

(续表3)
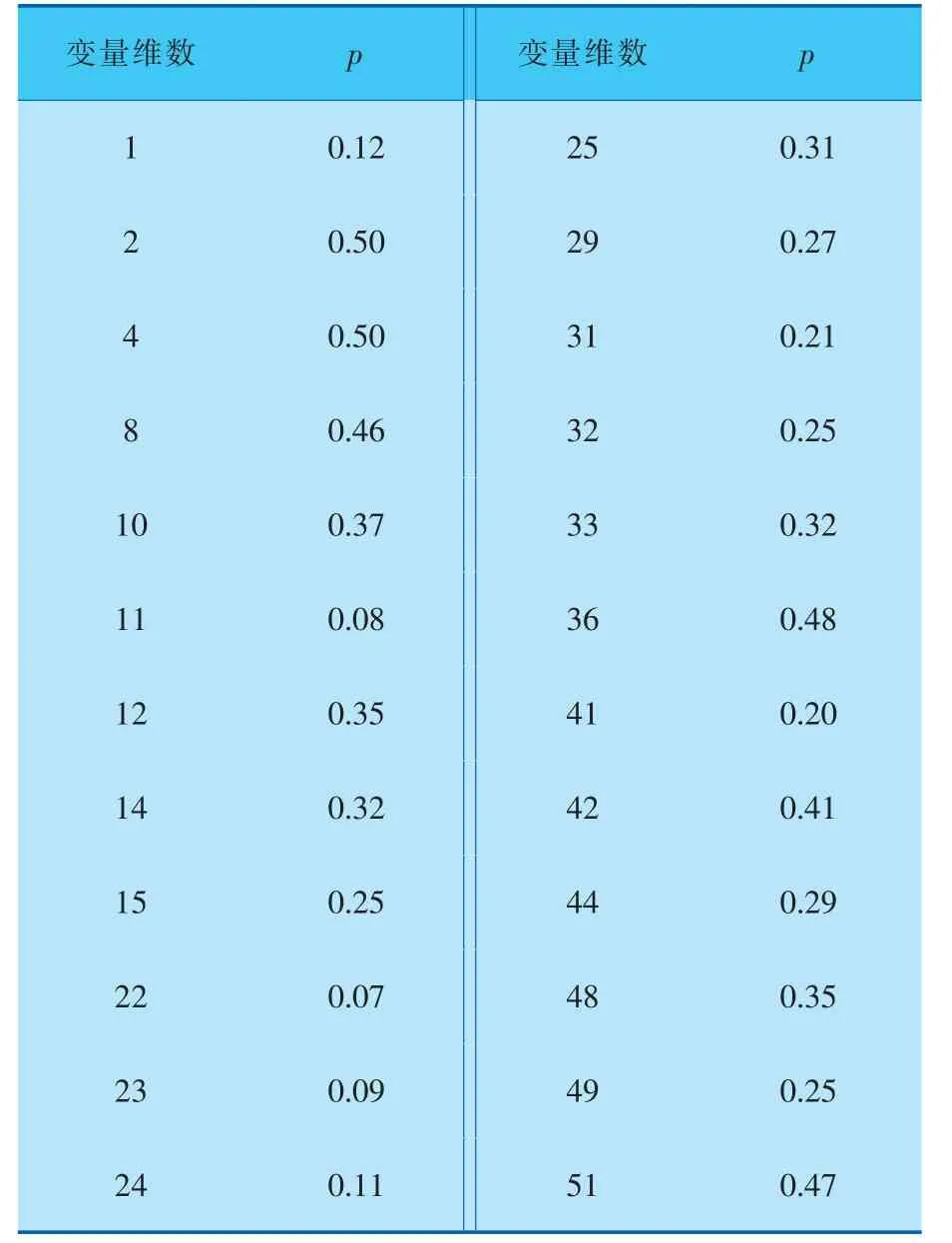
表4 半正态变量部分对应的正态置信概率权值
故障8是物料A、B、C的组成成分发生变化引起的故障。图7a、b是T2统计量的检测图,两者的检测率都很高, 但后者比前者的误报率从3.75%降低到0.63%;图7c、d是SPE统计量的检测图,后者较前者的误报率从19.38%降低为4.38%, 检测率从98.38%提高为98.63%; 图7e、f是D2统计量的检测图,两者的检测率都高达99.25%,但后者比前者的误报率从26.88%降低为18.13%。误报率和准确率数据见表5、6。

表5 TE过程故障的误报率 %
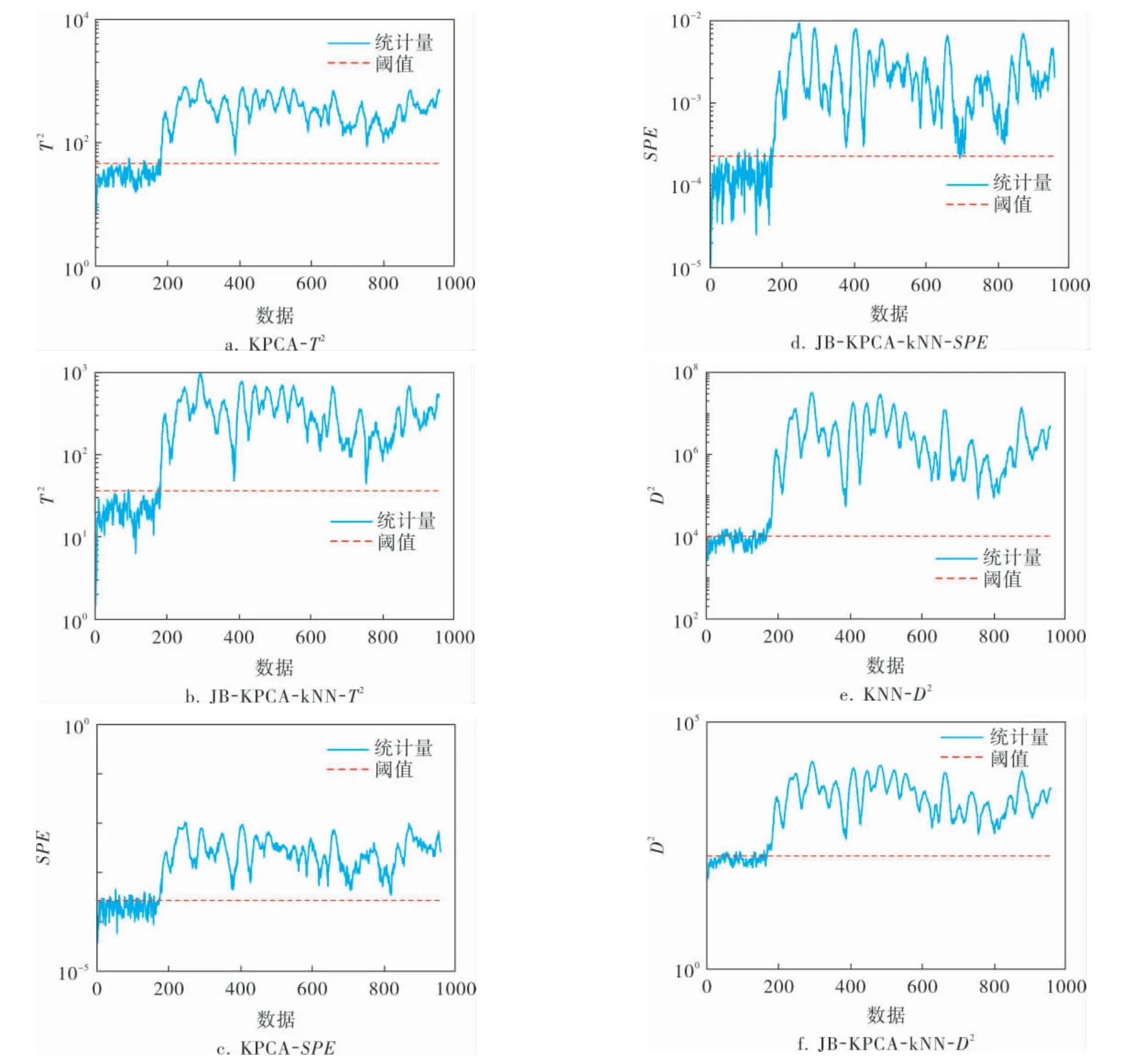
图7 故障8的检测对比

(续表5)

表6 TE过程故障的检测率 %
5 结束语
笔者提出了一种基于Jarque-Bera检验的非线性多分布故障检测方法,该方法能够全面提取系统过程数据的特征信息,使JB统计量对数据正态性的划分更加细致、完整,并针对性地用KPCA方法和kNN方法分别监测正态、 非正态分布的子空间,充分发挥了两种原始方法的优势。 仿真实验结果表明:所提方法有较高的检测率和较低的误报率,为非线性多分布工业过程提供了一种有效手段, 但也发现存在一些故障延时报警的现象,未来将针对此问题开展研究工作。

