基于改进条件生成对抗网络的分布式电源优化配置

胡 攀，邓 坤

（贵州大学 电气工程学院，贵阳 550025）

0 引 言

在节能减排和环境保护的背景下，以风力发电（wind turbine，WT）和光伏发电（photovoltaic，PV）为代表的分布式电源（distributed generation，DG）因其清洁环保、安装地点灵活、可提高供电可靠性等优点得到了快速发展。然而，由于WT和PV的输出功率存在较强的随机性，给配电网带来了一定影响，成为DG在配电网中发展的主要障碍。因此，科学地对DG进行规划对配电网的安全经济运行具有重要意义。

目前，DG规划问题已经开展了许多研究。文献［3-4］在模型中考虑多种类型DG的时序特性并在成本函数中充分考虑环境污染费用，搭建了DG社会年综合成本最小为目标的规划模型，利用智能算法进行求解。然而，上述模型中忽略了风、光和负荷的不确定性，最终得到的DG优化配置结果存在一定的不合理性。为了降低不确定性的影响，一些学者在进行优化配置时考虑源荷不确定性的影响。文献［5］考虑待规划地区的风、光和负荷的不确定性，采用拉丁超立方和快速向前选择法分别进行场景生成和削减，构建了以年综合费用最少为目标的DG规划模型。文献［6］采用概率密度建模的方法构造风、光和负荷的典型日出力数据，以经济性和环保性为目标，建立基于随机场景的DG多目标优化模型，并采用改进的非劣排序遗传算法对模型进行了求解。文献［7］基于蒙特卡洛模拟抽样得到间歇式新能源和负荷出力情况以解决间歇式新能源消纳及功率波动问题。

尽管上述文献在DG容量随机优化配置问题上取得了一定进展，但目前生成场景大多采用拉丁超立方和蒙特卡洛等抽样方法，而使用这些抽样方法之前需要事先假设数据服从特定的概率分布。生成对抗网络（generative adversarial network，GAN）提出后受到广泛关注，GAN不需要事先假设数据服从特定的概率分布，直接从数据中学习并生成新的数据样本。文献［9］虽然研究了单种类型DG出力场景生成问题，但忽略了在实际规划中存在不同类型的DG。文献［10］利用GAN模拟大量风光出力场景，再用K-medoids聚类得到若干典型场景，构建微电网容量随机优化配置模型，虽然考虑了DG的出力不确定性，但却忽略了DG的时序出力特性。

针对上述研究现状，为了避免传统抽样方法中假设的数据分布与真实数据分布不同而导致生成的场景不合理，本文采用改进的条件生成对抗网络模型无需事先假设原始数据分布，训练结束后即可生成与实际数据分布相近的风光出力场景。为了得到有效的规划场景集，使用K-means聚类算法进行场景聚类。然后构造了以年综合费用最小为目标的分布式电源优化配置模型，模型中充分考虑了政府补贴及环境污染等费用。由于模型中具有非线性项，通过二阶锥松弛方法将模型转换为混合整数二阶锥规划问题。用IEEE 33节点系统验证所提出规划模型的有效性。

1 改进的条件生成对抗网络

1.1 条件GAN模型

GAN是Goodfellow提出的一种深度学习模型，由生成器和判别器两个部分组成。其中，生成器通过学习真实数据的概率分布来生成新的样本。判别器则判断输入的数据是否为真实数据，两者通过博弈学习来提高生成样本的质量。条件GAN是在GAN基础上进行改进的一种生成式网络，是将监督学习和无监督学习相结合，并在模型的输入中添加了标签信息，可用于指导数据的生成过程，对指定类型数据样本的泛化有较好的效果，能够较好地适应风电和光伏出力场景构建问题。条件GAN的基本结构如图1所示。

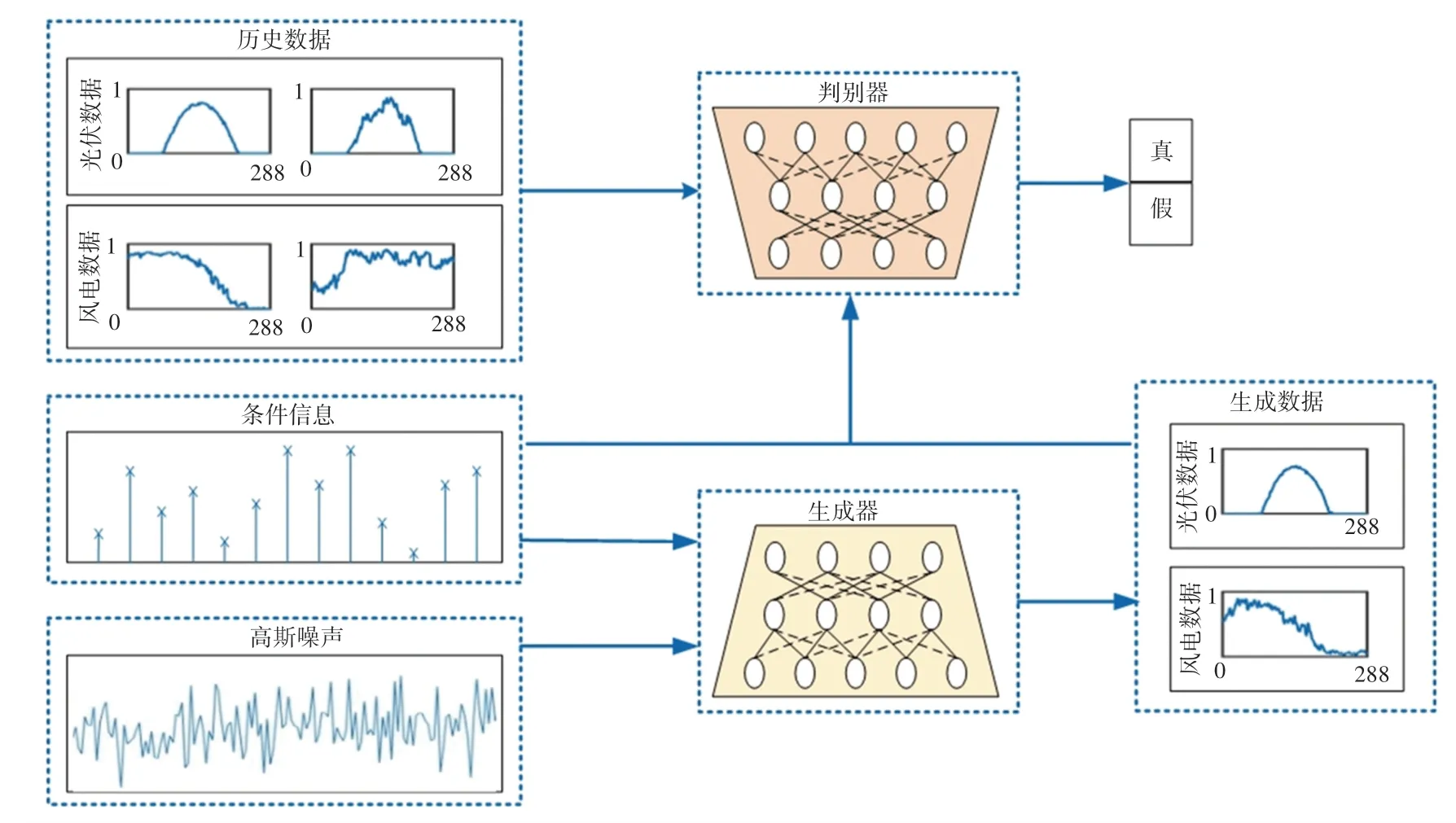
图1 条件GAN的基本结构Fig.1 Basic structure of conditional GAN

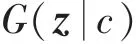
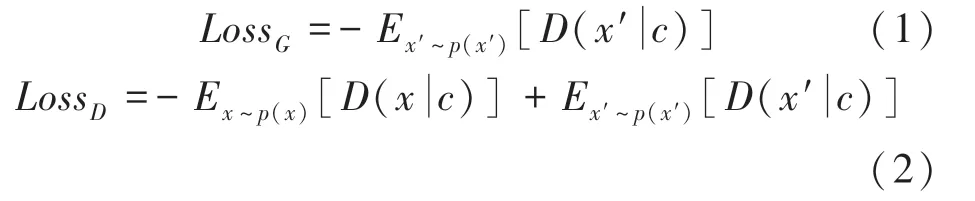
其中，为对应分布的期望值，（）为判别器函数。

在条件GAN训练的过程中，训练目标是带有条件的极小极大值博弈，如式（3）所示：

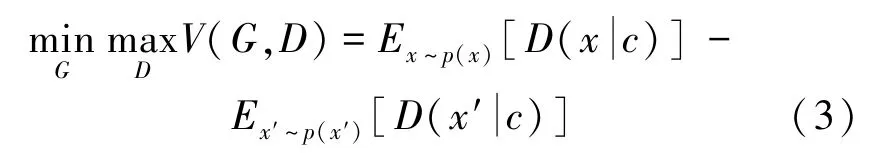
在训练结束后，生成器可学习到真实样本的概率分布特征，从而能在条件信息下生成服从真实规律的数据。

1.2 条件WGAN-GP模型

传统GAN在训练过程中容易出现训练困难和模式崩溃的问题，从而影响生成样本的准确性。为了避免上述问题，用Wasserstein距离的损失函数来替换传统GAN中的JS散度，Wasserstein距离可衡量2个不同概率分布之间的相似程度，其值越小代表2个概率分布的相似程度更高，其定义如式（4）所示：

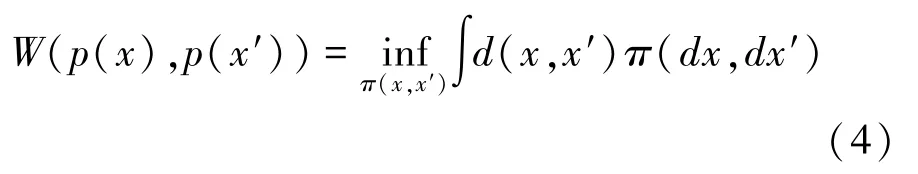
其中，（，）为满足（）与（）边缘分布的联合概率密度分布，（，）为场景间距离测度。

一般用Kantorovich-Rubinstein对偶形式对Wasserstein距离进行求解，当其应用于条件WGAN中时，如式（5）所示：

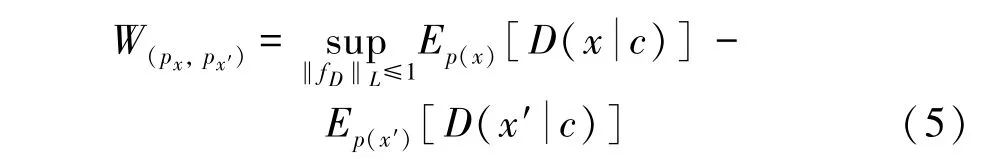
其中，‖f‖≤1表示判别器需满1-Lipschitz连续。

本文通过修正判别器的损失函数，在原有的损失函数中添加梯度惩罚项来使其满足1-Lipschitz条件限制，具体形式如式（6）所示：

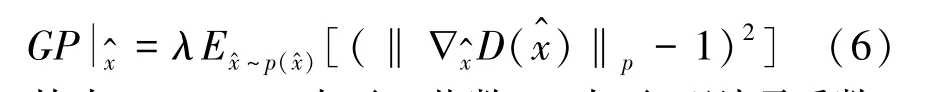
综上所述，条件WGAN-GP的整体训练目标函数为：

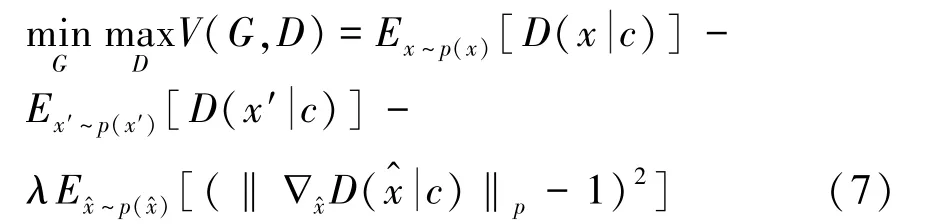
1.3 条件WGAN-GP结构设计

本文采用卷积神经网络代替传统的多层感知器来构建生成器和判别器，生成器和判别器为对称的网络结构。生成器共有4层，滤波器数量分别为256、128、64和1。第一层卷积核大小为5，后3层卷积核大小为4。前3层以作为激活函数，最后一层以作为激活函数。同时为了加快网络训练速度，提高网络的鲁棒性，在前3个卷积层后面均添加批量归一化（batch normalization，BN）层，考虑到BN层会是输出规范化到（0，1）的正态分布，因此输出层后不添加BN层。判别器也为4层，卷积核大小为4，滤波器数量分别为16、32、64和1。前3层以作为激活函数，由于条件WGANGP模型的结构特点，最后一层不添加激活函数。生成器和判别器的网络结构及参数分别参见表1和表2。

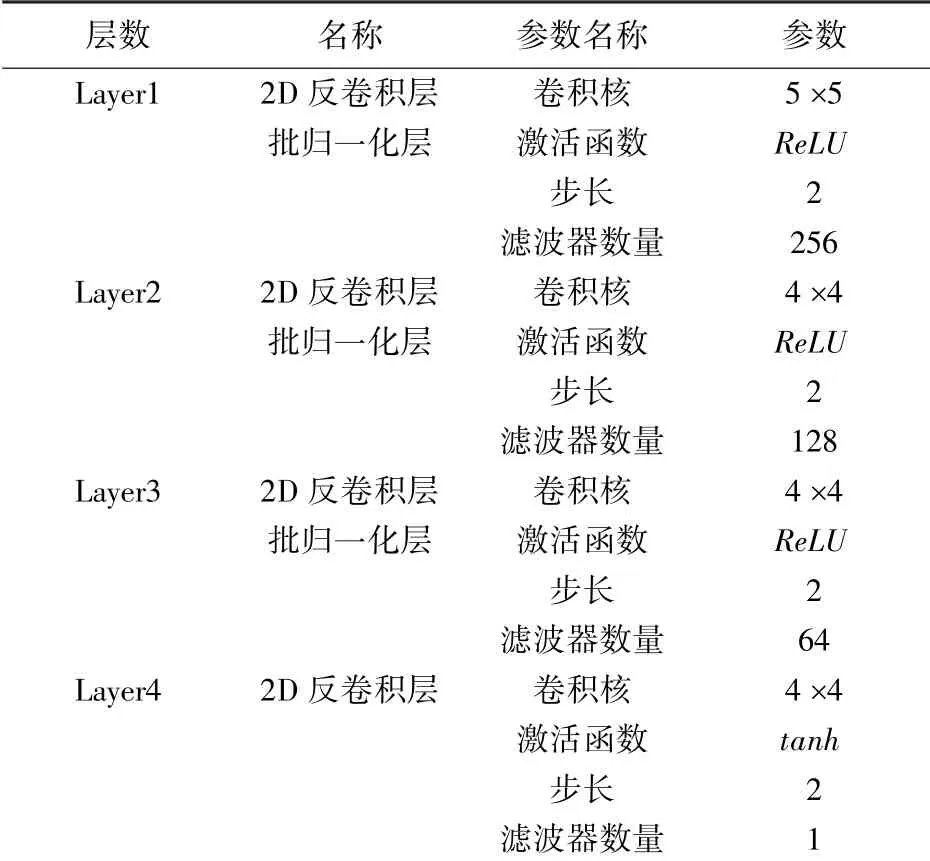
表1 生成器结构Tab.1 Structure and parameters of the generator

表2 判别器结构Tab.2 Structure and parameters of the discriminator

2 基于K-means的风光时序出力场景削减

由于风电和光伏出力有较强的随机性和波动性，随季节和天气的变化而变化，仅以某日数据值作为规划参数，不能体现风电和光伏出力的特点，会导致规划结果不合理。本文基于条件WGAN-GP学习风光历史数据的分布，生成大量1～12月风光出力场景集，但若利用全部数据进行大量的仿真计算，都将由于运算量巨大而导致求解困难，对于规划人员来说不可行、也无应用价值。因此，有必要对生成的大量风光出力场景进行聚类。

为了在减少计算量的同时充分考虑风光出力的时序性和随机性，本文采用K-means聚类算法对生成的风光出力场景进行聚类。根据一年4个季节，把不同季节下的风光出力场景聚类为晴、阴、雨三种典型场景，故聚类后共有12个场景，K-means聚类削减步骤如下。

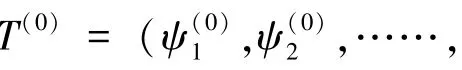
（2）分别计算每个场景到聚类中心的欧氏距离，并将每个场景划分到距离最近的聚类簇中。每个场景到聚类中心的欧氏距离的计算公式如下：

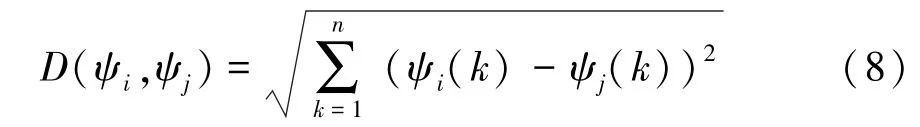
其中，（ψ，ψ）为场景曲线间的距离，ψ（）为第个场景的第维数据。

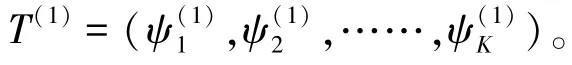
（4）重复步骤（2）和（3），最终的聚类中心曲线即对应个典型场景 {，，……，ξ。

3 考虑不确定性的DG优化配置模型

3.1 目标函数

本文以WT、PV和MT三种DG为研究对象，建立了年综合费用最少的DG优化配置模型，费用包括DG的建设投资费用、运行维护费用、网络损耗费用、主网购电费用以及DG发电产生的环境效益，具体形式如下：

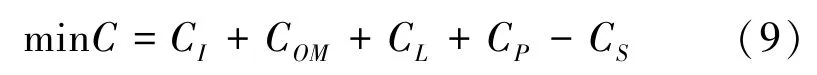
式（9）中，DG的各种费用的数学表达形式如下。

（1）折算到每年的DG建设投资费用C，其值可由如下数学公式计算得到：

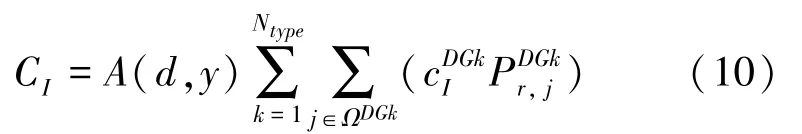
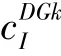
（2）DG年运行维护费用C，其值可由如下数学公式计算得到：

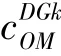
（3）网络损耗费用C，其值可由如下数学公式计算得到：

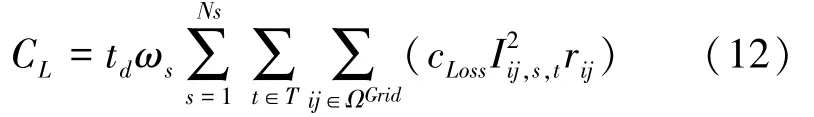
其中，Ω为所有节点集合；c为网损成本系数；I表示场景在时刻由节点流向节点的电流；r表示节点和节点之间线路的电阻值。

（4）向上级电网购电费用C，其值可由如下数学公式计算得到：

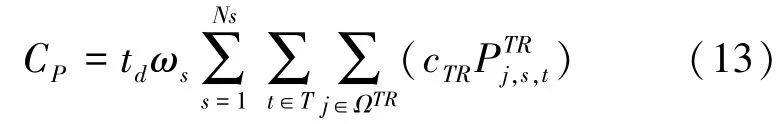
（5）DG发电环境效益C。 环境效益包括2个部分：环境污染费用和政府补贴。这里，环境污染费用是MT发电所产生的环境污染赔偿费用；政府补贴是DG发电所产生的效益。C值可由如下数学公式计算得到：

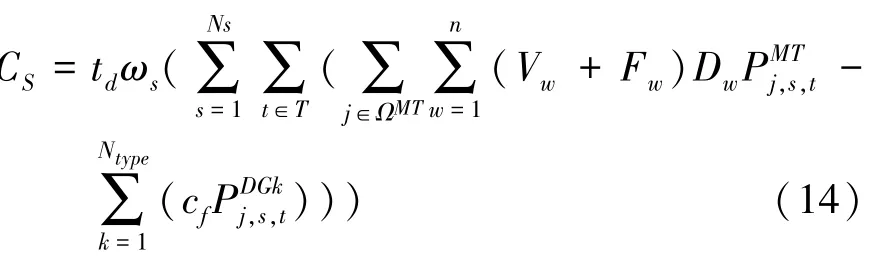
3.2 约束条件

（1）潮流方程约束

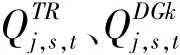
（2）节点电压约束

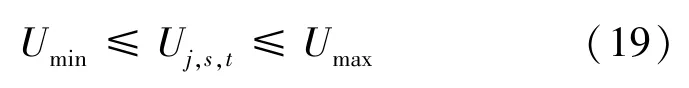
其中，和分别为节点电压的上限和下限。

（3）支路电流约束

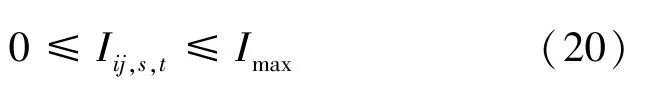
其中，为支路所允许的电流最大值。

（4）变压器节电功率约束

（5）DG相关约束

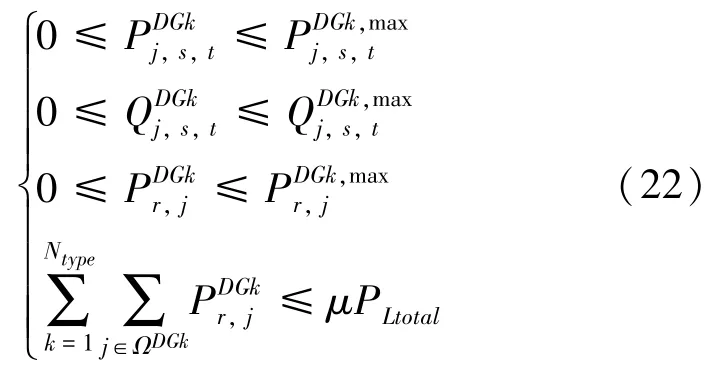
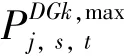
3.3 模型的二阶锥松弛处理

上述模型中，由于运行成本式（12）、潮流约束式（15）～式（18）存在非线性项，目标函数不容易求解，故需要将其线性化，令：

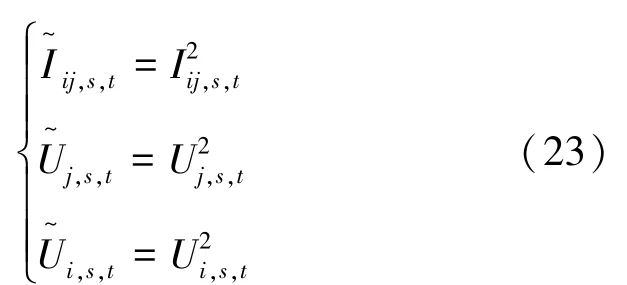
将上式带入得：

经过处理后上式仍存在非线性项，需要进行松弛处理，将其转化为如下所示的二阶锥形式：

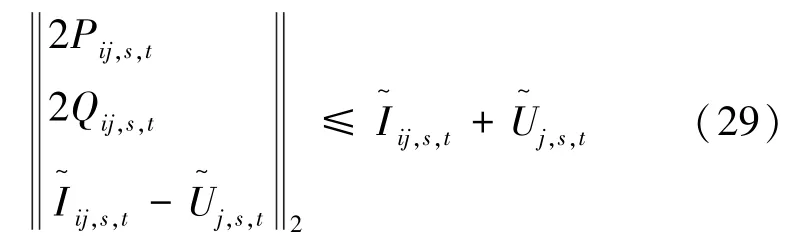
综上所述，原始模型中由于其非线性项难以求解，通过对非线性项进行二阶锥松弛后，转化为混合整数二阶锥规划模型，此时可利用商业软件CPLEX快速求解。

求解DG优化配置规划模型流程如图2所示。

图2 CPLEX求解DG优化配置模型流程图Fig.2 Solution flow of DG optimal allocation using CPLEX

4 算例分析

4.1 算例参数设置

本文通过IEEE33节点标准测试系统进行验证，系统参数见文献［17］。IEEE33节点配电网结构如图3所示。

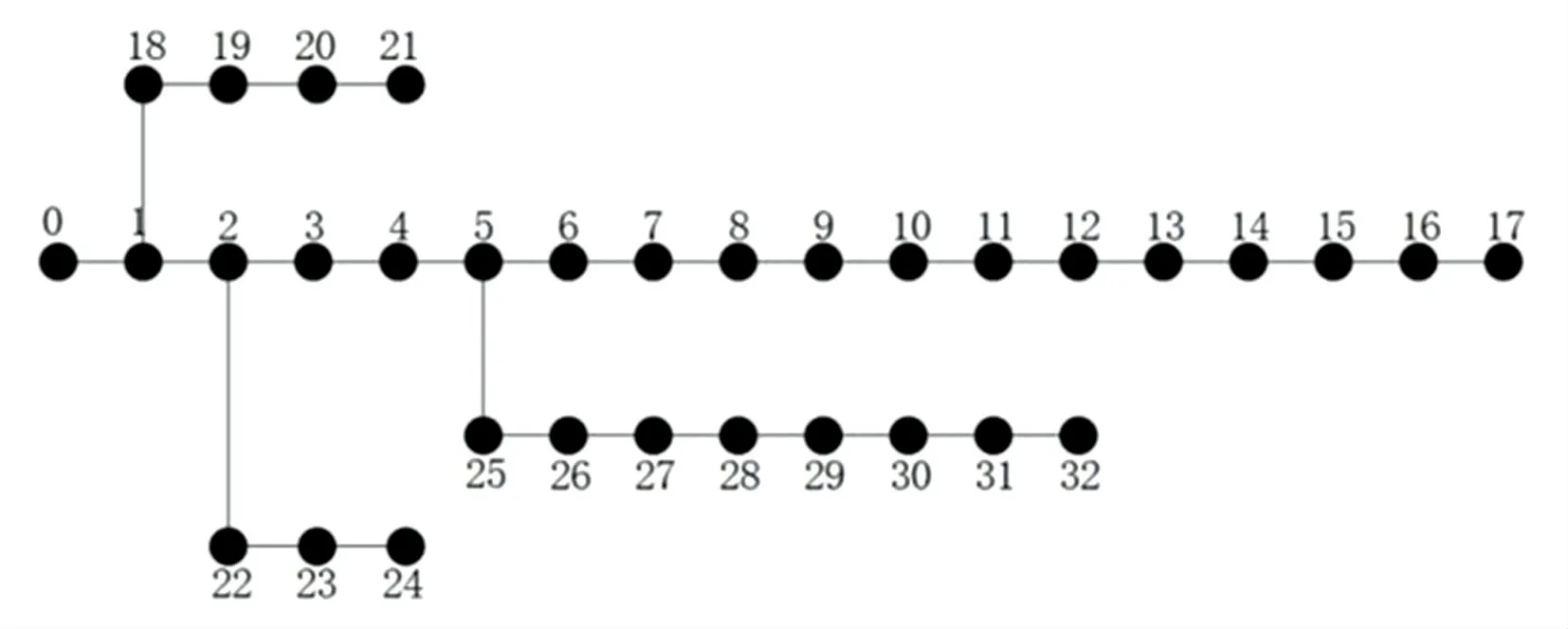
图3 IEEE33节点配电网结构Fig.3 Structure of IEEE 33-bus distribution network

算例参数参见文献［18-20］。本文以风电、光伏和微型燃气轮机作为DG的代表。风电的候选安装节点为4、7、17、28，光伏的候选安装节点为13、20、24、32，微型燃气轮机的候选安装节点为29、30。规划年限为20年，贴现率为0.06。配电网向大电网单位购电成本为0.5元/（kWh），DG的渗透率为35%。不同类型DG的建设投资成本、运行维护成本和DG发电政府补贴见表3。MT的污染物排放数据见表4。

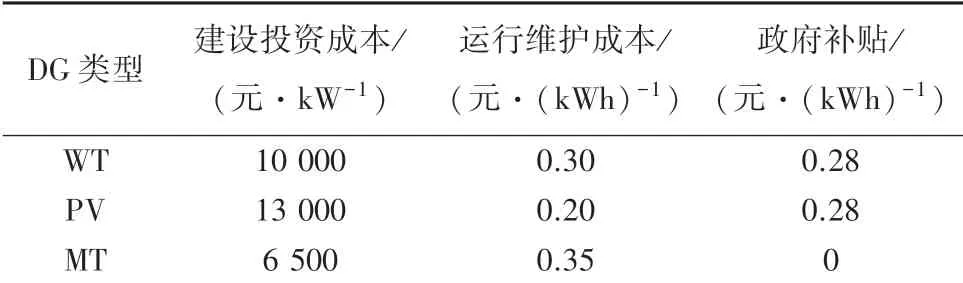
表3 DG单位成本Tab.3 DG unit cost

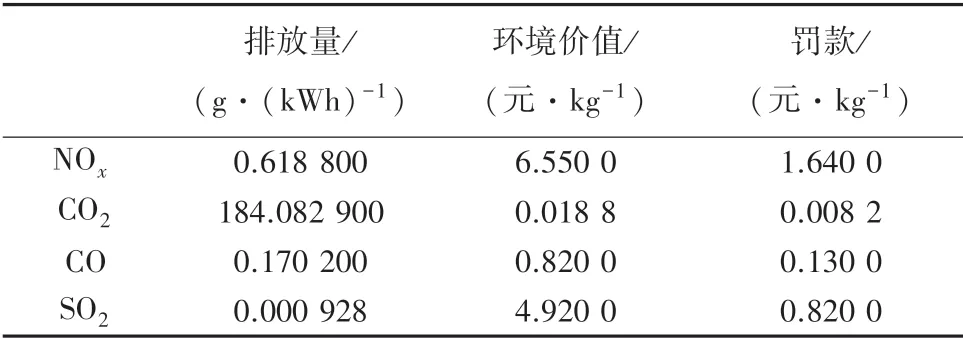
表4 MT污染物排放数据Tab.4 MT pollutant emissions data

4.2 条件WGAN-GP场景生成模型分析

本文基于PyTorch深度学习框架搭建条件WGAN-GP模型，算例中风光出力数据来源于美国的NREL实验室。图4和图5分别是条件WGANGP训练过程中生成风电和光伏出力的效果图。

图4 基于条件WGAN-GP的风电出力效果图Fig.4 Effect graphs of wind power output based on conditional WGAN-GP

图5 （a）～图5（d）分别是条件WGAN-GP训练过程中迭代0、100、200、300次的效果图。迭代次数为0时，由于还未开始训练，尚未学习到原始数据的分布特征，生成的风光出力曲线为随机波动的白噪声。随着迭代次数的增加，生成器不断地学习，进而生成的风光出力数据质量逐渐地增高，达到100次和200次时，从图5（b）和图5（c）可以看出，生成的数据已经具有了一些风光出力周期性变化的特征，而且明显可以看出，由于图5（c）迭代次数更多，生成器学习到更多的风光出力特征，因此生成的数据质量要比图5（b）更高，但此时仍未充分捕获风光出力数据的内在特性。当迭代次数达到300次时，生成器与判别器达到动态平衡，此时生成的风光出力曲线较平滑。可以看出，本文使用的条件WGANGP模型能较好地学习到风光出力的特征，生成符合真实规律的风光出力数据。

图5 基于条件WGAN-GP的光伏出力效果图Fig.5 Effect graphs of photovoltaic power output based on conditional WGAN-GP

为进一步验证生成的风光出力数据的有效性，通过绘制风光的真实数据与生成数据的累积概率分布函数，如图6和图7所示。从图6、图7中可以看出，生成的数据的概率分布和实际数据的概率分布十分接近，这表明了本文基于条件WGAN-GP生成的风光出力数据是合理的。

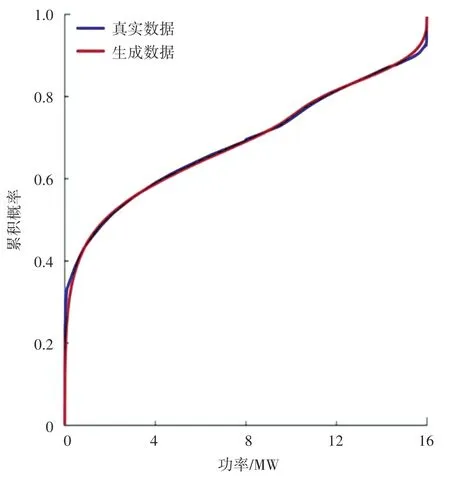
图6 风电生成数据和真实数据的概率分布比较Fig.6 Comparison of probability distribution between wind power generation data and real data

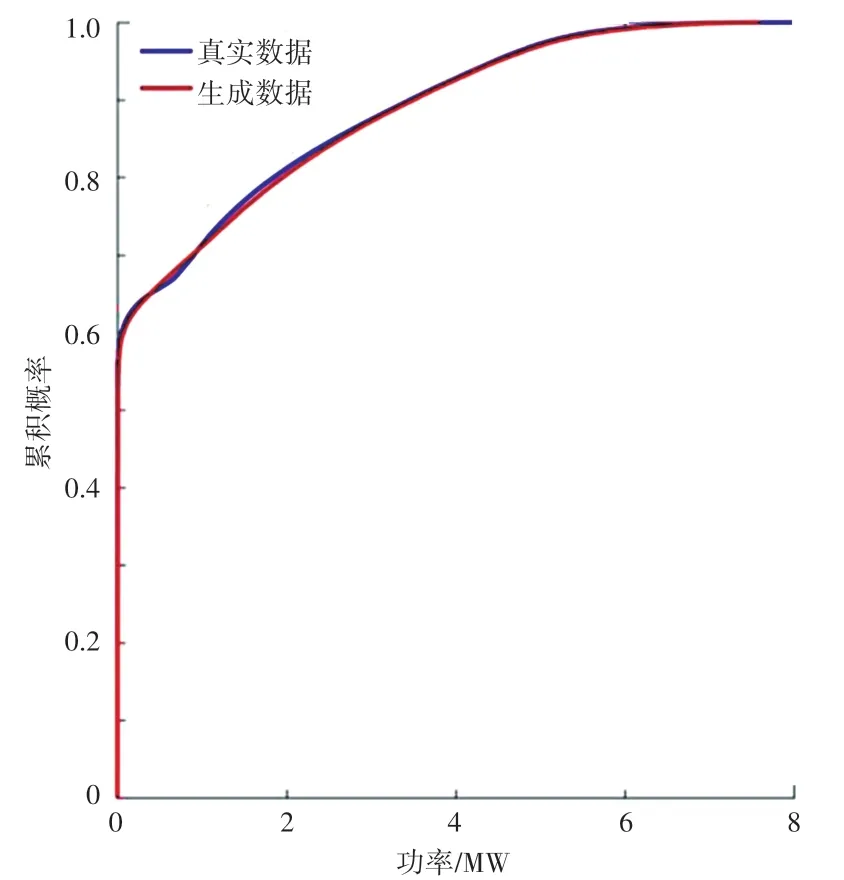
图7 光伏生成数据和真实数据的概率分布比较Fig.7 Comparison of probability distribution between photovoltaic power generation data and real data

4.3 优化规划结果分析

本文设定了3种不同的方案进行比较，分述如下：

（1）方案1。为在本文所提出规划方案下安装DG。

（2）方案2。为在负荷水平较高的节点多安装DG，但每个节点的DG接入容量不超过该节点80%的负荷。

（3）方案3。为不安装DG，仅由上级电网向本系统供电。

规划结果见表5，在风机、光伏和微型燃气轮机配置结果中，括号外的数字代表DG的安装节点，括号内的数字代表DG在此节点的安装数量。

通过分析表5，可以得出以下结论：

表5 规划结果Tab.5 Planning results

（1）从方案3的结果可以看出，配电网的网损费用54.30万元，向上级电网购电费用为1 078.74万元，社会年综合成本为1 133.04万元，明显均高于方案1和方案2。这表明DG接入配电网能提升配电网运行的经济性。

（2）与方案2和方案3相比，采用本文所提出规划方法的方案1网损费用最低，这是由于通过在配电网中合理配置DG，减少了配电网中潮流的流动，有效地降低了网损。

（3）从方案1中DG的配置结果可看出，DG更多地安装在线路的末端。这是因为当首端电压一定时，线路末端电压水平难以维持在所允许水平内，而接入DG后，能很大程度上提高线路末端电压水平，减小线路首端和末端电压差，满足系统电压要求。

（4）考虑风光出力不确定性是合理的，相比于将其视为确定性的方案，与实际情况更加贴近，可实现总体运行成本最低，且可以较大地减少社会年综合费用。

5 结束语

本文采用多场景分析法对DG容量规划当中的不确定因素进行处理，然后构造了以年综合费用最小为目标的分布式电源优化配置模型。利用IEEE33节点配电系统进行仿真验证，实验结果表明所构建模型的有效型。得到结论如下：

（1）提出使用条件WGAN-GP模型生成风光出力场景集，用K-means聚类算法对场景进行削减。简化了建模和计算的复杂度的同时，充分考虑风光出力的时序性和随机性。

（2）算例结果表明，通过条件WGAN-GP模型生成的风光出力数据的概率分布和真实数据的概率分布十分接近，克服了传统抽样方法中假设的数据分布与真实数据分布不同而导致生成的场景不合理的问题。

（3）DG优化配置结果表明，DG接入配电网能明显减少社会年综合费用。与其他规划方案相比，本文所提出方案成本最低且更为合理。有利于未来DG进一步的推广和发展。