寻找动点中的全等三角形
张君翔

全等三角形和動点相结合往往会产生意想不到的效果,这时,只知道全等三角形的5种判定方法已经远远不能满足解题的需要。因此,本文选取两个例题来进行探究,希望对同学们有所帮助。
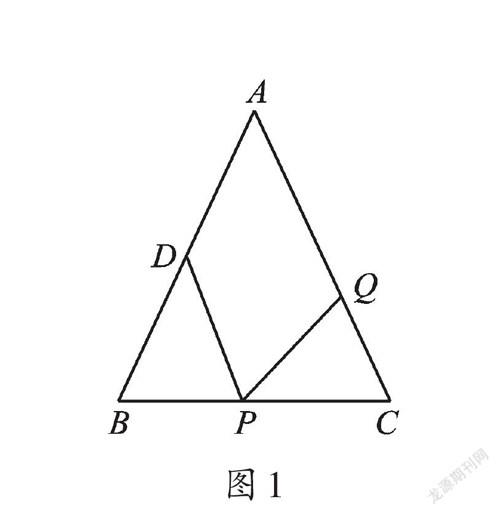
例1 如图1所示,△ABC中,AB=AC=12cm,BC=9cm,点D为AB边上的中点,如果点P在BC边上以3cm/s的速度由B向C运动,同时点Q在CA边上由点C向点A运动。
(1)若点Q的速度与点P的运动速度相等,1秒钟时,△BPD和△CQP是否全等,请说明理由;
(2)若点Q的速度与点P不相等,点Q的速度为多少时,△BPD和△CQP全等?
【解析】本题是以一个等腰三角形为背景,在两个动点运动的过程中,产生三角形全等。题目已经明确了要证明的全等三角形,接下来就是要分析两个三角形中的相等条件。
(1)如图1,因为在等腰△ABC中,AB=AC,所以∠B=∠C,这是本题中始终存在的相等条件,和动点的运动无关。1秒钟时,因为点P的速度和点Q的速度相等,所以我们可以求出两个动点的运动路程,即线段BP和线段CQ的长度,均为3cm,线段PC的长度是6cm,因此可以得到全等的三个相等条件,即BD=PC,∠B=∠C,BP=CQ,所以△BPD≌△CQP。
(2)首先∠B=∠C是仍然成立的,但是此时与第(1)问中不同的是点Q和点P的运动速度不同,那就说明BP≠CQ,那如果三角形△BPD和△CQP全等,则必然会有对应相等的关系。根据“相等即对应”,我们可以分析得出B点与C点对应,P点和Q点是不对应的,那么只可能是点P与点P对应,点D与点Q对应,即△BPD≌△CPQ,则有BP=CP,BD=CQ,通过这两组边相等,先求出BP=4.5cm,t=1.5s,CQ=6cm,所以点Q的速度为4cm/s。
例2 如图2,在四边形ABCD中,BC=AD=10cm,AB=CD,BD=14cm。点E从D出发,以2cm/s的速度沿着DA向终点A匀速运动,点F从点C出发,以5cm/s的速度沿着C→B→C匀速运动,点G从B点出发,向终点D匀速运动。三点同时出发,当有一个点到达终点时,其余两个点也随之停止运动,设运动的时间为t秒。
(1)证明AD∥BC。
(2)在移动的过程中,有没有△DEG与△BFG全等的情况出现?请探究这样的情况会出现几次,分别求出此时的运动时间t和G点的运动速度。
【解析】本题是在一个平行四边形背景中的动点问题。题目中一共有三个动点,要证明△DEG与△BFG全等,首先分析这两个三角形中已经存在的相等条件,然后讨论这两个三角形全等分类的标准,从而确定动点的运动情况。
(1)要证明AD∥BC,只要证明四边形ABCD是平行四边形即可。
(2)由(1)可得∠GBC=∠ADB,那么△DEG与△BFG就有一对角对应相等,围绕这一对角相等产生的全等,考虑是“SAS”全等的情况,也就是在BG、BF和DE、DG中出现两组边相等,那就有2种可能,即①BG=DE,BF=DG或者②BG=DG,BF=ED。设G点的速度为xcm/s,则BG=xt,DG=14-xt,DE=2t,因为C点是从C→B→C,所以BF=10-5t(0≤t≤2)或BF=5t-10(2 以①为标准的全等可列出方程组 [xt=2t,10-5t=14-xt(0≤t≤2),]或者 [xt=2t,5t-10=14-xt(2 第一个方程组解得x=2,t=[-43](舍);第二个方程组解得x=2,t=[247]。 以②为标准的全等可列出方程组 [xt=14-xt,10-5t=2t(0≤t≤2),]或者 [xt=14-xt,5t-10=2t(2 第一个方程组解得x=[4910],t=[107];第二个方程组解得x=[2110],t=[103]。 故全等的情况会出现3次,分别是当t为[247s]、[107s]、[103s]时,G点的速度分别是2cm/s、[4910cm/s]、[2110cm/s]。

