基于VMD-WVD相位法的长电缆局放双端定位

陈皇熹， 方春华， 普子恒， 吴田

(三峡大学电气与新能源学院，湖北 宜昌 443002)

0 引言

局部放电(partial discharge,PD)监测是一种评估电缆绝缘状态的重要方法。该方法通过分析检测PD信号，对PD源位置进行快速准确定位，从而保障电力系统的稳定运行[1—3]。

目前国内外针对电力电缆PD定位的研究较多，电力电缆故障检测手段以行波法为主。时域反射法(time domain reflectometry,TDR)是应用最为广泛的一种单端行波法，被应用于地质勘查、线路测距及PD定位等[4—6]。运行中电缆系统一般长达数千米甚至数十千米，而电缆中的反射信号最长传播距离为近2倍电缆长度。因此，信号易受到衰减和色散影响，导致反射信号畸变，影响TDR定位精度[7—8]。为提高TDR定位精度，文献[6]提出一种利用局放信号小波变换各尺度中心频率对应的波速进行定位计算的算法。文献[9]提出一种基于行波法的振荡波电压下电缆局放自动定位算法，该算法自动从PD波形中分离脉冲信号段，提取每个脉冲信号段的特征，进行入射信号和反射信号的匹配。文献[10]基于经验模态分解与动态时间规整算法，对原始局放波形进行局放脉冲分割和入反射脉冲匹配，最后根据TDR原理计算局放源位置。文献[11]利用一种改进相位差法，计算最初2次局放信号波峰时刻和信号波速以定位局放故障。上述研究充分考虑反射信号识别困难，并在短距离电缆下验证了定位精度，然而在长电缆中反射信号畸变严重，入、反射信号匹配难度大，定位精度还有待考证。针对长电缆中TDR入、反射信号匹配困难的问题，双端行波法被广泛用于故障定位[12]。该方法只须采集首次到达两端的信号，易于检测且准确度较高，能有效避免长电缆中入、反射信号匹配困难的问题。然而，双端行波法需用到精度极高的同步时钟，在现有技术条件下即使采用全球定位系统(global positioning system,GPS)技术，时间测量也存在同步偏差[8,13]。由于长电缆中信号传播时间更长，定位精度受时间影响更大，故准确同步两端故障信号波头时刻是双端行波定位法的关键所在[14]。

为此，文中提出一种基于变分模态分解(variational mode decomposition,VMD)-维格纳威尔分布(Wigner-Ville distribution,WVD)相位法的电缆局放双端定位。VMD是一种非递归分解模型，能反映信号奇异性特征，具有稳定性好、运算效率高和良好鲁棒性等优点[15—17]。WVD有优良时频分辨率和数学特性，能较好描述信号的边缘特征、瞬时频率等，并确定信号突变发生时间、频率及能量等信息[15,18]。将VMD-WVD相结合的相位双端定位只须在电缆两端安装传感器，采集局放入射信号，即可准确提取局放信号波头相位定位，从而使双端信号同步。该方法可有效解决传统行波定位法在长电缆局放定位中反射信号识别困难和时间同步误差的问题。

1 VMD-WVD相位法的电缆局放双端定位

1.1 理论基础

VMD可将局放信号分解为一系列有限带宽固有模态函数(intrinsic mode function,IMF)，分解后的IMF包含大量故障信息[19]。VMD核心是解决变分问题，约束局放信号变分问题模型如式(1)所示。

(1)

式中：∂t为对时间t偏导；δ(t)为冲激函数；uk为分解得到k个局放信号模态函数；K为最大分解层数；ωk为各模态函数中心频率；f(t)为局放信号。

引入Lagrange乘数法和惩罚因子α，解决式(1)有约束最优化问题，并通过交替方向算法迭代优化序列，得到局放信号模态函数及中心频率表达式如式(2)和式(3)所示。

(2)

(3)

利用式(4)对局放信号模态函数和中心频率进行更新。

(4)

式中：λ为Lagrange乘数因子；σ为更新因子。迭代式(2)—式(4)，满足式(5)所示收敛条件时停止迭代。

(5)

式中：ε为收敛标准容差。

由式(1)—式(5)可知，VMD使用迭代搜索变分模型最优解，确定局放信号模态函数及其中心频率，最终局放信号自适应分解为k个IMF。

WVD定义为信号瞬态自相关函数的傅里叶变换[20]，如式(6)所示。

(6)

式中：τ为信号时延；f*为f的共轭。对式(6)两边分别进行ω，t积分可得：

(7)

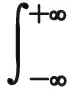
(8)

由式(7)、式(8)可知，局放信号在t时刻的WVD瞬时能量分布等于沿ω轴积分；局放信号在ω时刻的WVD瞬时能量分布等于沿t轴积分。

1.2 VMD-WVD相位法双端定位

使用VMD算法对局放信号分解，需预设VMD的分解层数k，其取值将影响分解结果。分解层数太少，会导致信息缺失；反之会出现频率混叠。文中采用基于能量差的自适应VMD算法确定VMD的分解层数[21]，VMD-WVD波头时刻提取主要步骤如下。

(1) 初始化分解层数k=2，设置K=10；

(2) 对局放信号进行k层VMD，计算局放信号的能量及各层IMF的能量；

(3) 从k=2开始逐层计算能量差参数ρ直至预设最大模态数；

(4) 定义能量差绝对变化率β，选取β出现最大值前对应的k作为最终分解层数，选取IMF1作为局放信号特征分量；

(5) 使用WVD求出该IMF的WVD瞬时能量分布，WVD瞬时能量分布幅值时刻即为局放信号波头时刻。

数字采样后的局放信号为离散信号，设局放信号为f(n)，对f(n)进行快速傅里叶变换如式(9)所示。

ffft(n)=Re(ffft(n))+Im(ffft(n))

(9)

式中：ffft为f的快速傅里叶变换。求得相位响应如式(10)所示。

(10)

重复式(10)可得各个点的相位谱。考虑局放信号传播过程的相位衰减特性，在电缆首、末端局放信号相位如式(11)和式(12)所示。

φ1=φdβ1

(11)

φ2=φ(l-d)β2

(12)

式中：φ为原始局放信号波头相位；φ1，φ2分别为电缆首、末端局放信号波头相位；β1，β2分别为首、末端局放信号相位常数；d为电缆局放源位置；l为电缆长度。

首、末端相位常数可利用式(13)分别计算得到。

(13)

式中：R0，G0，L0，C0分别为单位长度电缆电阻、电导、电感、电容值；ω在计算时为首、末端局放信号角频率分别取ω1,ω2。由于首、末端局放信号角频率有所差异，故相位常数会有所不同，将式(11)、式(12)作比可得式(14)。

(14)

式中：g(ω)=β1/β2，为首、末端局放信号相位常数比(以下简称为相位常数比)，最终PD位置估计可从d(ω)平均值获得。

综上所述，VMD-WVD相位法的具体步骤为：

(1) 在电缆首、末两端安装传感器，采集信号并对信号进行去噪提取并分割出首、末端局放信号。

(2) 根据式(9)将局放信号变换成频域信号。

(3) 将频域信号代入式(10)依次计算出首、末端局放脉冲相位谱。

(4) 对局放信号进行VMD-WVD处理得到信号波头时刻。

(5) 在相位谱中提取波头时刻和幅值时刻相位，代入式(14)以计算故障位置，局放故障位置可从d(ω)平均值获得。

2 VMD-WVD波头相位提取

2.1 现场局放信号提取

为验证VMD-WVD在实际工程中波头相位提取的精度，文中依托某供电公司电缆带电检测服务现场采集的局放信号进行验证。局放带电检测现场电缆型号YJV22-64/110 kV，电缆总长2 km。使用高频电流传感器环接在电缆屏蔽层接地线采集局放信号，其检测带宽能达30 MHz，采集系统采样率设置为200 MHz。局放信号经高频电流传感器采集后经50 Ω同轴电缆传输至采集系统，最后传输至电脑端进行处理。现场检测采集的2组信号如图1所示。

图1 现场采集的原始局放信号Fig.1 Original partial discharge signals collected on site

由图1可知受现场环境影响，局放信号埋没在大量噪声中。小波变换是最常用的信号去噪方法[22]，对图1的2组信号进行去噪分割局放脉冲后，局放信号分别如图2所示。

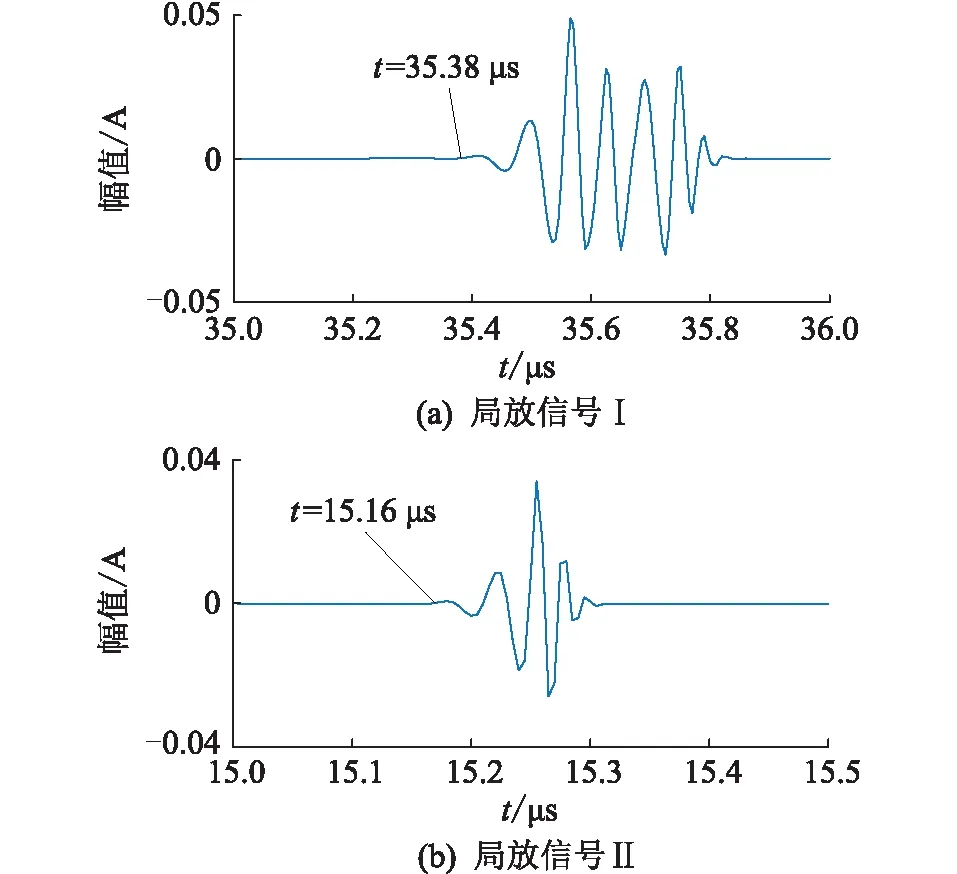
图2 局放信号波形Fig.2 Waveforms of partial discharge signals

2.2 现场局放信号波头相位分析

由于配网结构复杂，且受现场环境噪声等影响较大，局放信号波头检测较为困难[12]。由第1章分析可知，VMD-WVD能自适应地把局放信号分解成具有大量故障特征信息的IMF，可准确描述信号随时间的能量变化。通过检测局放信号突变点以确定局放信号波头时刻，使双端信号同步。对图2的2个局放信号进行VMD分解层数确定，具体结果如表1所示。

表1 能量差绝对变化率Table 1 Absolute change rate of energy difference

由表1可知，当k=8时，βa，βb分别出现最大值，故选取k=7作为最终分解层数，VMD-WVD分解结果如图3所示。

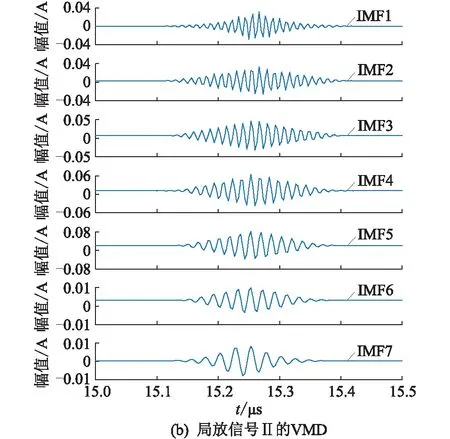
图3 局放信号的VMD结果Fig.3 VMD results of the partial discharge signals

图3将2组现场局放信号分解成不同频带的IMF，其中IMF1为高频分量。若直接使用IMF1来计算局放波头时刻较为困难[23]，通过对IMF1进行WVD，可得到局放信号的WVD瞬时能量分布，如图4所示。当电缆线路发生局放后，电缆局放瞬时能量可分为线路基频瞬时能量和局放后暂态瞬时能量[18]。其中基频瞬时能量相对平稳，暂态瞬时能量主要由分布式电缆模型中电感和电容放电产生，电感和电容放电是一个单调递减过程，因此局放信号波头时刻即为WVD瞬时能量分布幅值时刻。由图4可知，当电缆发生局放故障，最先到达两端的信号为局放入射信号，在局放信号到达前瞬时能量较为平稳；当局放信号到达后，在到达时刻附近产生一个尖峰，峰值时刻即为局放信号波头时刻。对比图2与图4可知，VMD-WVD能准确提取局放信号波头时刻。

图4 局放信号的WVD瞬时能量分布Fig.4 WVD instantaneous energy distribution of the partial discharge signals

3 VMD-WVD相位法影响因素分析

局放故障定位受故障位置、电缆长度及采样率等因素影响。如图5所示在PSCAD中搭建长电缆线路模型，进一步分析各因素对VMD-WVD相位法定位精度的影响。

图5 仿真模型Fig.5 Simulation model

文献[24]的研究内容以及图2的现场局放信号测量结果都表明，双指数振荡衰减脉冲能够很好地模拟实际局放信号，因此以式(15)对局放信号进行模拟。

(15)

式中：A为脉冲幅值常数，设为5 mA；τ为衰减常数，设为100 ns；fc为振荡频率，设为5 MHz。取fs为采样率，设为200 MHz。

文中采用交联聚乙烯电缆作为PSCAD电缆模型，电缆模型的结构示意如图6所示。该电缆相关参数为：交联聚乙烯电缆导体的半径R1为10.85 mm；交联聚乙烯电缆绝缘层的半径R2为17.15 mm；金属屏蔽层的半径R3为18.70 mm；外护套的半径R4为21 mm；主绝缘的介电常数为2.30；外绝缘的介电常数为5；缆芯和金属屏蔽层的电阻率皆为1.75×10-8Ω·m。

图6 电缆模型Fig.6 Cable model

图7为d=1 700 m时电缆首、末端采集的局放信号及其相位谱与WVD瞬时能量分布。

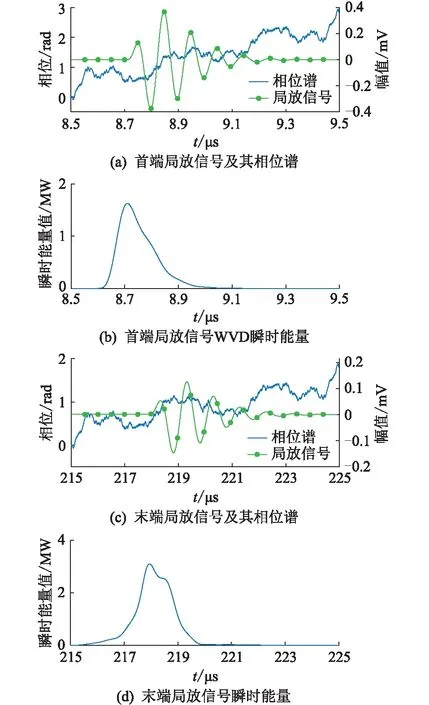
图7 首、末端局放信号和相位谱及WVD瞬时能量Fig.7 Partial discharge signals of the first-end terminal-end,phase spectrums and instantaneous energy of WVD

为验证波速，以100 m为步长，设置电缆长度l为1 500～3 000 m，记录不同长度下脉冲从末端到达首端的时刻，最终取平均值作为波速，经计算波速v=1.978 2×108m/s。参照文献[24]计算R0，L0，G0，C0，局放位置对定位精度影响如图8所示。

图8 不同局放位置的定位误差Fig.8 Positioning error of different fault distances

图9 不同电缆长度的定位误差Fig.9 Positioning error of different cable lengths

随着电缆长度增加，3种方法的定位误差呈增大趋势。VMD-WVD相位法平均定位误差为0.85%，长距离传播中波形色散影响导致相位误差，但平均误差小于1%，能够满足实际需求。

为了研究采样率对定位精度影响，改变采样率，设置l=5 km，d=l/2，定位误差如图10所示。

图10 不同采样率的定位误差Fig.10 Positioning error of different sampling rates

VMD-WVD相位法平均定位误差0.69%，在1 MHz采样率时定位误差达1.08%，但在100 MHz及以上时，误差保持0.5%左右。采样率降低，采样间隔增大，造成两端信号波头实际时刻与采样时刻的误差。故使用VMD-WVD相位法时，须采用高采样率。

4 结论

文中阐述了VMD-WVD的基本原理，在此基础上针对传统行波定位法在长电缆局放定位中时间同步和反射信号难识别的问题，提出一种基于VMD-WVD相位法的电缆局放故障双端定位，最终得出以下结论：

(1) 文中提出的VMD-WVD相位法不仅保留传统双端定位法只须采集入射局放信号的优点，且用相位代替波速，不必对波速进行验证。

(2) 经验证VMD-WVD相位法能准确提取局放入射信号波头时刻与相位，实现长电缆入射局放信号双端同步的优点，能够有效减小长电缆定位中时间难同步和反射局放信号难识别带来的影响。

(3) 文中所提的VMD-WVD相位法在故障位置、电缆长度、采样率3种影响因素下平均定位精度分别为0.54%，0.85%，0.69%，定位精度高于传统定位方法，采用100 MHz及以上采样率能获得更高的定位精度。