考虑数据不均衡的居民用户负荷曲线分类方法

张慧波， 王守相， 赵倩宇， 任杰， 王海

(1. 智能电网教育部重点实验室(天津大学)，天津 300072；2. 国网冀北张家口风光储输新能源有限公司，河北 张家口 075061)

0 引言

用户用电行为分析是电网分析规划的重要环节。随着智能采集装置的广泛应用，用户用电活动可通过智能电表采样并以负荷曲线等形式表现，其数据具有体量大、速度快、价值密度低等特征。针对用户负荷数据特点，研究高效的负荷曲线分类方法有助于电力公司从海量用电侧数据中挖掘用户潜在用电规律，对开展负荷预测、需求响应、电价决策等工作有着重要意义[1—2]。

目前，负荷曲线分类方法主要有无监督聚类、有监督分类以及无监督与有监督相结合等。近来年关于负荷曲线无监督聚类所做的研究主要集中于改进聚类算法[3—4]和改进聚类特征2个方面。在算法方面，文献[5]提出一种分段聚类方法对建筑负荷曲线分类，能够更高效地获取建筑的日典型用电模式。在聚类特征改进方面，主要聚焦在特征提取方法[6—8]和相似度度量计算方法[9—10]，文献[11]提出一种基于负荷曲线斜率分段的形状聚类方法，能够更好地捕捉曲线的形状特征；文献[12]采用样本皮尔逊相关系数距离作为相似度度量，算例表明优于欧几里得距离。在负荷有监督分类方面，应用最广泛的是反向传播神经网络(back propagation neural network，BPNN)[13—14]，但BPNN存在梯度爆炸、梯度消失等问题。在无监督与有监督结合方面，负荷数据作为无标签数据，利用无监督聚类获得类别标签，训练有监督学习模型进行分类，可将无监督与有监督的优势相结合，实现海量负荷数据的高效分类，其首先应获得训练集的精准类别标签[15—17]。

不均衡数据是指数据集中归属于某一类别的样本数量和密度与其他类别有较大差异。由于用户用电行为的随机性与多样性，负荷数据同样存在不均衡的现象，某些类别的负荷数量远少于其他类别的负荷数量。传统的K-means算法处理此类数据时容易出现“均匀效应”[18—19]，小类会吞噬大类中的部分样本，而传统分类方法同样在小样本类别上分类效果欠佳。目前在负荷曲线分类时考虑不均衡数据问题的研究较少，文献[20]改进密度峰值聚类(density peak clustering，DPC)算法实现了对多类别分布不均衡的负荷曲线聚类，但该算法计算复杂度较高，难以处理海量负荷数据；文献[21—23]利用过采样技术处理类别不平衡问题后训练分类模型，但其前提是训练集需要精准的类别标签，而负荷数据是无标签数据，难以获得准确的类别信息。

为了解决上述问题，提出一种无监督与有监督相结合的负荷曲线分类方法。首先，采用长短期记忆(long short-term memory，LSTM)神经网络自编码器对负荷曲线进行特征降维；然后，基于相对k近邻密度峰值(relatedk-nearest neigh￣bor density peaks，RKDP)初始聚类中心选取方法改进K-means获得训练集精准类别标签；最后训练搭建的LSTM-卷积神经网络(convolutional neural network，CNN)分类模型，实现大规模负荷数据分类。

1 RKDP初始聚类中心选取方法

DPC算法的核心思想为：聚类中心本身的局部密度大，即其被小于其密度的邻居所包围；聚类中心与其他具有更大密度的数据点之间有相对大的距离[24]。在DPC算法中，每个数据点i有2个重要参数：局部密度ρi与相对距离δi。

基于高斯核计算数据点i的局部密度ρi为：

(1)

式中：di,j为数据点i,j之间的距离；dc为截断距离，即距离阈值。与数据点i距离小于dc的点越多，该点的局部密度ρi就越大。

相对距离δi为数据点i与其他密度比它大的数据点的所有距离中的最小值，计算公式为：

(2)

根据DPC算法的核心思想，将相对距离大且局部密度值大的点选定为聚类中心，然后将剩余数据分配到密度比它高的最近数据点所在类别，快速完成聚类。然而，DPC算法在数据集密集程度不均时效果较差，这是由于该算法定义的局部密度是由全局数据进行计算，未考虑数据内部局部结构差异。当数据集不同类别间密集程度差异较大时，全局范围内密度较高的点可能全分布在密集类别中，容易忽略密度稀疏的类别，难以找到正确的初始聚类中心[25]。因此，通过计算数据点与其近邻点间相对密度可能更能反映该点是否为潜在的聚类中心。

文中基于DPC算法思想，提出RKDP初始聚类中心选取方法，该方法须提前设定2个参数：聚类中心数K和k近邻的参数n，其具体流程如下。

(1) 首先，通过数据点i与其近邻点的距离来计算其局部密度，新的局部密度ρi计算公式如式(3)所示，Ni为i的n个近邻点集合。

(3)

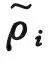
(4)

(3) 基于DPC算法思想(聚类中心有着较大的局部密度与相对距离)引入聚类中心权值γi来选择初始聚类中心，计算公式如下：

(5)

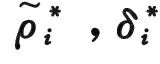
2 LSTM自编码器

自编码器(auto-encoder，AE)是一种常用于特征提取与降维的神经网络，包括编码与解码2个过程，其基本结构如图1所示，包括输入层、隐藏层和输出层3个部分[8]。AE的思想就是在输出层最大程度重构输入数据，同时通过隐藏层提取输入数据的隐藏特征，通过设置隐藏层神经元数量小于输入数据维度即可实现特征降维。

LSTM神经网络是一种改进的时间循环网络，依靠其独特的门控结构和记忆单元可有效处理长时间序列，目前在时序预测、分类等领域有广泛的应用。LSTM神经网络基本单元主要包括遗忘门、输入门和输出门3个门控单元[23—24]。

图1 AE结构Fig.1 Structure of AE

文中将传统AE与LSTM神经网络相结合，提取负荷数据的时序特征，所提出的LSTM-AE网络结构如表1所示。

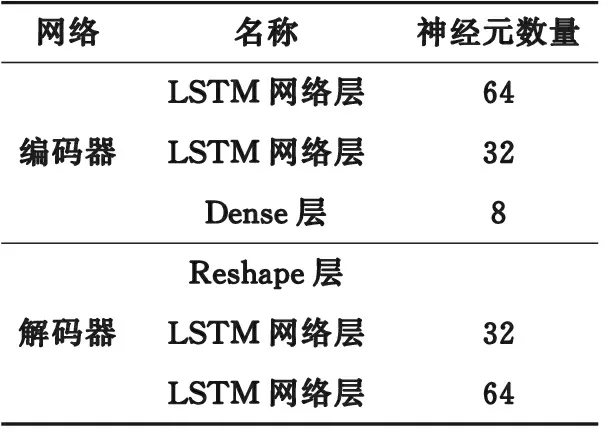
表1 LSTM-AE网络结构Table 1 Network structure of LSTM-AE

3 基于LSTM-CNN的负荷曲线分类模型

CNN近年来在深度学习领域被广泛应用，其内部基于局部连接和共享权值的方式可有效提取数据的潜在特征[26—27]。文中使用CNN提取负荷数据的深层次特征，同时与LSTM神经网络提取的时序特征拼接作为特征向量，实现特征增强，从而提升分类模型对不平衡数据的处理能力。所提出的LSTM-CNN分类模型如图2所示，主要包括CNN子模块、LSTM子模块以及分类模块。CNN子模块主要由2层的一维卷积层与池化层组成。Reshape层转换输入数据维度，2层卷积层提取数据特征，激活函数为Relu；池化层对卷积层提取特征进行下采样，实现特征约简。LSTM子模块由2层LSTM网络层构成，神经元数量均为64，激活函数为Relu，用于提取负荷的内在时序特征。分类模块中，特征拼接层对LSTM及CNN子模块提取的特征进行拼接，输出为一维特征向量；第一层全连接层实现特征降维，激活函数为Relu，数量为32；第二层全连接层激活函数设置为Softmax，其神经元数量取决于负荷类别数，输出最后的分类结果。

图2 LSTM-CNN分类模型结构Fig.2 Structure of LSTM-CNN classification model

4 算例分析

4.1 实验数据及评价指标

4.1.1 实验数据介绍

由于负荷数据缺乏类别标签，无法直接测试所提方法对不均衡数据的分类能力，文中基于UCI数据集中的DIris，DWine，DSeed数据集来验证RKDP初始聚类中心选取方法的有效性，同时选取Synthetic Control时序数据集对所提出的LSTM-CNN分类模型进行测试。最后，选取伦敦智能电表数据集DL及爱尔兰负荷数据DI作为实际负荷数据进行负荷聚类及分类实验(采样时间间隔均为30 min，即每天有48个采样点)，验证所提方法的有效性。文中所使用的实验平台处理器型号为AMD Ryzen Threadripper 3970X，操作系统为Windows 10，所用编程语言为Python 3.7，所提出的神经网络模型采用keras深度学习框架搭建。

4.1.2 评价指标介绍

在聚类性能评估指标方面，对于有类别标签的数据集，选取调整互信息(adjusted mutual in￣for￣ma￣tion，AMI)iAMI、调整兰德系数(adjusted rand in￣dex，ARI)iARI和Fowlkes-Mallows指数(fowlkes-mal￣lows index，FMI)iFMI3项指标来描述聚类结果与实际标签的吻合程度，上限均为1，其值越接近1表示聚类效果越好。对于无标签负荷数据，选取常用的轮廓系数(silhouette coefficient，SC)iSC和戴维森堡丁指数(Davies-Bouldin index，DBI)iDBI，iSC值越大、iDBI越小意味着类内距离越小，类间距离越大，聚类效果越好[28—30]。在分类模型评估指标方面，直接选择分类准确率作为分类模型的评价指标。

4.2 RKDP-K-means性能测试

4.2.1 RKDP有效性验证

首先将RKDP-K-means算法直接与K-means算法进行对比，验证RKDP初始聚类中心选取方法能够提升K-means方法对不均衡数据的聚类精度。基于DIris，DWine，DSeed3个真实数据集，采用随机抽样法分别构建不平衡比例为3∶1，5∶1，10∶1的数据集，聚类数均为各数据集的类别数，k近邻参数在3～20之间选取，每种不平衡比例下重复5次，即每个数据集进行15次实验，2种方法的iARI，iAMI，iFMI及其平均值分别见表2和表3，iIter为迭代次数均值。

由表2和表3可知，K-means算法聚类精度随着不平衡比例加重逐渐下降，以DWine数据集为例，数据不平衡比例由3∶1变为10∶1时，iARI指标由0.858变为0.670，而RKDP-K-means算法由0.876变为0.804，仍保持较高水平；在各指标平均值方面，相对于K-means算法，RKDP-K-means算法的iARI，iAMI，iFMI均有提升，且迭代次数减少。综上，文中所提出的RKDP初始聚类中心选取方法能够有效提升K-means算法对不平衡数据的处理能力。

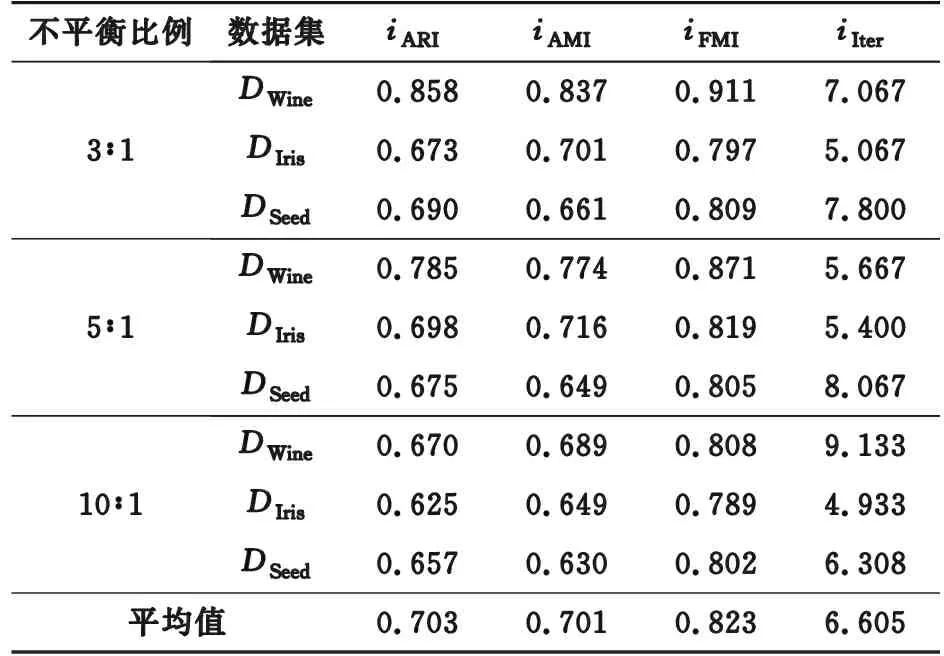
表2 K-means实验结果Table 2 Experimental results of K-means

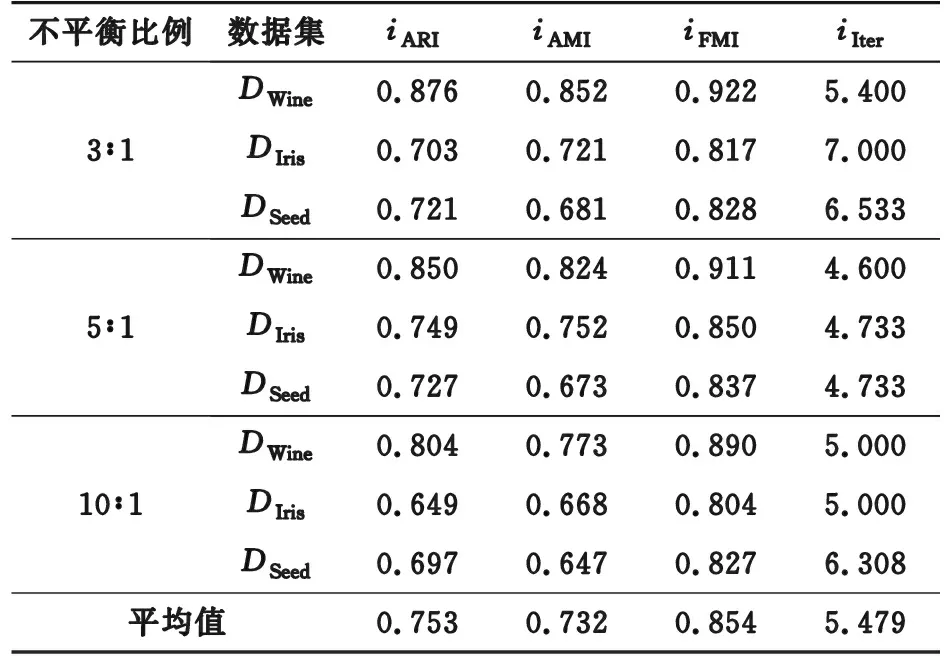
表3 RKDP-K-means实验结果Table 3 Experimental results of the RKDP-K-means

4.2.2 聚类效果对比分析

为了更加客观地验证所提算法处理不均衡数据的有效性，将RKDP-K-means算法与基于划分的K-means、基于空间密度的聚类(density-based spatial clustering of applications with noise，DBSCAN)[31]、基于层次的凝聚聚类(agglomerative clustering，AG)及基于图论的谱聚类(spectral clustering，SP)4种方法进行对比。其中，K-means、AG及SP聚类数设置为3，DBSCAN邻域半径以0.02为步长，在0.1～0.5之间选取，邻域内最少样本数在5～25之间选取，RKDP-K-means的k近邻参数在3～20之间选取。所有结果均为最佳参数下测得，每组不平衡数据同样重复5次，表4为5种方法的准确率。

由表4可知，RKDP-K-means算法在各数据集下均优于K-means算法，以DWine数据集为例，随着不平衡比例加大，K-means的准确率从0.957变为0.829，RKDP-K-means从0.964变为0.915，仍有较高准确度。整体上看，RKDP-K-means算法的准确率均值均优于其他4种方法。因此，RKDP-K-means算法在处理不平衡数据时具有优势。

表4 5种聚类算法准确率Table 4 Accuracy of five clustering algorithms

4.3 实际负荷数据聚类分析

采用实际负荷数据来对LSTM-AE的性能进行评价分析。从DL数据集中随机选取500条负荷曲线为实验对象，基于K-means算法计算不同聚类数下的iSC，iDBI指标，结果如图3所示，当聚类数目为4时，2项指标所反映的聚类效果较好，因此设置聚类数为4。分别采用LSTM-AE、主成分分析(prin￣cipal component analysis,PCA)、核主成分分析(kernel PCA，KPCA)、AE 4种降维方法(维度均设置为8)降维后采用RKDP-K-means聚类以及K-means，RKDP-K-means不降维直接聚类进行对比，重复10次试验。同时基于DI重复上述实验进行验证，聚类中心数设置为3，结果如表5所示。

图3 SC和DBI与聚类数目关系Fig.3 Relationship between SC,DBI and cluster number

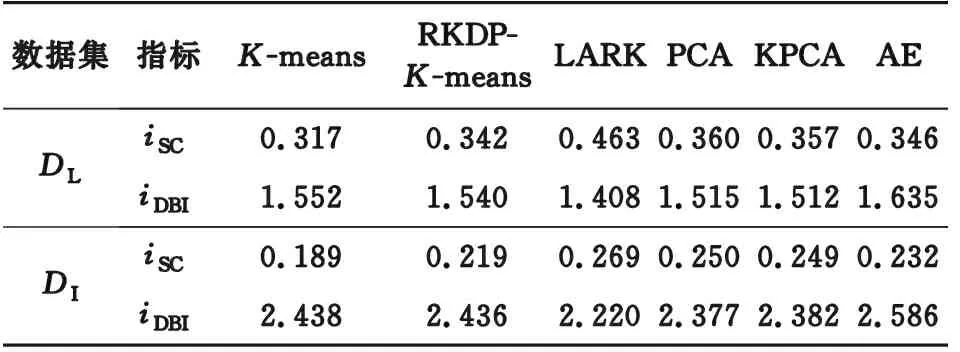
表5 LSTM-AE有效性验证实验结果Table 5 Results of validity verification of LSTM-AE

为表述方便，将经LSTM-AE降维后RKDP-K-means聚类命名为LARK聚类算法。由表5可知，RKDP-K-means在iSC指标上优于K-means算法，iDBI指标基本持平。与RKDP-K-means聚类相比，LARK算法的各项指标均有较大幅度的改善，在DL和DI数据集上，iSC指标分别提升0.121和0.05，这表明LSTM-AE能够提升RKDP-K-means的聚类精度。通过对比4种降维方法可以发现，LSTM-AE的特征提取能力优于其他3种方法。

4.4 LSTM-CNN分类模型测试

4.4.1 LSTM-CNN网络测试

首先，使用Synthetic Control时序数据集测试所提出的LSTM-CNN分类模型，与相同结构的LSTM网络模型以及传统支持向量机(support vector machine，SVM)模型进行对比，训练集与测试集比例为1∶1，神经网络迭代次数设置为100，优化器为adam，损失函数为MSE；SVM算法中核参数为径向基，分类准确率如表6所示。由表6可知，3种方法在训练集上均有100%的准确率，在测试集上，LSTM模型最弱，仅有95.3%，而所提出的LSTM-CNN分类模型与SVM均达到了97.7%的准确率。

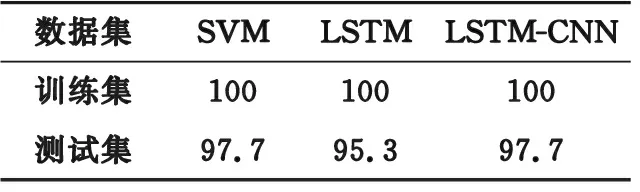
表6 3种方法分类准确率对比Table 6 Classification accuracy comparisonof three methods %

为了验证LSTM-CNN模型对不平衡时序数据的分类性能，基于Synthetic Control时序数据集构建了15种类别不平衡数据集，与LSTM模型和SVM模型进行对比，传统SVM模型处理不平衡时序数据性能较弱，准确率均值仅有80.7%，LSTM模型准确率均值为87.9%，而所提LSTM-CNN模型相对其他2种方法有着更好的分类性能，准确率高达92.2%。由此可见，提出的基于LSTM-CNN模型能够有效处理时序不平衡数据分类问题。

4.4.2 实际负荷数据分类测试

(1) 算法分类性能测试。基于DL和DI负荷数据，分别随机选取10万条负荷曲线，按照3∶7构造训练集与测试集，基于LARK获得训练集标签数据，训练LSTM-CNN模型实现对测试集的分类，与K-means和LARK直接聚类进行对比，DL，DI的聚类中心数分别设为6和8，iSC和iDBI指标如表7所示。由表7可知，文中方法聚类精度优于LARK算法，在2个数据集上，iSC指标分别提升0.043和0.044。K-means算法虽然在DI上iDBI指标最小，但其iSC指标仅有0.074，文中方法iSC指标相较于K-means提升0.118，iDBI指标提升0.172，整体上看，所提出的分类方法分类性能优于其他2种方法。

表7 3种方法SC、DBI对比Table 7 Comparison of SC,DBI of three methods

(2) 负荷分类结果。图4为基于DI归一化后的负荷分类结果，可以看出用户的用电模式多种多样，8种典型负荷曲线可大致分为平稳型用电和尖峰型用电。类别1一整天始终保持较高的负荷水平，在凌晨用电量较大。类别5也是平稳型用电类型，但其负荷水平一直很低。其余6种皆为尖峰型用电，但用电高峰时段不同，类别7是典型的午间负荷，类别4和类别6用电高峰分别出现在下午和傍晚，类别2、类别3和类别8是典型的晚间负荷，其中类别3的用电高峰时间持续较长。通过挖掘用户的典型用电模式，有助于电力公司制定更好的售电方案，提高服务水平。

图4 典型负荷曲线Fig.4 Typical daily load profiles

(3) 算法效率测试。文中所提方法包括LARK聚类获取样本标签、LSTM-CNN模型训练及分类3个环节，实验对比了K-means、LARK及文中方法(训练集∶ 测试集=3∶7)在不同规模负荷数据集下的计算速度，执行时间如图5所示。

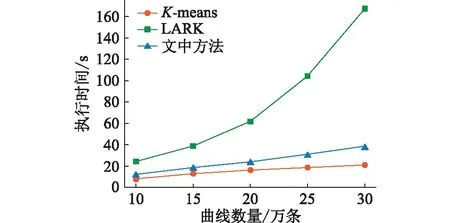
图5 算法效率对比Fig.5 Comparison of algorithmic efficiency

从图5可以看出，LARK聚类算法随着数据规模增加运行时间急剧增大，在对30万条负荷曲线分类时，LARK算法运行时间达到167 s，而文中方法仅用时37.4 s，相比于LARK算法效率提升3.46倍；传统K-means算法用时20.5 s，文中方法虽相较于K-means算法较差，但在分类性能上表现更好，同时文中方法主要耗时在于标签获取与训练分类模型环节(共耗时34.2 s)，分类阶段用时仅3.22 s，分类模型一旦训练完成后可重复使用。因此，文中所提方法在面对大规模负荷分类时具有效率优势。

5 结论

文中提出了一种考虑数据分布不均衡的负荷曲线分类方法，主要包括基于LSTM-AE实现负荷数据降维、基于RKDP-K-means聚类算法获得负荷类别标签及训练LSTM-CNN分类模型实现大规模负荷分类三部分。通过算例分析验证了文中方法的有效性，得到以下结论：

(1) 基于UCI公共数据集验证了所提出的RKDP初始聚类中心选取方法可有效提升K-means算法对不均衡数据的聚类性能，其中iARI指标提升6.6%，迭代次数减少17.1%；

(2) 在RKDP-K-means算法对负荷进行聚类分析时，所提出的LSTM-AE特征提取方法可有效提升RKDP-K-means的聚类精度，在伦敦负荷测试集，iSC指标提升35.4%；

(3) 在大规模负荷分类上，基于LARK聚类与LSTM-CNN分类模型相结合的负荷分类方法相比于LARK算法有着更好的负荷分类性能，其中iSC指标提升29.7%，效率提升3.46倍。