风速对基于BOTDA架空导线覆冰监测有效性的影响

徐志钮， 李先锋， 郭一帆， 赵丽娟

(华北电力大学电气与电子工程学院，河北 保定 071003)

0 引言

输电线路覆冰易导致输电线路的机械和电气性能急剧下降[1]，不仅造成巨大的经济损失[2]，还严重影响电力系统的安全稳定运行[3]。监测输电线路的运行状态以估计覆冰所造成的威胁，及时采取相应的措施以抑制覆冰造成的危害显得尤为重要[4]。同时输电线路覆冰监测和预警还为线路防冰和除冰提供必要的决策支持[5]，具有重要价值。

传统的输电线路覆冰监测一般分为称重法[6—7]、图像法[8—9]、导线倾角法[6,10—11]、模拟导线法[8,12—13]等，这几种监测方法各有特色，能节约人力物力，可以降低成本和保障系统的安全稳定运行。但上述的几种方法有一定的局限性，如容易受环境的影响、使用寿命较短、数据传输可靠性差、无法准确全面地监测输电线路的状态等[6,8,11,13]。为此学者不断研究可以提高覆冰监测系统性能的措施，不断提高监测设备精度和测量距离。分布式光纤传感技术具有较好的电绝缘性，很强的抗电磁干扰能力和较高灵敏度，同时理论上能监测线路全长，非常适合在输电线路的高电压、强电磁干扰、强腐蚀等恶劣环境下工作，且较其他方法而言更能保障测量数据的精确度及监测系统工作的稳定性[14]。于是，分布式光纤传感技术在电力行业中的应用逐渐成为国内外学者研究的热点。华北电力大学李成宾等人分析了将分布式光纤传感技术应用到输电线路覆冰在线监测中的可能性[15]；李永倩等人利用布里渊光时域分析(Brillouin optical time domain analysis,BOTDA)传感系统对某电力公司的全介质自承式(all-dielectric self-supporting,ADSS)光缆进行了实地监测[16]，实现了对16 km的ADSS光缆温度/应变的在线监测，指出了BOTDA传感技术在输电线路监测方面有着很好的应用前景；覃兆宇等人所设计基于布里渊光时域反射(Brillouin optical time domain reflectometer,BOTDR)技术的覆冰识别系统在昭通成功实现了75 km长光纤架空地线(optical fiber composite overhead ground wire,OPGW)的实地监测[17]，所设计的系统温度精度达到了±2 ℃，实验效果较好，系统所监测出来的覆冰情况与巡线人员观察的覆冰情况一致；吴念等人也利用BOTDR技术实现了对OPGW导线的监测，并且在覆冰实验基地实验证实了温度监测可以对线路覆冰的情况进行有效识别，且监测结果与人工观测结果一致[18]。这些研究表明利用分布式光纤传感技术实现输电线路覆冰监测的可行性、有效性与准确性。文献[17—18]均验证了架空导线在覆冰后导线温度变化会滞后于环境温度变化结论的正确性。在实际运行中，风速是影响架空导线温度的重要因素之一，风速对覆冰后的架空导线温度变化是不能忽略的[19]，在文献[17—18]的监测过程中均存在不足，文献[17]在建模仿真时涉及到的风速只有1 m/s一个值，并没有明显地体现出风速对覆冰的架空导线温度变化的影响；文献[18]在建模仿真时并没有指出涉及到风速这种因素，也未说明风速对架空导线温度的影响。综上所述，现有研究并没有涉及架空导线温度变化与环境温度、风速和覆冰厚度等因素之间的关系研究以及结论，也未涉及环境温度对基于分布式光纤传感输电线路覆冰监测有效性的影响，更未提及常见范围环境温度和覆冰厚度下的临界风速。

为了解决上述存在的问题，文中利用COMSOL Multiphysics 5.4有限元软件仿真建立了光纤复合相线(optical phase conductor,OPPC)的覆冰模型，模拟改变模型所处的环境温度等气象条件以及覆冰厚度和长度等条件，分别进行了温度场是否包含焦耳热2种情况下的计算。文中分析总结了OPPC架空导线覆冰段与未覆冰段的光纤温度在不同气象条件下的变化特征；指出可以根据一段时间内的光纤温度变化有效判断出是否覆冰；光纤温差作为覆冰判据，着重探究了临界风速与环境温度和覆冰厚度之间的关系；给出了临界风速与环境温度之间的拟合公式和临界风速与架空导线覆冰厚度之间的拟合公式；得到了常见范围的温度变化率和覆冰厚度下的临界风速值，指出根据现有数据利用插值方法求得所需的临界风速，可用于判断现实情况中分布式光纤温度传感方法是否可用于架空导线覆冰监测。

1 线路覆冰识别理论

OPPC架空导线温度变化是多种因素耦合造成的，不同时间段以及不同季节和不同的架空导线结构都是引起温度变化的原因。架空导线温度主要随着外界环境温度的变化而变化，导线吸收和损失热量使导线达到一种热平衡状态。反之，导线温度也可反映环境温度变化。例如，冬季寒冷季节架空导线是否覆冰可根据架空导线温度的变化来判断。OPPC是一种新型的电力专用光缆，具有电能传输和光信号传输的作用[20]。OPPC导线的设计结构、材质以及运行条件都会影响架空导线的温度。太阳辐射Qsun、对流散热Qcon、辐射散热Qrad和焦耳热QJoul是引起线路温度变化的主要因素，其表达式如式(1)—式(4)所示[17]，其满足热平衡方程[21]，如式(5)所示。

Qsun=αJdOPPC

(1)

(2)

Qrad=πdOPPCεσ[(T+273)4-(Tamb+273)4]

(3)

QJoul=I2Rt

(4)

Qsun+QJoul=Qcon+Qrad

(5)

式中：α为吸热系数；J太阳辐射率；dOPPC为OPPC架空导线直径；λ为对流散热系数；T为架空导线温度；Tamb为环境温度；LRe为雷诺数；ε为辐射系数；σ为玻尔兹曼常数；I为电流有效值；R为架空导线电阻；t为时间。

架空导线覆冰后，太阳辐射Qsun-ice、辐射散热Qrad-ice会发生变化，如式(6)和式(7)所示[17—18]。在不考虑融冰对架空导线温度影响的情况下，研究架空导线在不同环境温度和不同覆冰厚度情况下温度随时间的变化情况。文中采用瞬态热传导方程进行研究，考虑焦耳热对计算的影响，架空导线覆冰时如式(8)所示[17]，架空导线未覆冰时如式(9)所示[17]。

Qsun-ice=αJ(dOPPC+2b)

(6)

Qrad-ice=π(dOPPC+2b)εσ×
[(T+273)4-(Tamb+273)4]

(7)

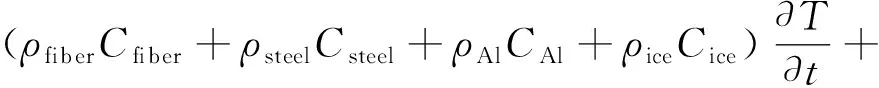
(8)

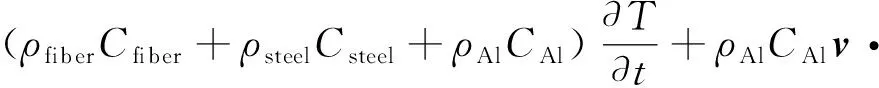
(9)

式中：ρfiber，ρsteel，ρAl，ρice分别为光纤、钢、铝和冰的密度；Cfiber，Csteel，CAl，Cice分别为光纤、钢、铝和冰的比热容；b为覆冰厚度；v为风速；ksteel，kfiber，kAl，kice分别为钢、光纤、铝、冰的导热系数。

文献[22]指出影响架空导线温度的因素主要与架空导线所处环境的气象条件有关，若不考虑焦耳热对计算的影响，则架空导线覆冰时温度如式(10)所示[17]，架空导线未覆冰时如式(11)所示[17]。

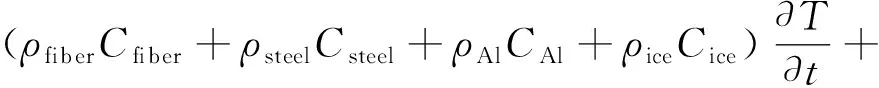
(10)

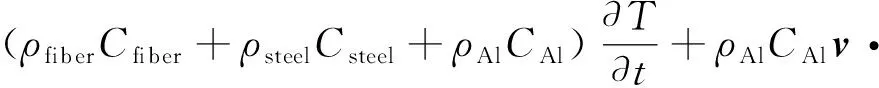
(11)

通过观察式(8)—式(11)可知，除了太阳辐射、对流散热和辐射散热因素会引起架空导线温度变化外，在瞬态研究过程中引起覆冰段与未覆冰段光纤温度变化的原因还有：(1) 架空导线的比热容与冰的比热容不同，外界温度变化一定的情况下，覆冰段光纤所得到的热量要小于未覆冰段，温度变化较小；(2) 架空导线材料的密度和冰的密度也会影响架空导线温度变化；(3) 线路所处的气象环境如风速和环境温度都是引起线路覆冰段与未覆冰段温度不同的因素。

2 线路覆冰光纤温度场模型建立

架空导线覆冰的温度场涉及到环境与架空导线之间的热量传递和架空导线各结构之间的热量传递，第2章采用考虑焦耳热的温度场进行计算，在第3—6章采用不考虑焦耳热的温度场进行计算。在研究架空导线覆冰温度分布情况过程中，热源主要为架空导线流经电流所产生的焦耳热和环境对架空导线辐照所产生的热量。热量传递主要有架空导线各部分以及冰层之间的热传导，架空导线各部分以及冰层对环境的热辐射和对流散热。文中采用COMSOL Multiphysics 5.4有限元仿真软件对OPPC覆冰与未覆冰状态下的架空导线中的光纤温度变化进行研究。文中模型仿真的OPPC光缆型号为OPPC-24B1-240/30，如图1(a)所示。实际考虑到计算机性能，为提高计算效率，对OPPC架空导线进行以下简化[23]：

(1) OPPC为层绞式[24]，忽略内部的填充油膏；

(2) OPPC内部的24芯光纤等效为1根；

(3) 不计内部钢芯铝线层之间和钢芯与光纤之间的距离；

(4) 假设材料为各向同性，并且将6根钢芯等效为1根嵌套光纤的钢芯，24根铝线等效为1根套筒状的铝线；

(5) OPPC各部分的传热系数不会随着温度的改变而改变。

OPPC简化前的物理模型横截面如图1(b)所示，经过简化后的物理模型截面如图1(c)所示。

图1 OPPC物理模型简化示意Fig.1 Physical model simplified schematic diagram of OPPC

在仿真架空导线覆冰时，建立OPPC架空导线覆冰的三维模型。假设此模型中OPPC长5 m，分为5段各1 m，假设第2段和第4段覆冰，为便于计算，设冰层均匀覆盖线路，其余3段则未覆冰[17—18]，如图2所示，仿真计算过程中各结构参数和材料属性如表1中所示。

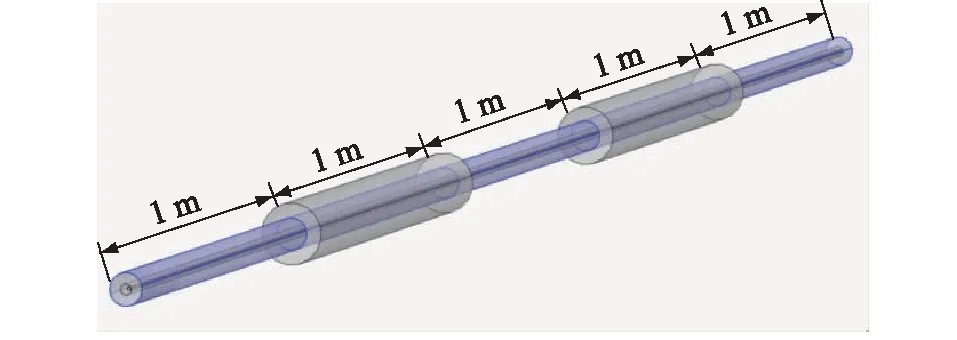
图2 物理模型示意Fig.2 Schematic diagram of physical model

表1 仿真参数Table 1 The simulation parameters

文中为兼顾计算效率以及结果精确度，仿真计算前对所建立的物理模型进行网格划分，采用了自由四面体网格进行剖分。网格密度方面，理论上网格密度越大，计算值与理论结果越接近。但是该方式易产生求解时不收敛的问题，同时还会减缓计算的速度，故文中选择最为合适的网格密度，既保证了求解时的收敛性，又保证了计算结果合理正确，图3为具体的网格划分结果示意图。模型中四面体网格有27 259个，求解器计算的时间初始值为0 h，步长为0.5 h，仿真时长共5 h。

图3 网格划分示意Fig.3 Schematic diagram of meshing

采用温度场进行瞬态研究，所设定的气象环境参数：风速为0 m/s；冰层均匀覆盖线路时，冰层厚度为10 mm；长度为1 m；温度上升阶段的环境初始温度为-7.5 ℃；下降阶段的环境初始温度为0 ℃；太阳辐照度为200 W/m2[17]。仿真实验中设置的仿真时间为5 h，环境温度以1.5 ℃/h下降或上升，每0.5 h绘制一次光纤内部的温度分布曲线，仿真结果如图4和图5所示，图中横轴表示光纤长度，纵轴表示光纤上的温度，每条曲线表示某时间点光纤的温度分布。

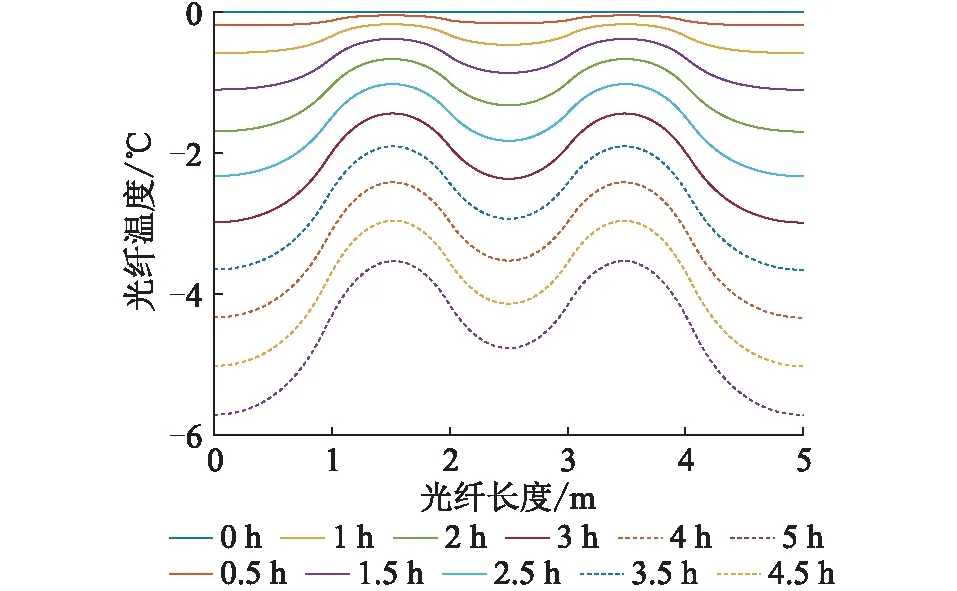
图4 光纤沿线温度,环境温度以1.5 ℃/h下降Fig.4 The temperature along the fiber under the ambient temperature dropping by 1.5 ℃/h

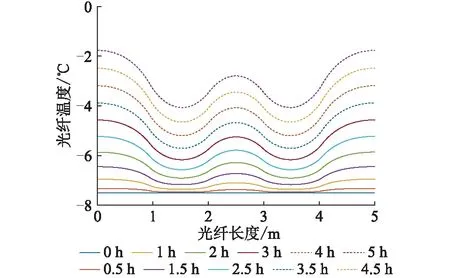
图5 光纤沿线温度,环境温度以1.5 ℃/h上升Fig.5 The temperature along the fiber the under ambient temperature rising by 1.5 ℃/h

当环境温度以1.5 ℃/h下降时，由图4中的5 h温度分布曲线可知覆冰段温度下降3.5 ℃，未覆冰段温度下降5.7 ℃，温差为2.2 ℃。在环境温度下降时，覆冰段温度下降的幅度要小于未覆冰段的幅度。同理，分析图5可知在环境温度上升时覆冰段温度上升的幅度要小于未覆冰段的幅度，这与实际现象相符，同时与文献[17—18]中的结论也基本一致，证实了文中仿真的正确性。

OPPC中电流流过所产生的焦耳热也是影响架空导线温度的重要因素之一，因此仿真中该覆冰模型考虑焦耳热的温度场进行计算，根据OPPC的设计参数，通入大小为552 A的电流，其余的气象条件都不变。由于实验仿真温度上升和下降时的温度变化结果具有一定的相似性，因此只考虑环境温度在下降时的光纤温度变化情况，定义光纤温差为光纤温度的最大值减去光纤温度的最小值，实验结果如图6和图7所示。

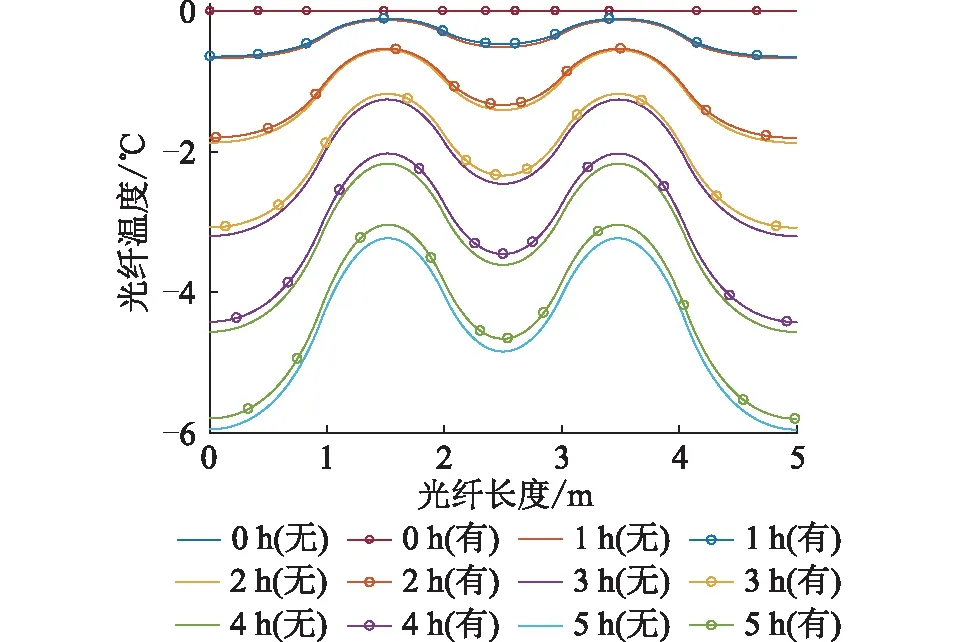
图6 有无焦耳热时的光纤温度Fig.6 Temperature of the fiber with or without Joule heat

图7 有无焦耳热时的光纤温差Fig.7 Temperature difference of the fiber with or without Joule heat

由图6可知，针对导线运行5 h后的光纤温度变化情况，是否考虑焦耳热对仿真结果影响较小，二者之间仅相差0.09 ℃。文中判断架空导线是否覆冰的依据是光纤温差，结合图7可知有无焦耳热对温差曲线趋势基本无影响，且2条曲线基本重合，5 h后2条曲线的温差值为0.04 ℃，焦耳热对温差研究结果的影响可忽略，故文中第3—6章研究内容基于不考虑焦耳热的OPPC架空导线覆冰模型。

3 光纤温度与风速的关系

对流散热和辐射散热主要与线路所处环境的风速、温度、覆冰厚度和覆冰长度等因素有关，研究时暂先考虑环境温度下降时的光纤温度变化。设环境初始温度为0 ℃，环境温度以1.5 ℃/h下降，覆冰的厚度10 mm，覆冰长度1 m，风速分别为0 m/s，1 m/s，5 m/s，9 m/s，15 m/s进行研究，仿真5 h后得到不同风速条件下的架空导线覆冰段与未覆冰段随时间变化的光纤温度曲线，如图8和图9所示。取覆冰段光纤的中间点温度作为光纤覆冰段温度；架空导线0 m位置处是架空导线温度最低的点之一，选取该点温度作为未覆冰段的光纤温度。图8和图9中所指的覆冰段和未覆冰段温度分别为这2点的温度。

图8 不同风速时未覆冰段光纤温度Fig.8 The temperature of the fiber in the OPPC without ice cover at different wind speeds

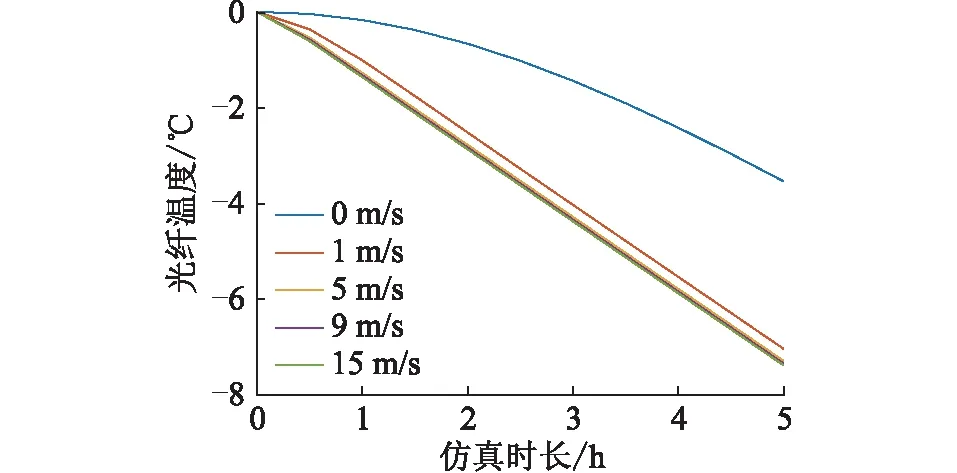
图9 不同风速时覆冰段光纤温度Fig.9 The temperature of the fiber in the ice-coated OPPC at different wind speeds

由图8和图9可知，当风速大于等于1 m/s时，0.5 h之后，未覆冰段和覆冰段的光纤温度下降速率基本上等于环境温度的下降速率，这是因为冰层厚度为10 mm，长度为1 m，覆冰量相对较少导致冰减缓覆冰段光纤温度下降的程度较小，且风速相对较大，使得架空导线温度迅速与环境温度之间形成动态平衡。同理，未覆冰段的架空导线本身的比热容相对小，易快速达到一种平衡状态。在风速大于1 m/s时，覆冰段与未覆冰段的光纤温度的下降速度与环境保持一致。

由上述的结果可知，风速大于1 m/s时其对光纤温度的影响较大，又考虑到所设置的风速大小的步长间距较大，因此难以得到风速在0～1 m/s情况下光纤温度的变化情况。为研究光纤温度与风速之间的关系，文中细化0～1 m/s区间的风速值步长，风速值取0 m/s，0.025 m/s，0.05 m/s，0.075 m/s，0.1 m/s，0.15 m/s，0.2 m/s，0.4 m/s，0.6 m/s，0.8 m/s，1 m/s，其余条件不变，继续仿真光纤温度。未覆冰段温度如图10所示，覆冰段温度如图11所示，覆冰段与未覆冰段的温差如图12所示。

图10 风速0～1 m/s时未覆冰段光纤温度Fig.10 The temperature of the fiber in the OPPC without ice cover at wind speeds of 0 to 1 m/s

图11 风速0～1 m/s时覆冰段光纤温度Fig.11 The temperature of the fiber in the ice-coated OPPC at wind speeds of 0 to 1 m/s

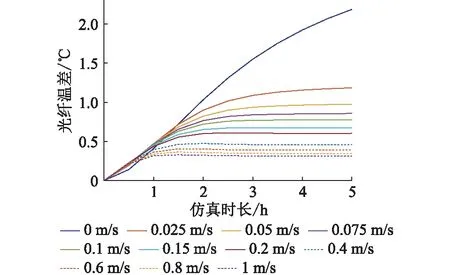
图12 风速0～1 m/s时光纤温差Fig.12 The temperature difference of the fiberin OPPC at wind speeds of 0 to 1 m/s

由图12可知，当风速值大于0.2 m/s时，覆冰段与未覆冰段的温差在2 h之后就基本保持稳定；风速值大于0.05 m/s，温差在3 h之后基本上保持稳定；风速为0.025 m/s和0.05 m/s时，3 h—5 h虽然温差值在增大，但是增幅较小；风速值为0 m/s时，温差持续增加，幅度也较大，5 h后的温差达到了2.2 ℃。由图8—图12可知，风速为0 m/s的温差曲线与风速不为0 m/s的情况差异明显，这说明在此环境条件下，风速对架空导线的温度影响显著，温差对风速敏感。

架空导线的吸热与散热是一个积累且渐变的动态热平衡过程，风速的存在加快了架空导线达到热平衡状态的速度。此外，其他影响因素如环境温度也易影响架空导线达到热平衡状态的过程，这也是风速低但会很快达到热平衡的原因。

4 光纤温度与环境温度的关系

在第3章中提到环境温度也是影响架空导线热平衡的因素，因此第4章主要研究架空导线温度与环境温度之间的关系。环境温度对架空导线温度的影响与环境温度初始值和环境温度变化率有关，文中将分别对这2个影响因素进行研究。

4.1 光纤温度与环境温度初始值的关系

设环境温度以1.5 ℃/h下降，架空导线覆冰厚度为10 mm，覆冰长度为1 m，风速为0 m/s，选择不同的环境温度初始值(0 ℃，-1 ℃，-2 ℃，-3 ℃，-4 ℃)进行仿真，仿真5 h后得到不同环境温度初始值情况下的覆冰段架空导线光纤温度随时间变化曲线、未覆冰段架空导线光纤温度随时间变化曲线和架空导线光纤温差随时间变化曲线，如图13—图15所示。

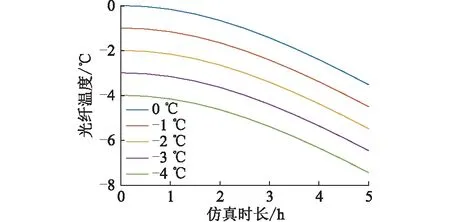
图13 不同初始环境温度时的覆冰段光纤温度Fig.13 The temperature of the fiber in the ice-coated OPPC with different initial values of ambient temperature

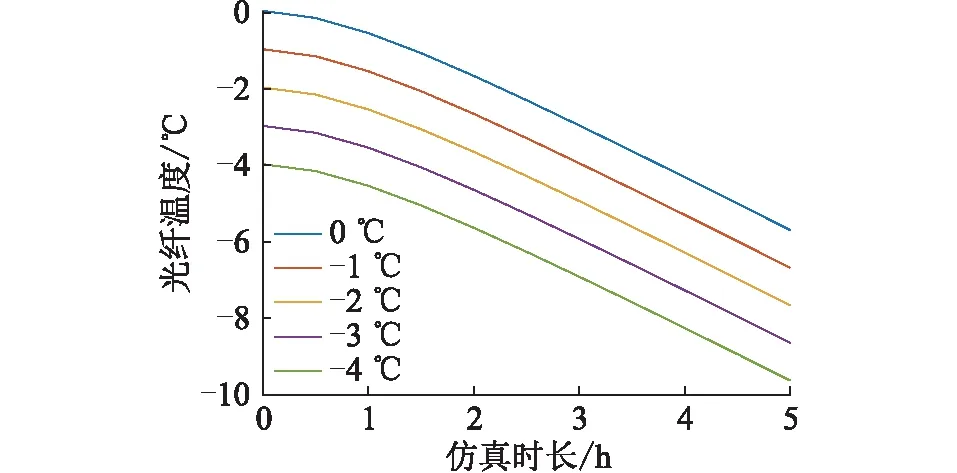
图14 不同初始环境温度时的未覆冰段光纤温度Fig.14 The temperature of the fiber in the OPPC with-out ice cover at different initial ambient temperatures

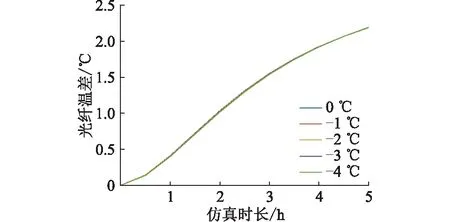
图15 不同初始环境温度时的光纤温差Fig.15 The temperature difference of the fiber in OPPCwith different initial values of ambient temperature

由图13和图14可知，在不同环境温度初始值情况下，覆冰段的光纤温度变化曲线与未覆冰段的光纤温度变化曲线的趋势相同，由图15则可知不同环境温度初始值时的温差变化曲线是基本重合的，可以得出光纤温度变化速度与环境温度初始值的大小无关，光纤温差的变化也与环境温度初始值的大小无关。

4.2 光纤温度与环境温度变化率的关系

设环境温度初始值为0 ℃，风速为0 m/s，覆冰的厚度为10 mm，覆冰的长度为1 m，环境温度分别以0 ℃/h，1 ℃/h，2 ℃/h，3 ℃/h，4 ℃/h下降，仿真5 h后得到不同环境温度变化率情况下的覆冰段线路光纤温度随时间变化曲线、未覆冰段线路光纤温度随时间变化曲线和线路光纤温差随时间变化曲线，如图16—图18所示。

图16 不同温度变化率时覆冰段光纤温度Fig.16 The temperature of the fiber in the ice-coatedOPPC with different temperature change rates

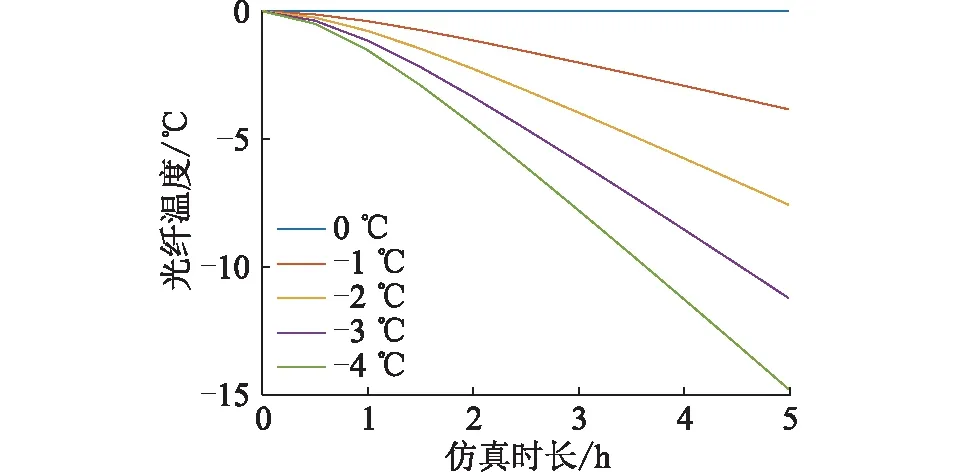
图17 不同温度变化率时未覆冰段光纤温度Fig.17 The temperature of the fiber in the OPPC withoutice cover with different temperature change rates

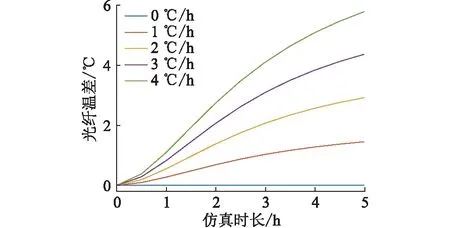
图18 不同温度变化率时光纤温差Fig.18 The temperature difference of the fiber in theOPPC with different temperature change rates

由图16和图17可知，当环境温度变化率为0 ℃/h时，即环境温度不变，光纤的温度不发生变化，此时线路已经达到热平衡状态，因此温度不再发生变化。为了更好地观察环境温度变化率对光纤温度变化的影响，整理图16和图17，得到不同环境温度变化速率情况下的光纤温差，如图18所示。由图18可知在相同时间点，两两相邻的温差变化曲线的差值相同，以5 h仿真时长为例，相邻光纤温差的差值为1.4 ℃。

5 光纤温度与覆冰厚度的关系

光纤温度分布与架空导线覆冰的厚度有关。为研究光纤温度与覆冰厚度的关系，设初始环境温度为0 ℃，环境温度以1.5 ℃/h下降，风速大小为0 m/s，覆冰长度为1 m，覆冰厚度分别取10 mm，15 mm，20 mm，25 mm，30 mm，35 mm。仿真时长5 h，得到不同厚度情况下的覆冰段和未覆冰段的光纤温度随时间的变化曲线，如图19和图20所示。

图19 不同覆冰厚度时未覆冰段光纤温度Fig.19 The temperature of the fiber in the OPPC without ice cover with different icing thicknesses

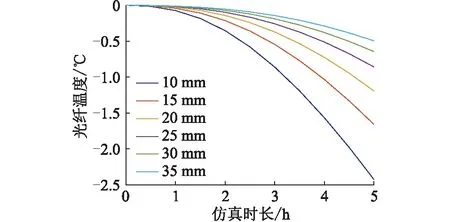
图20 不同覆冰厚度时覆冰段光纤温度Fig.20 The temperature of the fiber in the ice-coated OPPC with different icing thicknesses

在环境温度下降时，覆冰段温度的变化量小于未覆冰段。由图19得知，未覆冰段光纤温度变化仍与覆冰厚度有关，覆冰厚度越大，温度下降越慢，这是由于覆冰段与未覆冰段之间有热量传递，但覆冰厚度对未覆冰段温度的影响甚微。由图20可知覆冰厚度对覆冰段光纤温度的影响，覆冰越厚则温度下降时所释放的热量越多，导致单位时间内温度下降越缓，5 h后覆冰10 mm与35 mm的两光纤温度相差1.95 ℃。

根据图19和图20得出不同覆冰厚度情况下光纤温差，如图21所示。

图21 不同覆冰厚度时光纤温差Fig.21 The temperature difference of the fiber inthe OPPC with different icing thicknesses

由图21可知，覆冰越厚则温差的增长速率越接近环境温度变化率，但并不与环境温度变化率完全一致。冰厚35 mm时的光纤温差的增长速度为1 ℃/h，覆冰厚度会影响架空导线达到热平衡的速度，覆冰越厚则达到热平衡的速度越慢，这主要受冰的比热容影响，冰层越厚，释放热量的能力越强，环境温度下降时，覆冰段温度下降的速度越慢。

6 临界风速与环境温度和覆冰厚度的关系

由第3章的研究可知，光纤温差对风速很敏感，风速越高，对流散热越快，导致线路温差降低，易引起监测失效。光纤温差的产生是多种因素组合叠加的结果，根据前文的研究可知环境温度和覆冰厚度对光纤温差影响较大。此外，研究常见范围的环境温度和覆冰厚度下的不同风速对覆冰监测的影响是有必要的，因此第6章着重研究临界风速与环境温度和覆冰厚度之间的关系。

首先定义覆冰的临界风速。覆冰的临界风速是在不同环境温度变化率和不同覆冰厚度条件下，考虑满足BOTDA温度测量准确性的基础上，可有效识别架空导线覆冰状态的最大允许风速值。

6.1 临界风速与环境温度的关系

在4.1节中得出光纤温差变化与环境温度初始值无关，考虑到仪器的准确性，在6.1节中研究以温差0.5 ℃作为覆冰判据时的临界风速。6.1节的仿真参数为：覆冰长度为1 m，厚度10 mm，环境温度初始值为0 ℃，环境温度分别以0.8 ℃/h，1 ℃/h，1.5 ℃/h，2 ℃/h，2.5 ℃/h，3 ℃/h，3.5 ℃/h，4 ℃/h下降，仿真时长5 h，得到不同环境温度变化率下的临界风速，如图22所示。在环境温度变化速率小于0.8 ℃/h大于0 ℃/h时，临界风速为0 m/s。

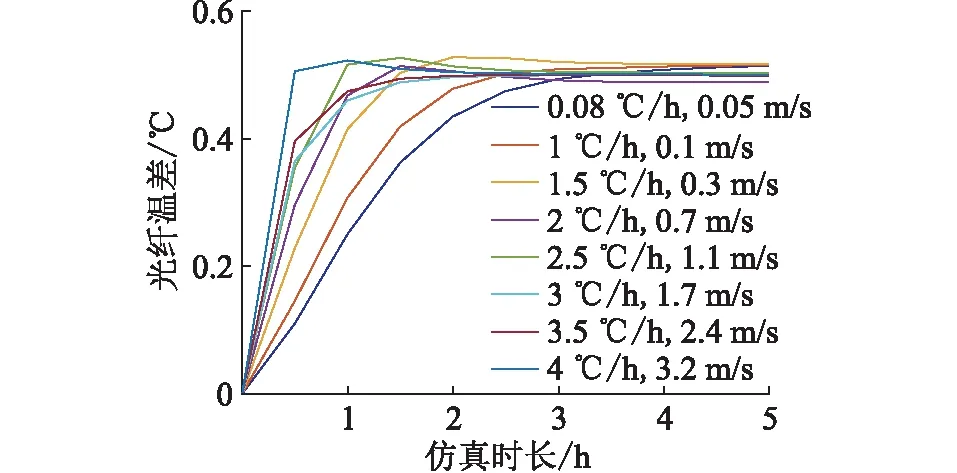
图22 不同环境温度变化率下的风速对光纤温差的影响Fig.22 The influence of wind speed on the temperaturedifference of optical fiber in OPPC under different environmental temperature change rates

根据仿真结果，可以拟合得到临界风速与环境温度变化率的关系式，如式(12)所示，拟合的效果如图23所示，其拟合误差平方和E1为2.55×10-3，确定系数R为9.998×10-1，其均方根误差E2为1.909×10-2。

(12)

式中：Vc为临界风速；ΔTamb为温度变化率。

图23 临界风速与温度变化率的关系Fig.23 The relationship between critical wind speed and temperature change rate

将式(12)所求得结果减去仿真所得数据，即为式(12)的温度公式误差，其分布如图24所示。其绝对误差的最大值为3.4×10-2m/s，误差最小值为2×10-4m/s，误差均值为1.1×10-3m/s，误差标准差为1.78×10-2m/s。

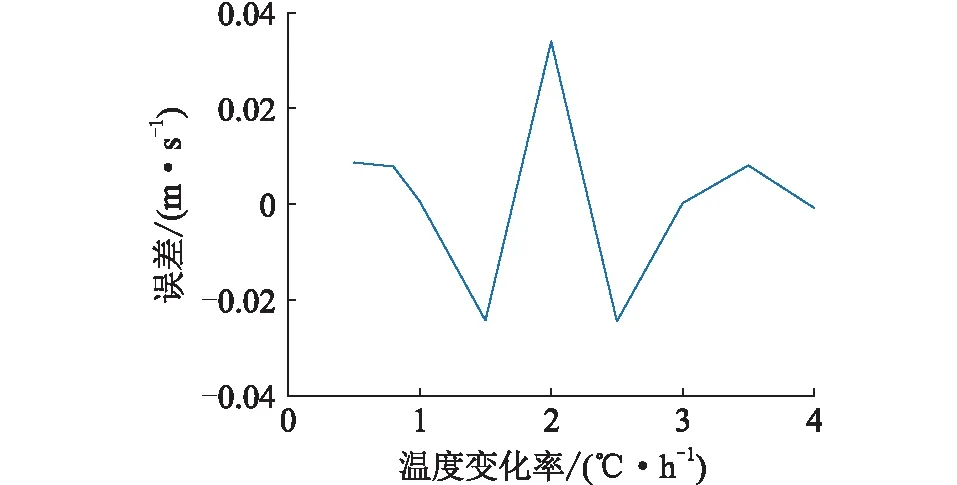
图24 不同温度变化率下临界风速公式的误差Fig.24 Error of critical wind speed formula under different temperature change rates

6.2 临界风速与覆冰厚度的关系

6.2节的仿真环境参数为：覆冰长度为1 m，环境温度以1.5 ℃/h下降，环境温度初始值为0 ℃，覆冰厚度分别以10 mm，15 mm，20 mm，25 mm，30 mm，35 mm进行仿真，仿真时长5 h，得到不同覆冰厚度下的临界风速，如图25所示。

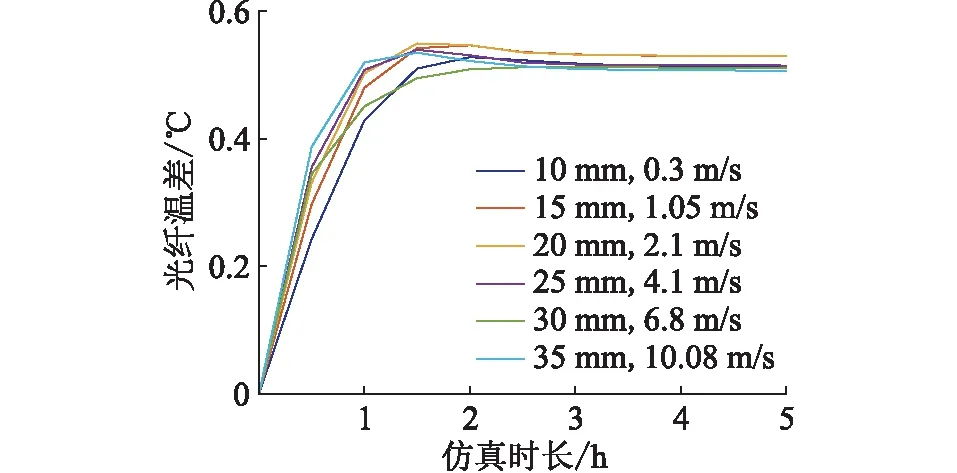
图25 不同覆冰厚度下的风速对光纤温差的影响Fig.25 The influence of wind speed on the temperature difference of optical fiber in OPPC under different icing thicknesses

根据仿真结果，可拟合得到临界风速与覆冰厚度的关系如式(13)所示，拟合效果见图26，其拟合误差平方和E1为1.746×10-2，其确定系数R为9.998×10-1，均方根误差E2为7.629×10-2。

Vc=0.000 274 3b3-0.000 221 4b2+0.012 78b

(13)

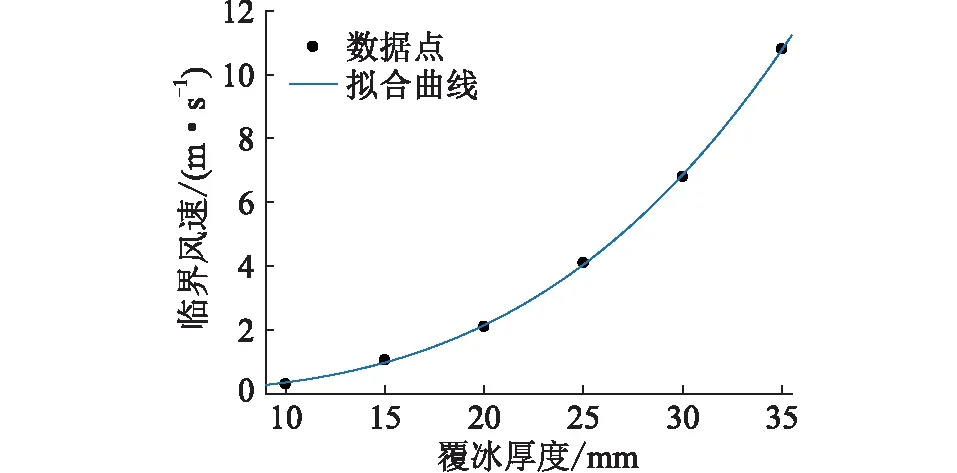
图26 临界风速与覆冰厚度的关系Fig.26 The relationship between critical wind speed and icing thickness

将式(13)所求得结果减去仿真所得数据，即为式(13)的温度公式误差，其分布如图27所示。其绝对误差的最大值为7.35×10-2m/s，误差最小值为2.09×10-2m/s，误差均值为-1.7×10-3m/s，误差标准差为5.91×10-2m/s。

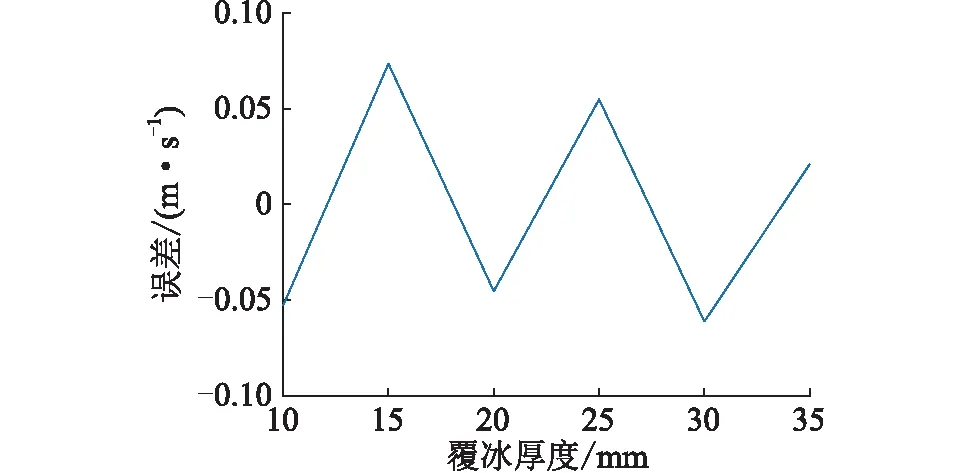
图27 不同覆冰厚度下的临界风速公式的误差Fig.27 Error of critical wind speed formula under different icing thicknesses

6.3 临界风速与环境温度和覆冰厚度关系

在6.1节和6.2节的基础上，研究不同环境温度变化率和覆冰厚度情况下的临界风速值。覆冰厚度分别取10 mm，15 mm，20 mm，25 mm，30 mm，35 mm，环境温度的变化率ΔT分别以0.8 ℃/h，1 ℃/h，1.5 ℃/h，2 ℃/h，2.5 ℃/h，3 ℃/h，3.5 ℃/h，4 ℃/h下降，设环境温度初始值为0 ℃，覆冰长度为1 m，仿真耗时15 d后得到临界风速与环境温度变化和覆冰厚度的关系如表2所示。

表2 临界风速值Table 2 Critical wind speed value m·s-1

根据表2风速值可知，环境温度变化率和覆冰厚度相对较小时，风速对架空导线达到热平衡的速度影响较大。风速大于24.5 m/s时，在实际运行中的意义有限，原因主要是风速为24.5 m/s时达到10级风，具有较大的破坏力，现实中该情况不易出现。表2中出现较大风速值的主要原因是温度变化率和冰层厚度较大时，风速虽然会加快对流散热，加快达到热平衡的速度，但影响程度较低，在高风速下才能彰显效果。

根据所得的风速、覆冰厚度和温度变化率，利用表2及二元函数插值方法可求得临界风速值。根据求得的临界风速可判断基于分布式光纤温度传感的方法是否可用于架空导线覆冰监测。

7 结论

文中利用有限元仿真软件建立了OPPC架空导线覆冰模型，覆冰架空导线在不同环境温度、风速和覆冰厚度情况下进行温度场计算分析，得出了以下结论：

(1) 对比了模型在是否考虑焦耳热物理场情况下的光纤温度变化情况，指出了在研究光纤温差时焦耳热对研究结果的影响可以忽略；

(2) 总结了光纤温差与环境温度之间的关系和光纤温度与架空导线覆冰厚度之间的关系，指出光纤温差与初始环境温度无关；

(3) 文中定义了判断架空导线覆冰的临界风速，分别给出了临界风速与环境温度的关系式和临界风速与覆冰厚度的关系式，以及在不同环境温度变化率和覆冰厚度下的临界风速值，可用于判断现实情况中分布式光纤温度传感方法是否可用于架空导线覆冰监测。