一种分段处理优选数据窗的双端测距算法

张灏， 薛明军， 王学超， 杨黎明， 李玉平， 陈福锋

(1. 国电南京自动化股份有限公司，江苏 南京 211153;2. 南京国电南自电网自动化有限公司，江苏 南京 211153)

0 引言

输电线路承担电能传送的重任，是电力系统中发生故障最多的地方。输电线路跨度远、排故难度大，因此故障测距技术对于快速修复故障、保障可靠供电有着重要意义。

线路保护故障测距功能快速、简洁，能够在第一时间输出测距结果。故障测距方法按测距原理主要分为行波法和故障分析法，根据测距所需信息来源又可分为单端量法和双端量法[1—2]。

行波法不受过渡电阻、系统运行方式变化、线路分布电容及负荷电流等影响[3—7]，但对装置采样频率及精度要求较高，且实际输电线路参数受频率影响，波阻抗具有不确定性，会影响行波法的计算准确性[8—10]。故障分析法简单、经济、易于实现，在电力系统中得到了广泛应用[11]。单端量故障分析法便于实现，尤其适用于单端供电线路，但对于双端供电线路，该方法易受对侧系统运行方式变化以及故障点过渡电阻的影响[12—14]。双端量故障分析法(简称双端测距)则不受过渡电阻和对侧系统阻抗影响，但须借助通信技术获取对侧数据[15—16]。随着光纤通信技术的发展，双端测距技术日趋成熟，且应用于电力系统大多数输电线路保护中。

对于一些严重故障，线路保护动作速度很快，若断路器动作速度也很快，则故障会在极短时间内被切除，此时故障测距数据窗很容易选取到故障切除后的时间段，或是故障起始暂态量较大的时间段，严重影响测距准确性。

为不失一般性，文中选取一个输电线路典型模型进行双端测距误差影响因素研究，针对性地提出一种基于分段处理的自适应优选数据窗实用算法，提高输电线路保护双端测距的准确性以及普适性。

1 集中参数双端测距基本原理和影响因素

1.1 集中参数双端测距基本原理

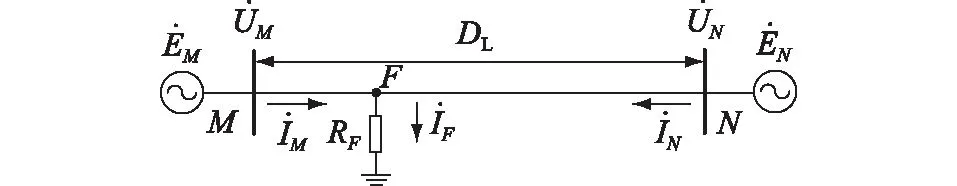
图1 线路故障示意Fig.1 Schematic diagram of line fault

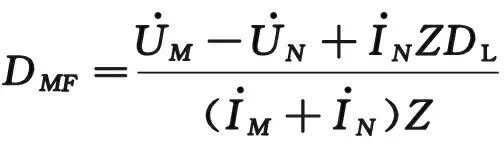
(1)

式中：DMF为双端测距结果；Z为线路阻抗。DMF理想计算结果为纯实数，由于是复数运算，且实际计算存在误差，因此取DMF的模值作为集中参数双端测距结果。在电力系统的不对称故障分析中广泛采用了对称分量法，将对称分量法用于故障测距，主流输电线路保护多选用正序分量进行双端测距计算，得到双端测距计算公式为：

(2)

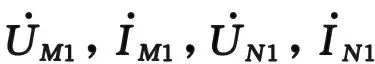
1.2 集中参数双端测距影响因素

集中参数双端测距主要适用于中、短距离输电线路，对于超高压、特高压长距离输电线路会存在较大误差，属于原理适用性范畴，文中不作讨论。

文中主要分析中高压中、短距离输电线路的集中参数双端测距影响因素，具体如下：

(1) 线路参数准确度。线路全长一般以实测值整定，误差较小。相比而言，受线路均匀性影响，单位长度正序阻抗存在一定误差，正常情况下误差按小于±5%计算。从分析的角度，将误差范围适当扩大，按±10%进行分析。

(2) 双端数据同步精度。输电线路保护通常采用乒乓同步算法，按电流基波同步角度误差小于±3°折算，同步时间误差小于167 μs。从分析的角度，将此范围适当扩大，按±200 μs进行分析。

(3) 数据窗选取位置。线路短路故障初期存在暂态过程，故障电流、电压随着时间发展趋于稳定，因此数据窗的选取倾向于尽可能靠后，但要避免选取故障切除后的数据窗。实际故障中断路器跳开故障的时间有快有慢，对于一些严重的金属性故障，动作时间快，故障电流、电压实际存在时间较短，故障测距数据窗的选取须兼顾暂态过程影响及故障切除后波形变化影响。为不失一般性，故障持续时间按60 ms进行试验分析，测距数据窗取[40 ms，70 ms]进行分析。

(4) 故障点与线路首端距离。在没有误差的情况下，测距结果就是故障点与线路首端距离，考虑到不同影响因素对不同位置故障点的测距影响程度不同，选取4个位置不同的故障点进行误差分析，故障点与线路首端距离分别为线路全长的0%，30%，50%，90%。

2 误差影响因素正交试验设计

2.1 正交试验设计

为定量分析上述因素对双端测距误差的影响，每个影响因素选取4个值进行仿真计算，分别记为水平1、水平2、水平3、水平4。但若要进行全面试验，则须进行44次仿真计算，工作量大。为提高试验效率，且达到同样的对比效果，利用正交试验设计方法进行试验。

正交试验设计是一种研究多因素、多水平的试验设计方法[17—19]，其根据正交性从全面试验中挑选出部分具有“均匀分散，齐整可比”特征的项目进行试验，可以大大减少试验数量，是一种效率高、计算速度快、便捷实用的试验设计方法。正交试验设计利用正交表来安排与分析多因素试验[20—26]。正交表用LN(mk)来表示，其中L代表正交表；N为试验次数，即正交表的行数；m为各因素的水平值，即正交表中的数字；k为因素个数，即正交表的列数。正交表须满足2个特点：一是均匀分散，即任一列中不同数字出现的次数相等；二是齐整可比，即任2列中，同一行所组成的数字对出现的次数相等。

2.2 集中参数双端测距影响因素分析及试验设计

选取4个影响因素，分别为线路参数误差(因素Ⅰ)、双端同步误差(因素Ⅱ)、数据窗选取位置(因素Ⅲ)、故障点与线路首端距离(因素Ⅳ)，每个影响因素选取4个水平值，选值如表1所示。

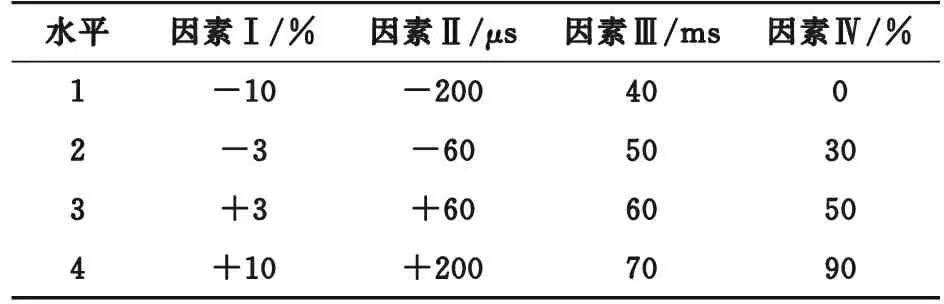
表1 试验设计影响因素及水平Table 1 Influencing factors and levels of experimental design

在EMTDC/PSCAD中搭建双侧电源线路模型，模型参数如表2所示。

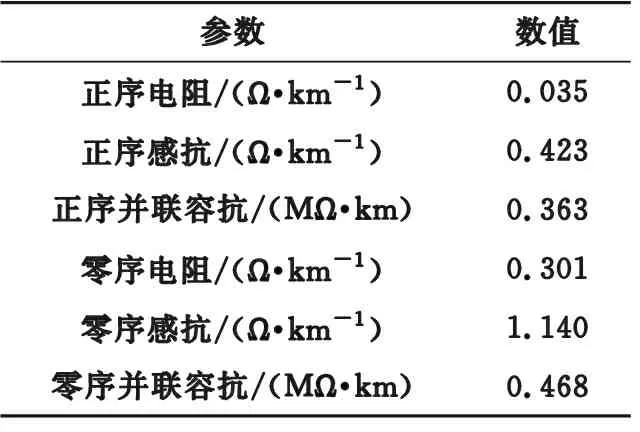
表2 仿真模型线路参数Table 2 Line parameters of simulation mode

模拟各故障点A相接地短路故障，故障切除时间取60 ms，合闸角取0°。以故障点与线路首端距离为线路全长的30%为例，图2、图3分别为本侧及对侧的仿真波形，包含两侧的三相电压、三相电流。在进行测距计算时，按照试验设计的不同因素及不同水平组合，人为增加不同误差进行计算，计算得到对应双端测距及误差结果。正交试验设计正交表L16(44)及试验结果如表3所示。

图2 仿真波形(本侧)Fig.2 Simulation waveforms (this side)

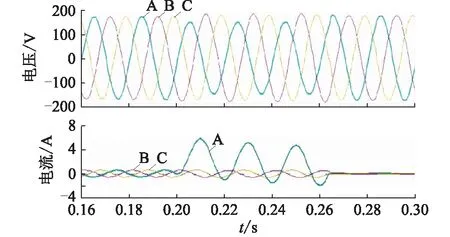
图3 仿真波形(对侧)Fig.3 Simulation waveforms (the contralateral)

表3 试验设计正交表及试验结果Table 3 Experiment design orthogonal table and experiment results

2.3 正交试验设计仿真结果及分析

为了对试验结果进行直观分析，计算各因素测距误差结果的均值与极差。均值为该因素在这一水平值下试验结果的平均值；极差为该因素不同水平值下均值的最大值与最小值之差。均值分析可以判断各因素不同水平对测距误差绝对值的影响，极差分析可以判断各因素对测距误差绝对值的影响。均值与极差计算结果如表4所示。

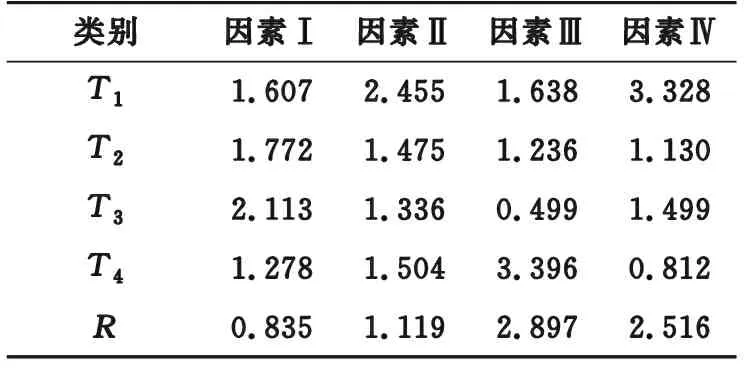
表4 均值与极差Table 4 Mean and range analysis km

表中T1，T2，T3，T4分别为4个水平的输出结果均值；R为极差，即T1，T2，T3，T4的最大值与最小值之差。由极差值可以看出，因素Ⅰ、因素Ⅱ对测距误差影响较小，因素Ⅲ、因素Ⅳ对测距误差影响较大。图 4为试验结果均值折线图。

图4 正交试验结果Fig.4 Orthogonal experiment results

由图4进一步分析，观察因素Ⅲ折线趋势可见，水平1～3误差在逐步减小，而水平4误差陡增，可知随着故障持续，故障电流、电压趋于稳定，暂态过程造成的误差随之减小，测距误差减小；当故障切除后，测距计算结果误差大幅增加。由因素Ⅳ折线可知，故障点与线路首端距离为线路全长的0%时误差最大，其他位置误差相对较小，这是由于影响因素对测距结果虚部产生的绝对误差在实部为0时对于复数模值的影响最大。

3 一种集中参数双端测距实用算法

3.1 测距数据窗常用选取方法

输电线路发生区内短路故障时，故障发生初始阶段，电流、电压均存在较大的暂态分量，影响工频量的准确提取；随着故障的发展，暂态分量衰减，故障波形趋于稳定，测距计算结果趋于准确；随后线路保护装置动作，跳开断路器，故障电流被切除，母线电压恢复，电流、电压不再反映故障特征，此时测距计算不再准确。因此，测距数据窗的选取原则一是尽可能选取波形趋于稳定的数据窗，二是避免选取故障切除后的数据。

实际应用中通常采用保护动作后固定一段延时为测距数据窗，这个延时小于断路器最快切除故障的时间，如30 ms，避免选取故障切除后的波形，一来保护动作说明故障特征已呈现，二来经过一段延时可保证电流、电压波形相对稳定。这种方法简单易实现，但断路器切除故障时间有快有慢，因此固定延时取值偏向保守，此时暂态分量还在衰减过程中，误差仍然偏大。且220 kV线路通常配置2套保护，虽然固定延时取值较短，但是2套保护动作时间可能有快有慢，另一套保护可能先动作跳开断路器，仍不能确保数据窗不包含故障切除后的数据。此外，故障点在线路首端时，双端测距结果受各因素产生的虚部误差影响较大，因此可通过改进方法避开这种情况。

3.2 分段处理的自适应优选数据窗实用算法

将平均法与测距变化门槛识别法以及故障点距离分段处理法相结合，提出一种集中参数双端测距实用改进算法。平均法是指在差动保护动作一定延时后陆续选取数据窗进行测距结算，当计算结果接近时，取其平均值；测距变化门槛识别法是指自适应选取一个门槛用于判别上述测距结果是否接近，门槛选取为差动保护动作后1周波与1.5周波测距结果的差值绝对值的2倍，差值代表了暂态过程造成的误差波动程度，2倍为可靠系数，此外本侧数据测距结果接近的同时对侧数据测距结果接近，以确保故障尚未切除；故障点距离分段处理法主要针对线路首端故障，本侧的首端则相当于对侧的末端，当用本侧数据计算结果小于40%线路全长时，则用线路全长减去对侧数据双端测距结果作为测距值。

本侧数据测距计算公式为式(2)，对侧数据测距计算公式如下：

(3)

式中：DNF为故障点距离N侧的距离。不难发现在取模值前须满足以下公式：

(4)

DMF20，DMF30分别为差动动作后20 ms，30 ms作为数据窗末端的本侧数据测距计算结果；DNF20，DNF30对分别为差动动作后20 ms，30 ms作为数据窗末端的对侧数据测距计算结果。选取门槛M如下：

M=2max(||DMF30|-|DMF20||,||DNF30|-|DNF20||)

(5)

DMF40，DMF50，DMF60，DMF70分别为差动动作后40 ms，50 ms，60 ms，70 ms作为数据窗末端的本侧数据测距计算结果；DNF40，DNF50，DNF60，DNF70分别为差动动作后40 ms，50 ms，60 ms，70 ms作为数据窗末端的对侧数据测距计算结果。

表 5为分段处理的自适应优选数据窗实用算法，按照序号依次进行相应条件判断，如果满足条件则输出测距结果，根据|DMF20|大小分段处理，输出相应测距结果DF。

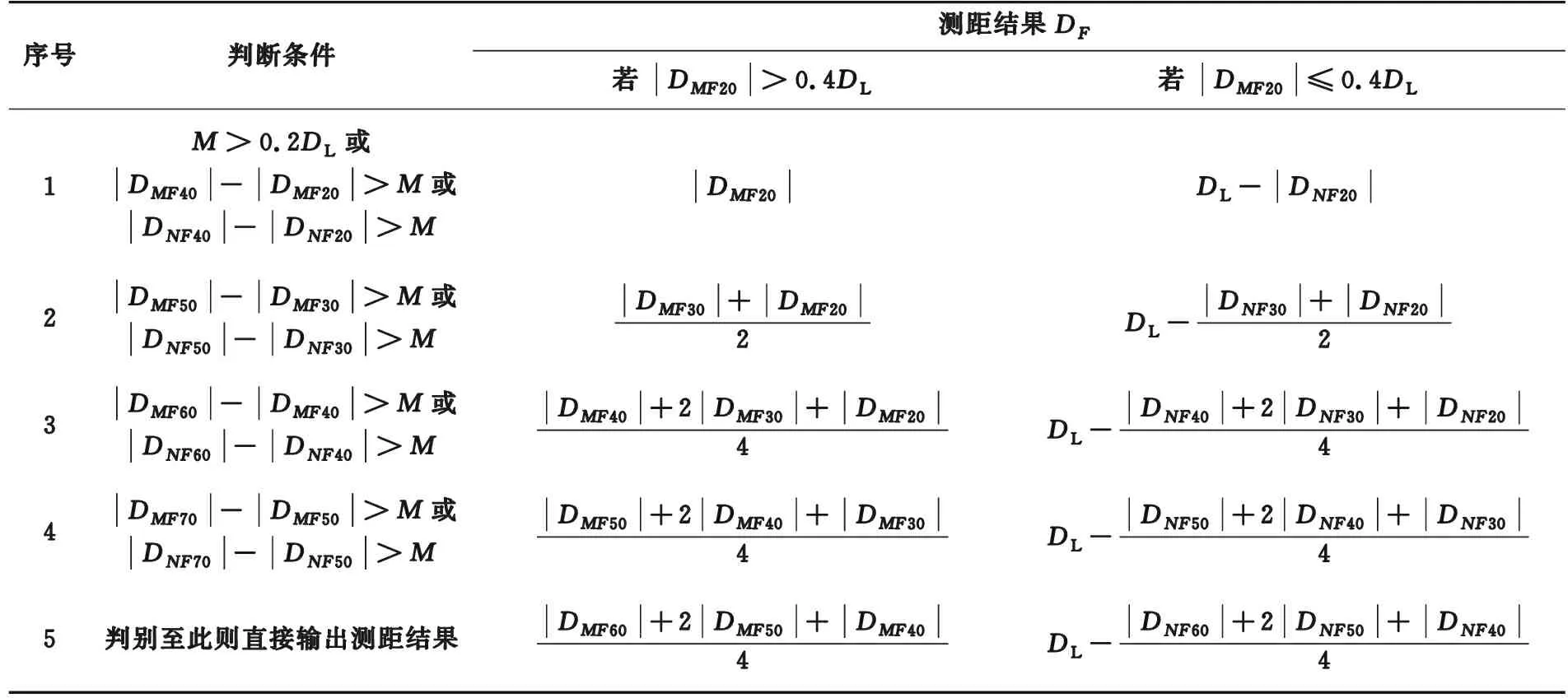
表5 分段处理的自适应优选数据窗实用算法Table 5 A practical algorithm of segmented adaptive optimization data window

通过此方法判别，一方面使得数据窗尽可能选取趋于稳定的波形；另一方面，通过本侧、对侧计算结果变化量判别，配合自适应门槛，更加可靠地选取故障切除前的数据窗。同时，通过故障区间分段处理，避开了直接计算结果接近0的区段，降低测距误差，提升了测距准确性。

3.3 改进算法验证

同样用上述正交试验进行验证，对因素Ⅲ选用2种数据窗选取方式进行对比，水平1和水平3选用分段处理的自适应优选数据窗实用算法(方式一)；水平2和水平4选用固定数据窗算法(方式二)，即保护动作后30 ms，假设保护动作时间为10 ms。通过仿真计算得到集中参数双端测距结果及绝对误差结果。正交试验设计正交表L16(44)及对比试验结果如表6所示。

表6 试验设计正交表及对比试验结果Table 6 Experiment design orthogonal table andcomparation of the experimental results

通过试验结果计算方式一与方式二测距误差绝对值的总均值与总极差，计算结果如表 7所示。

表7 对比试验均值计算结果Table 7 Mean calculation results of the contrast experiment km

通过验证可知，相比于传统的固定数据窗算法，改进算法的测距误差总均值大约缩小了一半，总极差也大约缩小了一半，说明改进算法受各因素影响程度大幅减小。

4 结语

文中针对220 kV的100 km双侧电源输电线路这一典型模型进行集中参数双端测距误差影响因素研究，针对实际工程中普遍出现的4个主要影响因素，通过正交试验设计方法以及仿真计算得到测距绝对误差，利用均值与极差分析方法，对比不同因素对测距绝对误差的影响程度，发现数据窗选取这一因素的总体影响程度最大，同时发现，相比于其他故障点位置，线路首端故障的测距误差受影响较大。

根据这2个特征，提出一种实用改进算法，一方面，将线路首端故障与其他故障位置进行区分，进行分段处理，另一方面，采用改进算法进行自适应数据窗选取，得出一种改进的双端测距综合计算方法。经验证，改进算法的测距绝对误差受影响因素影响程度总体上大幅降低，该方法可提升输电线路故障测距的准确性及普适性。