规模化超导储能磁体概念设计及系统经济性评估

陈孝元，张名顺，庞洲，雷一，李海波

(1. 四川师范大学工学院，成都 610101；2. 清华四川能源互联网研究院，成都 610023)

0 引言

为积极响应国家实现“2030年碳达峰、2060年碳中和”目标，电力行业要实现碳中和目标必须采用新能源代替传统能源进行发电。截至2020年底，我国风电、太阳能发电装机约530 GW，占总装机容量的24%。未来新能源仍将保持快速发展势头，预计2030年风电和太阳能发电装机达到1 200 GW以上[1]。在以新能源为主体的新型电力系统中，进一步考虑到清洁可再生能源的间歇性、波动性和随机性，电力系统将会面临着能量交互次数越来越多、容量越来越大的储能技术需求[2 - 5]。

2021年7月，国家发展改革委、国家能源局发布《关于加快推动新型储能发展的指导意见》，从国家层面首次提出装机规模目标：预计到2025年，新型储能装机规模达30 MW以上，接近当前新型储能装机规模的10倍[6]。新型电力储能将在推动能源领域碳达峰碳中和过程中发挥显著作用，预计到2030年将实现新型储能全面市场化发展，与电力系统各环节深度融合发展，装机规模基本满足新型电力系统相应需求。

与常规铜、铝导体相比，超导体具有零电阻损耗、高电流密度的技术优势。超导导线可代替铜导线绕制出高电感、大电流的磁体线圈，其储能磁体本体的运行损耗几乎为0。在这种新型的超导储能系统中，超导磁体以电磁能的形式存储电力，通过受控充放电电路及变流器系统与外部的新能源电力系统进行双向能量交互，以实现对电网电压和功率的平滑调控[7]。与目前主流的电化学储能电池相比，超导储能磁体本体具有更高的储能效率(约98%)、更快的响应速度(<1 ms)和几乎无限的充放电循环次数。其他新兴的储能技术如超级电容、飞轮储能等，大多也具备高效率、快速响应、使用寿命长等优势[8]，但目前仍存在一些实际工程应用问题。如：超级电容的单体模块电压、电流非常低，需要几百上千个模块串并联组成大容量储能装置，其内部模块之间的均流、分压、能量管理等软硬件控制系统复杂，故障率较高；飞轮储能存在超高速运动部件，其自身机械应力与转子高速运动将带来材料疲劳、机构断裂等安全隐患[9 - 10]。

与超级电容、飞轮储能相比，超导储能利用磁体电感储能，其单体模块的电流、功率和储能非常高，且不存在运动部件安全隐患。但是，由于超导材料制备成本昂贵，大容量超导储能的初期投资成本较高，目前市场化的程度较低。为了兼顾储能系统的性能指标及经济成本，小容量、高功率超导储能单元常被引入至常规电力储能装置，共同构成一种新型的混合储能系统。

文献[11]提出了一种用于风电场的超导-电池混合储能系统，其通过动态分配超导与电池储能的功率调节策略，充分利用波动性、间歇性的风能，降低整个可再生电网系统的运行成本；同时，还通过寻找超导储能投资成本和风电场运营成本之间的平衡，对超导储能参数进行了优化配置，有助于补偿风电系统的不稳定性。文献[12]提出了一种用于光伏微电网的超导-铅酸电池混合储能系统，其瞬态功率补偿性能要比单一的电池储能更佳，能够及时处理微电网的暂态故障问题；同时，混合储能系统保证了微电网在外部故障下的无缝模式切换，减少了公共连接点的故障电流。文献[13]提出了一种由超导储能、锂电池和燃料电池组成的混合储能系统，其采用燃料电池负载跟随控制，缓解了负载需求与可再生能源之间的动态功率平衡问题，并通过引入超导储能变流器的快速补偿和响应优势，减轻了燃料电池-锂电池复合系统的负载功率脉冲峰值需求。

为了降低混合储能系统中的超导储能单位储能容量成本，目前已有较多文献利用了自适应遗传算法、模拟退火算法等智能优化方案来对超导磁体结构进行优化设计和改进[14 - 16]。但是，以上优化算法过于复杂，还需要与具体磁体设计参数相结合形成约束条件，才能编程达到目标结果。若结合有限元软件进行磁体结构优化建模[17 - 19]，将会使得编程复杂，对超导领域的专业知识要求较高，不适合传统电气工程领域的工程技术人员掌握和使用。

本文对螺线管型超导磁体通过第一步单饼线圈数量和匝数优化、第二步单饼线圈间隙和增量优化，进行了双重结构优化设计，有效降低了单位储能容量的超导磁体投资成本，并进一步形成了规模化、可扩展的储能磁体阵列概念。针对传统的电化学电池储能充放电速度慢、生命周期循环次数少的技术缺陷，通过提高日均能量交互次数来降低超导储能的储能容量需求及初期投资成本，并通过减缓电池充放电循环操作以延长电池储能的使用寿命，为未来以新能源为主体的新型电力系统提供一种技术先进、经济可行的混合电力储能技术解决方案和实施路径。

1 超导储能基本原理

1.1 超导磁体的储能量

超导储能系统是以电磁能的形式存储能量，超导磁体储能量E的计算公式如式(1)所示[20]。

(1)

式中：L为超导磁体的电感量；I为超导磁体的运行电流。为了维持超导体的零电阻超导特性，超导磁体的实际运行电流必须小于其临界电流。

1.2 超导磁体的临界电流

典型的超导磁体由多个同轴的单饼线圈单元组装级联而成。每个单饼线圈单元则由多匝同心的超导带材线圈绕制而成。那么，超导螺线管磁体的整体临界电流取决于磁体内部每匝带材线圈临界电流的最小值。单根超导带材的临界电流Ic计算公式如式(2)所示[21]。

(2)

式中：Bpar、Bperp分别为超导带材周围的平行、垂直磁场分量；Ic0为超导带材的初始临界电流；α、γ、B1为超导带材的各向异性参数。

1.3 超导磁体的电感量

超导磁体的电感量取决于其内部单饼线圈的自感及所有单饼线圈之间的互感。每个单饼线圈单元的自感及相邻单元之间的互感计算公式如式(3)—(4)所示[22]。

(3)

(4)

式中：μ0为真空磁导率；N为线圈带材匝数；Da为线圈平均直径；ψ、φ为线圈绕制结构参数。

1.4 超导储能的功率补偿时间

当超导储能系统工作在稳恒功率交互状态时，可得到能量方程如式(5)所示。

(5)

求解式(5)，获得任意时刻t的超导磁体电流IL(t)计算公式如式(6)所示[23]。

(6)

式中：I0为磁体初始工作电流，其值必须低于磁体临界电流上限；Ron为超导储能变流器的等效损耗电阻；Pref为超导储能的稳恒放电负载功率。

定义从放电初始时刻开始到磁体电流值等于负载额定电流Iref时的时间长度为稳恒功率补偿时间Tmax，其计算公式可表示为：

(7)

由以上理论分析可知：超导储能的补偿功率峰值取决于其运行电流值，在磁体优化设计过程中需要尽可能提高磁体临界电流，以满足更高功率补偿需求的新能源电网能量交互场合。同时，超导储能的功率补偿时间长度则由储能容量及运行电流上限共同决定。在集成了小容量、高功率超导储能单元的混合储能系统中，需要根据能量交互需求与常规储能性能特点，择优匹配超导电感、临界电流与储能量三者之间的关系，尽可能兼顾优良的储能技术和适中的经济成本。

2 螺线管型磁体的结构优化设计平台

2.1 磁体结构优化设计基础

图1给出了不等轴向间隙的螺线管型超导储能磁体结构示意图。螺线管型超导磁体由Q个单饼线圈构成，其中单侧移动m个单饼线圈，使得单饼线圈轴向间隙不相等。具体来说，m个单饼线圈的间距由相邻气隙间距增量Δx和单饼的最小气隙间距g组成，位于磁体中间区域的(Q-2m)个单饼线圈的轴向间隙相等为d。

图1 不等轴向间隙的螺线管型超导储能磁体结构示意图Fig.1 Solenoid magnet with unequal axial gaps between pancakes of superconducting energy storage system

如图2所示，在螺线管型超导磁体中的Q个单饼线圈中，每个单饼线圈均由N匝超导带材绕制而成。螺线管型超导磁体的临界电流计算过程如下：首先将单匝导线划分为n段计算区域，计算每段的临界电流分量Ic(i,j,k)(i∈1～Q，j∈1～N，k∈1～n)；其次，将n段计算区域的临界电流分量求和，得到这一匝导线的总临界电流；然后，计算N匝线圈中每匝导线的总临界电流，通过比较获得该单饼N匝导线中的临界电流最小值；最后，计算Q个单饼中每个单饼的临界电流最小值，通过比较获得Q个单饼中的临界电流最小值，即为螺线管磁体的临界电流，计算公式如式(8)所示。

Ic=min{min{sum[Ic(i,j,k∈(1,n))],
j∈(1,N)},i∈(1,Q)}

(8)

图2 单饼线圈的内部带材分层计算结构示意图Fig.2 Schematic diagram of internal layered calculation structure of single-pancake coil

在计算螺线管超导磁体的电感量时，需要综合考虑单饼自感及饼间互感的影响。计算任何两个单饼之间的互感，可忽略其余单饼，并将这两个单饼线圈及内部间隙区域视为一个短螺线管来计算。以此类推，综合计算Q个单饼线圈自感及互感，螺线管型超导磁体的总电感计算公式总结如式(9)所示。

(9)

式中：L为每个单饼线圈的自感值；M1,i+1为第1个单饼线圈与第(i+1)个单饼线圈的互感值。

2.2 磁体结构优化设计软件开发

螺线管型超导磁体的总体设计和优化过程如图3—4所示。该过程分为两步[24]：1)单饼线圈尺寸优化设计；2)饼间气隙距离优化设计。

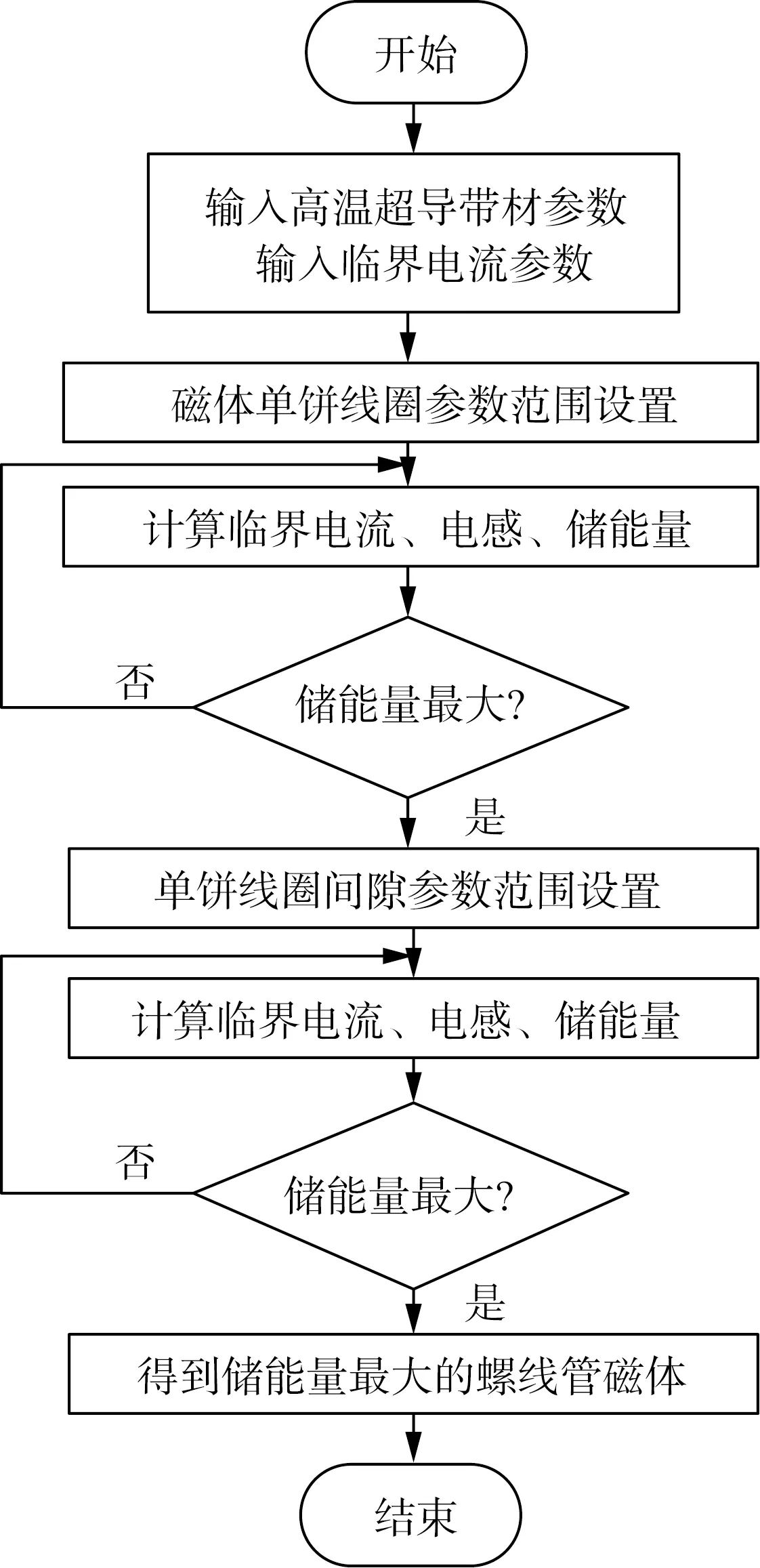
图3 螺线管型超导磁体结构优化流程图Fig.3 Flow chart of structural optimization of the solenoidal superconducting magnet

图4 螺线管型超导磁体结构优化过程和总体设计框图Fig.4 Overall design diagram for structural optimization of the solenoidal superconducting magnet

第1步，首先输入超导带材参数，如：超导内芯宽度Whts、封装带材宽度Wtape、封装带材厚度Ttape、带材绝缘厚度Tins、带材总长度S，临界电流参数α、γ、B1、Ic0；然后，输入单饼线圈参数，如：单饼数量Q、每个单饼的线圈匝数N、内半径Ri、外半径Ro、每匝线圈的分段数量n、相邻单饼之间的固定轴向间隙d；最后，在给定某些固定参数(如：带材参数)的基础上，进一步在其余可变参数(如：单饼参数)的上下限范围内按预设步长变化，依次计算磁体的临界电流、电感量和储能量，并通过冒泡排序法比较获得储能量最大时的磁体结构参数(相等轴向间隙)。

第2步，首先将第1步输出参数(如：Ri、Ro、N、Q)作为这一步的输入参数；然后，输入单饼的最小气隙间距g、相邻气隙间距增量Δx、单侧移动单饼个数m；最后，在以上3个可变参数的上下限范围内按预设步长变化，通过冒泡排序法比较获得储能量最大时的磁体结构参数(不等轴向间隙)。

与目前现有的智能优化算法(如：遗传算法、模拟退火算法)相比，本文所开发的结构优化设计软件通过以上两个优化设计步骤，可以简化超导储能磁体的结构优化设计工作量，提升软件整体运行速度。同时，该软件在优化设计过程中可以充分考虑实际超导储能磁体制造工艺精度及低温杜瓦尺寸限制等一系列几何结构参数，且无需掌握应用超导领域的专业技术知识及复杂优化算法模型。

为了进一步验证本文所提出的不等间隙螺线管型磁体结构优化设计方法及所开发的结构优化设计软件的实用性，以一个小型超导螺线管实验磁体为参照对象，进行了实验测试与计算结果对比分析。该实验磁体由6个双饼线圈同轴安装组成，每个双饼的内半径、外半径和高度分别为100 mm、109.6 mm和9.6 mm。从磁体一端到另一端的双饼线圈轴向间隙分别设置为20 mm、18 mm、16 mm、18 mm和20 mm，构成了不等间隙型超导磁体结构[21]。经过实验测试，该超导磁体的临界电流和电感量分别为123.8 A和10.1 mH。对比而言，本文所开发的结构优化软件的计算结果分别为103.2 A和9.61 mH，整体误差较小，满足超导储能磁体的工程设计精度要求。

3 MJ级超导磁体结构优化设计案例分析

3.1 相等间隙螺线管型磁体结构优化

为了实现规模化超导磁体概念设计及经济性评估，需要实际设计兆焦级螺线管型超导磁体单元进行实例分析。本文以10 km长度的超导带材为总导线使用量，用于设计MJ级超导储能系统中的核心超导磁体装备。

图5给出了第一步优化设计流程获得的储能量数据变化曲线。可以看出：当单饼线圈数量为140、150、160，单饼内部匝数在5～13之间变化时，可获得储能最大值为2.344 MJ。储能最大值所对应的磁体临界电流为912.212 A、电感量为5.634 H。此时，单饼个数为150，单饼匝数为11匝，内半径为0.962 m，外半径0.967 m。

图5 相等间隙的螺线管型超导磁体结构优化结果Fig.5 Optimization results of constant-gap solenoidal superconducting magnet

3.2 不等间隙螺线管型磁体结构优化

在上一步的优化结果基础上对影响磁体间隙改变的单饼最小气隙间距g、相邻气隙间距增量Δx、单侧移动单饼个数m进行第二步优化。详细的优化过程及中间环节参数结果如图6所示。

图6 不等间隙螺线管型超导磁体结构优化结果Fig.6 Optimization results of varying-gap solenoidal superconducting magnet

1)任意设置单侧移动单饼个数为2，单饼的最小气隙间距范围为2～6 mm，相邻气隙间距增量范围为1～7 mm，可获得图6(a)中的储能量数据；

2)设置单侧移动单饼个数范围为1～20，固定单饼的最小气隙间距为2 mm，相邻气隙间距增量为6 mm，可获得图6(b)中的储能量数据；

3)固定单侧移动单饼个数为5，设置单饼的最小气隙间距范围为2～6 mm，相邻气隙间距增量范围为1～3 mm，可获得图6(c)中的储能量数据；

4)设置单侧移动单饼个数范围为1～20，固定单饼的最小气隙间距为2 mm，相邻气隙间距增量为2 mm，可获得图6(d)中的储能量数据；

5)固定单侧移动单饼个数为8，设置单饼的最小气隙间距范围为2～6 mm，相邻气隙间距增量范围为1～3 mm，可获得图6(e)中的储能量数据；

6)设置单侧移动单饼个数范围为1～20，固定单饼的最小气隙间距为2 mm，相邻气隙间距增量为1 mm，可获得图6(f)中的储能量数据；

7)固定单侧移动单饼个数为12，设置单饼的最小气隙间距范围为2～6 mm，相邻气隙间距增量范围为1～3mm，可获得图6(g)中的储能量数据；

8)设置单侧移动单饼个数范围为1～20，固定单饼的最小气隙间距为2 mm，相邻气隙间距增量为1 mm，可获得图6(h)中的储能量数据。

在对单侧移动单饼个数、单饼的最小气隙间距、相邻气隙间距增量3个参数数值进行综合优化后，最终获得单饼个数为150、匝数为11时的最大储能量数据。综上所述，使用10 km超导带材绕制的螺线管型超导磁体时，单饼个数为150，单饼匝数为11，内半径为0.962 m，外半径为0.967 m，单侧移动单饼个数为12，单饼的最小气隙间距为2 mm，相邻气隙间距增量为1 mm。此时，最大储能量为3.079 MJ，临界电流为1 054.204 A，电感量为5.542 H。与第一步的优化结果相比，储能量提高了31.36%，临界电流提高了15.57%。那么，采用本文开发的不等间隙螺线管型超导磁体结构优化方案，既有效降低了超导储能系统的单位储能量造价成本，还可以提高线路能量补偿的瞬时功率峰值。

4 轴间平行的螺线管型超导储能磁体阵列

在优化设计完成的3 MJ螺线管型超导磁体基础上，可进一步构建轴间平行的超导储能阵列系统，以实现规模化的超导储能系统概念设计。如图7所示，以两个轴间平行的超导磁体为例，当轴间间距在2～4 m之间变化时，互感值逐渐减小。当轴间距离为2.8 m、3.6 m时，互感值仅为螺线管自感值的5%、2%。

图7 两个轴间平行的超导磁体互感变化结果Fig.7 Mutual inductance of two axial-parallel superconducting magnets

以3 MJ螺线管型超导磁体为基础储能单元，进一步构建q×q阶的轴间平行超导储能磁体阵列。图8给出了螺线管阵列内部的总互感与总自感之间的比例参数数值变化结果。

图8 互感/自感比例与螺线管阵列阶数之间的关系Fig.8 Relation between the order number of magnet array and the ratio of mutual inductance to self inductance

从图8可以看出：当螺线管阵列的阶数线性增加时，互感/自感比例也随之增大，并逐渐趋于饱和。在相邻螺线管轴间间距为2.8 m、3.6 m的情况下，互感/自感比例的饱和值近似为5.7%、2.5%。由于互感/自感比例的数值大小实际表征了磁体阵列内部多个超导磁体之间的磁链交互程度，较小的比例值即代表相互之间磁场几乎不受影响。那么，每个超导磁体单元的临界电流、电感量和储能量可近似认为维持不变。

5 超导储能成本计算与系统经济性评估

5.1 储能成本计算原理

第4节对螺线管型超导磁体进行了优化设计，获得一个由10 km超导带材绕制的3 MJ超导磁体。单个超导磁体的投资成本主要为超导材料购置成本，其计算公式如式(10)所示。

Csmes=CTape×l

(10)

式中：CTape为超导带材单价，200元/m；l为绕制磁体所需的带材长度，m。

储能系统的总成本CTotal主要由投资成本与运行成本组成，如式(11)所示。

CTotal=CInvest+Y×CO&M

(11)

式中：投资成本CInvest由储能容量E及单位储能成本CUint决定；运行成本CO&M由年均电能损耗带来的电费及运行时间长度Y决定。具体计算公式如式(12)所示。

CInvest=E×CUnit=M×Esmes×CUnit

(12)

CO&M=365×(1-η)×ETotal×Cel

(13)

式中：Cel为单位电能电费；Esmes为单个超导磁体储能量；M为超导储能磁体的数量；η为储能效率；ETotal为储能系统每天与新能源电力系统实时交互的总电能容量。

定义储能系统完成额定储能容量的充放电操作为一次循环次数，那么，储能系统每天的充放电循环次数K的计算公式如式(14)所示。

(14)

5.2 系统经济性评估

超导储能作为功率型储能装置，拥有非常高的功率密度和非常快的响应速度。在清洁可再生能源富集的微型电网中，超导储能可用于快速调节系统瞬时功率和稳定线路暂态电压。根据文献调研，在目前的实际电网应用场合中，MJ级容量的超导储能装备主要用于秒级的瞬态功率补偿[25 - 32]，GJ级容量的超导储能装备则主要用于分钟级的短时功率补偿[33 - 36]。

文献[25]将3.8 MJ超导储能磁体应用于1.2 MW可再生能源发电系统(风光联合发电系统)，其利用超导储能的高功率、快速响应特性对可再生能源的持续、高频功率波动进行有效缓冲抑制，通过平滑其瞬态输出功率以提升电网联络点的稳定性，防止电源侧波动向新型电力系统的用户侧渗透传播。在性能测评过程中，超导储能磁体在3 s时间内完成一次能量交互操作(储能容量变化约10%)，将可再生能源的最大输出功率波动从约60%降低到15%。文献[33]提出了一种集成48 GJ超导储能和125 GWh液氢储能的混合储能系统设计，将其应用于GW级容量的大型可再生能源电站，通过在线均衡发电侧与负荷侧的瞬态功率需求，有效减轻负载突变导致的电网功率波动和频率震荡。在性能测评过程中，超导储能磁体可以在几秒至几分钟时间内，瞬态吸收约150 MW的过剩功率，或对外补偿约300 MW的功率凹陷。在源-荷供需不平衡的动态功率补偿过程中，通常在2～4 min之内即可完成一次与外部线路之间的48 GJ储能全容量交互操作，避免以氢气为燃料的燃气轮机的频繁启停及输出功率快速调整操作，有效提升整个系统的供电品质，并可望延长燃气轮机的使用寿命。

但是，由于目前的超导材料及其绕制的超导磁体成本较高，大容量超导储能的经济性较差。相比而言，电池储能则具备更高的能量密度和更低的投资成本，能够为微型电网提供较长时间的能量补偿和稳定供电[37]。但是，电池储能的储能效率相对较低，典型的大规模电池储能本体效率约为85%，储能变流器充放电效率约为95%[38 - 39]。而且，电池充放电循环次数有限，使用寿命通常小于5 a。超导储能与电池储能的性能参数对比如表1所示[40 - 44]。

表1 超导储能与电池储能的性能参数对比Tab.1 Specifications comparison of superconducting and battery energy storage

本文将对接入超导储能和电池储能的微型电网进行系统投资和运行成本分析，以评估超导储能的经济性和实用性。以10 km超导带材绕制的3 MJ超导磁体为基础储能单元，形成60×60超导储能磁体阵列，实现10.8 GJ/3 MWh的规模化超导储能容量。在案例分析中，设置每天的超导充放电循环次数为200次，其对应的日均能量交互容量达到600 MWh。为了实现相同容量情况下的对比分析，选用300 MWh储能容量的电池系统，并设置每天的电池充放电循环次数为2次。电池全生命周期运行5 a将达到3 650次充放电操作，需要重新更换全新的电池储能系统。案例分析中的储能系统容量与充放电循环次数如表2所示。

表2 储能系统容量与充放电循环次数Tab.2 Energy storage capacities and charge-discharge cycles

利用式(10)—(14)对超导储能和电池储能进行成本计算。在日均能量交互容量达到600 MWh的情况下，超导储能容量仅为3 MWh/10.8 GJ，其初期投资成本为72亿元；电池储能容量达到300 MWh，初期投资成本为21亿元。此外，若考虑超导储能的制冷系统投资成本，需要计算其系统漏热及制冷功率。典型的低温漏热值为50 W/kA，则3 MWh/10.8 GJ超导储能的总漏热估算为180 kW。目前低温制冷机的单位投资成本为72.22万元/kW[45]，折算人民币总投资成本约为1.3亿元。因此，与超导储能磁体的导体材料成本相比，制冷系统投资占据比例非常小。

在与外部微型电网进行能量交互操作的过程中，储能系统会产生一定的电能损耗。根据表1中给出的储能性能对比参数，超导储能和电池储能的整体充放电效率分别达到93.1%和80.7%。按照0.5元/kWh电费进行折算，超导储能每年的电力损耗费用为755.6万元，电池储能每年的电力损耗费用为2 107.9万元。若考虑目前市场上大容量电池新产品的储能效率可达到90%，则每年电池储能的电力损耗费用降低为1 587.8万元。但是，与300 MWh电池储能的购置成本相比，其日常运行的电力损耗费用比例非常低，储能系统的总投资成本主要取决于电池购置和更换。

在运行一定时间后，对两种储能系统的投资成本、运行成本进行分析，如图9—10所示。

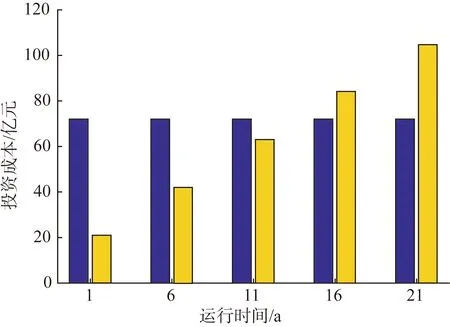
图9 不同运行时间下的储能投资成本对比Fig.9 Investment cost comparison of two energy storage schemes under different operating hours

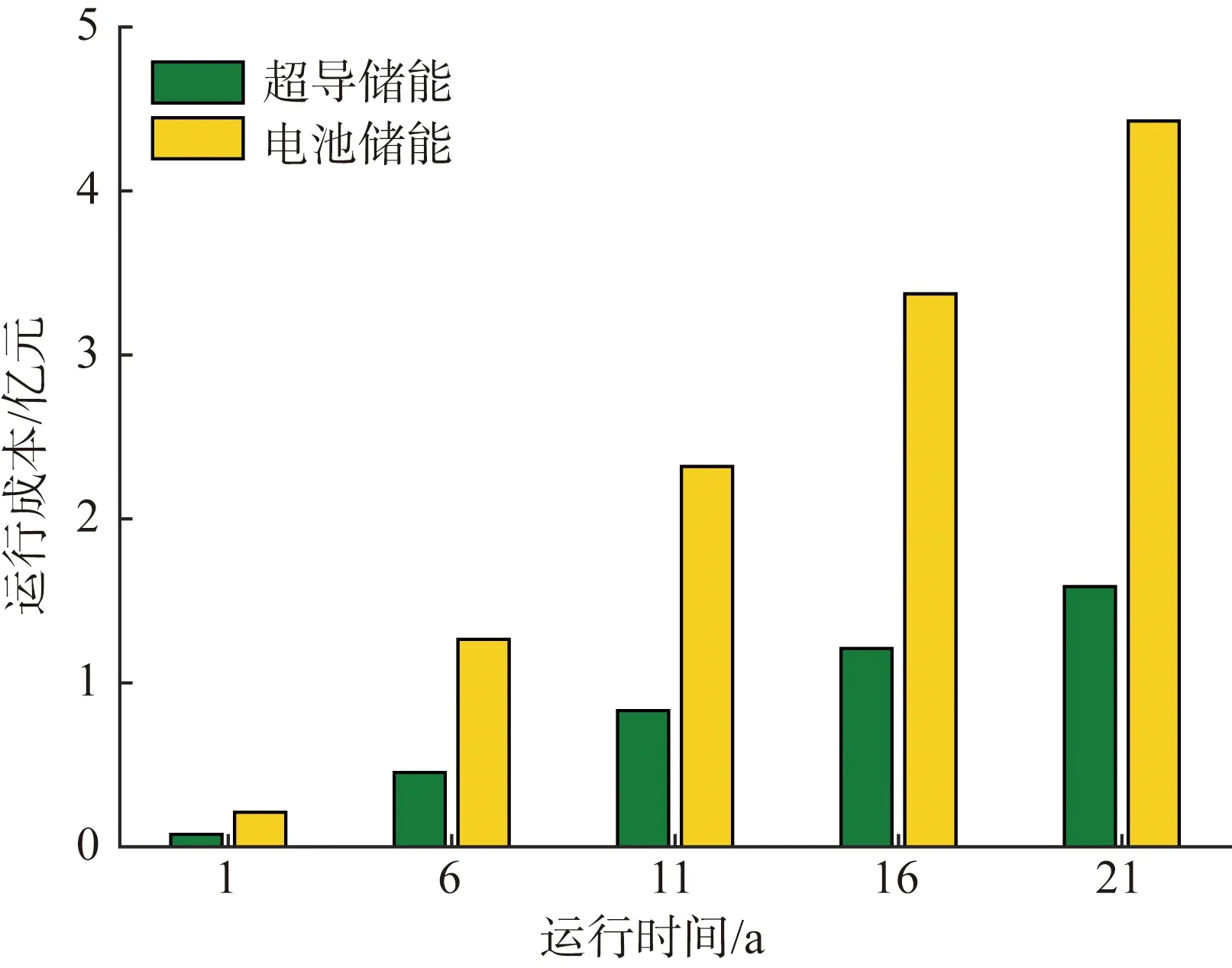
图10 不同运行时间下的储能运行成本对比Fig.10 Operating cost comparison of two energy storage schemes under different operating hours

可以看出：在运行初期，因超导储能自身投资成本因素，其投资成本远高于电池储能。但由于电池生命周期短，持续5 a运行后电池循环次数达到上限，必须更换电池才能继续工作，进一步增加了投资成本。而超导储能具有几乎无限的生命周期，典型的运行年限可达到30 a或以上。在日常的能量交互操作过程中，电池储能损耗带来的运行成本已达到超导储能的6倍，其配套的冷却降温设备及过热安全保护设施也将带来额外的经济成本。此外，电池储能系统更换后将形成300 MWh的退役电池组，其后续的梯次利用及废弃物处理也将带来较高的经济成本。

在经过16 a的储能运行后，电池储能总成本达到87.37亿元，超出超导储能总成本约14.16亿元。而且，随着运行时间的持续增加，电池储能和超导储能总成本差额将会越来越大。因此，从长期储能运行的角度，超导储能更具备经济优势。而且，随着超导材料制备技术的发展，特别是商业化的高温超导带材价格预计将以每年10%速度下降[46]，由带材绕制而成超导储能磁体成本也将进一步降低，超导储能技术在我国大规模推进新型储能发展历程中将具备越来越好的技术和经济潜力。

同时，在以新能源为主体的新型电力系统中，风力、光伏等清洁可再生能源的间歇性和波动性将会给储能系统带来能量交互次数越来越多、能量交互容量越来越大的技术需求[47]。考虑单一电池储能全生命周期为5 a、日均充放电循环次数为2次的实际情况，其额定储能容量将会变得非常大。在10.8 GJ/3 MWh超导储能系统的日均充放电次数达到330次的情况下，其等效的电池储能额定容量已达到495 MWh。

图11给出了10.8 GJ/3 MWh超导储能每天实现不同充放电循环操作次数下的总成本变化规律。给定相同的10 a运行时间，随着每日能量交互次数的持续增加，超导储能总成本将会逐步低于电池储能。以500次/d的能量交互次数为例，超导储能实际容量需求将会降低至电池储能容量的1/250。此时，电池储能的总成本已达到110.3亿元；而超导储能总成本仅为73.9亿元，相比电池储能下降了约33%。因此，在能量交互需求日益频繁的新能源电力系统中，超导储能系统有望实现更低的储能容量需求，进而大幅度降低其初期投资成本，获得更高的技术与经济效益。

图11 不同循环充放电次数下的储能总成本对比Fig.11 Comparison of the cost of energy storage schemes under different energy charge-discharge cycles

需要说明的是，上述超导储能与电池储能的经济评估工作主要是基于电池全生命周期充放电次数有限的性能研究角度。如果要进行较为全面、系统的储能经济效益评估，后续需要对超导储能系统中的超导带材、磁体制造、制冷系统、变流电路、日常运维等一系列成本进行综合建模与分析。由于超导储能自身属于一种新兴的、尚未成熟商业化运营的电力储能装备，系统研制成本及运维成本很难进行准确的量化计算和经济评估。本文所提出的经济效益初步评估方法及规律，将为含超导储能的混合电力储能装备经济评价提供一些基础数据参考。

6 结论

本文对螺线管型超导磁体通过第一步单饼线圈数量和匝数优化、第二步单饼线圈间隙和增量优化，进行了双重结构优化设计。在给定相同的10 km超导线长度的情况下，改进后的超导储能磁体临界电流和储能量分别提高了约16%和30%，有效降低了单位储能容量的超导磁体投资成本，并提高了超导储能的运行电流及充放电功率峰值。进一步形成了规模化、可扩展的储能磁体阵列，概念设计了10.8 GJ/3 MWh超导储能系统。针对电池储能充放电速度慢、生命周期循环次数少的技术缺陷，通过提高日均能量交互次数来有效降低了超导储能的初期投资成本。当超导储能的满负荷充放电操作达到500次/d，其实际容量需求将会降低至电池储能容量的0.4%，且持续运行10 a后的超导储能总成本仅为电池储能的67%。因此，在以新能源为主体的新型电力系统中，能量交互次数越来越多、容量越来越大的迫切需求将会给超导储能系统的大规模应用带来较好的市场化、产业化发展机遇。特别是在新能源电网中的直流侧应用场合，超导储能非常适合高频次、高峰值能量交互，进而有效抑制新能源暂态波动及响应二次调频需求。同时，若进一步融合目前主流的电化学储能技术，超导储能与电池储能有望形成高功率与高容量兼备、高效率与低成本兼容的混合储能技术新思路，有效提高电力储能的技术与经济效益。