直流配电网中多退役电池储能组并联的协调控制
张华,苏学能,万承宽
(1. 国网四川省电力公司电力科学研究院,成都610000;2. 成都星河科技责任有限公司,成都610041)
0 引言
随着化石能源的逐渐枯竭和世界各国电池技术的进步,电动汽车开始得到广泛的普及和应用[1 - 2]。然而,充放电次数的增加会使电池性能不断下降。当动力电池的荷电状态(state of charge,SoC)降至80%时,它们将无法满足电动汽车的严格要求[3 - 4]。随着电动汽车数量的增加,越来越多的锂离子电池出现了不同程度的电池老化、容量衰减和一致性降低的问题,导致无法充分发挥最大的经济效益[5 - 7]。因此,鉴于配电网电化学储能系统对电池性能要求较低的特点,将退役电池二次利用作为配电网储能系统是一种很好的方法[8 - 9],可以充分挖掘其剩余价值,获得更大的经济和社会价值。
近年来,退役动力电池作为储能系统在直流配电网中的二次利用得到了迅速的应用和发展。由于电池电压差大、异质性多样化的特点,传统的集中式拓扑难以实现不同类型和梯度的退役电池重组。因此,通常需要提前对退役电池进行筛选和分组以形成储能系统,并将其应用于直流配电网[10]。文献[11]提出了一种基于机器学习算法的模块级快速排序和重组方法。通过研究充电曲线与电池剩余有效容量之间的相关性,采用基于支持向量机的快速排序模型对电池容量进行评估,并采用改进的k-均值算法对退役电池进行重组。文献[12]建立了从单个电池到电池模块的相关函数,根据电池模块的参数描述退役动力电池的外部特性,利用最小二乘法对剩余寿命周期健康状态(state of health, SoH)曲线进行拟合和排序。
因此,带变流器的多支路拓扑在退役电池二次利用中显示出更明显的体系结构优势[13 - 14]。在直流配电网中,多分支储能系统通过在直流母线上并联多个DC/DC转换器来实现。这种拓扑结构不仅具有良好的兼容性,而且具有很强的可扩展性,特别适用于光伏等可再生能源发电的接入,但它主要考虑不同的退役电池储能系统之间的协调应用,没有涉及各储能系统中每个退役电池的最佳运行[15 - 16]。
退役电池储能系统运行期间健康状态的一致性是不同退役电池二次利用的关键因素之一[17 - 20]。由于退役动力电池退役前的不同应用场景和运行条件,SoH和SoC也将有所不同[21 - 22]。这种不一致性将导致并联储能充放电过程中的“马太效应”。更具体地说,SoC最低的储能电池组最先耗尽,SoC最高的储能电池组最先充满电[23],这不仅导致储能系统容量的无效利用,但也使SoC较低的电池保持在高放电深度(depth of discharging,DoD)循环中[24]。退役电池劣化速度加剧,系统运行寿命和效率进一步降低。因此,根据各退役电池储能组的充放电特性,采用协调控制策略,确保SoH逐渐趋于一致,直到储能组停运退役。针对由普通蓄电池组成的储能系统的协调控制,已有一些研究成果。文献[25]提出了一种基于分布式多智能体共识的控制算法,以实现SoC轨迹跟踪控制、经济负荷分配、有功和无功功率共享控制以及电压和频率调节作用。文献[26]提出了一种基于SoC的分散下垂控制方法,实现了比例负载功率共享。这样,SoC越高的电池提供的负载功率越大,SoC越低的电池提供的负载功率越小[27]。然而,在上述控制方法中,未考虑由退役电池构成的储能组所具有的特性。
因此,本文提出了一种适用于直流配电网的多退役电池组并联的新型拓扑结构及其控制方法。这种拓扑结构有利于多退役电池储能组能够通过电池重组和协调控制实现单个退役电池的优化运行,以及退役电池储能组之间的协调运行。通过一致性算法获取全局退役电池SoH,调整各个储能组中退役电池的投切开关。同时,基于二次电压恢复控制。根据工作退役电池的SoC分布,调整储能器组中DC/DC变换器的下垂系数,从而实现储能组之间退役电池SoC的一致性,并优化组内退役电池的SoH。
1 多退役电池储能组并联运行系统拓扑
本文研究的新型多并联退役电池储能组拓扑结构如图1所示,每个储能组通过双向DC/DC变换器连接到直流配电网,多个储能组可以同时并联运行。

图1 多退役电池的储能组并联的拓扑Fig.1 Topology of parallel energy storage banks with multiple retired batteries
该拓扑结构具有以下优点。
1)利用率高。该拓扑兼顾储能组中每个蓄电池特性的差异(包括电压、容量、SoH和SoC),退役电池可以根据需要通过断路器K连接至储能组,避免了“马太效应”造成的容量浪费。
2)转换效率高。在该拓扑中,多个退役电池串联形成能量存储组,由于每个储能组中只有一个DC/DC电源转换器,因此转换效率高于为每个退役电池配备DC/DC转换器的拓扑结构。
3)兼容性强。即使每个回收电池的终端电压不同,回收电池也可以通过串联在直流母线上并联运行。也就是说,可以混合使用性能和容量不同的回收电池。
4)结构简单。每个DC/DC转换器的占空比可通过控制系统进行调整,以确保从储能组到直流母线的电压输出基本相同,从而基本上消除了组间的循环电流,而不依赖于复杂的蓄电池管理系统。
当配备有多个退役电池储能组的直流配电网系统运行时,直流配电网通常向本地负载供电,储能电池组可根据调度中心的指令实现电力稳定。另一方面,储能系统还可以根据直流母线电压自动输出或吸收功率,当直流配电网发生故障时,配电网断路器断开,储能组可在应急电源模式下运行,为本地负荷提供应急电源。
2 多退役电池储能组并联运行下直流配电网下垂特性分析
在直流配电系统中,通常对储能设备采用基于电压外环和电流内环的下垂控制方法。不同容量的储能组可以根据下垂系数自动按比例分配输出或吸收功率,并将直流母线电压保持在一定范围内,具有控制简单,无需通信的优点。
本文对各储能组的DC/DC变换器采用下垂控制,如式(1)所示。
VDC,ref=VDC,0+mPES
(1)
式中:PES为储能组的输出/吸收功率;m<0, 为下垂控制系数;VDC,0为直流母线电压的额定值;VDC,ref为储能组DC/DC电压控制环参考电压。
在多个储能组并联运行下,以两个为例进行分析,在采用(1)所示的下垂控制方法下,则有:
VDC,1=VDC,0+m1PES,1
(2)
VDC,2=VDC,0+m2PES,2
(3)
考虑直流配电网中各个储能组之间存在线路电阻的情况下,式(2)—(3)可改写为如下形式。
(4)
(5)
式中:Rline,1和Rline,2分别为储能组1和储能组2和直流配电网母线的之间的线路电阻。
由并联运行可得VDC,1=VDC,2,因此两个储能组之间具有式(6)所示关系。
(6)
因此,采用下垂控制的多个储能组并联运行下的直流配电网存在以下局限性。
1)功率分配精度受到线路电阻影响,功率分配比值由m1/m2=PES,2/PES,1变为式(6),其功率分配精度下降;
2)直流配电网母线电压降落由m1PES1变为m1PES1+m1Rline1/VDC,0,其电压降落增大。
3 多退役电池储能组协调控制方法
3.1 基于离散一致性算法的二次电压恢复
为了消除多组储能电池系统中组与组之间存在的线路电阻和下垂控制本身造成的电压偏差,本文基于平均电压偏差设计了一个电压二次恢复控制器。令xi代表退役电池i的状态变量,退役电池只与其邻居节点通信,当且仅当所有退役电池的状态变量相同时,系统达到一致收敛。其算法为[28]:
(7)
式中:ui(t)为退役电池i的输入变量,由邻居退役电池根据通信反馈决定,即为:
(8)
式中aij为退役电池连接图的邻接矩阵元素。
然而在实际的应用中,由于数据在计算、采样、传输以及控制过程中均需要时间。因此,连续的时间不再使用。将时间进行离散化,得到离散一致性算法为:
(9)
式中:dij为系统状态转移矩阵参数;k为数组索引。
当dij构造成的矩阵为双随机矩阵时,xi一致收敛于系统某一均衡点。该均衡点与系统初值相关,可由式(10)描述。
(10)
一致性算法的收敛速度取决于dij构造的系统状态转移矩阵D矩阵的本质谱半径ρ(D), 定义为:
Esr(D)=max{|λ|,λ∈ρ(D)}
(11)
式中Esr(D)为状态转移矩阵D的第二大特征值。
本质谱半径的大小及结构决定了收敛的模式及速度。本文采用的dij构造方法如式(12)所示[29]。
(12)
本文提出的二次电压恢复控制方法在原有的储能组DC/DC下垂控制的基础上加入了平均电压偏差进行修正。DC/DC电压外环参考值计算方法如式(13)所示。
VDC,ref=VDC,0+mPES+ΔV[∞]
(13)
首先,定义储能组DC/DC输出电压差ΔV为:
ΔV=Vave-VDC
(14)
式中:Vave为直流配电网平均额定电压;Vave=VDC,0-ΔVave;ΔVave为本文自定义允许偏差值。
为了使得各个储能组的输出电压差最终能够收敛到系统平均电压偏差值,对每个储能电池组的DC/DC变换器设置同步时钟,该时钟能够产生一个周期脉冲,以次驱动储能组DC/DC输出电压差计算及电压信息一致迭代,从而达到恢复由下垂系数带来的直流配电网平均电压差。
因此,各储能电池组计算得到ΔV后,将该值作为初值,下一个时钟产生的周期脉冲作用下进行一致性迭代,迭代公式如式(15)所示。
(15)
经过若干次迭代后,每个储能组输出电压差将一致收敛于全网平均电压差ΔV[∞],其收敛判据为:
(16)
式中:M为迭代的次数,取值范围为1~5;ε为收敛阈值,数量级为10-2。
基于离散一致性算法的储能组二次电压恢复控制框图如图2所示。

图2 基于离散一致性算法的二次电压恢复控制拓扑Fig.2 Topology of voltage recovery control based on discrete consensus algorithm
DC/DC变换器为双向Buck-Boost变换器,外环为基于下垂控制的电压环,内环为电流环。外环参考值由式(13)得到,一致性迭代按照式(15)更新,由式(16)判断是否进行输入。DC/DC变换器的开关管Q1和Q2通过电流内环输出值进行脉冲宽度调制(pulse width modulation, PWM)。
3.2 基于全局退役电池SoH的投切控制
SoH是电池老化和衰减过程的一个重要指标。SoH主要受蓄电池电压、截止电压、温度、电流比等因素的影响。由于本文研究对象为基于退役电池的储能系统,因此有必要建立退役电池的衰减机制。
假设当蓄电池的初始SoH为100%,记录从100%衰减到80%的总循环数次数。根据该循环次数可得,电池相对于充电/放电循环数SoH满足主要函数关系为:
SOH=-kt+B
(17)
式中:k为拟合函数的斜率;t为蓄电池充电/放电循环次数;B为拟合函数的常数项。这些参数均可通过电池退役前的历史数据得到。
上述方法需要知道蓄电池的充放电循环次数,不适用于储能组的实时控制,因此,本文采用的SoH更新方式为:
取同一批供试品溶液各 10 μL,分别于1.4,1.5,1.6 mL/min流速下进样,测定的有关物质结果分别为0.05%,0.06%,0.06%;在流动相V(磷酸盐缓冲液):V(甲醇):V(四氢呋喃)分别为 575∶335∶90,587∶323∶90 与 600∶310∶90 的条件下进样,所测定的有关物质结果分别为0.07%,0.06%及0.06%;将色谱柱更换为DikmaInertsilC8(4.6 mm×75 mm,3 μm),测定的有关物质结果为0.05%。上述试验结果表明该方法的系统耐用性良好。
(18)
式中:ΔC为单次充放电下的容量变化量;ΔSOC为单次充放电下的SoC变化量;CN为额定容量。
各蓄电池组收集其组内的退役电池SoH,并计算得到自身组内退役电池的SoH平均值。该平均值通过建立的通信网络向其他储能组传输,从而获得全局退役电池平均SoH。储能组SoH平均值更新方式为:
(19)
经过若干次迭代后,每个储能组SoH将一致收敛于全局退役电池SoH平均值SOH,ave,其收敛判据为:
(20)
各储能组根据得到的SOH,ave对其组内的退役电池进重组,其投切方法为:
(21)
3.3 基于多储能组SoC的下垂系数实时调整
由于下垂特性下,功率分配比和下垂系数相关。因此,只要将下垂系数设置为与SoC相关参数,输出或吸收功率就可以与储能组的剩余容量成比例,实现充电情况下,SoC高的储能组吸收功率小;放电情况下,SoC高的储能组输出功率大。
SoC的估计方法有安培-小时积分法、卡尔曼滤波法、开路电压法和神经网络法。结合本文提出的控制方法,开路电压法可以更方便地估计退役电池的剩余容量。由于退役电池的参数不精确,需要重新测量开路电压(open circuit voltage,OCV),再根据OCV与SoC之间的关系来描述电池特性。根据等效模型电路,失效电池的端子电压满足式(22)所示关系。
Vbat=Voc±RoIbat
(22)
式中:Voc为退役电池在当前SoC下的开路电压;Ibat和Ro分别为电池的工作电流和内阻。
由于电池SoC与OCV之间存在非线性关系,通过数据拟合方法可以得到电池SoC与OCV之间的关系函数。本文采用7次多项式拟合,其形式为:
(23)
式中:a、b、c、d、e、f、g、h为拟合参数;SOC为电池的荷电状态。
根据拟合的非线性多项式函数,在已知电池内部充放电电阻的情况下,可根据退役电池的测得的开路电压估计其SoC。
因此,重组后的退役电池储能组的下垂系数为:
(24)
式中kc和kd分别为充电和放电下的系数。
3.4 所提协调控制方法流程图
协调控制方法的总体流程如图3所示。

图3 所提协调控制方法流程图Fig.3 Flow chart of proposed coordinated control method
1)步骤1:系统中每个退役电池储能组根据式(18)计算得到自身健康状态变量SoH;
2)步骤2:各个退役电池储能组根据式(19)获得系统中所有退役电池健康状态变量的平均值SOH,ave;
3)步骤3:比较SOH和SOH,ave,选择大于平均值的退役电池进行工作,控制对应的断路器K将其放入储能组;
4)步骤4:重组后的储能组根据式(23)计算投入到储能电池组中退役电池的荷点状态SOC;
5)步骤5:根据式(24)设置DC/DC转换器的下垂系数与SoC成比例,使得储能组的充电功率和SoC成反比,和放电功率成正比;
6)步骤6:根据式(13)计算得到储能组DC/DC变换器电压外环参考值,使用PWM技术对其开关管进行控制。
4 所提协调控制方法稳定性分析
由于本文所提控制方法涉及分布式控制,而通信延时是影响分布式控制稳定性的重要因素。因此,将式(9)所示的离散一致性算法改写为含有通信延时的一致性迭代方程,即为:
(25)
式中τ为本文所假定的通信延时。
根据式(25)即可分析通信延时对所提控制策略的性能:根据τ的大小,其对控制策略性能的影响不同。如果通信延时τ小于时钟脉冲周期,控制策略性能不收影响。这是由于本文采用的离散控制决定的。
如果通信延时τ大于时钟脉冲周期,此时控制策略对系统的影响主要是由于一致性收敛效果带来的。若D的对角元素不全为0,则系统仍能收敛,控制策略性能不受影响。
一致收敛的性能由矩阵Z决定,可表示为:
(26)
式中:A为D的对角矩阵,F=D-A。
该矩阵对控制策略性能如下:若Esr(Z)对应的特征值为实数,则收敛速度呈指数;若Esr(Z)对应的特征值为共轭复数,则收敛速度按幅值衰减。本文采用的如式(12)所示的D,保证了对角元素不为0,且为双随机矩阵,因此所提控制策略可靠。
5 仿真分析
为验证所提出的协调控制方法的有效性,搭建直流配电网系统结构和平台如图4所示。图4所示的直流配电网系统有3组退役的电池储能组,每组由不同容量和端电压的退役电池通过开关K的控制串联而成。为了结合实际情况更清楚地验证所提出的协调控制方法的有效性,将各储能组作为一个独立的系统进行了仿真实验。所研究系统的初始工作条件和参数如表1所示。
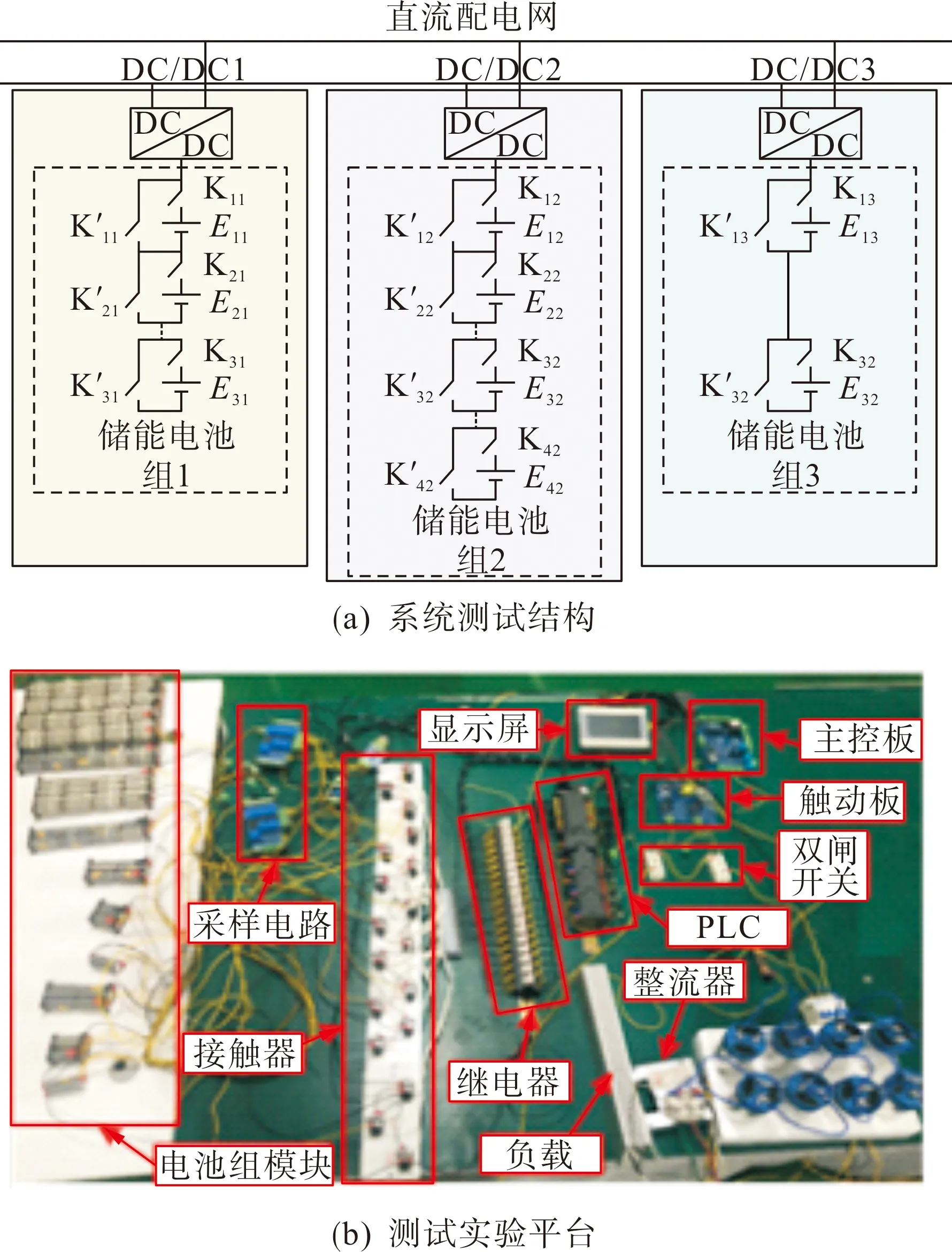
图4 测试系统的配置 Fig.4 Configuration of tested system

表1 退役电池储能电池组的参数Tab.1 Parameters of retired battery-based energy storage bank
在仿真实验验证中,直流配电网的额定直流电压为400 V,系统用电量按季节和工作日动态划分。春季单个工作日用电需求P设定为75 kW,非工作日用电需求P设定37.5 kW。夏季单个工作日用电需求P设定为100 kW,非工作日用电需求P设定为50 kW。秋冬两季单工作日用电需求P设定为50 kW,非工作日用电需求P设定为25 kW。不同季节的电力需求如图5所示。
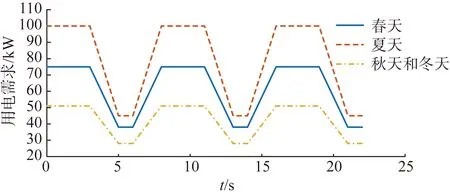
图5 不同季节的电力需求Fig.5 Electricity demand in different seasons
下文对春季运行结果进行了详细的分析和描述,阐述了所提出的协调控制方法的有效性。其他工况下的结果相似,本文不再重复。
5.1 直流电压波动性分析
首先,绘制了所研究系统中直流电压的运行结果,如图6所示。可以看出,在系统运行期间,由于所需功率的变化,在所提出的协调控制方法下,直流电压始终可以保持在稳定的范围内。根据直流配电网的标准要求,直流电压的波动范围约为额定电压的±5%。结果中显示的最大和最小直流电压波动分别为415 V和395 V,波动范围为-4%~4%。因此,可以认为,在所提出的协调控制方法下,被测系统能够稳定供电。
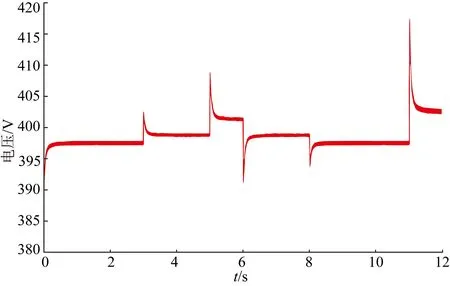
图6 直流电压测试结果Fig.6 Results of DC voltage test
5.2 充电/放电模式下功率切换
系统中每个退役电池储能组的功率运行结果如图7所示。
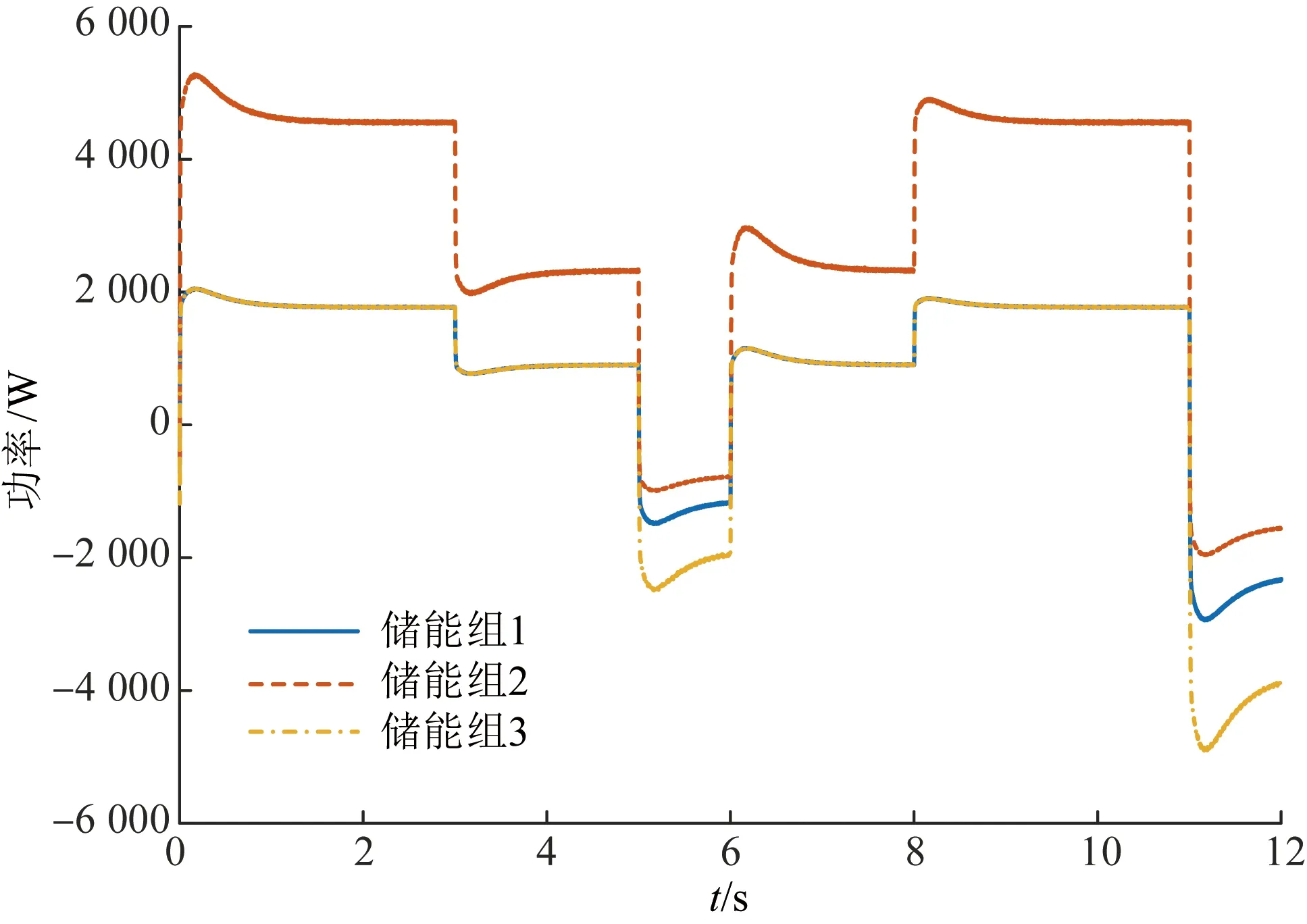
图7 基于退役电池的储能组电源充放电状态Fig.7 Charge and discharge state of retired battery-based energy storage bank power
结合图7,可知在系统运行期间,由于所需功率的变化,在所提出的协调控制方法下,储能组的放电/充电功率不同。这是因为DC/DC变换器采用的下垂控制,使储能器组能够根据系统的功率不足输出/输入相应的功率。同时,从图7可以看出,各储能组在充放电状态下的功率也不同,本文提出的协调控制方法能够根据蓄电池组中工作的退役电池的SoC进行功率分配。0~5 s内,储能系统工作在放电状态,在这种情况下,SoC较大的储能组将承受更多的负载功率。因此,储能组2在0~5 s承担了主要的电量输出,储能组1和3的输出功率基本相同。5 s后,系统从储能放电状态切换到充电状态。在这种情况下,SoC越大的储能组吸收的功率越小。储能组2由于剩余电量最多,SoC最高, 5 s后的充电功率最小。
5.3 SoH分析
最后,给出了系统中每个退役电池的SoH结果,如图8所示。通过根据SoC分配充电和放电功率,可以看出每个退役电池在运行期间的充电和放电功率是不同的。SoC越大的储能组在放电状态下输出的功率越大,而SoC越小的储能组只需要输出相对较小的功率。

图8 所有退役电池的SoH结果Fig.8 Results of all retired battery’s SoH
在使用所提出的协调控制方法时,系统将根据退役电池的SoH觉得其工作状态,所有退役电池的联合输出将切换为部分退役电池输出。结果表明,系统中所有退役电池的SoH渐近收敛到相同值,直到系统中所有退役电池的SoH一致,每个储能组的充电和放电都与SoC成比例。该系统将能够最大限度地发挥退役电池的经济效益,避免储能电池组过度充电和放电。
5.4 实验分析
由于受到实验条件的限制,本文仅对单组内退役电池的投切进行了实验验证,多组退役电池储能系统的投切同理。基于图4(b)的测试实验平台,对表1中储能组1进行了投切实验测试。图9所示为储能组1的充放电实验结果图。图9(a)为充电情况下退役电池投切波形,图9(b)为放电情况下退役电池的投切结果。

图9 储能组放电实验结果Fig.9 Experiment results of charging/discharging condition
图9(a)中储能组1首先由退役电池E31投入进行工作,在T0时刻投入了退役电池E21,此时E21开关两端电压由0上升为48 V,且开关状态由K21=0,K′21=1改变为K21=1,K′21=0。图9(b)中储能组1首先由退役电池E21和E31共同投入工作,在t0时刻增加了退役电池E11的投入,此时E11开关两端电压由0上升为110 V,且开关状态由K11=0,K′11=1改变为K11=1,K′11=0。同理,本文依次对储能组2和储能组3进行了相同的实验测试。
实验结果表明,不同开关短时切换下退役电池组在充电、放电模式下端电压都介于较小的变化范围,表明其电压端特性都比较稳定可控,也间接验证了所提下垂系数调整模式下协调控制策略的有效性。
6 结论
针对退役电池SoH不一致的问题,本文提出了一种应用于直流配电网的退役电池储能组的并联拓扑结构及其控制方法,可以实现直流配电网中多个退役电池储能组的协同运行,并通过控制退役电池的运行状态来优化退役电池的性能。经实验分析,验证了所提控制策略的可行性和有效性。
1)采用基于离散一致性的二次电压恢复控制解决了由下垂控制和线路电阻引起的母线电压偏差。
2)采用离散一致性算法获得全局退役电池平均SoH,选择SoH良好的单个退役电池投入储能组中优先输出,实现了全局退役电池SoH优化。
3)基于工作中的退役电池SoC,实时调整储能组下垂控制系数,分配储能组之间的功率,实现了退役电池SoC一致性。
关于不同通信拓扑结构及设计模式对所提控制方法性能的影响,将在下一步的工作中重点研究。

