基于改进强度Pareto进化算法的居民用户侧源储荷协调优化
冯浩洋,陈明丽,潘峰,杨雨瑶,马键
(1. 广东电网有限责任公司计量中心,广东 清远511547;2. 智慧能源工程技术研究中心,华南理工大学电力学院,广州510640)
0 引言
为了解决过去大量消耗化石能源所带来的环境污染和能源枯竭问题,高效利用可再生能源促进能源结构转型已经成为世界所关注的热点[1]。我国在第十三届全国两会中提出,力争在2030年前实现“碳达峰”,在2060年前实现“碳中和”。在电网数字化转型的过程中,优化源网荷储多方资源[2]、引导用户参与需求侧响应[3]成为电力领域响应上述目标的主要措施。
居民侧用电量在社会总用电量中占比较大,但是过去该领域用电效率低、浪费严重[4],近年来小型分布式光伏电源(distributed generation based on photovoltaic, DG Based on PV)和储能系统(energy storage system, ESS)逐渐走进居民用户的生活[5],这不仅提高了可再生能源的利用率,而且可以利用储能设备的双向充放电特性平抑负荷曲线的峰谷差[6]。在智能电网日渐成熟的环境下,随着智能家居的普及,居民用户侧负荷变得越来越复杂,并且尖峰负荷不断提高,潜在的过负荷危险威胁到了用户的日常用电[7 - 8]。但是相比于传统的居民侧负荷,智能家居提供了更多的调控手段,使得居民用户可以通过家庭能源管理系统(home energy management system, HEMS)参与需求侧响应,实现和电网的双向互动[9 - 10],所以如何协调优化源储荷资源是亟需解决的问题。
目前,对居民用户侧源储荷的协调优化理论研究中,一方面考虑对居民侧负荷的分类,另一方面考虑源储荷的协调优化模型。文献[11]将负荷分为刚性负荷、可中断类负荷、可调节负荷以及可转移负荷,以减少用户的用电成本安排需求侧响应策略。文献[12 - 13]更具体地针对电池类设备和供暖、通风和空调(heating, ventilation and air conditioning, HVAC)设备进行优化。文献[14]同时考虑了提高清洁能源消纳量,只针对可平移负荷和温控负荷进行优化。文献[15]从功率和时间的角度出发,建立了功率可调负荷模型、时间可调负荷模型和电动汽车负荷模型,以最小化用电费用和功率波动为目标函数求得优化策略。文献[16]以用电费用最小和净负荷曲线平坦度最优为目标规划可中断负荷的需求响应策略。上述文献在协调优化模型方面,仍以电网侧利益为主,在用户侧只考虑了用电费用,并未考虑到用户对电能质量和用电可靠性的要求,而这也是影响居民用户日常生活用电的关键因素[17 - 18]。
在求解多目标优化问题时,文献[19]采用加权和的方法将其转化为单目标优化问题,所得到的优化策略受权重系数的影响较大。文献[20]采用商业软件进行求解,未能根据模型特点做出改进。基于种群特性的多目标进化算法(multi-objective evolutionary algorithms, MOEAs)已被证明是最有效的途径[20],其中的强度帕累托进化算法(strength Pareto evolutionary algorithm2, SPEA2)在求解三目标优化问题时具有良好的收敛速度和分布性[22 - 23],但在求解不同问题时仍需根据模型特点做出改进。
综上所述,为了综合考虑用电费用、电能质量和用电可靠性,本文提出了一种基于改进强度Pareto进化算法的居民用户侧源储荷协调优化方法。首先,建立用户侧储能系统模型,并根据负荷是否参与需求侧响应以及参与的方式,将其分为刚性负荷、可削减负荷、可平移负荷和电动汽车负荷;其次,以减少用电费用、降低电压偏差和缩短故障停电时长为目标,综合考虑功率平衡、储能荷电状态、柔性负荷的优化范围等约束条件,构建了在分时电价和需求侧响应机制下的多目标源储荷协调优化模型;然后,引入扩展中间交叉算子优化SPEA2算法的收敛速度,利用多目标模糊综合评价决策法,从改进强度帕累托进化算法(improved strength Pareto evolutionary algorithm, ISPEA)求得的Pareto最优解集中确定优化策略;最后,通过一个低压网络仿真算例验证了所提模型的有效性。
1 居民用户侧能量设备模型
1.1 储能设备模型
储能系统具有充电和放电两种工作状态,负荷需求量小时,对其进行充电从而把多余的能量存储下来;负荷需求量大时,它可以放电从而把存储的能量供应给负荷,以保证系统稳定运行。储能系统在智能电网中的电能流向如图1所示。

图1 储能系统的电能流向Fig.1 Power flow of ESS
通常用储能系统的荷电状态(state of charge, SOC)来描述其充放电过程,计算公式为:
SESS(t)=SESS,0+
(1)
式中:SESS(t)为第t个时间段蓄电池的荷电状态;SESS,0为蓄电池的初始荷电状态;PESS,c(j)为第j个时间段的充电功率;ηESS,c为蓄电池的充电效率;PESS,d(t)为第t个时间段的放电功率;ηESS,d为蓄电池的放电效率;EESS,n为蓄电池的额定容量;Δt为计算时刻距初始时刻的时间间隔,取1 h的整数倍;T为调度周期。
1.2 本地负荷模型
根据负荷是否参与需求侧响应,将本地负荷分为刚性负荷和柔性负荷。刚性负荷,是指正常情况下必须保证可靠持续的供电的负荷,例如照明电灯和笔记本电脑。柔性负荷是指可以参与需求侧响应且不会影响用户正常生活的负荷,例如扫地机器人和洗衣机。因此,协调安排柔性负荷的运行时间和运行功率是实现协调优化的重要措施之一。柔性负荷又根据负荷参与需求侧响应的方式分为可削减负荷和可平移负荷,而由于可平移负荷中的电动汽车负荷通过充电桩接入电网,故对其单独进行建模,并将其余的几类负荷统称为家用负荷。
1)可削减负荷
可削减负荷是指启动后可以中断,用电量可以进行调整的负荷,例如空调、热泵、加热器等。此类负荷对供电可靠性要求不是太苛刻,并且响应能力强,在电力供需紧张时对其进行削减,但是需要根据削减时间、停电损失等因素给予用户一定的经济补偿,并且对其削减负荷功率和削减时间都有严格的限制,由此建立可削减负荷的模型如式(2)—(4)所示。
0≤PInt(t)≤PInt,max(t)
(2)
0≤ΔTInt(t)≤ΔTInt,max(t)
(3)
fInt(t)=CCom×PInt(t)×ΔTInt(t)
(4)
式中:PInt(t)为t时刻削减负荷功率;PInt,max(t)为最大削减负荷功率允许值;ΔTInt(t)为t时刻削减时间;ΔTInt,max(t)为最大削减负荷时间允许值;CCom为单位电量单位时间内的削减补偿价格;fInt(t)为给用户的削减补偿收益。
2)可平移负荷
可平移负荷是指启动后不可中断直到完整运行一个运行周期为止,但启动时间较为灵活,响应周期内用电量固定并且工作功率特性不变的负荷,例如洗衣机、电饭锅、扫地机器人等。考虑到可平移负荷连续运行的特性,建立其模型如式(5)—(6)所示。
TTra=TTra0
(5)
PTra(ΔtTra+tTras)=PTra(ΔtTra+tTras0)
(6)
式中:TTra为可平移负荷优化后的运行周期;TTra0为可平移负荷的原始工作周期;PTra(ΔtTra+tTras)为可平移负荷优化后任意时刻的工作功率;PTra(ΔtTra+tTras0)为可平移负荷在原始工作周期的相应时刻的工作功率。
3)电动汽车负荷
随着国家对电动汽车的大力推广,越来越多的居民用户选择电动汽车作为出行工具,并且主要是为了满足通勤需求。电动汽车作为特殊的可平移负荷,其响应时间固定并且通过充电桩接入电网。由于居民用户的电动汽车负荷响应时间长,所以本文选择充电功率低、充电时间长,但是充电费用低的交流慢充模式,利用电动汽车的荷电状态来描述其充放电过程,计算公式为:
(7)
式中:SEV(t)为t时刻电动汽车的荷电状态;PEV(t)为t时刻电动汽车的充电功率;ηEV为电动汽车的充电效率;EEV为电动汽车的电池容量。
2 多目标源储荷协调优化模型
2.1 目标函数
在低压网络中,用户负荷集中在高峰时段会使得用电费用较高,并且负荷曲线峰值过高容易造成线路过载,这不仅会导致用电电压偏低影响电能质量,严重时还会出现跳闸断电的可能。因此,本文综合考虑用户侧的用电费用、电能质量和用电可靠性,建立了以减少用电费用、降低电压偏差和缩短故障停电时长为目标的源储荷协调优化模型。
1)减少用电费用
在“自发自用,余量上网”的模式下,通过合理安排智能家用电器在可接受的范围内运行和在不影响用户生活的前提下对负荷进行削减,减少居民用户的用电费用,具体表现为减少用户的购电费用CL(t)、 余量上网收益CSell(t)、 削减补偿收益fCut(t)之和,即:
(8)
购电费用为:
(9)
PNet(t)=-(PPV(t)-PESS(t)-PL(t))
(10)
PESS(t)=PESS,c(t)+PESS,d(t)
(11)
PL(t)=PRigid(t)+PInt(t)+PTra(t)+PEV(t)
(12)
式中:c0(t)为t时刻的购电电价,元/kWh;PNet(t)为t时刻的净负荷;PPV(t)为t时刻分布式光伏电源发出的功率;PESS(t)为t时刻储能系统的功率;PL(t)为t时刻用户侧本地负荷;PUnsch(t)为t时刻刚性负荷的功率;
余量上网收益为:
(13)
式中cSell为余量上网电价,元/(kWh)。
2)降低电压偏差
由于家用负荷电压与用户日常生活质量息息相关,所以提高电能质量具体表现为降低一个优化周期之内家用负荷的实际电压偏离额定电压的最大值,即:
f2=min(max|V(t)-VN|),t=1,…,T
(14)
式中:V(t)为t时刻用户的实际电压;VN为额定电压;T为一个优化周期。
3)缩短故障停电时长
在台区发生停电故障的时候,通过协调储能系统的充放电和负荷的运行,缩短智能家庭用户家用电器的停电时长。
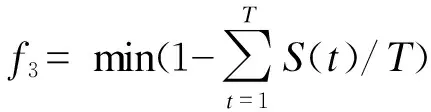
(15)
式中:PPV(t)为t时刻的光伏功率;PESS(t)为t时刻的储能设备的功率;PUnsch(t)为t时刻的刚性负荷;PCut(t)为t时刻的可削减负荷;PTra(t)为t时刻的可平移负荷。
2.2 约束条件
所构建的多目标源储荷协调优化模型在求解优化策略时需要满足以下的约束。
1)功率平衡约束
(16)

2)分布式光伏电源输出功率约束
PPV,min≤PPV(t)≤PPV,max
(17)
式中PPV,max、PPV,min分别为分布式光伏电源出力的最大值和最小值。
3)储能充放电功率限制约束
(18)
式中:PESS,max为蓄电池最大充放电功率;SESS,max、SESS,min分别为蓄电池所允许的荷电状态最大值和最小值。
4)储能充放电状态约束
储能设备在任意工作时刻只能处于充电状态或者放电状态,即:
PESS,c(t)PESS,d(t)=0
(19)
5)储能充放电平衡约束
一个调度周期内储能的充电功率和放电功率应相等,即:
由中国建筑材料检验认证中心、国家水泥质量监督检验中心编著的《水泥实验室工作手册》,已由中国建材工业出版社出版。该《手册》增补了近年来制定和修订的有关水泥产品和检验方法的新标准,同时增列了国家有关标准法和计量法的内容,对不符合国家计量法的一些表示方法进行了纠正。
(20)
6)可削减负荷削减功率和削减时间的约束
(21)
式中:PCut,max为最大削减负荷功率允许值;ΔTCut(t)为t时刻削减时间;ΔTCut,max为最大削减负荷时间允许值。
7)电动汽车充电约束
SEV,min≤SEV(t)≤SEV,max
(22)
式中SEV,max、SEV,min分别为电动汽车电池所允许的荷电状态最大值和最小值。
8)三相不平衡度约束
三相不平衡度(voltage unbalance factor, VUF)是低压网络运行的重要指标,通常利用电压的负序分量与正序分量的比值计算,即:
(23)
式中:VNeg,b(t)、VPos,b(t)分别为t时刻母线b的负序电压、正序电压;Va,b(t)、Vb,b(t)、Vc,b(t)分别为t时刻母线b上三相所对应的电压;α=1∠120°。
根据规定[24],电网正常运行时电力系统公共连接点电压不平衡度允许值为2%,即:
UVUF,b(t)≤2%
(24)
Vmin≤Vi(t)≤Vmax
(25)
式中Vmax、Vmin分别为节点电压的最大值和最小值。
3 基于ISPEA和多目标模糊综合评价决策法的优化求解策略
SPEA2算法是由Zitzler等[23]于2001年在SPEA算法的基础上进行改进获得的,非常适合求解多目标、多约束和非线性的优化问题,尤其是当有3个相互矛盾的目标函数时,其相比于其他多目标进化算法,能保证良好的Pareto最优解的分布性。由于居民区用电网络节点较多,所以计算电压较为复杂,为了进一步提升算法的收敛速度,本文在SPEA2算法的基础上,提出引入扩展中间交叉算子简化交叉变异过程、加快父代种群交配过程的ISPEA算法,并和多目标模糊综合评价决策法结合确定优化策略。
根据前文分析,本文以减少用电费用、降低电压偏差和缩短故障停电时长作为优化目标,将储能系统的充放电功率、可削减负荷的削减时间及削减功率、可平移负荷的起始运行时间、电动汽车负荷的起始充电时间作为决策变量,ISPEA计算流程如图2所示,具体的实施步骤描述如下。

图2 ISPEA计算流程Fig.2 The flow of ISPEA
步骤1:读入预测的光伏电源输出功率PPV(t)、柔性负荷的功率、决策变量的约束值、分时电价信息、用电网络参数;
步骤2:根据约束条件随机创建决策变量的初始值形成初始种群P0,同时创建空的外部档案A0,设置t=0 ;
步骤3:计算种群Pt和外部档案At中个体的用电费用、电压偏差和故障停电时长,根据Pareto支配关系计算强度值和适应度值;
步骤4:按适应度值小原则对个体排序,并选择非支配个体复制到At+1中,若At+1超出存档规模,则实行剪枝操作;
步骤5:终止判断。若满足终止条件,则输出At+1为Pareto最优解集,否则,算法继续运行;
步骤6:选择操作。对At+1进行锦标赛选择,选择出的个体作为父代放入交配池;
步骤7:交叉变异。利用扩展中间交叉算子[25]和均匀变异算子[26]对交配池中的个体进行交叉和变异,生成子代种群;
步骤8:t=t+1,转到步骤3;
步骤9:利用多目标模糊综合评价决策法将个体的3个目标函数值进行归一化处理,将每个目标函数值归一化到区间[0,1]内,利用层次分析法赋予各子目标权重,求出平均满意度,Pareto最优解集中平均满意度最大的个体为优化策略,即:
(26)
(27)

4 算例分析
本文以一个75节点的0.4 kV的低压网络为例进行仿真分析,该低压网络的拓扑结构如图3所示。调度区间时长为1 d,均分为每1 h共24个时间段。该低压网络中一共12户居民,每一户都有家用负荷和电动汽车负荷,其中有A、B、C 3户居民有分布式光伏电源和储能设备,可以选择是否参加需求侧响应。

图3 低压网络的拓扑结构Fig.3 Topology of a low voltage distribution network
储能设备参数如表1所示。按照广州市交流慢充桩的充电功率7 kW对用户的电动汽车进行充电,假设用户结束电动汽车行程(回家)时的时间为当日17:00,开始电动汽车行程(离家)时的时间为次日08:00,即电动汽车负荷的响应时间为当日17:00到次日08:00,在优化前用户选择刚回到家就给电动汽车充电,即17:00接入电动汽车负荷,电动汽车设备的相关参数如表2所示,其中,SEV,0、SEV,end分别为电动汽车开始充电和结束充电时的荷电状态。24 h内光伏电源的出力曲线和居民用户本地负荷曲线如图4所示[11]。
用户侧采用分时电价,具体不同时段的电价信息如表3所示。用户侧余量上网电价为0.673元/kWh,对可削减负荷的削减补偿电价为1.258元/kWh,最大削减负荷功率允许值为0.5 kW,最大削减负荷时间允许值为2 h。

表1 储能设备参数Tab.1 Parameters of ESS
利用本文所提出的ISPEA算法对用户B进行分析,并利用层次分析法对3个目标函数的权重赋值为ω1=0.63,ω2=0.28,ω3=0.09,按照用户A、C是否参加需求侧响应对4类场景进行仿真分析。

表2 电动汽车参数Tab.2 Parameters of EV
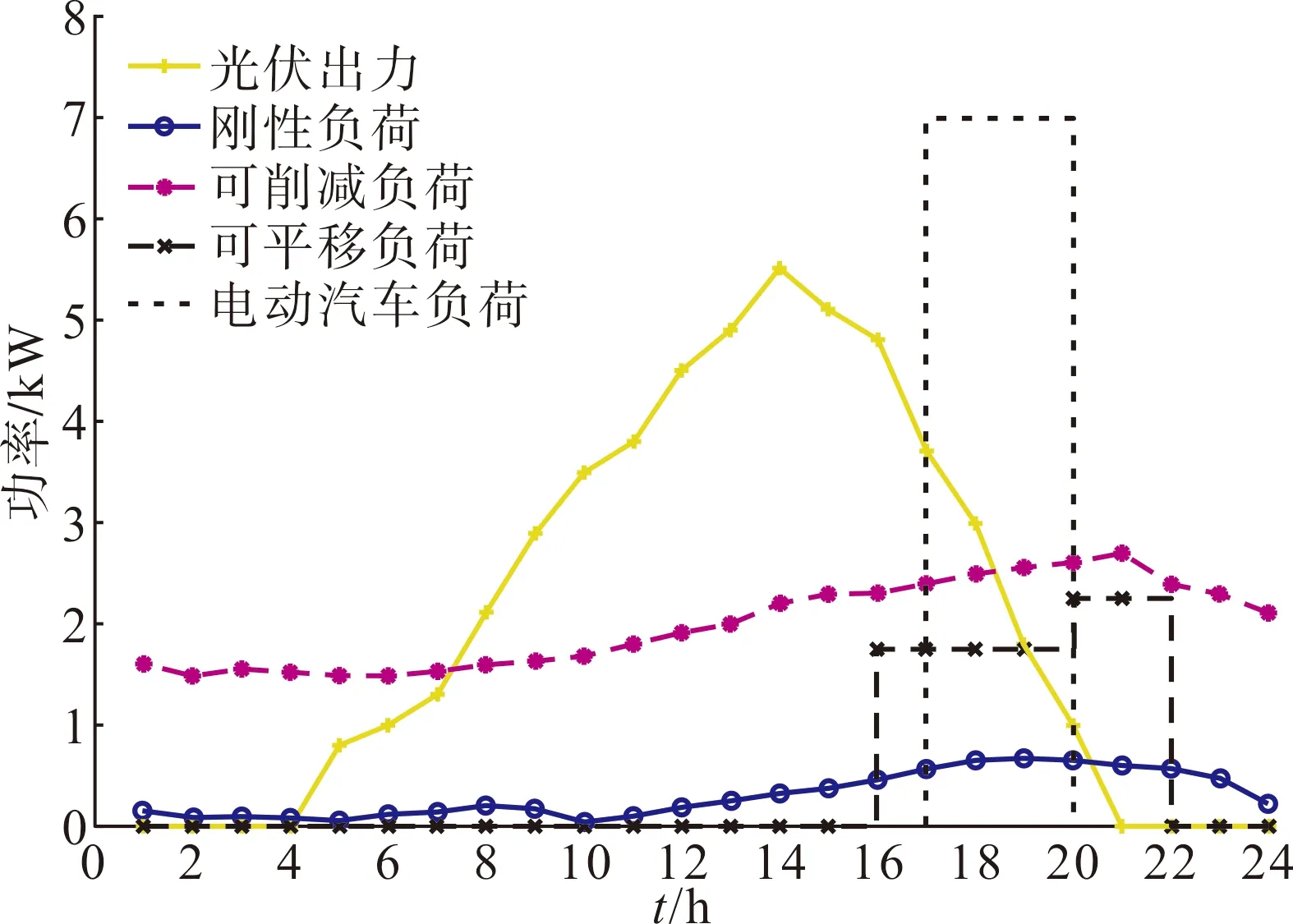
图4 光伏出力曲线和本地负荷曲线Fig.4 PV output power curves and domestic load curves
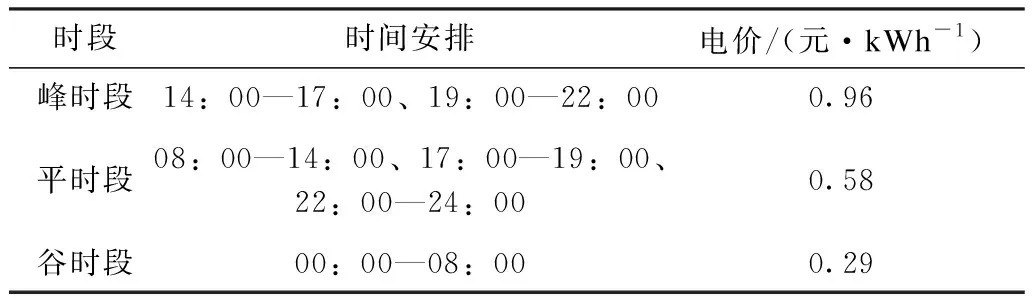
表3 分时电价Tab.3 Time-of-use price
4类场景下的优化策略相同,如表4所示,优化前后的本地负荷曲线如图5所示,优化后储能设备的荷电状态和充放电功率曲线如图6所示,4类场景下的目标函数值如表5所示。

表4 调度策略Tab.4 Scheduling strategy

图5 优化前后的本地负荷曲线Fig.5 Local load curves before and after optimization

图6 储能荷电状态和功率曲线Fig.6 SOC and power curves of ESS

表5 不同场景下的目标函数值Tab.5 Objective function values in different scenarios
用本文所提出的方法优化源储荷三方资源后,从图5可以看出,用户B 的本地负荷曲线的峰谷差明显减小,缓解了用户高峰时段用电紧张的问题;从表5可以看出,任一场景下都有明显的优化效果,用电费用减少44.49%;在这种运行策略下,如果电网侧发生意外停电,则用户家用负荷在24 h内的停电时长将缩短3 h,由图5及图6可知,此时家用电器在16:00—19:00能继续正常用电;而需求响应的参与度会影响用户的电能质量,需求响应参与度越高,用户的电能质量越好,其家用负荷电压偏差最大可降低45.41%,显著提升了用户的电能质量。
为了直观展示本文所提的ISPEA算法的优越性,将其与SPEA2算法进行对比。对只有用户B参与需求侧响应的场景一进行分析,结果显示两者最终求得的优化策略相同,但是在求解用时方面,ISPEA算法的求解速度比SPEA2算法快76.71%,如表6所示。

表6 算法用时对比Tab.6 Comparison of algorithm time
为了进一步验证本文所提方法的有效性,对不同协调优化目标下的用电费用、电压偏差、故障停电时长和本地负荷曲线的最小负荷系数Pmin/Pmax进行对比,结果如表7所示。
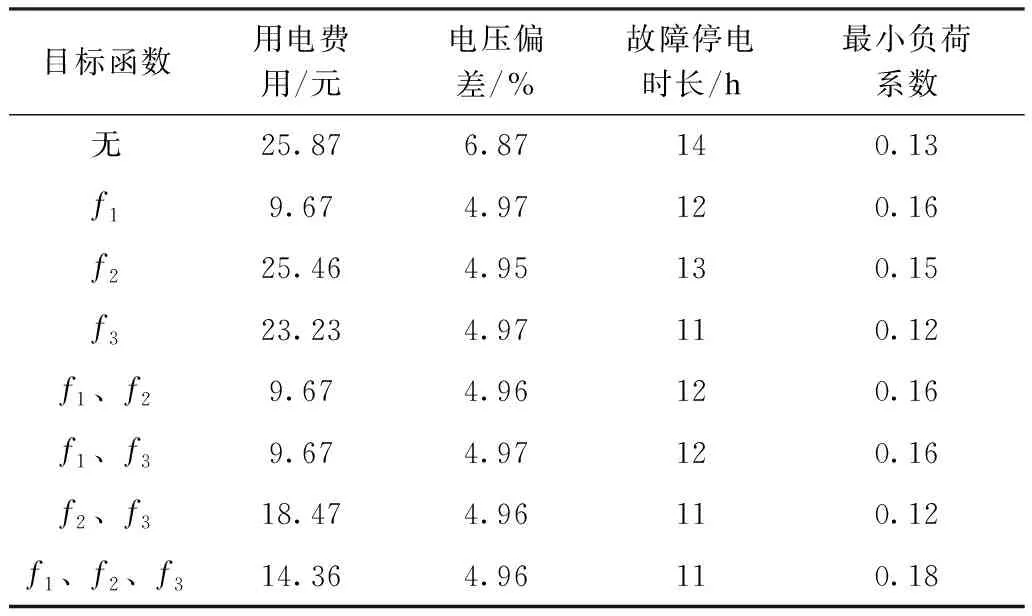
表7 不同优化目标下的结果Tab.7 Results under different optimization objectives
从表7可以看出,当协调优化模型只考虑单一子目标时,该子目标将获得最好的优化效果,但是其他目标的优化效果较差,并且最小负荷系数都较小,说明本地负荷曲线的波动性仍较大,并没有充分发挥储能系统削峰填谷的作用,仍会给电力系统的运行带来不稳定因素;当协调优化模型考虑两个子目标时,会结合两个子目标的权重系数折中选取最终策略,但是另一个子目标的优化效果不佳,并且最终得到的本地负荷曲线波动性也较大;当协调优化模型考虑3个子目标时,会折中选取最终策略尽量使得3个目标都靠近最优解,并且最终得到的最小负荷系数最大,说明此时负荷曲线的波动最小,充分发挥了储能系统削峰填谷的作用,证明了本文所提模型的有效性。
4 结论
为了减少用电费用、提高电能质量和用电可靠性,在分时电价和需求侧响应机制下,本文提出了一种基于改进强度Pareto进化算法的居民用户侧源储荷协调优化方法。以减少用电费用、降低电压偏差和缩短故障停电时长为目标,以ISPEA和多目标模糊综合评价决策法确定优化策略,分析低压网络中不同场景下的优化效果和计算效率。得到以下结论:
1)所提出的多目标源储荷协调优化模型能够明显减少居民用户的用电费用、降低电压偏差和缩短故障停电时长,提高电能质量和用电可靠性;
2)所提出的改进强度Pareto进化算法不仅加快了模型的求解速度,而且保证了在分时电价和需求侧响应机制下得到的优化策略的有效性;
3)所求得的优化策略适用于低压网络,且能够充分发挥储能系统削峰填谷的作用,平抑负荷曲线的峰谷差;
4)所得到的优化策略不仅考虑了用户侧的利益和用电体验,并且能够为调度人员提供决策参考。

