计及SOFC余热回收的氢-冰储能典型园区微网优化配置模型

项鹏飞，葛磊蛟，周震震，刘航旭，陈伟

(1.中国南方电网有限责任公司直流输电设备状态评估与故障诊断实验室，广州 510663；2. 天津大学智能电网教育部重点实验室，天津300072)

0 引言

国家“十四五”能源规划已明确：以多能互补为重点促进传统能源结构转型，发展风电、光伏、氢能等新能源技术解决环境污染、能源短缺的问题。然而，风/光发电具有强随机性和间歇性[1]，直接规模化并网给电力系统运行带来电压、频率等挑战[2]；氢能能量密度大，兼顾电力储能属性[3]；冰蓄冷作为相变储能的重要技术之一，可有效实现电网削峰填谷，因此，以氢储能、冰蓄冷、风/光新能源为核心构建多能互补交直流微网，能够实现绿色清洁高效能源利用。进一步，针对目前氢燃料电池的能量利用率较低，传统交流微网中交直流源-荷电能变换的能量损耗显著，设计计及固体氧化物燃料电池(solid oxide fuel cell，SOFC)余热回收的风-光-氢-冷多能互补的交直流混联微网，将会使系统能效进一步提升，值得深入研究[4]。

交直流混联电网充分考虑交直流不同类型负荷的特点[5]，减少电能变换环节，能有效提升能量利用率，成为了当今电力系统的重要组成部分之一[6]。文献[2]研究了基于风/光/柴/储的孤立微网的可靠性，其中储能选用铅酸蓄电池。文献[7]提出了基于风/光发电的交直流混联配电网，其中储能依然是锂电池。简言之，现有的交直流混联电网中，储能以铅酸或者锂电池为主，将导致后续储能的运营费用偏高，蓄电池寿命到期后也可能会污染坏境[8]。

为了解决传统储能装置费用高而污染环境的难题，电转气、氢储能、冰蓄冷等相变储能成为近年来储能技术的一个重要发展方向。文献[9]考虑光伏出力不确定性提出了对氢储能接入配电网的有功-无功功率协调控制策略。文献[10]对含有热储能的综合能源系统进行了多目标协同优化。文献[11]为提高能源系统运营商收益水平，结合氢储能多能联供联储的优点，设计由运营商配置氢储能的工业园区综合能源系统基本架构。文献[12]提出了可再生能源发电-氢生产及储能联合系统，以制氢成本最低为目标对可再生能源制氢系统的优化配置进行了较为全面的研究。文献[13]建立了分布式光伏能源驱动制冰蓄冷系统的光-电能量特性理论模型。文献[14]提出含冰蓄冷空调的CCHP-MG多时间尺度优化调度模型，研究了冰蓄冷空调的不同运行方式对优化调度的影响。

简言之，现有针对清洁储能方式的研究主要采用电转气、氢储能或冰蓄冷储能，较少同时利用两种及以上的储能技术。尤其是面向电/氢/冷等多种能源需求的典型园区，以可再生风光能源为基础，同时结合冰蓄冷与氢储能技术更加有利于能效水平进一步提升，建设灵活、坚强、可靠、智能的能源互联网[15]。

为此，本文结合之前的研究成果，针对传统多能互补交流微网中交直流电能变换的能量损耗大的问题，提出交直流混联的微网架构；面向风/光新能源高比例消纳，提出氢储能-冰蓄冷双重储能机制，相比于单一的氢储能和冰蓄冷可以更充分消纳风能、太阳能等可再生能源；同时为了氢能的能效水平进一步提升，提出SOFC的余热回收进行冷-电联产。进一步，针对系统目标函数及约束条件的非线性，风/光电源-储能系统-负荷等系统拓扑结构复杂、运行状态多变、双向解耦困难，容量优化配置难以全局寻优的问题，提出人工蜂群-量子粒子群算法(artificial bee colony-quantum particle swarm optimization，ABC-QPSO)对模型进行求解，实现了源-储容量优化，以期为我国风/光资源高效利用以及传统能源转型提供思路。

1 多能互补交直流混联微网结构与数学模型

1.1 系统拓扑架构

考虑到典型园区用户电、冷、氢等多种能源需求和高温燃料电池的余热回收价值，计及SOFC余热回收的技术先进性，构建氢-冰储能典型园区多能互补交直流混联微网系统，拓扑结构如图1所示。

图1 多能互补交直流混联微网结构图Fig.1 Structure diagram of multi-energy complementary AC/DC hybrid microgrid

包含风力发电机(wind turbine，WT)、光伏电池(photovoltaic，PV)、碱性电解槽(alkaline electrolysis cell，AEC)、储氢罐(hydrogen storage，HS)、制冰空调、蓄冰罐(cold storage，CS)、固体氧化物燃料电池(solid oxide fuel cell，SOFC)、微型燃气轮机(micro gas turbine，MGT)、溴化锂吸收式制冷机(lithium bromide refrigerator，LBR)。其中，交流侧包含WT、交流负荷、制冰空调和MGT；直流侧包含PV、直流负荷、AEC以及SOFC；为了保证交直流侧负荷的可靠供给，分别用储氢罐和蓄冰罐贮存氢气和冰，多余的氢气供给到用氢负荷；当风光电源出力不足时，蓄冰罐进行融冰释冷满足冷负荷需求，SOFC消耗储存于储氢罐的氢气进行发电，由于SOFC无法完全实现对氢气的完全利用，且工作温度较高(800～1 000 ℃)，产生的高温废气依旧含有较多的氢气和热能，可以将其导入MGT进行发电，MGT的低温废气再通过LBR的余热回收器进行制冷，实现能量的梯级利用，能量综合利用率可达到90%以上。下面对交直流混联微网系统中每一个组成单元的模型进行详细介绍。

1.2 数学模型

1.2.1 风力发电机

风力发电机组输出的功率与轮毂处的风速关系可以用式(1)的分段函数近似表示[16]。

(1)

式中：PWT为风力发电机的输出功率；Pr为额定功率；v为风电场风速；vout为切出风速；vin为切入风速；vr为额定风速。

1.2.2 光伏电池

光伏系统的输出主要受太阳辐射的影响，光伏输出可表示为[17]：

(2)

式中：G为太阳辐射强度；PSTG为光伏电池最大功率；l为功率温度系数；ta为环境温度；tNOC为元件额定工作温度。

1.2.3 碱性电解槽说

文中所用的电解槽模型溶液浓度为30%的KOH碱性电解槽。在风光出力充足时，对电解槽输入PV产生的电能用来制氢，制氢速率可表示为：

(3)

式中：QAEC为电解槽的制氢速率，kg/s；PAEC-in为输入到电解槽的电功率；ηel为电解槽的能量转换效率，一般在65%～80%之间；HVH2为氢气的热值，为142 MJ/kg。

1.2.4 储氢罐

储氢罐用于储存电解产生的氢气。假设在微小时间间隔Δt内系统内各设备功率不变，当前存储的氢气量可表示为：

QHS(t)=QHS(t-Δt)+(Qin-Qout)Δt

(4)

式中：Qin为输入到储氢罐氢气流量；Qout为储氢罐输出的氢气流量；QHS(t)为储氢罐在t时刻储存的氢气量。设初始状态下储氢罐内储存的氢气达到最大量。

1.2.5 考虑余热回收的SOFC-MGT-LBR

SOFC的工作温度较高，其排气余热仍有回收利用的价值[18]，SOFC发电单元未反应的燃料可通入后燃室中进行利用从而驱动微型燃气轮机实现余热的高效梯级利用[19]。然而，微型燃气轮机的能量利用效率较低，排热占到输入能量的50%以上，将这部分热量用溴化锂吸收式机组进行回收用于产生冷水[20]。考虑到本文电-冷-氢需求的典型园区，本文结合两种余热回收方式，提出SOFC-MGT-LBR组合的冷电联产余热回收系统。在风光出力不足时，燃料电池启动消耗氢气弥补电力缺额，产生的含氢气的高温一级废气进入MGT进行发电；MGT排出的低温二级废气通过传热管对溴化锂稀溶液加热从而制冷。

1)SOFC模型

SOFC是一种高温燃料电池，可以氢气为燃料输入到阳极，以空气为氧化剂输入到阴极，直接将化学能转化为电能[21]。其输出功率可表示为：

PSOFC=QSOFCUf1HVH2ηfc

(5)

式中：QSOFC为耗氢速率，kg/s；Uf1为燃料利用率；ηfc为能量转换效率。因此可得出SOFC单位时间内排出的一级废气中剩余能量。

Qout1=QSOFCHVH2(1-Uf1)-QSOFCHVH2Uf1(1-ηfc)

(6)

2)MGT

MGT接受SOFC产生的燃料未完全利用的高温废气，进入燃烧室驱动透平做功发电[22]。输出功率可表示为：

PMGT=Qout1ηMGTUf2

(7)

式中：ηMGT为MGT的能量转换效率；Uf2为MGT的燃料利用率。

排出的低温二级废气的余热可表示为：

(8)

3)溴化锂吸收式制冷机

溴化锂制冷机以水为制冷剂，溴化锂溶液为吸收剂，利用水的蒸发吸热完成制冷[23]，可利用低温热源作为余热回收的最后一级完成余热制冷。本文采用单效溴化锂吸收式制冷机制冷功率可表示为：

Pqc=Pout2ηhCqc

(9)

式中：ηh为溴化锂吸收式制冷机的余热回收率；Cqc为机组的制冷系数。

1.2.6 制冰空调

制冰空调平抑风电出力过大的时段，利用相变储能将多余的电转化为冰储存于蓄冰罐。制冷功率可表示为：

Pice=Pice-inCice

(10)

式中：Pice-in为制冰空调消耗的电功率；Cice为制冰空调的制冷系数。

1.2.7 蓄冰罐

当微网负荷处于高峰时期或制冷功率不足时，蓄冷池释冰输出冷量，由于蓄冰池存在冷损耗，释冷功率可表示[15]为：

CCS2=CCS1(1-θ)

(11)

式中：CCS2为实际供给到负荷侧的冷量；CCS1为蓄冰罐融冰释放的冷量；θ为冷量损耗系数。

蓄冰罐的蓄冰量表示如下：

QCS(t)=QCS(t-Δt)+(Pice+Pqc-CCS1(t))Δt

(12)

式中：QCS(t)为蓄冰罐在t时刻储存的冰量。设初始状态下储氢罐内储存的氢气达到最大量。

1.2.8 AC/DC转化模型

为了减少能量转换环节而提出交直流混联微网，但考虑到交、直流两侧电能的互联，利用双向AC/DC变化技术实现交流母线与直流母线的双向能量耦合[24]。系统会尽可能减少电能变换过程，交流负荷与制冰空调优先使用WT和MGT，直流负荷、电解槽优先使用PV和SOFC。电能变换过程可用如下公式表达：

PAC-DC=PACηAC-DC

(13)

PDC-AC=PDCηDC-AC

(14)

式中：PAC-DC、PDC-AC分别为从交流母线变换到直流母线的电功率和从直流母线变换到交流母线的电功率；PAC、PDC分别为交流母线向直流母线输送的电功率和交流母线向直流母线输送的电功率；ηAC-DC、ηDC-AC分别为交-直流变换效率和直-交流变换效率。

通过上述建模，可以获知各环节能量输入输出关系，然后根据系统运行特性，考虑园区的实际外部边界条件，可对每一个设备容量进行优化配置，从而实现能源高效利用。

2 优化模型

以提升交直流混联微网系统的经济性、可靠性为目标，针对电源/储能/负荷种类多样，充分考虑风/光电能出力的时空分布特性、氢储能双向解耦互动特性、冰蓄冷的能效特点、微网的运行成本等多时间尺度、多耦合特性和多不确定性，设计氢-冰储能多能互补交直流混联微电网优化配置模型。

2.1 目标函数

多能互补交直流混联微网容量优化规划，综合考虑设备的投资建设成本和提供电、冷、氢服务获取的收益，从而获得最佳的经济利益。本文以总收益最大为目标函数，如式(15)所示。

maxC=Cins-y+CE+CH+CC-Cins

(15)

式中：Cins为设备的投资费用；CE、CH、CC分别为供电、供氢、供冷的收益；Cins-y为设备在第y年的残值。其中，Cins、Cins-y、CE、CH、CC可用式(16)—(20)表示。

Cins=CWTPr+CPVPSTG+CAECPAEC+
CHSFHS+CFCFFC+CMGTFMGT+
CqcFqc+CiceFice+CCSFCS

(16)

(17)

(18)

(19)

(20)

式(16)中：CWT、CPV、CAEC、CHS、CFC、CMGT、Cqc、Cice、CCS分别为WT、PV、AEC、储氢罐、SOFC、MGT、LBR、制冰空调、蓄冰罐的单位容量造价；Pr、PSTG、PAEC、FHS、FFC、FMGT、Fqc、Fice、FCS分别为WT、PV、AEC、储氢罐、SOFC、MGT、LBR、制冰空调、蓄冰罐的安装容量。式(17)中：设备残值计算采用平均折旧法；y为当前年份；Y为设备总寿命。式(18)—(20)中，Ce、Ch、Cc分别为提供电、氢、冷的单位收益；Pload,i、Hload,i、Cload,i分别为在第i小时的电、氢、冷负荷需求。

2.2 约束条件

2.2.1 设备约束

1)WT出力约束

WT的最大出力取决于切出风速和安装容量，约束条件为：

0≤PWT≤Pr

(21)

式中Pr为风机的最大容量。

2)PV出力约束

PV的最大出力取决于安装容量PSTG：

0≤PPV≤PSTG

(22)

式中PSTG为光伏电池的最大功率。

3)AEC最大输入功率约束

AEC可以消纳光伏出力，但受到安装容量的限制，可能存在多余的光电无法完全吸收的情况：

0≤PPV-AEC≤PAEC

(23)

式中PAEC为电解槽的最大输入功率。

4)储氢罐容量约束

储氢罐存在最大储氢容量，当储存的氢气量为0时存在出现负荷失电的概率。

0≤QHS≤FHS

(24)

式中FHS为储氢罐的最大容量。

5)SOFC出力约束

SOFC的最大出力约束条件如式(25)所示。

0≤PSOFC≤FFC

(25)

式中FFC为燃料电池的最大输出功率。

6)MGT出力约束

MGT吸收来自SOFC的一级废气，输出功率主要受到安装容量的限制。

0≤PMGT≤FMGT

(26)

式中FMGT为MGT的最大输出功率。

7)溴化锂制冷机制冷约束

溴化锂吸收式制冷机运行约束如式(27)所示。

0≤Pqc≤Fqc

(27)

式中Fqc为LBR的最大输出功率。

8)制冰空调运行约束

制冰空调运行约束如下：

0≤Pice-in≤Fice

(28)

式中Fiec为制冰空调的最大输出功率。

9)蓄冰罐约束

类似于储氢罐，蓄冰罐也存在最大储冰容量：

0≤QCS≤FCS

(29)

式中FCS为蓄冰罐的最大容量。

2.2.2 运行约束

1)电功率约束

PPV+PWT+PMGT+PSOFC=Pload+PAEC-in+Pice-in+Pdis

(30)

式中：Pdis为储能系统无法消纳而产生弃风弃光的电功率；PPV、PWT、PMGT、PSOFC分别为WT、PV、MGT、SOFC的输出功率；Pload、PAEC-in、Pice-in分别为电负荷、AEC输入功率、制冰空调输入功率。

2)氢流量约束

任一时刻，氢流量存在式(31)所示约束。

0≤QAEC+Qout-QSOFC-Qin≤Hload

(31)

式中：QAEC、Qout分别为电解槽、储氢罐的氢气输出流量；QSOFC、Qin分别为SOFC消耗的氢气流量和输送进储氢罐的氢气流量；Hload为氢气负荷的需求流量。

3)供冷约束

系统可供给的最大冷负荷取受到式(32)约束。

0≤Cqc+Cice+CCS2≤Cload

(32)

式中：Cqc、Cice、CCS2分别为LBR、制冰空调、蓄冰罐的输出冷量；Cload为冷负荷需求功率。

上述以年收益最大化为目标函数和以微网系统内各设备的合理运行范围为约束条件，构成了计及SOFC余热回收的氢-冰储能典型园区微网优化配置模型，下面针对模型进行求解。

3 求解算法

本文所构建的计及SOFC余热回收的氢-冰储能典型园区微网优化配置模型是一个含等式约束和不等式约束的混合整数非线性连续规划问题，尤其是其约束条件中表达电解槽、制冰空调工作状态的PPV-AEC、Pice-in与目标函数变量之间关系无法用解析表达式表征，且微网运行环境的多变，风/光电源、直流电解水制氢、交流供电冰蓄冷蓄冷以及微网的运行参数等的随机性和风光出力的非线性等，使得优化求解过程难以找到全局最优，传统的优化算法在求解过程容易早熟、陷入局部最优、收敛速度慢，因此提出全局搜索能力强、收敛速度快、鲁棒性强、带约束条件的混合人工蜂群和量子粒子群的(artificial bee colony-quantum particle swarm optimization，ABC-QPSO)算法。与已有的ABC-QPSO算法不同，本文提出的算法并不是在QPSO算法中增加了一个扰动项 (自适应人工蜂群变异算子)，而是在传统ABC算法的基础上，保留原有算法的种群内信息交换、群内分层重构的模式，在个体搜索的方式上采用QPSO算法，使个体的搜索环节带有寻优性，本质上是具有量子搜索特征的人工蜂群。本算法综合考虑ABC和QPSO算法的特点，以ABC算法为基础，保留了引领蜂返回蜂巢进行群内交换信息、低质量蜜源遗弃、蜂群结构动态变换等特点，在引领蜂、跟随蜂的搜索过程结合QPSO算法的位置更新思路进行了改进，在保持传统ABC算法全局搜索能力强的前提下克服了蜂群在蜜源附近搜索的单一随机性，提高蜜源附近的搜索速度从而快速收敛。具体过程如下。

1)初始化。输入WT、PV、AEC、储氢罐、SOFC、MGT、LBR、制冰空调、蓄冰罐9种待优化设备的边界条件，产生规模为S的种群。

2)引领蜂根据式(33)产生蜜源：

xid=Ld+rand(0,1)(Ud-Ld)

(33)

式中：xid为蜜源i(i=1,2,3,…,S)在d维的位置；Ud、Ld分别表示d维的上、下边界，蜜源在各维度位置表示对应的设备安装容量。

3)将引领蜂携带的安装方案输入到本文所提园区微网的仿真模型，根据式(15)计算年收益，以此输出蜜源的适应度，返回蜂巢共享蜜源信息。

4)跟随蜂根据引领蜂分析的蜜源信息，按式(34)计算概率并按照轮盘赌方式随机选择引领蜂跟随。

(34)

式中：fi为蜜源i的适应度；pi为跟随蜂跟随该蜜源的概率。

5)首次搜索时跟随蜂按照式(35)随机生成在蜜源附近的蜜源。

vid=xid+φ(xid-xjd)

(35)

式中：vid为引领蜂找到的蜜源位置，i≠j；φ为[-1,1]均匀分布的随机数，决定扰动程度。

6)在蜜源i对应的蜂群中，寻找当前蜜源附件蜂群的全局最优位置和个体最优位置。

7)根据式(36)计算个体最优平均位置。

(36)

式中：mpbest_i为个体最优平均位置；ppbest_i-k为本次迭代中蜜蜂i的蜂群中蜜蜂k个体最优位置。

8)引领蜂、跟随蜂按照式(37)更新位置。

(37)

式中：pi-k(t)和pi-k(t+1)分别为蜜源i附近蜂群中蜜蜂k在第t次和第t+1次迭代中的位置；μ为(0,1)上的随机数；式中符号μ取+和-的概率都是0.5：当μ>0.5时，取+，反之取-。Pi-k用于更式新蜂群位置，β为收缩膨胀因子，其计算公式如(38)—(39)所示。

Pi-k=φ·ppbest_i-k+(1-φ)pglobal_i

(38)

(39)

式中：pglobal_i为当前蜜源i附件蜂群的全局最优位置；φ为取值在(0,1)中的学习系数；Tmax为最大迭代次数；t为当前迭代次数。

9)判断是否有蜜源被舍弃。若蜜源i在经过多次迭代求解后全局最优得不到更新，舍弃该蜜源，引领蜂转变为侦查蜂，重复过程2)。

10)判断是否达到最大迭代次数则输出全局最优蜜源作为优化配置模型最优解，最终根据最优解的各维度数值确定设备安装容量。

4 案例分析

为了证明本文提出的交直流混联微网优化配置模型的有效性，对4种案例进行了分辨率为1 h的全年8 760 h仿真分析，对比弃风率、弃光率、供电可靠性、系统收益等运行参数。案例1：本文提出的计及SOFC余热回收的风-光-氢-冷-储多能互补交直流混联微网；案例2：电网架构为传统交流微网，计及SOFC余热回收，储能系统包含冰蓄冷和氢储能，以交流电网为核心，所有源-荷-储设备都通过双向交直流变换器进行能量耦合；案例3：电网架构为交直流混联微网，储能系统为氢储能和冰蓄冷，不考虑SOFC余热回收；案例4：计及SOFC余热回收，不考虑冰蓄冷和冷负荷需求，储能系统只有氢储能，电网架构为交直流混联微网。

上述4种案例，以案例1为核心，通过控制有无余热回收、系统拓扑结构、储能类型等变量设置，对比案例的差异，从而证明本文所提方法的合理性、有效性。

4.1 模型验证

4.1.1 经济性分析

本文选取ABC-QPSO算法对4种案例进行求解，各案例优化配置方案及收益如表1所示。

表1 各案例优化配置方案及其收益Tab.1 Case-by-case optimal allocation scheme and benefits

从表1可以得到以下结论。

1)案例1拥有最佳的经济性，相比于案例2、3，由于结合了交直流混联和SOFC余热回收，提高了能量利用率，因此在同等负荷需求的情况下，电能更加充足，风光电源和SOFC的安装容量更小。

2)对于一些经济不发达但风光资源丰富的地区，本文提出的方案可以很好地降低投资成本和规划难度。

3)巨大的年供电量可以降低能源产业对化石燃料的依赖性，根据《中国电力行业年度发展报告2020》中火电厂平均供电标准煤耗和单位发电量的二氧化碳排放统计，本文所提系统每年可节约大约11 736 t标准煤，减排21 101 t CO2，对于促进多能互补资源的清洁高效综合利用，推动能源产业的升级，克服我国严峻的能源短缺和环境污染困境具有重要的理论和实践意义。

4.1.2 负荷供给稳定性分析

电、氢、冷负荷的供给缺失率是优化方案的重要考核指标，分别用负荷失电率(loss of power supply probability, LPSP)、负荷失氢率(loss of hydrogen supply probability，LHSP)、负荷失冷率(loss of cold supply probability，LCSP)表示，计算方法如式(40)—式(42)所示。

(40)

(41)

(42)

图2—4分别为全年LPSP、LHSP、LCSP分布图。

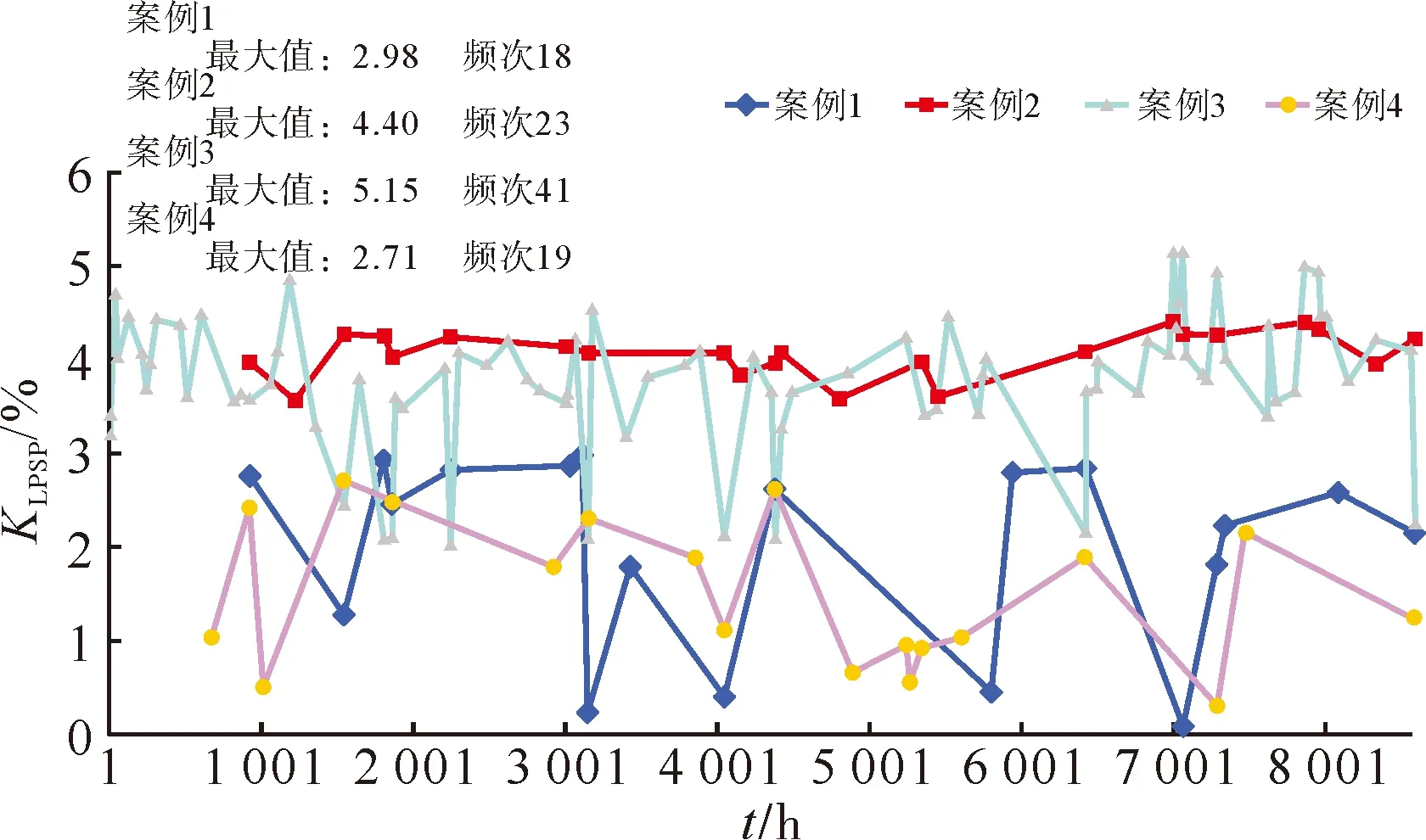
图2 全年LPSPFig.2 Annual LPSP

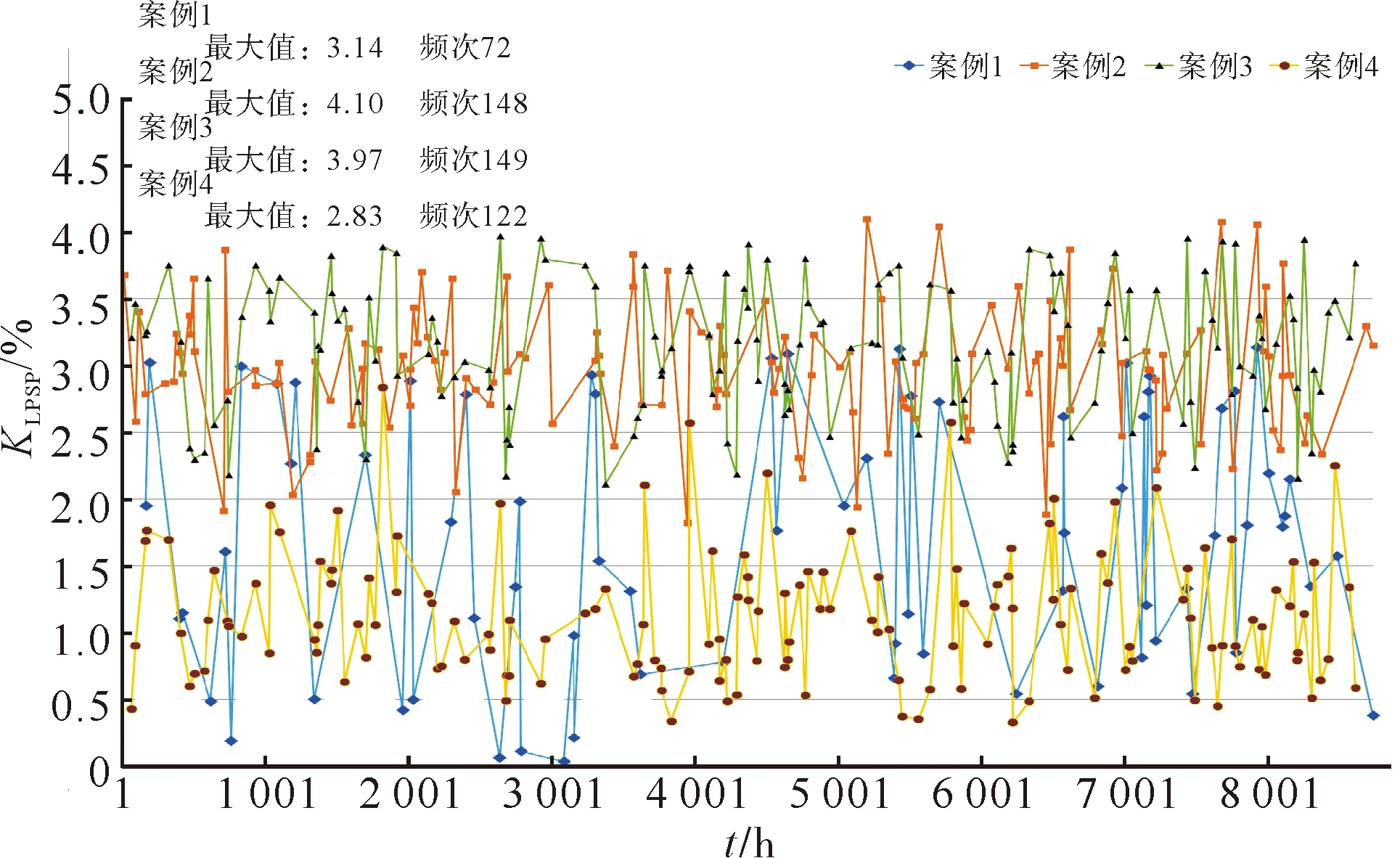
图3 全年LHSPFig.3 Annual LHSP

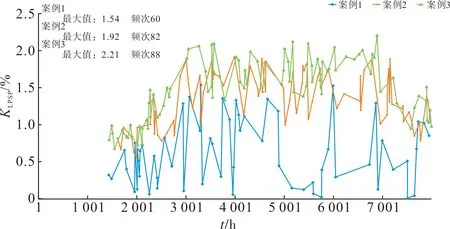
图4 全年LCSPFig.4 Annual LCSP

过高的负荷供给缺失率会使系统安全性下降。图2—4显示了4种案例的全年逐小时LPSP、LHSP和LCSP，由于案例4不考虑冰蓄冷和冷负荷，因此图4只对案例1—3做出分析。

从图2—4可以得到以下结论。

1)本文所提出的优化配置模型能最好地保证电负荷可靠供给，相比于案例2—3，本文的优化模型创新性地结合了交直流混联、SOFC余热回收，在一定程度上提高能量利用率，包括LPSP、LHSP、LCSP，无论是峰值或是频次都得到了极大改善。

2)由于冷负荷具有季节波动性，LCSP集中在7、8月份附近。案例4单独不考虑冰蓄冷，对于用电、氢负荷的供给影响关联性较弱，因此和案例1相比负荷电、氢供给缺失率变化不大。

4.1.3 弃风、弃光率分析

储能设备可以降低弃风、弃光率[25]，案例1和案例4的弃风率、弃光率分别如图5—6所示。

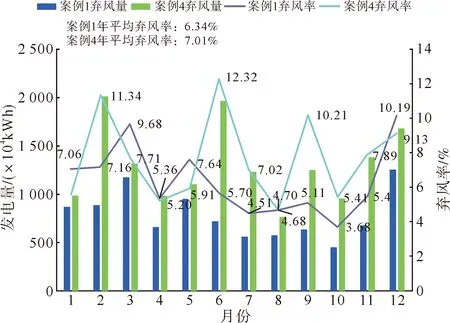
图5 弃风率对比Fig.5 Comparison of wind energy abandoned rates

图6 弃光率对比Fig.6 Comparison of PV energy abandoned rate

通过图5—6可以得到以下结论。

1)相比于单一的氢储能方式，案例1采用氢-冷双重储能机制，提高了风光资源利用率，弃风率、弃光率都比案例4更低，同时可看出季节性波动的冷负荷对风光消纳的影响，冷负荷需求较大的6、7、8月，弃风、弃光率更低，平均弃风、弃光率分别达到了4.96%、2.99%，总共多发电能6.057 06 MWh。

2)在1、2、12月中，由于冷负荷需求为0，弃风、弃光率更高，此时案例1中的冰蓄冷和LBR处于停机状态，因此也间接证明了本文提出的储能方式对提高风光利用率的有效性。

3)较低的“弃风弃光”率可以促进风光资源的高比例消纳，在当下国家对可再生能源大力发展的背景下，本文所提方法能够加快我国风电、光伏、氢能等新能源的发展，加快能源结构全面转型。

4.2 算法对比

为了验证本文所提ABC-QPSO算法的有效性，将该算法与ABC算法和QPSO算法进行了对比，得到的收敛结果如图7所示。

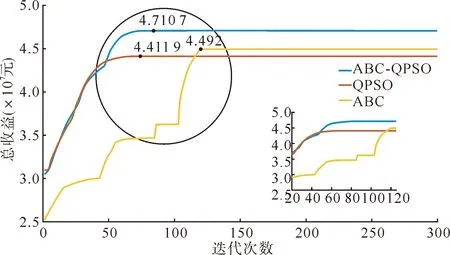
图7 算法收敛特性对比Fig.7 Comparison of convergence characteristics of algorithm

从图7中可以得出以下结论。

1)QPSO算法由于处于量子束缚的随机运动状态，收敛速度最快，但全局搜索能力欠佳，过早陷入局部最优。

2)传统的ABC算法中3种蜂群之间角色可以互相转化和对劣质蜜源的记忆能力，有着更好的全局搜索能力，但在接近全局最优时易陷入局部最优，后期收敛速度较慢，同样存在算法早熟的问题。

3)相比而言，ABC-QPSO算法兼顾了收敛速度和全局搜索能力，证明了本文所提算法的有效性。

5 结论

本文提出的计及SOFC余热回收的氢-冰储能交直流混联微网优化配置模型，应用全年运行数据进行仿真分析，采用ABC-QPSO算法，得出储能容量优化配置结果。分析仿真结果得出以下结论。

1)在风光、负荷数据不变的情况下氢储能-冰蓄冷双重储能机制拥有比氢储能、冰蓄冷更好的经济性，能够最高比例地消纳风光资源；

2)以光伏直流电解水制氢、风力交流电冰蓄冷为核心的交直流混联微网可以减少电能变换造成的能量损失，从而提高负荷供给可靠性和经济性；

3)SOFC-MGT-LBR的余热回收结构可以将能量梯级利用进行电-冷联产，实现氢能源高效利用，进一步提高了系统的经济性、可靠性。