大容量锂电池储能电站的等值仿真方法

周姝灿，卢洵，刘新苗，龚贤夫，左郑敏，彭虹桥

(1. 广东电网有限责任公司电网规划研究中心，广州510620；2. 广东电网有限责任公司，广州510620)

0 引言

锂电池储能电站由于其资源配置灵活、响应速度快、不受天气以及地理位置的影响等优势，在促进可再生资源整合和提高系统运行灵活性中体现了巨大的潜力[1 - 3]。其中，在不可调度的间歇发电资源渗透率较高的系统中，大规模电网侧储能电站可以有效地抑制频率波动、电压波动，具有削峰填谷的作用，受到了国内外储能领域的重点关注[4 - 6]。例如，2018年江苏镇江东部为缓解燃煤机组退役对用电高峰的影响，投运了总功率为101 MW、总容量为202 MWh的8座储能电站，是目前世界最大规模的储能项目，可实现万千瓦等级在毫秒级的负荷响应，在用电高峰期发挥了极强的顶峰作用，大幅提高了江苏电网对可再生能源的接纳能力[7]。2021年4月21日，国家发改委、国家能源局在《关于加快推动新型储能发展的指导意见(征求意见稿)》中指出，到2025年，新型储能总装机规模达30 GW以上，其中在电网侧关键节点布置大容量锂电池储能将成为实现电力系统碳达峰碳中和的关键支撑之一。

目前国内外对大容量储能电站的建模与仿真方法的研究多针对储能电站的某一组成部分，而少有文献对储能电站的整体建模与仿真进行总体介绍和研究。文献[8]中建立了储能电站中电池的戴维南模型并采用扩展卡尔曼滤波方法进行荷电状态估计，以模拟电池的动态特性，文献[9]在单体锂电池模型的基础上进行缩放以等效建立储能电站的电池组模型。文献[10 - 11]中建立了储能电站的协同控制模型，解决了多储能单元之间的电压和频率异步问题。文献[12 - 13]虽然提出了储能电站的整体建模与仿真方法，但缺乏对建模与仿真细节的阐述，不便于进一步探究。

本文从锂电池组建模、储能变流器和换流变参数设计、控制策略以及等值建模方法4个方面详细阐述了锂电池储能电站仿真建模中的关键方法，并基于江苏镇江东部电网侧百兆瓦级锂电池储能电站的布置方式和设计参数在PSCAD 4.6.2中搭建了大容量锂电池储能电站的等值仿真模型。最后，仿真测试验证了所提出的等值仿真方法的正确性。

1 大容量储能电站布置方式

如图1所示，目前大容量锂电池储能电站一般采用户外集装箱式电池舱布置方案。电池舱作为一个储能单元，主要由锂电池组、储能变流器(power conversion system PCS)、换流变压器、电池管理系统(battery management system，BMS)等组成。电池舱内锂电池组由单体锂电池根据电池组额定电压和额定容量进行一定数量的串并联组成，然后通过成套的PCS以及换流变压器升压至指定电压。整个储能电站根据总容量由多个电池舱并联组成，各电池舱的运行状态由其内部的BMS监测，其相关运行状态数据上传至总站的数据采集(supervisory control and data acquisition，SCADA)和能量管理系统(energy management system，EMS)，上级电网调度中心可通过实时以太网和百兆以太网与总站的SCADA和EMS通信，以监控储能电站整体运行状态并控制PCS运行[14]。

图1 大容量储能电站布置方式Fig.1 Layout mode of large capacity energy storage power station

2 大容量锂电池储能电站建模

2.1 锂电池组建模

锂电池组由单体锂电池串并联组成，因此电池组建模主要包括单体锂电池模型和串并联模型两部分。常用的单体锂电池的等效电路模型包括Linear模型、Thevenin模型、PNGV模型和MC模型[15]。其中MC模型能充分反应电池的动态电气特性，建模精度较其他3种等效模型更高，但MC模型随着并联RC网络的增加参数辨识将变得十分困难，在当前锂电池建模的研究中，通常采用二阶RC网络，作为建模精确度与复杂度之间的最佳折衷。二阶MC模型的等效电路图如图2所示。其中，Ibatt为充放电电流；Uoc为开路电压；R0为电池内阻。两个RC网络中的极化电阻Ri和极化电容Ci刻画锂电池的极化电压特性，其中一个RC网络中的R1和C1描述电池的短期暂态过程，另一个RC网络中的R2和C2描述电池的长期暂态过程。电路中的所有非线性电路参数都是荷电状态(state of charge，SOC)的函数，曲线拟合方法常用于获取非线性电路参数的具体表达式，表达式的一般形式如式(1)所示。通过安时积分等方法估算出的SOC值可用于实时更新各电路参数，以实现锂电池的精确建模。

(1)

式中：KSOC为电池荷电状态；Uoc为电池开路电压函数，λoc、aoc、boc、coc、doc、foc为Uoc表达式的各项拟合参数；R0为电池内阻函数，a0、λ0、f0为R0表达式的各项拟合参数；Ri为第i个电池极化电阻函数，aRi、λRi、fRi为Ri表达式的各项拟合参数；Ci为第i个电池极化电容函数，aCi、λCi、fCi为Ci表达式的各项拟合参数，i∈1, 2； 以上拟合参数均为常数，由实际电池测试数据拟合确定。

图2 二阶MC锂电池模型Fig.2 Second-order MC lithium battery model

锂电池组建模中对单体电池进行串并联有两种方式：先串后并和先并后串。根据工程建设经验，采用先串后并(Ns个单体电池串联组成一个电池堆，然后Np个电池堆并联)的电池组布置方式有利于后期电池检测与更换[16 - 17]。假设储能电站采用规格参数完全相同的单体锂电池，忽略串并联支路的能量利用率和电流不平衡度对电池组整体性能的影响，电池组的串并联数的确定如式(2)—(3)所示。

(2)

(3)

式中：Ns、Np分别为电池组中单体电池的串联数和电池堆的并联数；Upack为电池组的额定输出电压，kV；Ubattery为单体电池的电压，V；Spack为电池组的额定容量，MWh；Cbattery为单体电池的额定容量，Ah。

2.2 PCS和换流变参数设计

PCS的换流电抗器作为PCS与电网进行能量交换的中间环节，对实现两者之间的功率交换、滤波以及故障恢复发挥着至关重要的作用。换流电抗器包括换流变压器漏抗和相电抗器，在设计时应根据PCS无功功率输出范围以及输出电压增益确定，此外还要满足电流跟踪速度的要求和电流谐波的要求[18 - 19]。具体而言，换流电抗器的电感L应满足式(4)。

(4)

换流变压器可以降低PCS允许损耗和电压电流谐波分量以及隔离交直流零序分量，其二次侧额定电压值直接影响PCS有功无功功率的运行范围，在选择二次侧电压时应考虑直流电压、直流电压利用率、调制比、换流电抗器以及PCS运行范围。

2.3 储能电站控制策略

储能电站的控制策略体现在对PCS的控制上，通过一系列控制策略使得PCS能够控制储能单元的充放电功率、维持交流侧电压，减小并网波动。如图3所示，储能电站的上层控制包括定PQ控制、定交流电压控制、内环电流控制、孤岛模式下的V/f控制以及调制波的生成模块[20 - 21]。

在并网模式下，PQ控制采用内外环解耦的控制方式。外环控制中，有功功率类控制采用定有功功率控制，以控制储能电站以设定功率进行充放电；无功功率类控制采用定无功功率控制或定交流电压控制，以控制储能电站的无功功率或维持交流母线电压。如图3所示，正常情况下采用定无功功率控制，即故障信号开关打开，系统此时没有故障；当系统出现故障时，故障信号开关关闭，此时采用定交流电压控制。在孤岛模式下采用V/f控制，维持交流母线电压和频率保持不变。此外，外环控制中还包括Q/V、P/f下垂控制以实现有差调节；电流限制模块用于限制暂态下的故障电流。内环电流控制通过外环控制传递来的d轴和q轴电流信号进行PI调节以生成的d轴和q轴的电压分量，经极坐标变换后得到理想调制波的幅值和相角，再由dq-abc变换单元，产生调制波所需的abc三相电压，传递至下层控制单元，实现PCS阀级开关动作。

根据电化学储能系统PCS技术规范GB/T 34120—2017[22]，当PCS交流侧电压d轴分量降低至0.85以下或超过1.2出现低压穿越或高压穿越时应保证储能变流器不脱网连续运行；否则，允许储能变流器切出。对故障期间没有切出的储能变流器，其有功功率在故障解除后应能快速恢复，从故障解除开始，以至少每秒30%额定功率的变化率恢复至故障之前的值。在交流侧由于短路故障等发生电压跌落时，PCS注入电网的动态无功电流IT应实时跟踪并网点电压变化，并应满足式(5)。

(5)

式中：UT为PCC点电压标幺值：IN为PCS额定电流标幺值。

2.4 储能电站等值建模方法

大容量储能电站一般采用多个PCS并联的布置方式，即由多个小容量储能单元(如0.5 MW/1 MWh)并联组成。在对储能电站进行建模与仿真时，若对组成储能电站的全部小容量储能单元均进行单独建模将会大大降低模型的计算速度与效率。由于各储能单元输出外特性基本一致，故在进行建模时可以对储能电站进行等值，将单个储能单元容量等值放大以建立所需容量的储能模型。本文参考PSCAD Type4风电场模型建立缩放单元模型。将小容量储能单元的输出电流扩大一定倍数，然后通过可控电流源注入交流系统，扩大注入交流系统的功率，从而等效建模百兆瓦级储能电站的功率输出。此缩放元件会产生少量无功功率，所以采用电流源进行缩放建模，适用于对少量无功功率的增加没有影响的系统。缩放单元的模型如图4所示，缩放单元的建模类似于n-1条并联的无损传输线，传输线阻抗X参考PSCAD中Type- 4 Wind Turbine 模型取为0.025 p.u.，n为需等值的储能电站总功率与单个储能单元输出功率的比值，缩放单元中的总注入电流为(n-1)iabc，总阻抗为X/(n-1)，其中，iabc为储能单元输出的三相电流瞬时值。

图4 缩放单元模型Fig.4 Scale unit model

3 大容量锂电池储能电站仿真

根据第2节提出的大容量储能电站建模方法并参照江苏镇江东部电网侧百兆瓦级储能电站的布置方式和系统参数，如电池组容量为1 MW/2 MWh，以及PCS升压舱内PCS的额定容量等。本文在PSCAD中搭建了大容量锂电池储能电站的等值仿真模型，如图5所示。

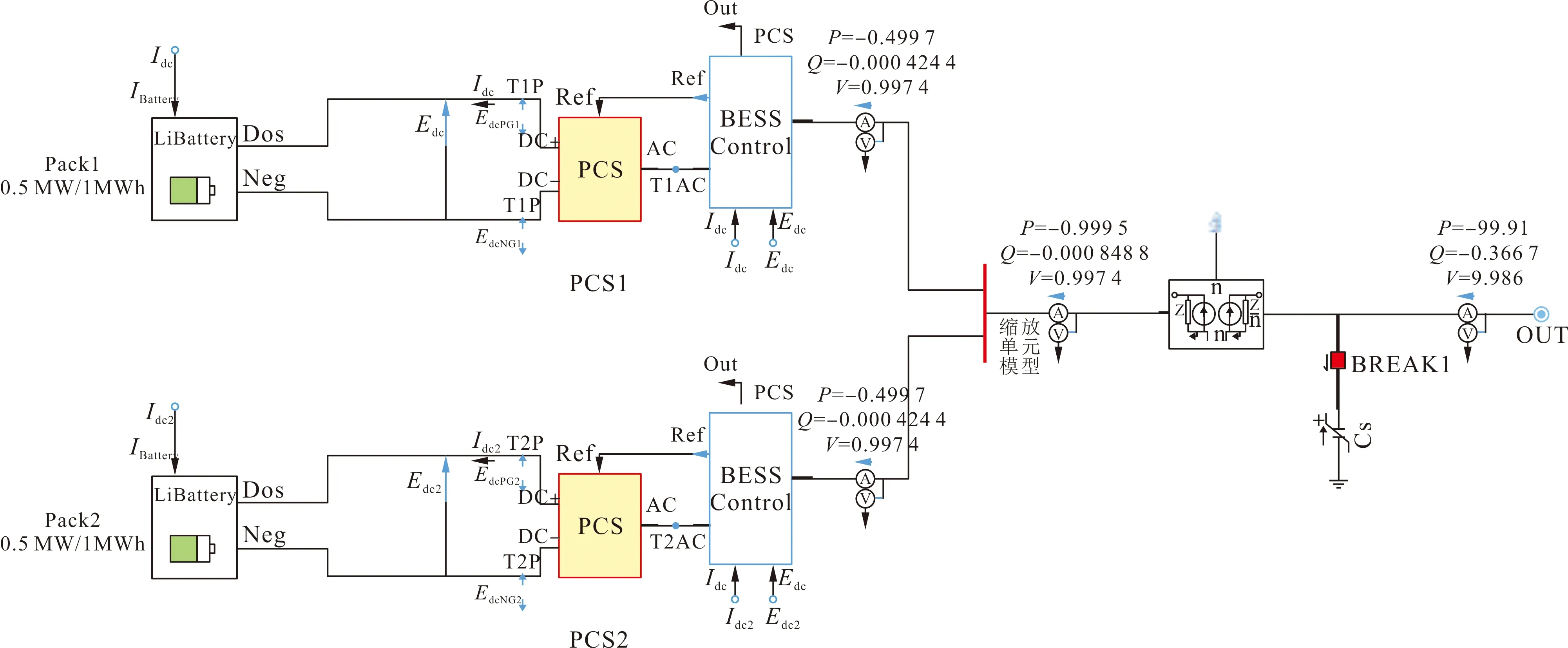
图5 基于PSCAD的储能电站仿真模型Fig.5 Simulation model of energy storage power station based on PSCAD

该模型采用两个0.5 MW/1 MWh的储能单元并联、每个储能单元配置一个500 kW的PCS和一个550 kVA换流变压器升压至10 kV[23]。为了模拟百兆瓦级的储能功率输出，根据2.4节储能电站等值建模方法，经并联形成的1 MW/2 MWh储能单元模型通过功率缩放单元将输出功率扩大100倍，以等值建模百兆瓦级的储能电站，最后通过升压变压器接入220 kV电网。模型具体参数如表1所示。

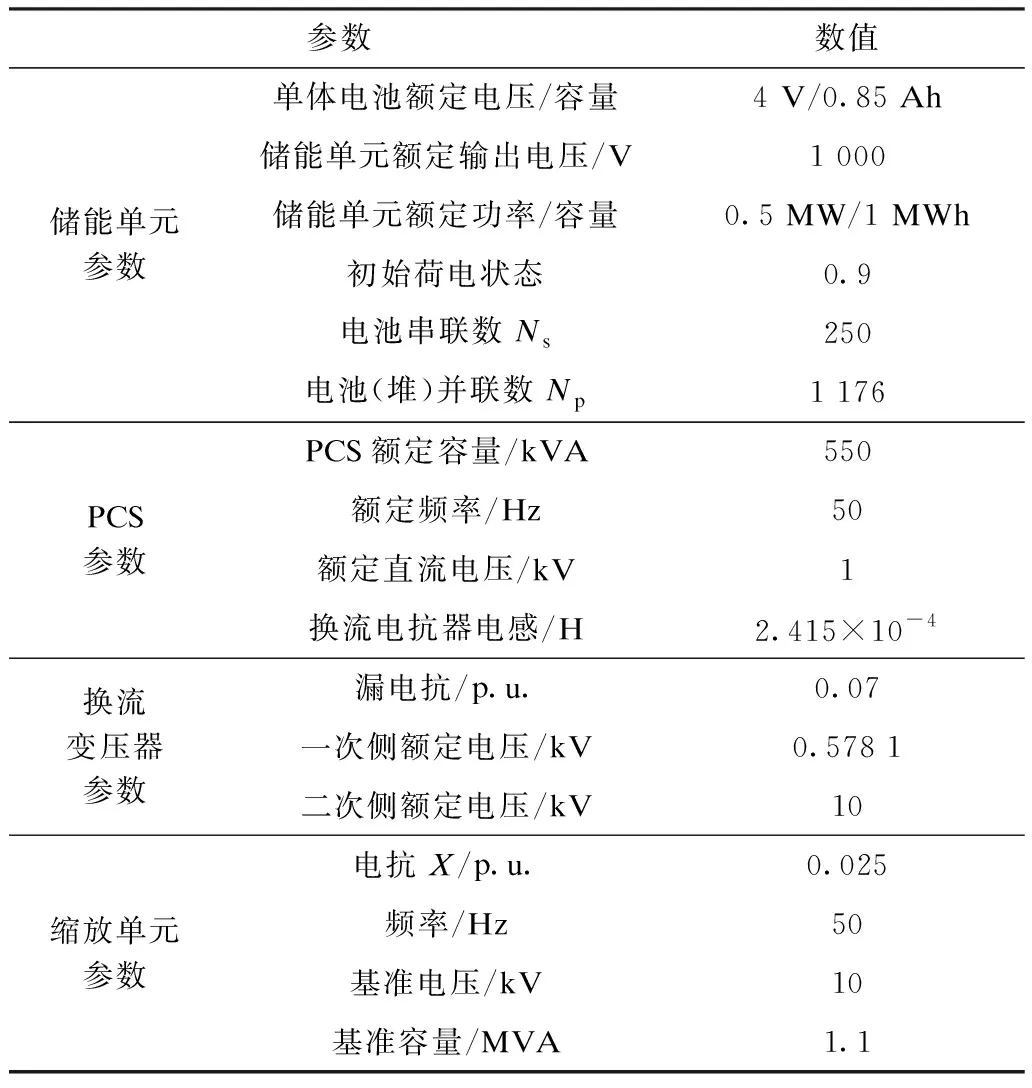
表1 储能电站仿真模型参数Tab.1 Simulation model parameters of energy storage power station

3.1 储能单元仿真测试

本文单体锂电池采用中国TCL超级电池公司的商用锂离子聚合物电池产品TCL-PL- 383562(电池规格为4 V/0.85 Ah)的实验拟合参数，具体参数表达式详见文献[16]。采用第2.1节所述电池组建模方法在PSCAD中搭建的电池组仿真模型如图6所示。为搭建额定输出电压为1 000 V的0.5 MW/1 MWh储能单元模型，由式(2)—(3)求得Ns应取250，Np应取1 176。SOC值可通过安时积分法获得。

图6 电池组仿真模型Fig.6 Battery pack simulation model

3.1.1 单体锂电池Voc测试

单体锂电池的建模准确性是储能单元及储能电站模型准确性的基础。锂电池二阶MC模型中的非线性电路参数由实验曲线拟合获得，准确性可得到保障。其中，开路电压Voc(KSOC)作为可控电压源的电压输入代表了锂电池的能量源，是锂电池参数中最为重要的部分。文献[16]在80 mA的恒定放电电流下放电约37 000 s测试了单体锂电池Voc的变化曲线。本文将放电电流扩大1 000倍，即在80 A的放电电流下仿真37 s，以等效该实验场景，仿真曲线与实验曲线(将实验所得曲线的时间坐标相应减少1 000倍)的对比如图7所示。

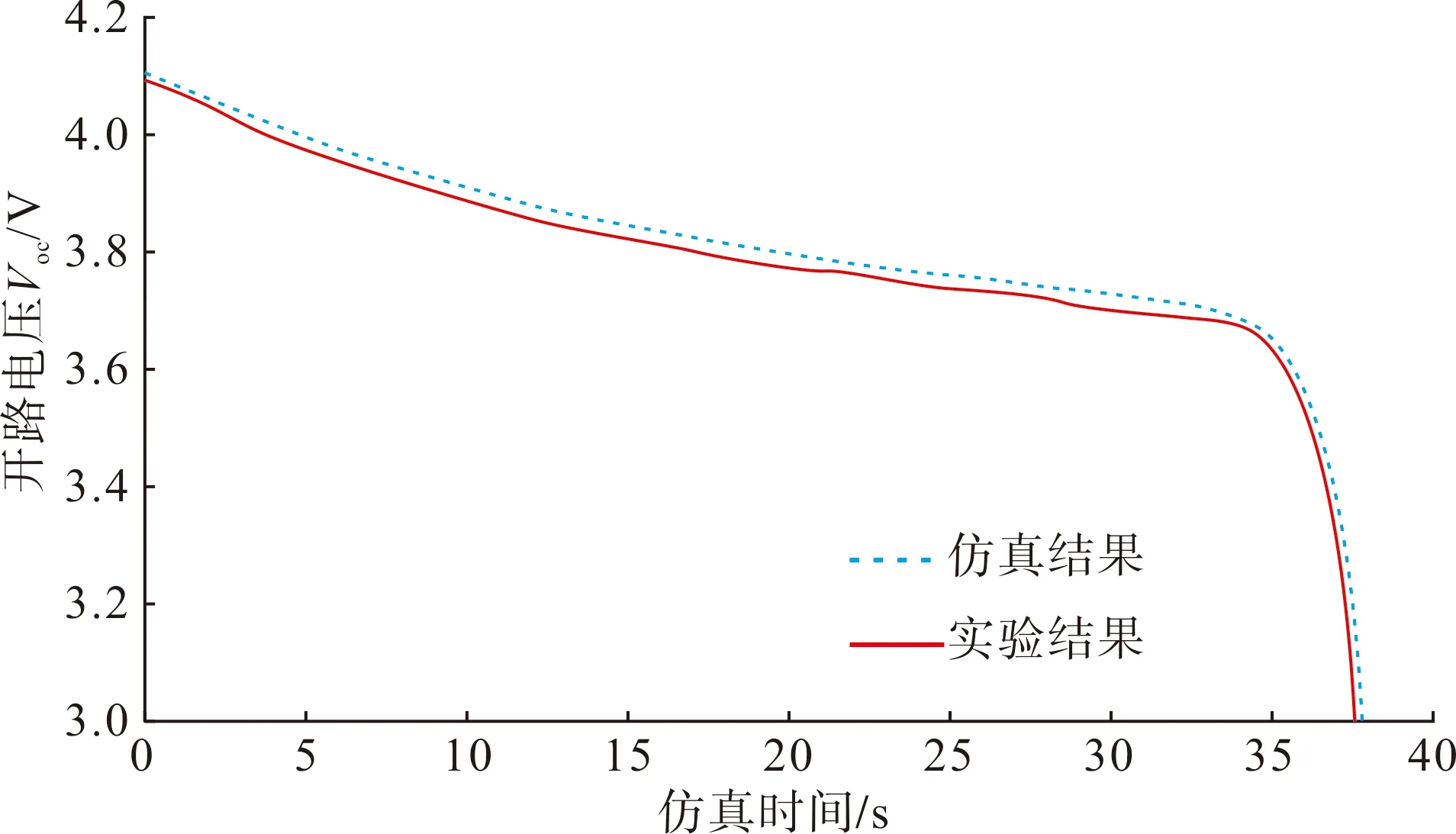
图7 单体锂电池Voc测试曲线Fig.7 curves of Voc test of single lithium battery

PSCAD仿真结果与参考文献中的实验结果基本一致，验证了本文搭建的锂电池模型的正确性。限于文章篇幅，对于参考文献中不同放电电流下的Voc变化不再一一对比。

3.1.2 充放电测试

根据文献[24]，在热备用状态下，对0.5 MW/1 MWh储能单元进行如下充放电测试：分别将储能单元有功功率设定值Pref设置为-0.25PN、 0.25PN、 -0.5PN、 0.5PN、 -0.75PN、 0.75PN、 -PN和PN(PN为额定充放电功率，取PN=0.5 MW， 功率设定值为负值表示放电，为正值表示充电)，每个设定值运行3 s，并分别进行±1.1PN的过载测试，所得测试曲线如图8所示。

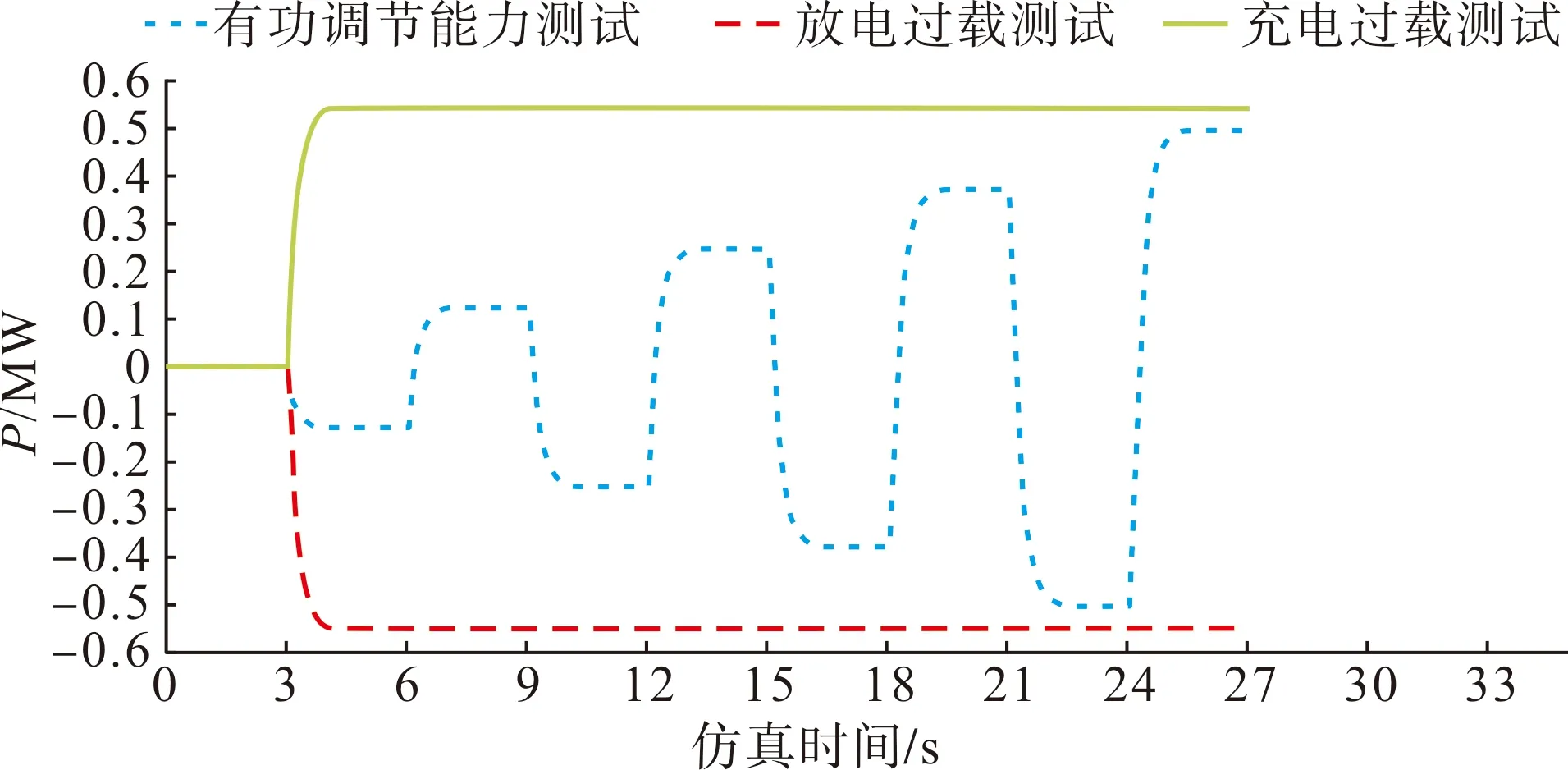
图8 充放电测试曲线Fig.8 Charge-discharge test curves

由图8可得，储能单元的充放电功率可准确跟踪功率设定点且具备±1.1PN的过载充放电能力，平均功率控制精度为0.508 8%。具体的充放电响应时间、充放电调节时间、充放电转换时间测试结果如表2所示，测试结果均满足国标GB/36547—2018[25]的要求。在以上功率设定值时储能单元的SOC曲线如图9所示，随着充放电功率的增加，SOC值的变化率增加，但由于储能单元的容量为1 MWh而仿真时间以秒为单位，SOC值从初始的90%开始到仿真结束时只会发生微弱变化。

表2 充放电响应时间、调节时间和转换时间测试结果Tab.2 Simulation model parameters of energy storage power station

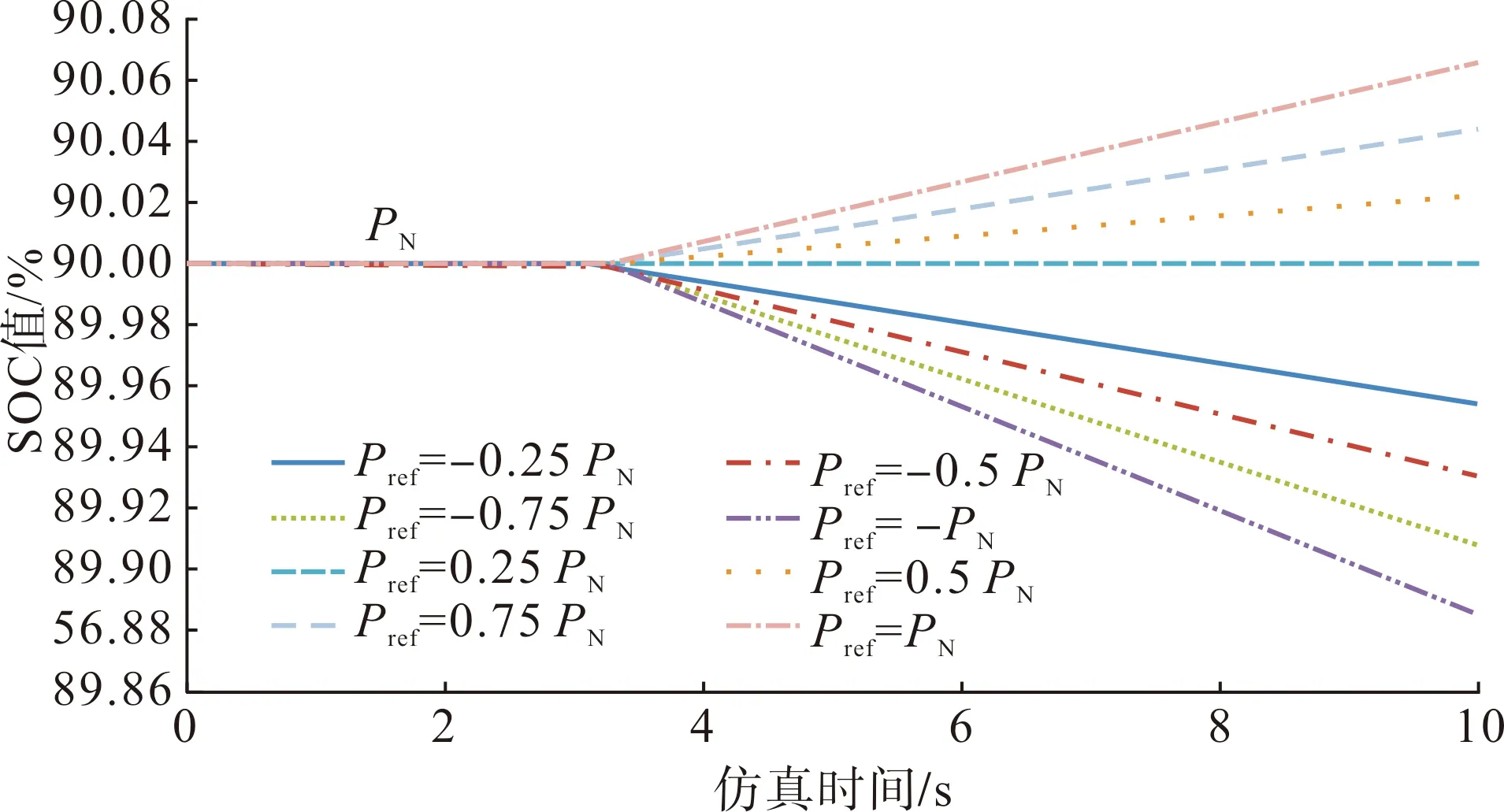
图9 SOC测试曲线Fig.9 State of charge test curves

3.2 储能电站仿真测试

3.2.1 充放电测试

在两个并联储能单元的基础上通过设置缩放单元的缩放因子分别为1、30、80、100时进行充放电测试，测试所得曲线如图10所示。

图10 不同缩放因子下的充放电功率测试曲线Fig.10 Charging and discharging power test curves under different scaling factors

储能电站模型的充放电功率可准确跟踪到设定值，平均控制精度为0.508 8%，与不经缩放的储能单元模型的控制精度相同。此外，对额定功率为100 MW的储能电站模型进行与3.1.2节相同的充放电测试，测试结果如图11所示，储能电站模型的充放电功率可准确跟踪功率设定点且具备一定过载充放电能力，充放电响应时间、调节时间、转换时间与表2基本一致，故测试可得缩放单元可实现对储能电站充放电特性的等值建模且基本不会影响功率控制效果，由于每次测量结果都会有偏差，存在一定的精度，所以百兆瓦级储能电站模拟的平静精度为多次测量结果的平均值。

图11 充放电测试曲线Fig.11 Charge-discharge test curve

3.2.2 故障测试

6 s时在PCC点设置三相金属性短路故障，故障持续0.12 s，测试所得储能电站输出功率、外环电流分量以及PCC点线电压有效值如图12所示。

图12 三相短路故障测试曲线Fig.12 Test curves of three-phase short circuit fault

当故障发生时，储能电站模型输出的有功功率从100 MW骤降至20 MW，输出无功功率从0突增至30 Mvar以支撑交流侧电压；PCC点线电压有效值降低至0.85 p.u.以下，此时低电压穿越模块发挥作用，为维持交流侧电压，定无功功率控制切换为参考值为1 p.u.的定交流电压控制，外环电流分量不超过低电压穿越限值(如图12(c)所示)。随后在故障清除后可以看出功率、电压、电流迅速恢复到初始值，暂态过程持续时间较短。

4 结语

本文从锂电池、储能变流器及换流变压器参数设计、控制策略以及等值方法4个部分详细阐述了大容量储能电站的仿真建模方法，根据所提出的建模方法参照江苏镇江东部电网侧百兆瓦储能电站的系统实际设计参数，在PSCAD中搭建了大容量储能电站的电磁暂态仿真模型。按照储能系统接入电网的相关测试规范，对所搭建的储能电站仿真模型进行充放电特性测试和故障测试，测试结果表明，所建模型具备大容量储能电站接入电网侧的外特性分析仿真能力。在未来的研究中，将利用本文所搭建的等值仿真模型进行大容量储能电站在电网侧的电压、频率响应研究和削峰填谷能力分析。