考虑配电网可靠性的储能系统选址定容优化
王凯亮,孔慧超,李俊辉,吴新雄,李海波,江坷滕,郝中汉
(1.广东电网有限责任公司东莞供电局,广东 东莞523008; 2. 清华四川能源互联网研究院,成都610000)
0 引言
配电网位于电网末端,接近电能传输终点,元件多、结构复杂,直接影响用户的供电状况[1 - 3]。我国通过制订配电网建设标准、加大电网建设投资、优化可靠性算法模型、开发可靠性分析软件等技术手段,使得我国配电网的可靠性水平逐步走到世界前列[4 - 6]。当前世界发达城市的年均停电时间不足1 h。其中,新加坡可靠性水平居世界领先地位,在2011年便已经达到用户年均停电时间低于1 min;慕尼黑用户年平均停电时间约15 min,2017年纽约市用户年均停电时间在1 h之内[7 - 9]。我国在2015—2019年间城市地区年均停电时间在4.08~5.20 h/户之间,与发达国家和地区的可靠性水平还有较大差距,而部分城市如珠海、中山、厦门等城市年平均停电在1 h之内,达到了世界领先水平,因此我国可靠性水平差异大,还有很大提升潜力[10]。
在“双碳”背景下,新能源在发电系统中占比逐渐上升,因此也催生出大批分布式储能装置的需求[11 - 13]。随着储能经济技术的快速发展,近年来,以电化学储能为代表的储能技术已经在电源侧、用户侧和电网侧获得了广泛应用。储能可有效改善分布式电源的间歇性波动特性,同时与转供电系统相互配合作用,有助于提高系统运行可靠性[14]。然而,各类储能技术有着不同的特点和适用场景,将其应用于电网中还需要较完善的运行规划技术、技术经济分析和应用场景研究[15]。因此本文旨在考虑系统经济性的前提下,以提高配网可靠性为目标,优化储能的布点和容量规划。
当前业内的研究人员提出了多种提高可靠性的手段,例如,文献[16]提出带电作业技术可以降低计划停电的频率和时间从而提高可靠性,然而,由于目前带电作业的安全性尚需提高且推广难度较大,配电网带电运行的全覆盖仍存在很大挑战;文献[17 - 18]建立了不同自动化开关设备的可靠性模型,同时研究了在系统中安装自动重合闸、断路器、分段开关等自动化设备时系统可靠性的变化。应用这些配电自动化设备可以快速精准定位故障所在并将其隔离,便于迅速展开抢修。然而,由于从故障定位方面仅能减少故障识别时间,无法减少故障修复时间,因此该方法对系统的可靠性提升效果有限。文献[19 - 20]提出将配电自动化技术应用于转供电系统能够极大地减少复电时间,但是没有针对转供电对可靠性的影响进行量化分析。其他改进可靠性的方式,如改用柔直设备等的研究并未完全成熟,全面推广还需更多的研究成果[21 - 22]。
对于当前储能系统选址定容问题多是针对削弱分布式能源出力波动性和提升系统峰谷套利的经济性开展研究,北方工业大学的李建林等人研究了多目标粒子群算法的选址和容量配置方案[23],并对该算法做出了改进,可应用于不同场景且经济适用性好,但并没有考虑对系统可靠性的影响。文献[24]考虑了极端事件下配电网的韧性,提出了基于场景生成与缩减算法的优化方案,对实际工程中储能系统的规划有很大的参考价值。但由于不同场景配电系统可靠性分析相关性低、复杂度大,难以将其中的算例推广到一般的配电系统。孟源等人提出的储能系统选址定容考虑了N-1安全约束[25],对配电系统的优化具有指导意义,但目标函数面向对象是风光联合储能系统,缺乏对系统可靠性影响的分析。
在储能应用于系统可靠性提升方面,清华大学的程林等学者综述了储能接入配电系统的可靠性研究,为评估含有分布式能源配电系统的可靠性提供了指导方法[14]。加拿大萨省大学的 P. Gautam 选用蒙特卡罗模拟计算含有储能的配电系统可靠性,该模型对实际含有储能的配电系统适用性强,但并未涉及储能的选址定容问题[26]。文献[27]对伪时序状态转移采样法进行了改进,大大提高了计算效率,但其优化模型仅包含储能容量这一单一变量,并未考虑将其与选址结合的多变量联合优化问题。
综上所述,目前对考虑系统可靠性的储能选址定容优化研究较少,储能的合理规划对提高系统可靠性有着重要的意义,因此亟需开展相应研究。本文首先考虑储能的充放电特性,依据解析法建立了储能等元件和系统的可靠性模型,其次以系统可靠性和经济性等综合性能最优为目标,结合储能容量限制等约束,建立储能系统的选址定容模型,然后使用遗传算法进行优化求解,最后,以某工程的实际数据为算例,验证了本模型的选址定容结果对于提供系统可靠性的有效性。
1 可靠性模型及可靠性评估方法
1.1 元件可靠性模型
1.1.1 传统可修复元件的双状态模型
传统部件(如变压器、线路、开关)一般分为可修复和不可修复两类。不可修复部件是指投运后出现故障时,维修难度极大或维修费用极高,但是电力系统中绝大多数元件是可修复的。
可修部件的双状态模型包括正常运行和故障修复两种状态。可修部件的状态转换图如图1所示,图中N代表元件正处于正常工作状态,R代表元件处于故障修复状态。参数λ为元件的故障率,参数μ为元件的修复率。

图1 元件的双状态模型Fig.1 Dual-state model of components
1.1.2 储能系统可靠性模型
目前电池储能系统的储能模块多选用磷酸铁锂电池来供能,其组成部分包括能量转换系统(power conversion system, PCS)的电池模组、DC-DC变换器、DC-AC逆变器和滤波器等,在进行配电系统可靠性分析时,可以将这些元器件等效为一个串联系统。同时,假设故障各部分相互独立,采用状态空间分析方法建立状态转移模型,状态转移图如图2所示,图中状态“0”表示正常运行,状态1—4分别对应各设备故障;λ1~λ4和μ1~μ4分别对应各部分的故障率和修复率。
能量转换系统失效意味着4个主要设备同时失效,串联系统失效状态下的等效失效率λeq和修复率μeq为:
(1)
(2)
以上等效模型可推广至N个元件串联的系统,仅将上式中元件个数替换为N即可[28]。
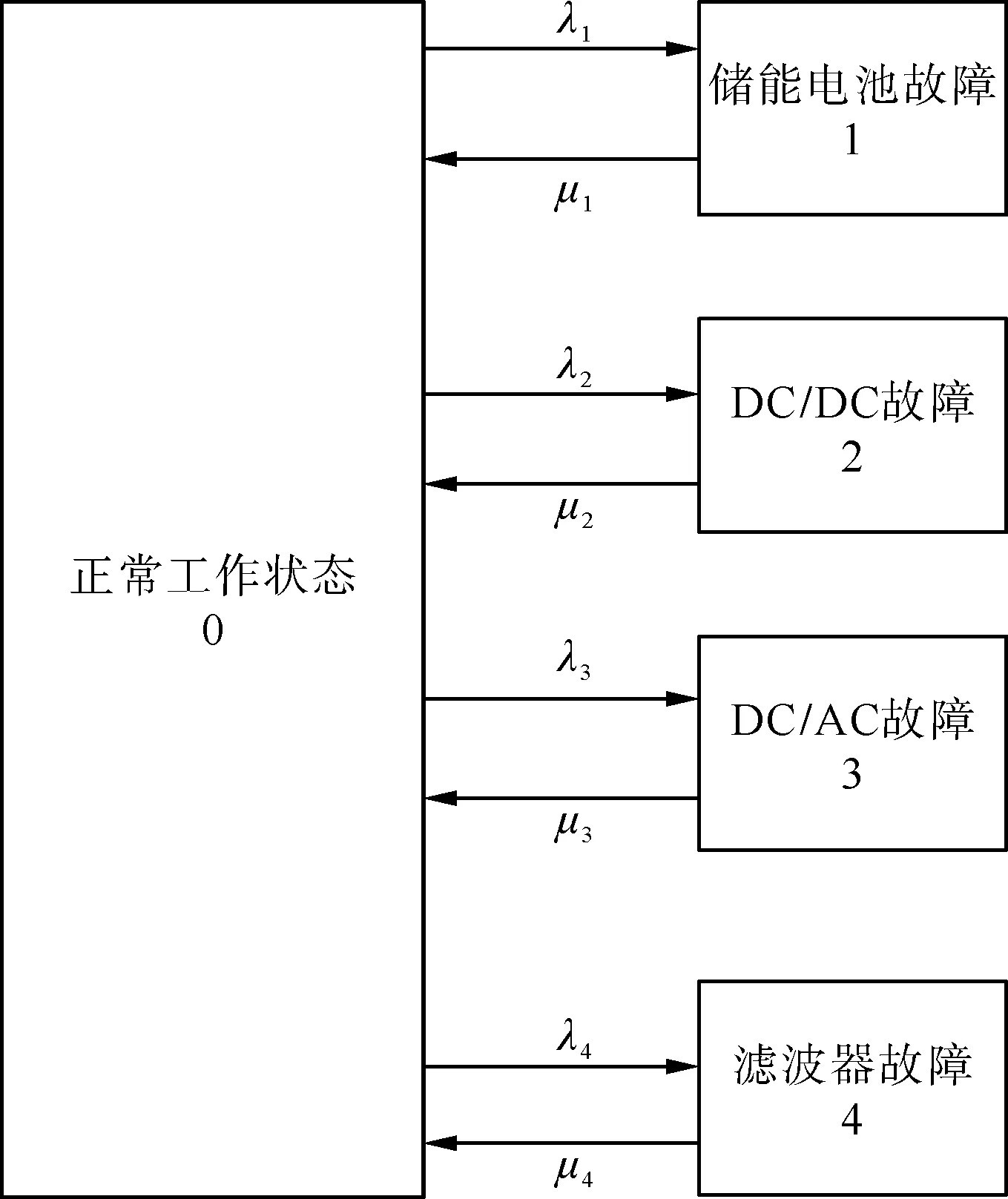
图2 储能系统状态转移图Fig.2 State transition diagram of ESS
1.2 可靠性评估算法
第n个负荷点相对主电源的故障率λfail(n)(次/百台·a)为:
λfail(n)=L(n)λL+nS(n)λS+λT
(3)
式中:L(n)为线缆长度,m;λL为该负荷点线缆故障率,次/百米·a;结合工程实际数据,系统中断路器和开关的故障率接近,那么可以对断路器和开关的故障进行统一分析,nS(n)为负荷点n与主供电电源之间的断路器和开关的数量和;λS为该负荷点断路器和开关的故障率,次/百台·a;λT为该负荷点配电变压器失效率,次/百台·a。
第n个负荷点相对主供电电源的修复时长trepair(n)(h/次)为:
(4)
式中:tL、tS、tT分别为线缆、开关、变压器复电时间,h/次。
当配电系统有转供电线路接入时,第n个负荷点相对主供电电源停运时间tstop(n)(h/次)为:
tstop(n)=(1-rtrans)λfail(n)trepair(n)+rtransλfail(n)ttrans
(5)
式中:rtrans为转供成功率;ttrans为转供时间,h/次。
(6)
式中Nload为系统中所有负荷点的总数量。
(7)
系统可靠性R0为:
(8)
2 储能规划布点技术
2.1 决策变量及约束条件
1)选址约束
针对储能系统的选址定容问题,分别选取第i个负荷点是否接入储能和该接入点储能的容量作为决策变量。因此,储能系统的选址属于0-1整数规划问题。接入点变量x(i)满足如下条件:

(9)
cminNload≤∑x(i)≤cmaxNload
(10)
式中cmin、cmax分别为配电网中允许储能接入负荷点的最小和最大占比。
2)容量约束
储能可放电量EB(i)则可取连续正整数。其约束条件的数学表达式为:
(11)
式中:N+表示正整数集;EB(i)max为储能系统在实际工程中可释放的最大电量。因此,有:
EB(i)max=cBE(i)
(12)
式中cB为储能电池的放电深度,即储能系统允许放电量占总容量的百分比。
2.2 目标函数
以可靠性和经济成本综合指标W最高作为目标函数,即:
maxW=ωECOAECO(C)+ωRAR(R0)
(13)
式中:ωECO、ωR分别为经济性与可靠性所占权重;AECO(C)、AR(R0)为总经济成本和可靠性隶属度函数,其自变量C为总经济成本,自变量R0为系统可靠性,可采用1.2节式(8)中的计算方法求得。
根据实际工程经验,优化的最终目标为经济成本和系统可靠性均达到较高水平。但因为经济成本和系统可靠性的单位不同、量级差异大、与目标相关趋势不同(经济成本越低越好,系统可靠性越高越好),因此分别采用如图3、图4所示的偏小型梯形函数和偏大型梯形函数,对系统经济成本和可靠性进行归一化处理。两种隶属度函数的数学表达式如下:
(14)
(15)
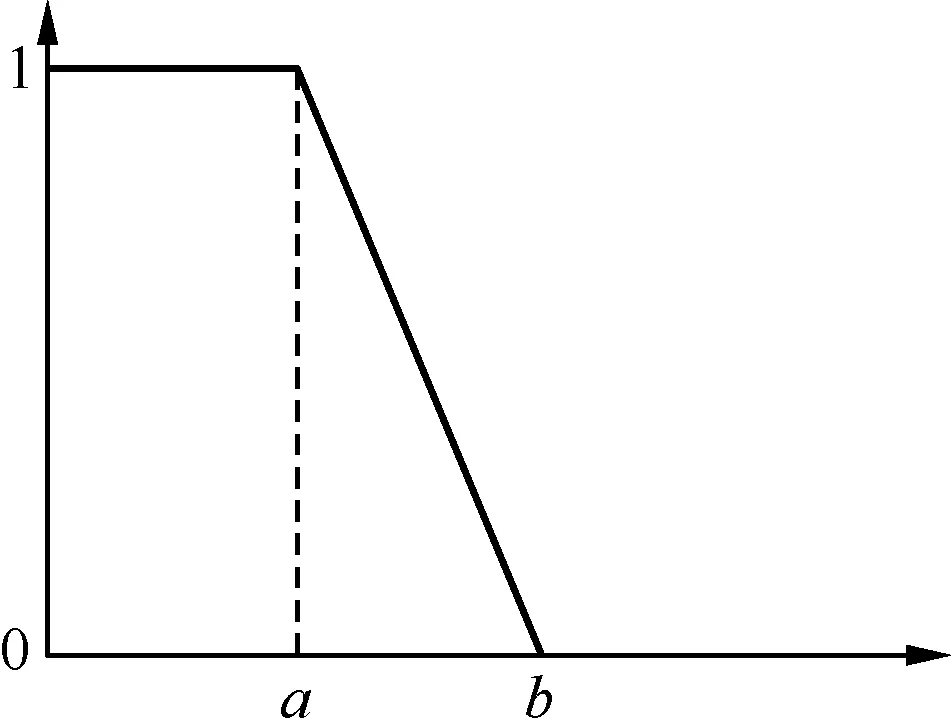
图3 偏小型梯形隶属度函数Fig.3 Descending trapezoidal membership function
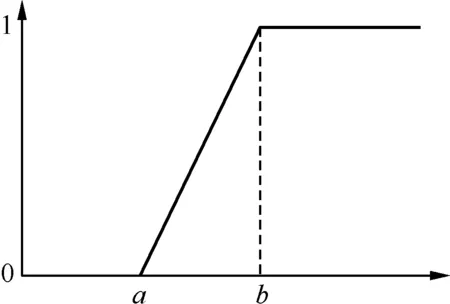
图4 偏大型梯形隶属度函数Fig.4 Ascending trapezoidal membership function
总经济成本C的计算方法如下[29]:
C=CESS+CENS
(16)
式中:C为可靠性评估总成本,万元;CESS为储能电站总成本,万元;CENS为总电量不足成本,元。储能电站总成本CESS可表示为:
(17)
式中:i为有储能系统接入的负荷点;CE为储能电站单位容量的总成本[30],万元/MWh;E(i)为储能系统在第i个负荷点的容量,MWh。
总电量不足成本CENS为:
(18)
式中:EENS(i)为第i个负荷点由于断电造成的缺失供电量,MWh;Ft为缺供电量的罚金值[31],万元/MWh。
总缺失供电量EENS(i)可通过式(19)求得:
EENS(i)=Pitlp(i)
(19)
式中:Pi为第i个负荷点的负荷功率,为简化运算,使用该负荷点的平均功率P代替,kW;tlp(i)为第i个负荷点的停电时间。
分别对不含储能系统和含储能系统的负荷点停电时间tlp(i)进行计算。
1)未接入电池储能系统,即x(i)=0时。
根据式(5)—(7)可得此时负荷点i的停电时间tlp(i)为:
tlp(i)=tstop(i)
(20)
2)接入电池储能系统,即x(i)=1时。
当储能系统容量可覆盖停电缺失电量时,若配电网成功切换至储能系统供电,系统不停电,在储能系统切换失败时停电时间需考虑转供电系统;当储能系统容量无法覆盖停电缺失电量时,即使成功切换至储能系统供电,仍会造成停电,但储能系统是否成功接入会影响系统的停电时间,因此,有:
(21)
式中:rESS为切换至储能系统的成功率,可用储能系统可靠性来表示;tfail(i)为储能系统接入失败时系统的停电时间;tsuc(i)为储能系统接入成功时系统的停电时间。tfail(i)、tsuc(i)的计算方法如式(22)所示:
(22)
式中EB(i)为第i个负荷点储能可放电量。
上述计算过程的流程图如图5所示。
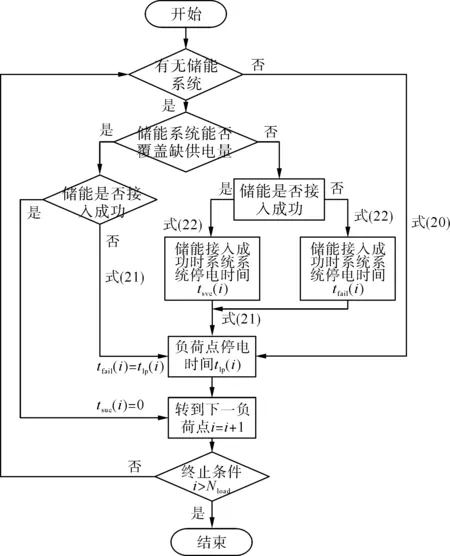
图5 负荷点停电时间计算过程Fig.5 Calculations of outage time of load point
3 实例分析
3.1 储能系统容量规划
以南方某工业园区配电系统为例建立上述模型,系统共有1 266个负荷点,模型参数值如表1所示,其中,参考行业标准,假设每个负荷点的用电功率为1 266个负荷点功率的期望值。由于本算例中部分负荷点未配备转供点,针对这些负荷点储能容量上限设置为E(i)max1,其余负荷点储能容量上限设为E(i)max2。

表1 优化模型参数Tab.1 Economic optimal model parameters
假设所有负荷点都有储能系统接入,在MATLAB上计算不同容量储能接入的经济成本以及对系统可靠性的影响。仿真结果如表2和图6所示。
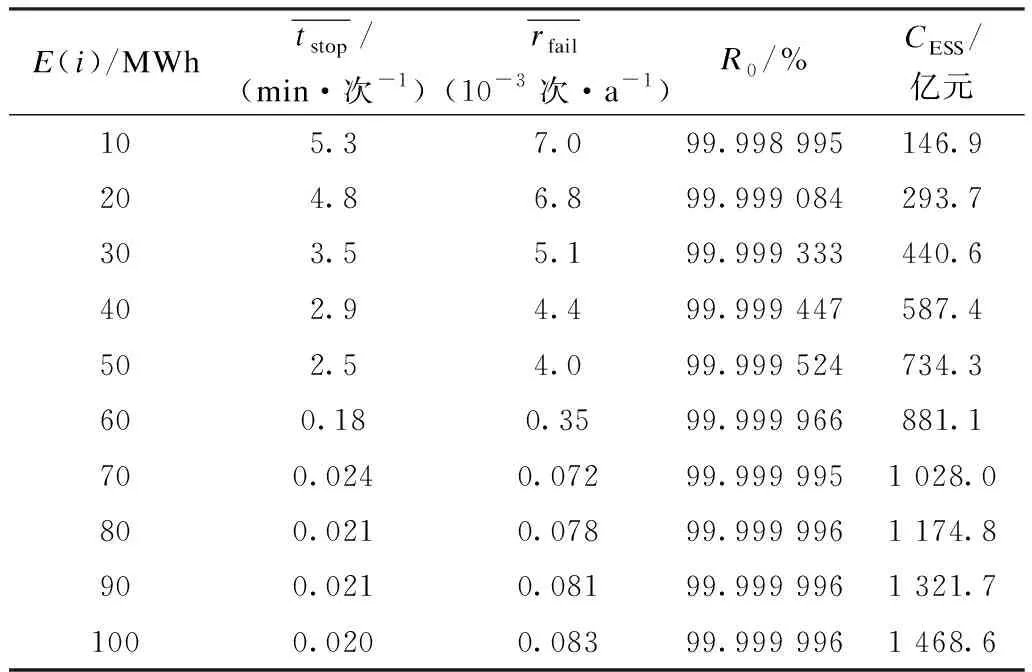
表2 不同容量储能全接入的仿真结果Tab.2 Simulation results of full access to different capacities of ESS
由图6可知,当储能系统的容量介于50 MWh和60 MWh之间时,系统可靠性提升较为明显;当容量超过60 MWh后,储能容量对系统可靠性的提升效果不明显,因此将储能的容量上限设置为60 MWh。但由于该配电系统负荷点数量多,实现储能系统的全覆盖所需成本过于高昂,因此需要在考虑经济性的条件下对储能系统的选址和容量分配进行优化。
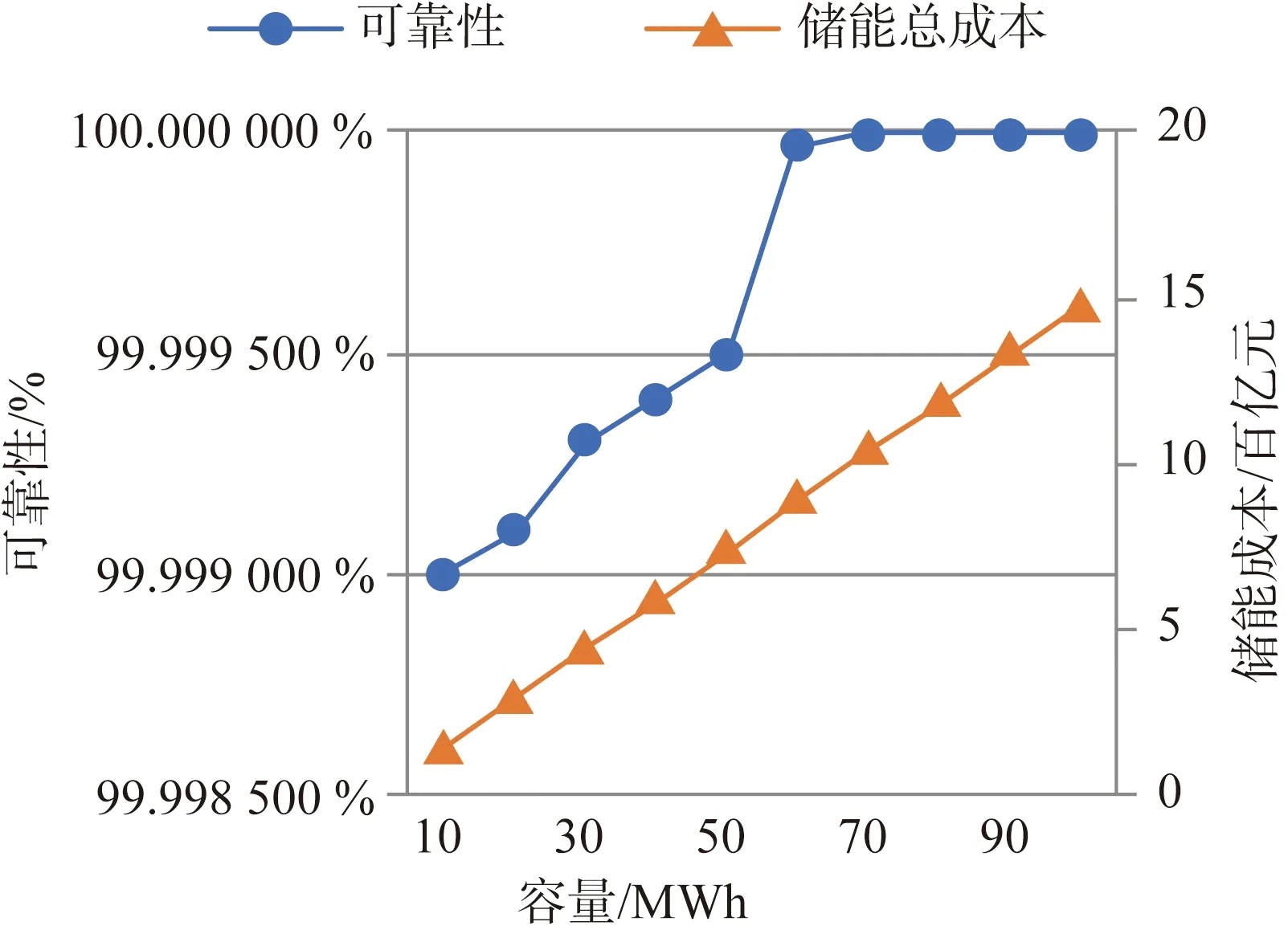
图6 不同容量储能全接入仿真曲线Fig.6 Simulation curves of full access to different capacities of ESS
3.2 储能系统选址定容联合规划
根据2.2节,经济性可靠性综合最优指标W是在经济性最优的基础上,使用模糊控制的思想建立成本和可靠性的统一评价标准,即通过隶属度函数将他们转化为统一的指标,随后通过权重系数反映可靠性和成本的权重。由于该目标函数是根据梯形隶属度函数加权所得,为了使可靠性指标和经济性指标有较明显的差异,宜合理选取隶属度函数参数a、b如表3所示,使得待评价对象评分指标均匀分布在分析区间,最后根据不同的权重系数对建立的模型进行优化仿真。

表3 隶属度函数参数Tab.3 Parameters of membership function
遗传算法是人工智能领域的一种搜索启发式算法,属于进化算法,这种启发式算法在解决复杂的组合优化问题时,能得到更快的优化结果,因此常被用来生成实际的优化和搜索问题的解,如:旅行航班优化、物流系统设计、生产调度等,基于可靠性的选址与定容优化模型的目标函数符合非线性、多模型、多目标等复杂系统优化问题的特点,可以利用MATLAB中的遗传算法工具箱进行优化[32]。同样以上述配电系统为算例,以经济成本可靠性综合最优作为目标函数进行优化,并对优化结果与经济成本最优为目标进行对照。
利用MATLAB中的优化工具箱“optimtool”中的遗传算法对储能系统的选址定容模型进行优化计算,为方便使用该优化工具箱,将式(14)改写为:
minW=-ωECOAECO(C)-ωRAR(R)
(23)
经过多次迭代寻优计算后,算法的收敛情况如图7所示。
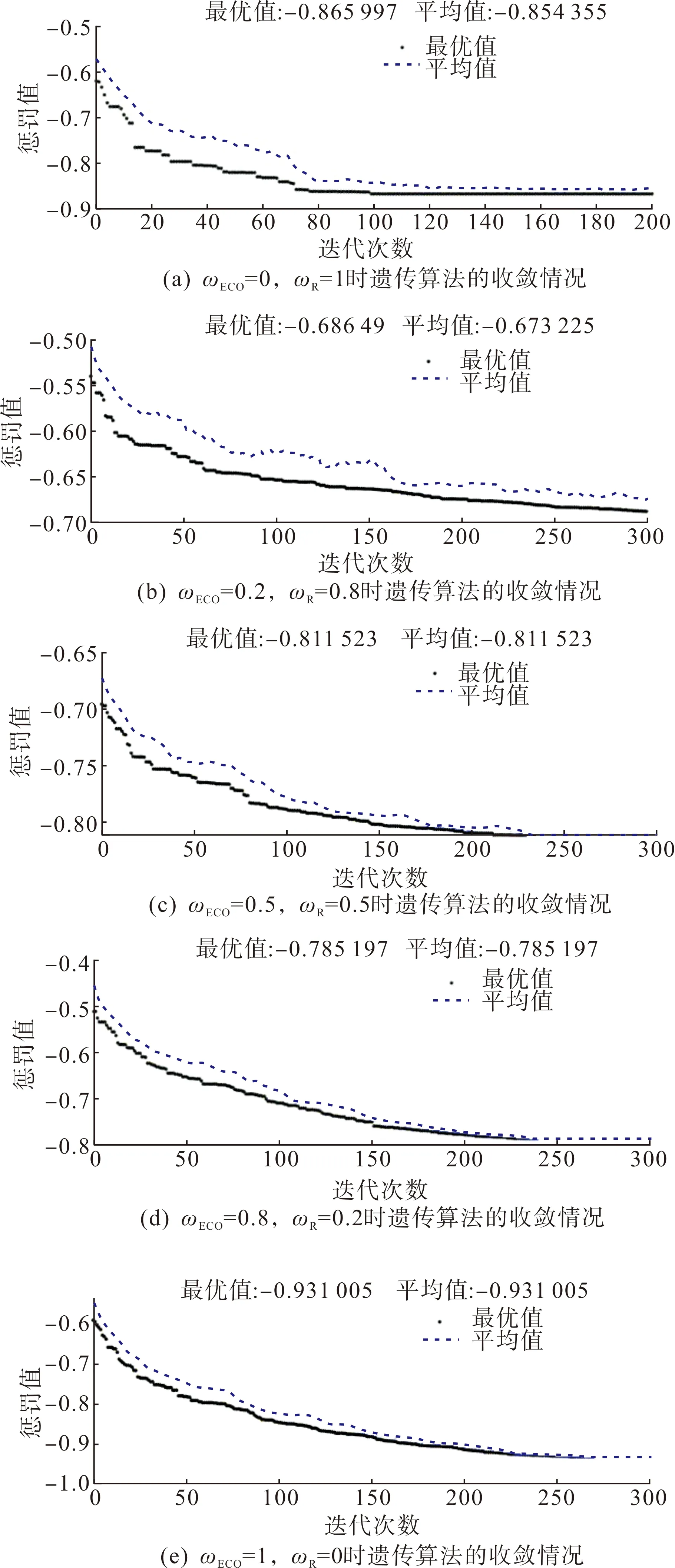
图7 遗传算法的收敛情况Fig.7 Convergence of genetic algorithm
将图5中的权重系数组合分别命名为“权重1”、“权重2”……“权重5”。对不同权重比例下储能接入的容量和接入点进行统计分析。经统计,考虑系统经济性的不同权重比例下的储能容量分布如图8所示。
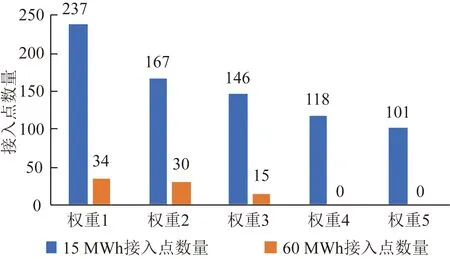
图8 优化容量统计(权重1~5)Fig.8 Optimize capacity statistics (weight 1~5)
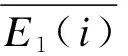
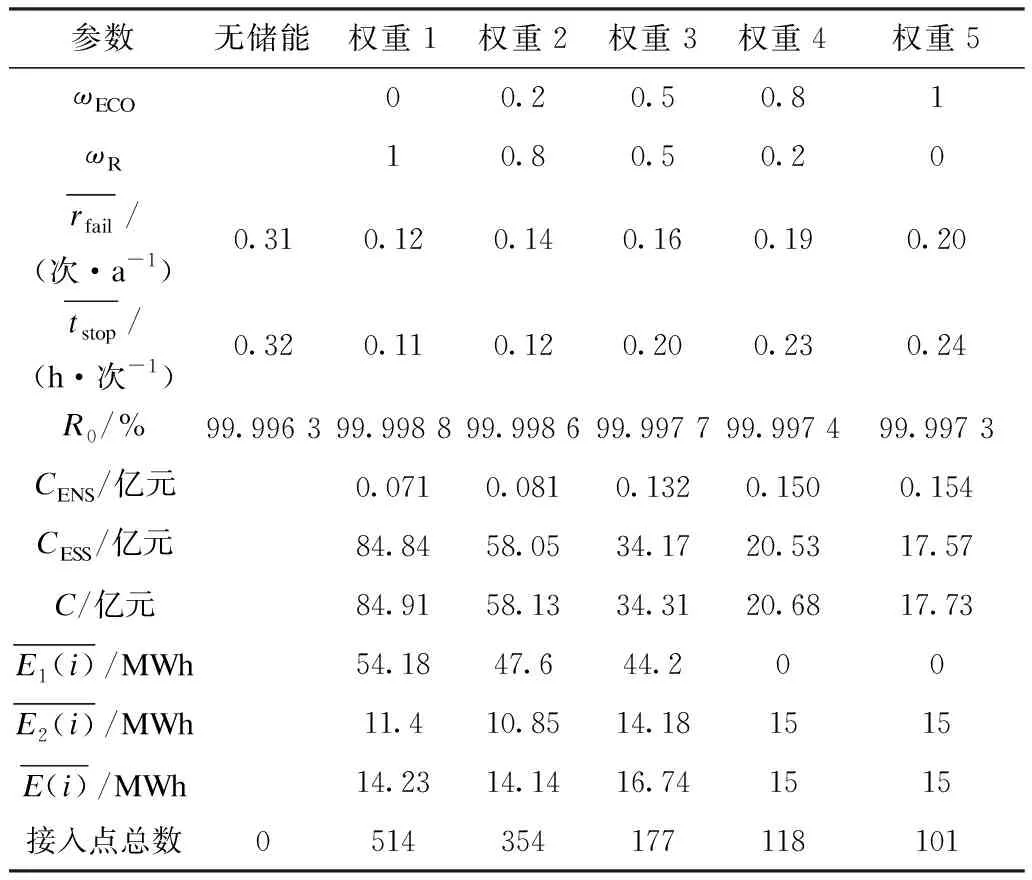
表4 是否引入储能系统的可靠性对比Tab.4 Reliability comparison with or without energy storage system
通过对图8和表4中的优化结果可知,当不考虑系统经济性时,在储能接入点不超过系统负荷点总数的80%为约束,优化结果建议在514个负荷点接入储能;与不安装储能的配电系统相比,系统可靠性提升了0.002 5%,平均停电时间减少12.6 min,下降了65.6%,效果明显,但是经济总成本达到84.91亿元,成本高昂。
为了进一步提高系统经济性,平衡系统可靠性与成本,逐步提高系统经济性指标权重,从图7的统计结果和表3的计算结果可知,一旦目标函数引入经济性指标,遗传算法会逐渐淘汰掉小容量储能,保留允许的最大容量。这是由于储能系统成本较高,随着经济性指标权重的增加,系统接入储能的数量和总容量逐渐减少,但对系统可靠性的影响较小,在权重5的影响下,系统可靠性提升0.001%,每次停电时间减少4.8 min,需要投入17.73亿元,具有较好的技术经济性。
综上所述,虽然目前建设储能系统的成本仍然较高,但是通过本文提出的考虑系统经济性和可靠性的储能的选址定容优化模型,可以为系统可靠性提升的储能建设提供规划指导意见,仍具有较大的工程实际意义。
4 结论与展望
本文主要研究了配电网的可靠性评估体系,采用解析法建立元件和系统的可靠性计算模型,分析了储能对提高配电网可靠性的影响。但由于现有储能电站存在成本高等问题,如何平衡可靠性与经济性的矛盾是未来储能电站规划需要考虑的重要因素。
本文利用遗传算法对经济性和可靠性综合最优的储能选址定容模型进行优化求解,并使用南方某工业园区配电系统作为算例分析,得出以下3点结论:
1)在不考虑经济性约束下给所有负荷点配置20 MWh的储能,能将系统可靠性由99.996 3%提升到99.999 1%,系统每次停电时间减少14.4 min,对可靠性提升效果显著,但是需要投资293.7亿元,成本过于高昂;
2)储能系统安装规模与系统可靠性成正相关,在接入点数量不超过80%、储能的容量不超过60 MWh的限制下,系统可靠性最多提升0.002 5%,此时只需要在40.6%的点接入平均容量为14.23 MWh的储能,系统每次停电时间减少12.6 min,对可靠性提升效果明显,但是经济总成本需要84.91亿元,成本较高;
3)经济性权重在0.2~1之间变化时,系统可靠性变化并不明显,在储能最低成本投入下,系统可靠性提升0.001%,每次停电时间减少4.8 min,需要储能成本17.73亿元,技术经济性较优。
未来风电、氢能、光伏等形式的新能源将实现大规模并网,考虑综合能源的配电网可靠性将迎来全新挑战与机遇,这也对配电网中储能电站的规划提出了新要求:可靠性评估还可以采用解析法与蒙特卡洛模拟结合的混合法,优化算法可以采用遗传算法或改进希尔伯特-黄变换方法。

