缓解网络阻塞的储能规划优化方法
龚贤夫,卢洵,刘新苗,周姝灿,陈鸿琳,程鑫
(1. 广东电网有限责任公司电网规划研究中心,广州510620;2. 广东电网有限责任公司,广州510620)
0 引言
随着社会经济的发展和城市化水平的提高,对电力的安全可靠供应要求也越来越高。然而受制于土地资源、环境保护等因素,负荷中心地区电网工程的建设往往存在投资造价高、施工难度大等问题,导致部分规划项目难以落地,产生网络阻塞问题。所谓网络阻塞是指由于电力网络本身容量的限制,不能满足所希望的供电计划的状态,主要是指系统在正常运行和事故状态下的线路或主变的有功越限情况[1]。储能的“移峰填谷”能力可将间歇式能源发电时在弃电时段的电能进行时空平移到非弃电时段,同时安装位置灵活[2 - 4],因此在理论上具备解决原有输配电线路或者变电站重过载的技术能力,降低电网工程建设困难和供电安全可靠要求之间的矛盾,从而起到缓解网络阻塞的作用[5]。
2017年,国家发改委、国家能源局等五部门联合印发了《关于促进储能技术与产业发展的指导意见》[6],明确了储能是提升传统电力系统灵活性、经济性和安全性的重要手段,要着力推进储能提升能源电力系统灵活性稳定性应用示范。此后,江苏、河南、湖南等一批百兆瓦级储能电站相继建成投产[7]。然而,目前电网侧储能仍存在应用价值难以量化评估、投资回报率低等一系列问题,随着《输配电定价成本监审办法》[8]的出台,要求储能设施不能纳入输配电价定价成本,电网侧储能项目由爆发式增长进入暂缓建设期。2019年,国家发改委、科技部等四部门进一步印发《贯彻落实<关于促进储能技术与产业发展的指导意见>2019—2020年行动计划》[9],强调要明确电网侧储能规划建设原则,规范引导电力系统储能健康有序发展。“电力建设,规划先行”,开展缓解网络阻塞的储能的规划方法研究具有现实意义。
关于储能应用规划问题,国内外研究机构已经取得了一定的成果。文献[10 - 13]针对大规模新能源的快速发展,提出了考虑储能的分层优化规划方法,将储能系统的规划问题和运行问题进行了有机结合,具有很好的启发性;另外,文献[14 - 16]针对配网和微电网的分布式光伏配置储能的配置、规划及风光储协同优化配置进行了研究并给出规划模型。文献[17]为弹性配电网规划了可移动式储能并进行优化。文献[18 - 19]针对台风等极端自然灾害对电力系统造成的危害,从提高电网抵御故障能力出发,研究了保证灾害中重要负荷不间断供电的配电网储能规划方法。文献[20]针对传统变电站扩建方式导致主变利用效率较低的问题,提出了一种缓解变电站扩建的储能运行方法,主要侧重于建立储能的经济运行模型。文献[21]以储能缓解电网负荷波动为背景,建立了储能的多目标优化模型。文献[22]针对区域供电线路故障会使部分线路出现短时拥塞导致的切机切负荷问题,研究了多功能复合储能优化配置方法,从功率需求和能量需求两方面进行了有益尝试。可以看出,目前的成果大多仍侧重于系统运行优化,如何将储能作为传统电网投资的替代方案,形成缓解网络阻塞的储能规划优化方法这一方面的研究还相对较少。
基于此,本文对缓解网络阻塞的储能规划优化方法进行了研究。首先根据负荷中心地区网络结构,按照“纵向梳理、横向整合”的方式将网络进行断面划分,针对各断面依次开展储能规划优化。其次,提出了缓解网络阻塞的储能规划优化模型,采用粒子群算法对模型进行求解,并制定了规划优化流程。最后,通过对粤港澳大湾区某负荷中心地区实际系统开展算例分析,与采用传统电网规划方案的效益进行对比,验证了本文所提方法的有效性,可为储能系统规划提供参考,并作为电网规划的补充和完善。
1 网络结构及断面划分
电网规划应遵循分层分区的原则,以确定网络的薄弱环节,避免投资的重叠和交错[23 - 24]。缓解网络阻塞的储能规划也应当坚持这一原则,明确投资方向,对症下药。根据各级电网存在的问题宜由本级电网规划解决的思路,有必要按照“纵向梳理、横向整合”对网络结构进行断面划分。
纵向梳理:即按照电压等级将网络结构“自下而上”进行断面划分,以实现上下电网储能优化的解耦。
横向整合:即将影响同一电压等级电网规划的影响因素进行整合,然后针对本级断面存在的问题进行储能规划优化研究。
以图1来简化表示负荷网络结构及断面划分方式。其中:A1为区域主供的500 kV变电站,A2为相邻供电区的500 kV变电站;B1、B2为区域主供的220 kV变电站,正常方式下合环运行,并通过A2—B2线路提供事故备用;C1为区域主供的110 kV变电站,正常方式下与C2开环运行,并通过线路C2—C1提供事故备用;D1为向用户供电的10 kV台区。图1所示的网络结构可分为3个断面:断面S1由C1变电站经过10 kV主干线路直接供电负荷中心地区D1;断面S2由B1变电站向主供断面S1的变电站C1提供电源;断面S3由A1变电站向主供断面S2的环网A1—B1—B2—A1提供电源。

图1 网络结构及断面划分简化示意图Fig.1 Simplified schematic diagram of network structure and power flow interfaces
按照“纵向梳理、横向整合”的规划思路,先针对断面S1进行研究,以确定是否需要以及需要配置何等规模的储能以缓解网络阻塞;然后针对断面S2进行研究,并将断面S1的规划成果作为边界条件进行更新,以确定断面S2需要配置的储能方案;依次类推,直至完成所有断面的储能规划优化配置。
2 缓解网络阻塞的储能规划优化模型
2.1 优化目标函数
从缓解网络阻塞的角度出发,为达到希望的供电计划,储能规划优化配置既要满足电力供应的安全性和可靠性,同时还应具备一定的经济性,否则采用传统的电网规划方法增加变电容量或线路输送能力以获取更高的效益。从不同角度出发储能的收益成本模式会有差异,为便于问题的研究,本文从全社会效益出发,综合现有研究思路,提出缓解网络阻塞的储能规划优化目标函数为:
(1)
式中:CES(X)为储能的投资与维护成本;CLoss(X)为系统阻塞成本;BES(X)为储能的充放电收益;G(X)为等式约束集;H(X)为不等式约束集。
为表述简便、清晰,本节所有目标函数及约束条件的相关变量及表述仅示意本级断面的内容,与上、下级断面在表述上不再区分。
X为储能规划优化模型的决策变量,有:
X=[pes,1,pes,2,…,pes,t,…,pes,T],∀t∈T
(2)
式中:pes,t为负荷高峰或低谷t时段储能充放电功率;T为时间周期。
上述目标函数中,储能的投资与维护成本与储能容量优化相关,属于规划问题;系统阻塞成本、充放电收益与储能充放电策略相关,属于运行问题。研究表明储能的规划与运行是相互影响的,统筹储能规划是为了保证系统正常运行,而储能运行过程中又可以影响到下一步储能设备的规划方面。
为统一时间尺度,根据储能的使用寿命计算CES(X)的年平均成本,此时决策变量X主要由负荷在高峰或低谷时段储能充放电功率pes,t所决定,放电时pes,t取正值、充电时pes,t取负值,模型中以年负荷时间曲线来计算储能的全寿命周期费用,进一步分析得到储能配置经济性优化结果。
储能的日投资与维护成本可表示为:
(3)
(4)
式中:EES(X)为优化的储能额定容量;PES(X)为优化的储能额定功率,根据储能充放电功率决策变量X求取,并作为规划优化模型的结果输出;γ为贴现率;n为储能使用寿命,a;Td为储能年运行天数;Cy为第y年储能固定投资成本;c1为储能系统单位容量成本,元/kWh;c2为储能系统运维成本,元/(kWh·a);c3为储能系统单位功率成本,元/kW。
系统阻塞成本可表示为:
(5)
(6)
式中:PL(X)为由储能充放电功率决策变量X计算得到的断面潮流;Pload,t、PG,t、Ploss,t分别为t时刻断面内负荷需求、电源出力和网损;Plim为断面潮流限值;m为时间周期T内断面潮流PL(X)>αPlim的窗口总数;Lj为第j个时间窗口单位停电损失费用;α为预控负荷比例(即调度运行允许线路或者主变控制的最高负载率),且α≤1。根据控制指标α来确定发生网络阻塞时,储能系统将断面潮流控制在多少负载以内。当储能规划优化目标函数与传统的电网规划方法计算结果相同时,可得到临界条件下的储能规划优化方案。
储能的充放电收益可表示为:
(7)
(8)

2.2 约束条件
等式约束集G(X)主要包括储能功率与容量约束、储能荷电状态递推约束、系统潮流约束等。其中储能功率与容量约束、储能荷电状态递推约束为:
(9)
PES(X)=max(pes,t),∀t∈T
(10)
(11)
式中:SSOCM、SSOCm分别为储能最大允许荷电状态、最小允许荷电状态;ΔT为1个放电(充电)周期的计算时段;Δt为计算时段时间间隔;Et为在t时刻的储能剩余容量。系统潮流约束属于常规约束条件,在此不再赘述。
不等式约束集H(X)主要包括储能充放电功率约束、储能荷电状态约束、节点电压约束、电源出力约束等。
-PES(X)≤pes,t≤PES(X),∀t∈T
(12)
SSOCm×EES(X)≤Et≤SSOCM×EES(X),∀t∈T
(13)
Uk,min≤Uk,t≤Uk,max,∀t∈T
(14)
Pg,min≤Pg,t≤Pg,max,∀t∈T
(15)
Qg,min≤Qg,t≤Qg,max,∀t∈T
(16)
0≤Pw,t≤Pw,t,pr+ΔPw,t,pr,∀t∈T
(17)
0≤Pv,t≤Pv,t,pr+ΔPv,t,pr,∀t∈T
(18)
式中:Uk,t、Uk,min、Uk,max分别为节点k在t时刻节点电压、电压下限、电压上限;Pg,t、Pg,min、Pg,max分别为发电机g在t时刻有功功率的出力、下限和上限;Qg,t、Qg,min、Qg,max分别为发电机g在t时刻无功功率的出力、下限和上限;Pw,t、Pw,t,pr、 ΔPw,t,pr分别为风电w在t时刻有功功率的出力、预测值和预测误差值;Pv,t、Pv,t,pr、 ΔPv,t,pr分别为光伏v在t时刻有功功率的出力、预测值和预测误差值。
2.3 临界储能规划优化方案的确定
在实际的电网规划过程中,决策者往往还希望知道在何种条件下,利用储能缓解网络阻塞和采用传统的电网规划方法增加变电容量或线路输送能力可以获得相同的目标函数,因此计算临界的储能规划优化方案具有现实意义。
以解决系统阻塞问题为导向,则系统阻塞成本是目标函数的主导因素,从式(5)—(6)可以看出,在不同预控负荷比例α下可得到不同的储能规划优化结果。α越小,阻塞潮流计算的起始点越低,优化得到的储能额定功率和额定容量越大;反之,则阻塞潮流计算的起始点越高,优化得到的储能额定功率和额定容量越小。根据这一条件,采用固定步长调整α进行数值计算,记传统的电网规划方法目标函数为ftrad,当ftrad处于相邻的α1和α2计算得到的储能规划优化目标函数值f(α1)、f(α2)之间时,即:
(19)
此时可用差值法近似计算临界预控负荷比例αcr。
(20)
然后再将αcr代入式(1)即可计算得到临界储能规划优化方案。需要注意的是,当取任一α时均有ftrad 如前所述,以式(1)为优化目标,并考虑相关约束条件后,本文所构建的储能规划优化模型利用储能“高放低充”特性,使得断面潮流限制在预控负荷内,解决网络阻塞的多决策变量经典优化问题。本文选择在电力系统优化过程中被广泛使用的粒子群算法[25]进行求解。 具体的规划流程如图2所示,步骤如下。 步骤1:按照负荷中心地区网络结构,自下而上划分N个断面,并令i=1。 步骤2:给定预控负荷比例α,设置阻塞潮流计算起始值;给定粒子群算法参数,初始化粒子群的位置和速度,根据粒子信息生成储能规划优化决策变量;更新潮流计算数据。 步骤3:计算各粒子目标函数值,更新个体最优解和群体最优解,更新粒子位置和速度;判断是否满足粒子群算法终止条件,若是执行下一步,若否则重复步骤3。 步骤4:生成储能规划最优决策变量,计算对应预控负荷比例下的储能规划优化方案;判断是否完成所有预控负荷比例下的储能规划优化,若是执行下一步,若否则调整预控负荷比例后执行步骤2。 步骤5:比较各预控负荷比例下的储能规划优化目标函数f(α)与传统的电网规划方法目标函数ftrad,判断是否存在f(α) 步骤6:若i 图2 模型求解方法及流程Fig.2 Solving method and process of the model 采用粤港澳大湾区某负荷中心地区电网进行算例分析。为增强算例的适应性,对网络结构进行了简化和假定,如图3所示。该地区负荷发展成熟,峰谷差较大,传统基建项目实施较困难,同时已有变电站内具备布置储能系统的地理条件。按照自下而上进行断面划分的思路,共划分为3个断面。 1) 断面1主要由110 kV站HZ-C2经10 kV F13支线供电(含1号变压器、2号变压器、3号变压器、4号变压器等)。根据电力需求预测,典型工作日高峰负荷为6.8 MW,区内无电源布局,该断面潮流限值为6.39 MW。 2) 断面2由220 kV站HZ-B3经同塔双回线路向C1-C2供电区供电,其中HZ-C1站为T接方式。HZ-C3—HZ-C2线路为HZ-C2站提供事故备用。根据电力需求预测,典型工作日高峰负荷为181.8 MW(含断面1负荷),区内含1座额定功率50 MW的热电厂HZ-S,该断面潮流限值为125 MW。 3) 断面3主要由500 kV站HZ-A1经HZ-A1—HZ-B3—HZ-B2—HZ-B1—HZ-A1环网供电,其中220 kV站HZ-B3通过HZ-B4—HZ-B3线路由相邻的500 kV站HZ-A2提供事故备用。根据电力需求预测,典型工作日高峰负荷为901.8 MW(含断面1、断面2负荷),区内主要电源为接入断面2的热电厂HZ-S,该断面潮流限值为1 180 MW。 图3 某负荷中心地区简化电网结构图Fig.3 Simplified grid structure of a load center 根据第3节缓解网络阻塞的储能规划流程,按照自下而上的方法,算例系统首先对断面1进行储能规划优化。搭建地区电力系统潮流计算模型,根据典型工作日电力需求数据以及电源出力数据,得到各时段断面1潮流曲线如图4所示。从图中可以看出,在14:00—17:00、19:00—21:00时段断面潮流均超过热稳极限。 图4 典型工作日断面1潮流曲线Fig.4 Power flow of interface 1 at typical workday 表1给出了算例使用的锂电池系统参数,表2给出了不同时间窗口下的停电损失费用[26]。 表1 电池储能参数Tab.1 Parameters of the battery energy storage 表2 单位停电损失费用Tab.2 Unit loss cost caused by power failure 峰谷电价的执行标准为:1)高峰电价为1.040 3元/kWh,高峰时段为14:00—17:00、19:00—22:00;2)平段电价为0.630 5元/kWh,平段时段为08:00—14:00、17:00—19:00、22:00—24:00;3)低谷电价为0.315 3元/kWh,低谷时段为00:00—08:00。优化过程中设置粒子数为20个,最大迭代次数为400次,取α为95%~100%时,得到断面1的储能规划优化方案及其目标函数如表3所示。每个α值下重复5次以上的寻优操作,结果均能稳定准确地收敛到表3结果附近,说明粒子群算法对本文所提模型具有良好的适用性。 表3 不同α值下储能规划优化结果Tab.3 Optimization results of energy storage planning under different α 从表3的优化结果来看,当α最小时,阻塞潮流计算的起始点为6.07 MW,此时阻塞潮流计算的起始点较低,为降低系统阻塞成本,储能优化的结果倾向于配置更高规模的功率和容量,因此其目标函数最大;当α为1时,阻塞潮流计算的起始点即为断面极限6.39 MW,储能配置结果较小,此时系统按照100%的潮流控制断面,储能优化的结果倾向于配置相对较低规模的功率和容量,因此其目标函数最小。 根据地市供电局电网规划的成果,由于该断面属于城市中心成熟居民和商业区域,新建架空线路难度很大。据测算新建设一回长度为5.9 km、截面积为300 mm2的10 kV电缆线路投资总额约693万元,按照25 a运行期并考虑年2.5%的运维成本后,投资等年值约73.3万元/a,据此传统电网规划方案目标函数为ftrad=2 538.9元/d。 利用式(19)—(20),取α1=97%和α2=96%进行计算,得到αcr=96.6%。并将αcr值重新代入式(1)进行优化,得到临界规划优化方案,其中储能额定功率为0.93 MW、额定容量为4.30 MWh,目标函数为2 536.2元/d,与传统电网规划方案基本一致,说明采用差值法近似计算在工程上可行。临界储能规划优化方案下的断面1潮流和储能充放电功率曲线如图5所示,粒子群算法收敛曲线如图6所示。 从图5—6可知,断面1配置储能缓解网络阻塞的最小规模为0.74 MW/2.64 MWh,临界规模为0.93 MW/4.30 MWh。 图5 临界方案下潮流优化曲线及储能充放电功率Fig.5 Power flow and charging and discharging power of energy storage under critical scheme 图6 算法收敛曲线Fig.6 Convergence curve of the algorithm 根据储能规划流程,对断面2进行储能规划优化配置时,需将断面1的储能规划优化配置方案作为边界条件。此处以临界储能规划优化方案进行潮流数据更新,由此得到典型工作日各时段断面2潮流曲线如图7所示。在09:00—12:00、14:00—18:00两个时段断面潮流超过热稳极限。 图7 典型工作日断面2潮流曲线Fig.7 Power flow of interface 2 on typical workday 利用4.1节相关参数,取α为100%时,对断面2的储能规划方案进行优化,得到储能额定功率为16.8 MW、额定容量为77.8 MWh,目标函数为55 674.4元/d。如采用传统电网规划的方式,新建一回长度为12 km、截面积为630 mm2的110 kV电缆线路,按照粤港澳大湾区电缆造价控制线,则投资总额约6 864万元,按照25年运行期并考虑每年2.5%的运维成本后,投资等年值约为726万元/a,据此可得传统电网规划方案目标函数为ftrad=34 622.7元/d。 根据上节的优化结果分析,当α<100%时目标函数值均大于55 674元/d,即取任一α时均有ftrad 与4.2节类似,对断面3进行储能规划优化配置时,需将断面1、断面2的规划优化方案作为边界条件更新潮流计算数据,从而得到典型工作日断面3各时段的潮流曲线,如图8所示。从图中可以看出,断面3供电能力较强,高峰负荷时刻仍存在一定的裕度,因此暂无需对断面3进行储能规划优化配置。 图8 典型工作日断面3潮流曲线Fig.8 Power flow curve of interface 3 on typical workday 综合以上分析,算例系统用于缓解网络阻塞的的规划方案对比结果如表4所示。建议断面1内配置容量为0.74 MW/2.64 MWh~0.93 MW/4.30 MWh的储能,断面2、断面3则不建议配置储能。 表4 算例系统缓解网络阻塞的规划方案对比Tab.4 Comparison of the planning schemes to alleviate network congestion in different cases 本文提出了缓解网络阻塞的储能规划优化方法,通过对粤港澳大湾区某负荷中心实际系统的算例分析,得到以下结论。 1)为确定网络的薄弱环节,避免投资的重叠和交错,应坚持电网分层分区的原则,采用“纵向梳理、横向整合”的方式进行断面划分,并逐步研究各断面储能缓解网络阻塞的规划优化方案。 2)构建的储能规划优化模型综合考虑了储能的投资与维护成本、系统阻塞成本以及储能充放电收益,将规划问题和运行问题运行了整合。应用粒子群算法进行了求解,结果表明算法可对本文所提模型进行有效优化。 3)现有投资造价情况下,利用储能缓解网络阻塞的效益相对偏低。对于中低压配网,当阻塞潮流设置点较高时,可以考虑建设储能系统;对于高压配电网及输电网,则优先考虑建设传统电网项目。建议现阶段优先以中低压配电网为主开展示范应用研究。3 模型求解方法及规划流程

4 算例分析
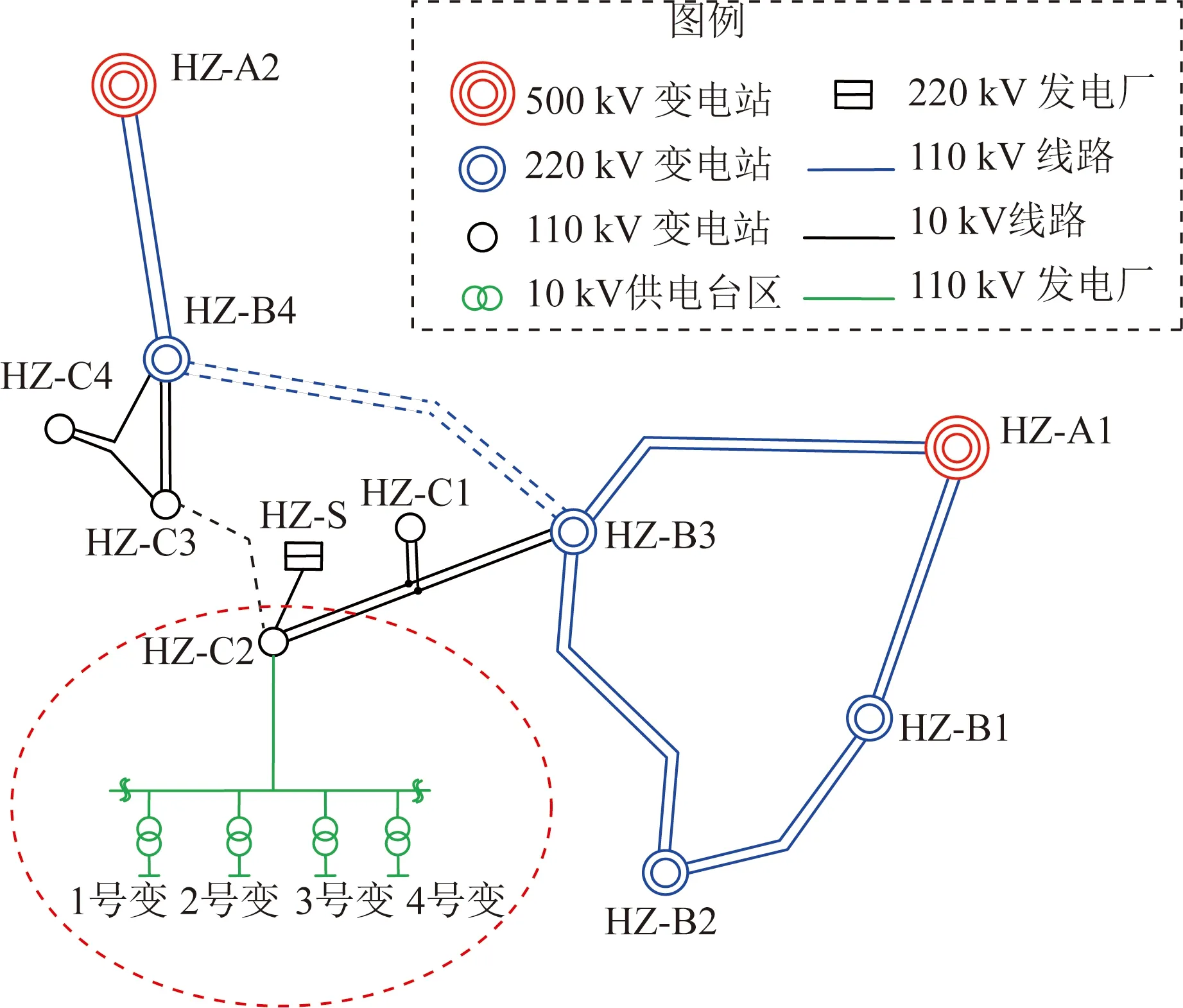
4.1 断面1储能规划优化方案






4.2 断面2储能规划优化方案

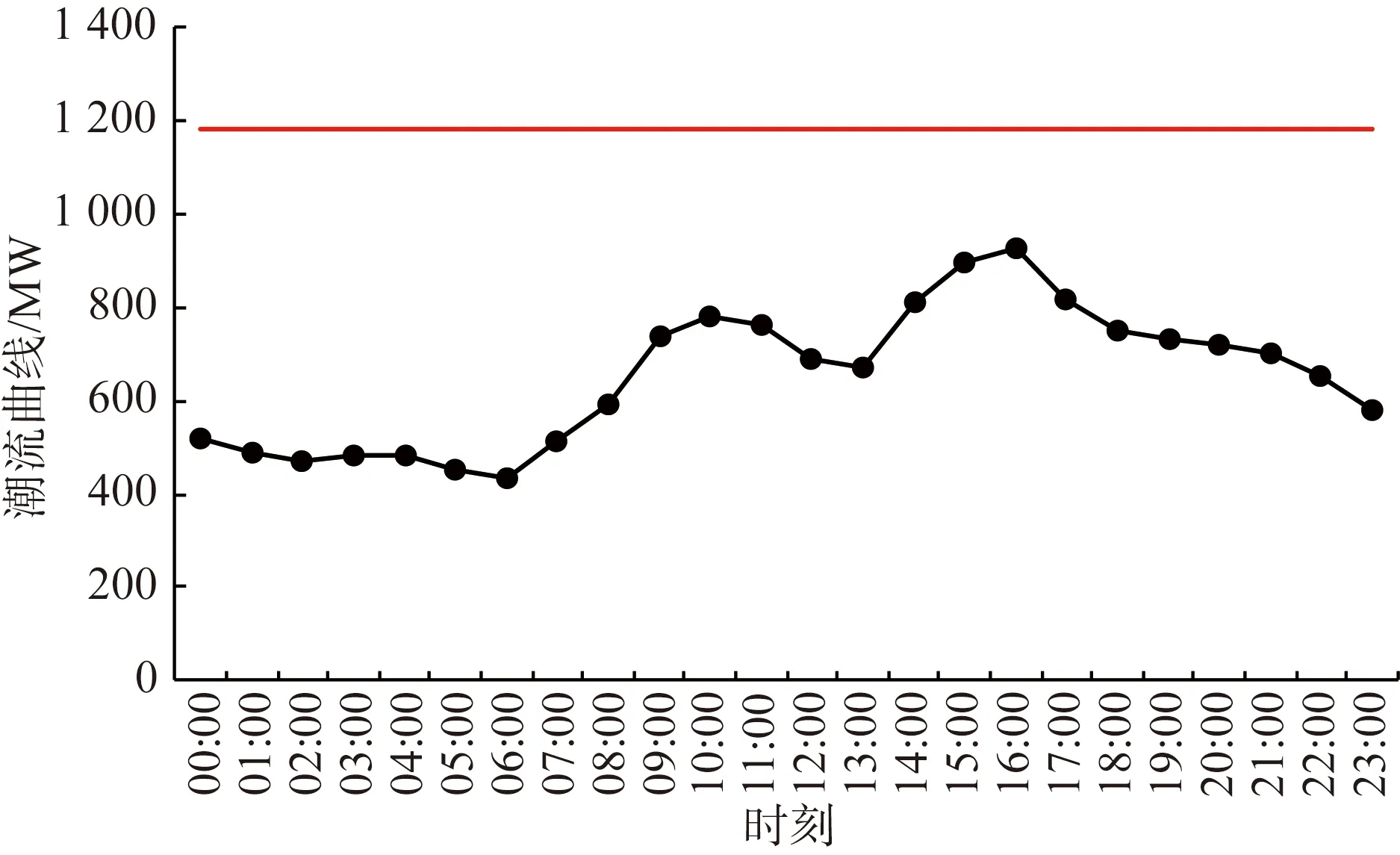
4.3 断面3储能规划优化方案

5 结论

