一种应用于换热网络综合的阻尼优化方法

刘薇薇，崔国民，张璐，肖媛，杨其国，张冠华

（上海理工大学能源与动力工程学院，上海市动力工程多相流动与传热重点实验室，上海 200093）

引 言

换热网络通过使用多个换热设备将工艺物流加热或冷却达到目标温度，实现最小投资费用或最大能量回收，其优化理论的研究对节能减排、降低能源损耗具有实际工程应用意义，为实现“碳达峰”和“碳中和”的目标提供解决方案。但换热网络综合为复杂的混合整数非线性规划问题，其中以结构为主的整型变量是影响换热网络目标函数非凸非线性的主要因素，而换热单元的布置与结构多样性对扩大换热网络的搜索域起着关键作用，因此开发高效的结构优化技术对提升换热网络全局优化性能具有重要意义。

自Masso 等[1]提出换热网络优化问题以来，众多学者致力于优化模型和算法的改进以获得年综合费用更低的换热网络结构。Yee 等[2-3]基于同步优化思想提出了分级超结构模型(SWS)，研究者们[4-6]从换热器串联和旁流结构的生成、有分流SWS 模型的拓展以及公用工程灵活布置等提高结构多样性的角度改进SWS 模型，进一步扩充了求解域；Xiao 等[7]和徐玥等[8]提出的节点非结构模型在结构匹配上更加灵活，随之将非结构扩展模型应用于有分流换热网络，并结合节点配置策略对流股的分支数和分组数进行动态调整，提高了模型的求解效率。常见的启发式方法有模拟退火算法(SA)[9]、微分进化算法(DE)[10]、粒子群算法(PSO)[11]、遗传算法(GA)[12]、强制进化随机游走算法(RWCE)[13]等，因其进化机制简单、搜索能力强等特点被广泛应用于换热网络问题的求解[14-16]。在此基础上，研究者们侧重对算法的执行方式或者内部结构进行改进，Pavão 等[17]在SA 的基础上提出一种新型火箭烟花优化策略，有效提升了算法优化性能；Aguitoni 等[18]将SA 与DE 结合的混合算法可同时兼顾对换热网络拓扑结构的优化和连续变量的优化；Thuy 等[19]将DE 与夹点技术相结合，在夹点处进行分流，用DE 确定换热单元的热负荷及分流比；王世豪等[20]基于离散PSO 和模拟退火思想提出双层优化策略，对网络结构和换热器面积进行同步优化；陈帅等[21]综合单层算法和传统双层算法的不足，提出抽样平均近似的改进PSO 算法应用于无分流换热网络综合；Rathjens 等[22]提出基于GA 的结构识别和参数改变的局部优化策略简化了换热网络结构，提升了局部搜索能力；Feyli等[23]提出一种基于GA 和修正的拟线性规划模型耦合的有分流换热网络综合方法。RWCE算法在分级超结构模型以及节点非结构模型中的应用体现出了其良好的优化性能，其中在算法关键优化参数上的改进[24-25]可更好地兼顾整型变量与连续变量的优化；在结构摄动方面加入换热单元重构策略、结构融合策略等操作[26-28]可有效提升结构进化能力。上述研究对算法的改进虽具有一定效果，但由于算法的贪婪性，在对问题求解时总是选择接受当前最优解，并未从全局最优上加以考虑，难以避免陷入局部极值，而RWCE 算法中的接受差解机制虽在一定程度上可有效跳出局部极值，但在优化后期接受差解的同时也破坏了具有潜力结构的优化路径，算法的优化性能仍有待进一步提升。

鉴于此，通过分析换热网络固化结构的成因及当前接受差解机制对优化的影响，基于结构延缓的思想提出一种阻尼优化方法应用于有分流节点非结构模型。将延缓概率引入结构继承机制中，以一定概率不接受当前最优解，延缓固化结构的形成；在此基础上，进一步提出分阶段延缓策略，通过调控在不同优化阶段的延缓概率，使得网络结构进化能力得以提升，以此提高全局搜索能力；最后采用四个不同规模的换热网络算例验证阻尼优化方法的有效性。

1 换热网络优化数学模型

1.1 有分流节点非结构模型

采用有分流节点非结构模型（nodes-based nonstructural model with stream splitting, NNM-SS）优化换热网络，以节点的形式量化换热器的位置，换热匹配的产生不受级数的限制，且节点数及分流数的设置更具灵活性。图1 表示4SP 算例的NNM-SS 结构示意图，节点参数包括分支数、分组数以及分支上节点数，冷热节点间连接表示换热器，分别在热、冷流体末端设置冷、热公用工程辅助换热使流体末端出口温度达到目标温度，用©、Ⓗ表示。图中共包含4 个换热器，Q表示换热器的换热量，初始节点参数设为：热流股分支数nfH=2，分组数ndH=3，分支上节点数mdH=2；冷流股分支数nfC=3，分组数ndC=3，分支上节点数mdC=2。

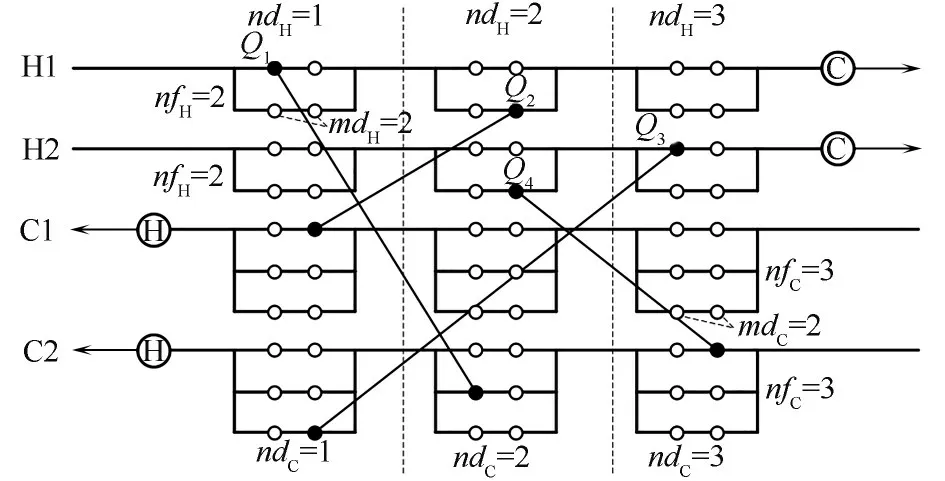
图1 有分流节点非结构模型示意图Fig.1 Structure of nodes-based non-structural model with stream splitting

1.2 目标函数

以最小年综合费用（total annual cost,TAC）为换热网络优化目标，目标函数如式(1)所示，包括运行费用和投资费用，其中前三项为换热单元的固定投资费用和面积投资费用，后两项为冷、热公用工程的运行费用。

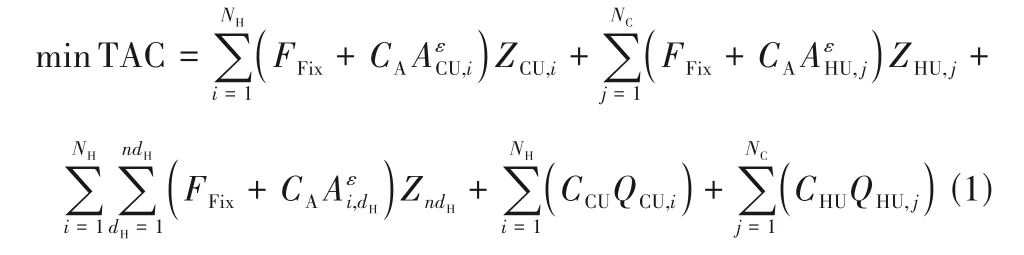
式中，FFix为固定投资费用；CA为面积费用系数；Z为换热单元是否存在的0-1 变量；ε为面积费用指数；CCU、CHU分别为冷公用工程、热公用工程的费用系数；QCU、QHU分别为冷公用工程、热公用工程换热量；Ai,dH、ACU,i、AHU,j分别为换热器、冷公用工程、热公用工程的换热面积；NH、NC分别为热、冷流体流股数。

1.3 约束条件

约束条件主要包括换热匹配中冷热流体的热平衡约束、换热单元的进出口温度约束、公用工程温度约束以及冷热分流比约束。

（1）换热器热平衡

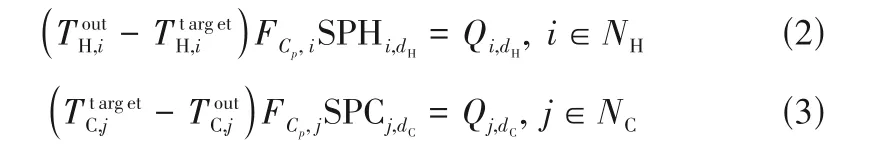
（2）公用工程热平衡

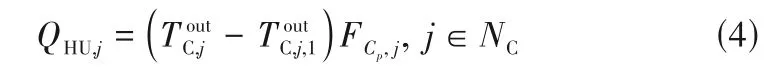
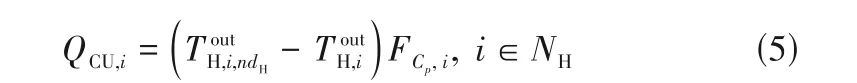
（3）流股热平衡

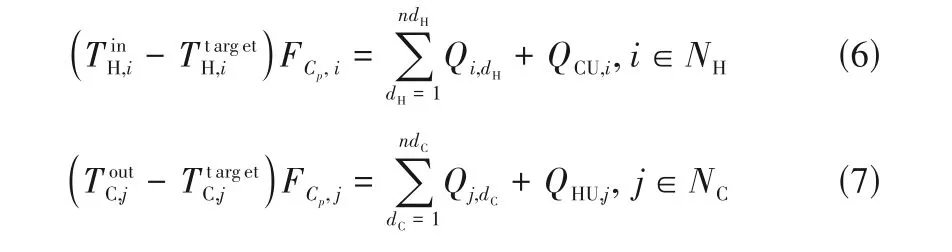
（4）最小温差约束

模型中最小传热温差ΔTmin均取值为0℃，以保证换热面积和换热量非负。

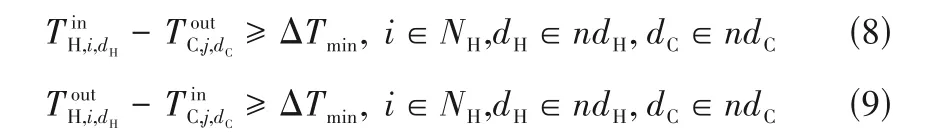
（5）流股分流比平衡

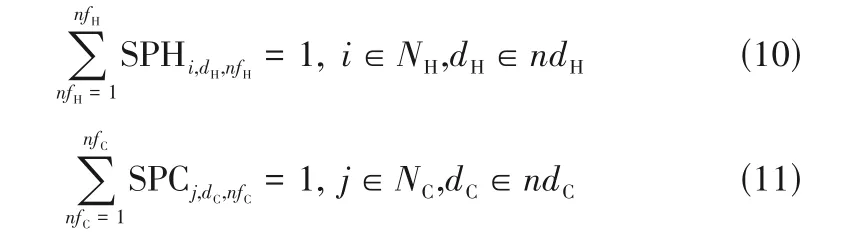
2 换热网络优化的局限性分析

2.1 RWCE算法优化有分流换热网络

RWCE 算法在优化过程中所有个体均独立进化，个体之间没有相互交流，其接受差解机制的设置可以强制跳出局部最优解，提升全局优化性能。RWCE 算法经过验证是较为高效的优化算法，将其应用到有分流节点非结构模型中优化换热网络，主要优化流程见图2。

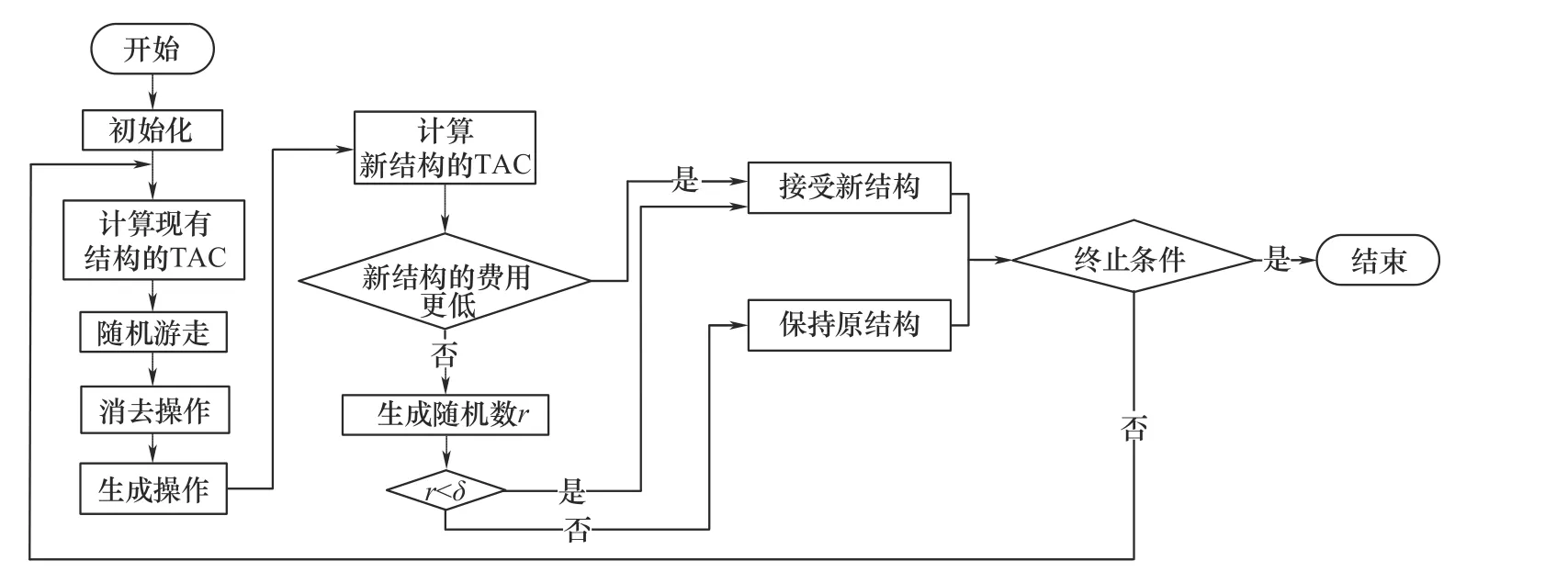
图2 RWCE算法优化流程Fig.2 Flow chart of RWCE algorithm

其中，r为0～1之间均匀分布的随机数，δ为接受差解概率，在随机游走进化过程中对换热器的换热量以及冷、热分流比随机更新，如式(12)～式(14)所示：

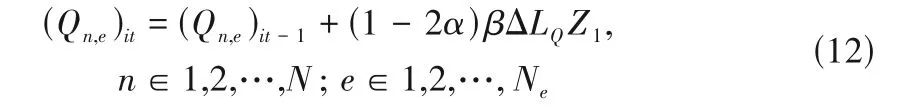
2.2 接受差解机制对优化的影响分析

RWCE算法的接受差解机制是以一定概率接受一部分费用较高的结构，给予较差的结构充分发挥其优化潜力的机会，可避免算法陷入局部极值难以跳出。以15SP 算例分析在不同优化阶段在接受差解过程中年综合费用的变化趋势，该算例包括8 股热流和7股冷流，物流数据参见文献[29]。

算法优化参数设置：ndH=ndC=3，nfH=nfC=2，mdH=mdC=1，δ=0.01，ITmax=1×108。对优化进程进行监测，观察每股热流上换热单元热负荷变化以及年综合费用变化趋势。迭代从30 万步至8230 万步最优个体的年综合费用仍未发生变化，优化始终陷入停滞状态，因此图3 仅给出迭代到100 万步时当前解和历史最优解的变化曲线。在优化初期费用波动较大，是由于模型初始为空结构，可生成换热结构的空间充足，换热单元的生成与游走可引起年综合费用的大幅度下降；而在达到局部最优后，接受差解可强制结构变异，实现年综合费用的再次突破。迭代至20 万步时，接受差解后的费用在短暂的升高后，经过一段时间优化又回到了原有结果，且优化过程中多次出现费用突增现象，是因为接受的差解结构中若存在反向公用工程或者温度交叉将引起对该结构的惩罚，导致费用剧增且逐渐偏离优化方向。由此说明，一旦网络结构形成稳定的换热匹配，即使接受差解也难以形成有效的结构变异，而基于算法自身的优化又难以使当前结构发生变化，导致算法过早陷入停滞状态且优化结果较差。

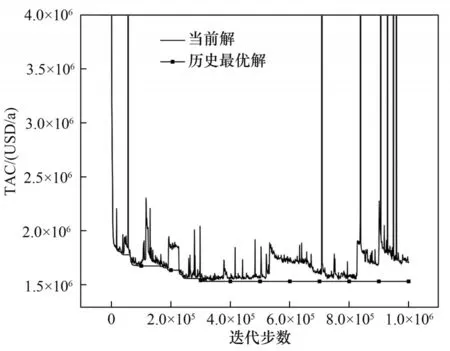
图3 当前解及历史最优解的费用变化曲线Fig.3 Cost variation of current solution and historical optimal solution

3 阻尼RWCE算法的提出

通过上文的探讨分析，接受差解机制具有两面性，在优化前期可使结构强制跳出局部极值，进而快速达到较优结构；但在优化后期多数被接受的差解会重复优化到原结构，难以形成有效的结构变异。对当前的结构优化机制进行调整，改变算法的执行方式是避免过早形成固化结构的可行方法。基于此，提出以结构延缓策略为核心的阻尼RWCE 算法，在优化过程中以一定概率不接受好解，延缓结构形成最佳匹配，给予充分的时间使有潜力的结构进行优化。优化过程中的延缓机理如图4 所示。

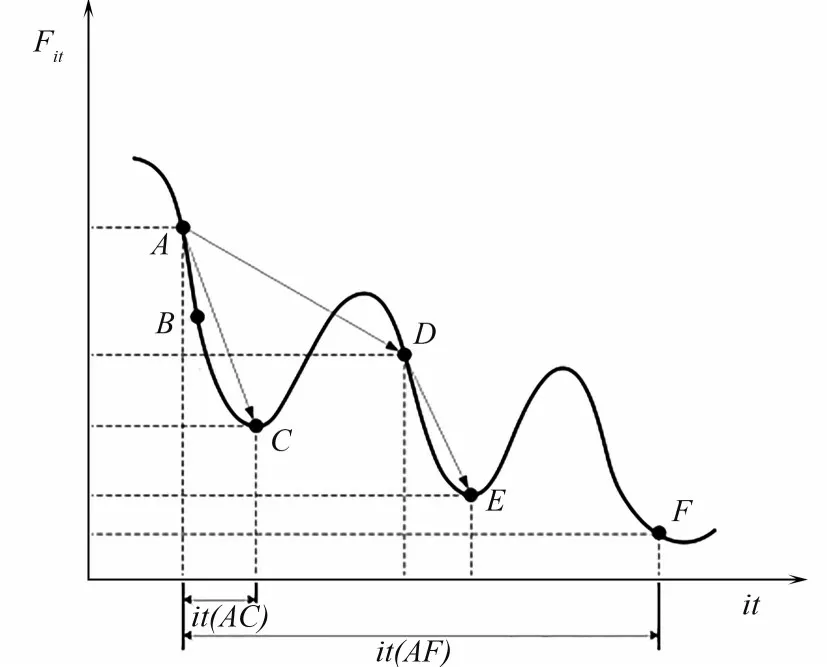
图4 TAC优化过程中的延缓机理Fig.4 Delay mechanism in TAC optimization

以图4 中曲线代表目标函数的优化过程，曲线A-F代表优化方向，C、E、F代表求解过程中可能存在的局部极值点。从A点开始优化，由于启发式算法的贪婪接受原则，易陷入局部极值点C，费用难以进一步下降；而接受差解机制以一定概率接受比C点费用高的解，优化方向从A-C变为A-D-E，跳出局部最优，但多次迭代后仍会返回原结构，费用难以进一步下降。

阻尼RWCE 算法的延缓机理：（1）延缓从A点搜索到局部极值C点的优化过程，以一定概率η（延缓概率）不接受优化过程中费用降低的结构，避免优化过早搜索到局部极值；（2）在不满足延缓条件时，选择以一定概率δ（接受差解概率）接受A-B过程中的任一结构，实现对更多优化路径的探索，从而增大可行优化方向；（3）在优化换热网络这类具有非凸非线性特点的问题时，在可接受的优化时间内，延缓策略可扩大搜索域有效跳出局部极值获得更优结构，从而提升全局优化能力。

3.1 结构延缓策略

结构延缓策略(DS1)是指在个体选择阶段改变结构继承机制，采用概率性接受好解作为下次迭代初始结构，同时采取结构保护机制，若当前结构对应的年综合费用相比上次迭代有所降低便不接受差解。具体操作为：若个体随机游走后的结构和上一步迭代的最优结构相比费用降低，则以一定的概率η不接受该结构，否则将游走后的换热量(Qn,e)it作为下次迭代的初始换热量，同时将游走后的结构以及分流比传递给初始结构；若费用相比没有降低，则下一步迭代的初始换热量依然为(Qn,e)it，而且以一定的概率δ接受差解，将(Qn,e)it作为下次迭代的初始换热量。

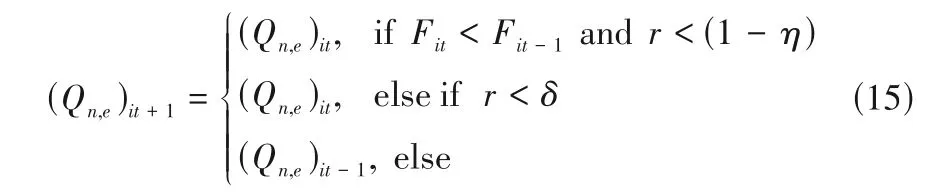
3.2 分阶段延缓策略

以一定概率不接受好解，使结构中换热单元匹配不过快达到饱和，延缓稳定结构的形成，采取延缓策略对延缓结构固化具有一定的效果。但是在优化过程中若全程采用相同的延缓概率，可能会使优化方向偏离路径从而错失好解。因此，提出分阶段延缓策略(DS2)，根据不同优化阶段搜索能力的差异，设置不同的延缓概率。在优化前期，设置相对合适的延缓概率，避免因连续变量变化过快形成固化结构；在优化中期，结构逐渐稳定，此时应降低延缓概率；在优化后期，结构已基本稳定难以再次变异，此时不延缓，保护好解使连续变量得到充分优化。具体操作为：

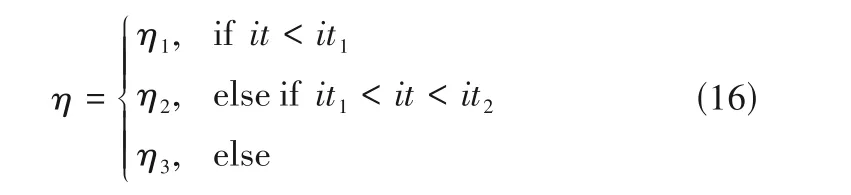
阻尼RWCE 算法的优化流程如图5 所示，其中分阶段延缓策略的延缓概率η按式(16)取值。

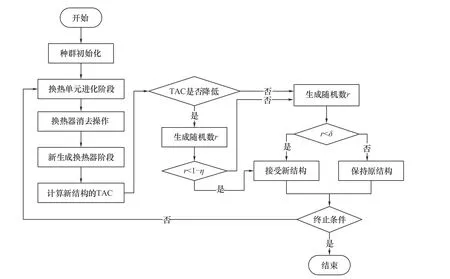
图5 阻尼RWCE算法优化流程Fig.5 Optimization process of DS-RWCE

3.3 延缓概率的取值及影响效果分析

采取延缓策略可有效防止优化陷入局部极值点，使换热匹配不过快达到稳定状态，以获得更优质的结构，其中延缓概率表示对好解的延缓程度，其取值大小对结构的优化有一定的影响。

图6(a)为在不同延缓概率下全程采用相同的延缓效果时年综合费用下降曲线，以延缓概率取0、0.2、0.4、0.6、0.8 为例说明不同的延缓力度对优化进程的影响。延缓概率为0，即采用基础RWCE 算法进行优化，迭代至2×108步时算法已基本停滞。在优化前期(0, 1.6×108)，延缓概率取0.2、0.4、0.6 时优化结果相比不延缓的结果偏低，且延缓概率取0.4优化结果下降趋势更为明显；优化中期延缓概率取0.2时结构优化性能进一步提升，取得了更低的年综合费用。延缓概率过大时，接受的好解较少，相应地接受差解较多，对结构的扰动较大，不利于结构优化；而延缓概率过小时，对易形成固化结构的延缓力度较弱，优化后期的结构仍会过早达到换热饱和，费用难以下降。

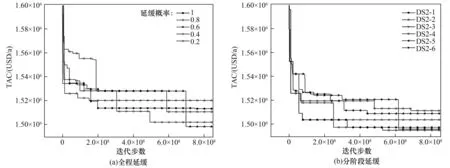
图6 不同延缓概率下的费用变化曲线Fig.6 Cost variation curves under different delay probabilities

图6(b)为在不同优化阶段设置不同的延缓概率其TAC 的变化，通过图6(a)不同延缓概率在不同优化阶段优化性能的对比，分阶段延缓概率在优化前期分别取0.2、0.4、0.6；在优化中期取0.2；在优化后期以0.2 的延缓力度或者不延缓进行优化，对应的结果如表1所示。由图可知分阶段延缓策略相比全程延缓费用均有所降低，通过调控在不同优化时期的延缓概率，可以促进结构进一步优化从而获得更低的年综合费用。其中情况4 对应的结果最低，结果为1495453 USD/a，情况3 和情况4 在第一阶段和第二阶段延缓概率取值相同，情况3 在第三阶段依然以0.2的概率进行延缓；而情况4在第三阶段延缓概率取为0即不进行延缓，对应的年综合费用更低。因此，在优化后期结构已基本稳定难以再突破结构变异时，不进行延缓能够保护好解，使连续变量得到充分优化，得到更优解。

表1 分阶段延缓策略在不同优化阶段延缓概率的取值Table 1 Values of delay probability of phased delay strategy in different optimization stages

4 策略有效性分析

4.1 算例1

算例1 为9SP 算例，包括4 条热流股和5 条冷流股，换热器费用为2000+70AUSD/a，热公用工程单位费用为60 USD/(kW·a)，冷公用工程单位费用为6 USD/(kW·a)。该算例最早由Linnhoff 等[30]提出，后续许多学者使用此算例进行换热网络模型及优化算法的验证，Fieg 等[31]将多种优化策略加入遗传算法，得到了优化结果为2922298 USD/a 的有分流结构；霍兆义等[32]将有分流并联结构和无分流串联结构引入换热网络优化模型，并采用遗传算法和粒子群算法结合的双层优化算法对模型求解，得到的优化结果为2922585 USD/a。孙涛等[25]提出大步长激励促进结构进化，进一步提升了网络结构的进化能力，获得了2920246 USD/a 的优化结果。鲍中凯等[33]允许公用工程布置在结构内部的各流股分支上，从而得到了2906286 USD/a的最优结果。

本文基于有分流节点非结构模型采用RWCE算法对换热网络进行优化，初始节点参数设置：ndH=ndC=6，nfH=nfC=2，mdH=mdC=1，延缓概率的取值如表2 所示。优化到2000 万步时算法陷入停滞，初步优化得到的结果为2898422 USD/a(图7)。将延缓策略应用于RWCE 算法，采用全程延缓策略（DS1）得到了TAC 为2893376 USD/a 的有分流换热网络结构；采用分阶段延缓策略（DS2）得到的最优结构如图8 所示，优化结果为2892210 USD/a。相比基础RWCE 算法费用降低了6212 USD/a，是由于采用延缓策略可以多次跳出局部最优解，延迟固化结构的生成，增强了结构的多样性。与文献中最优结果对比如表3 所示，可看出采用延缓策略的优化结果均低于已有文献结果。其中图8 的结构和文献[33]相比年综合费用降低了14076 USD/a，虽然图8 换热单元数有所增加且在多条流股上生成了分流结构，提高了换热器的面积费用和投资费用，但是增加了换热器，H4 流股和C5 流股上的公用工程需求量相应减少；此外在C1流股上存在内部热公用工程与一条分流进行换热，提升了该流股上的换热潜能，降低了公用工程的面积费用，获得了费用更低的网络结构。

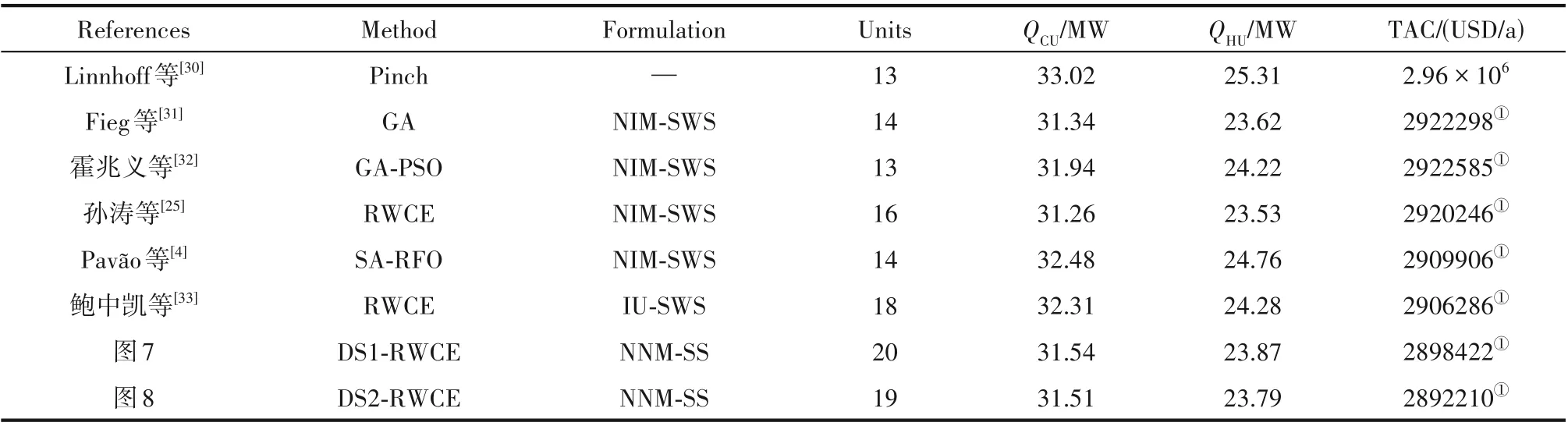
表3 9SP算例优化结果对比Table 3 Comparison of results for 9SP

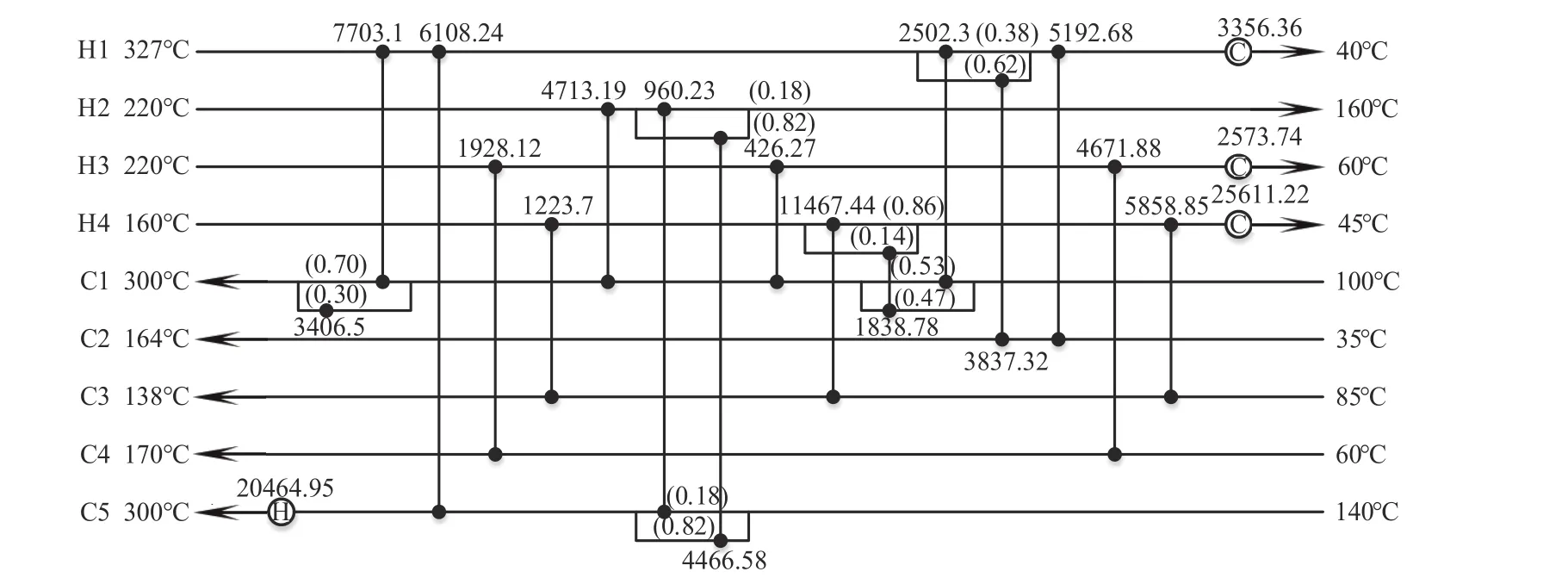
图7 9SP算例RWCE算法优化结果（TAC=2898422 USD/a）Fig.7 Optimization results of RWCE algorithm in 9SP(TAC=2898422 USD/a)

图8 分阶段延缓策略优化9SP最优结果（TAC=2892210 USD/a）Fig.8 9SP optimal results of phased delay strategy optimization（TAC=2892210 USD/a）

表2 9SP在不同优化阶段延缓概率的取值Table 2 Value of delay probability（η）of 9SP in different optimization stages

4.2 算例2

算例2为20SP算例，由10条冷流股和10条热流股组成，换热器费用为8000+800A0.8USD/a，热公用工程费用为70 USD/(kW·a)，冷公用工程费用为10 USD/(kW·a)，该算例当前最优结果是由Rathjens等[22]将连续空间局部优化策略应用到遗传算法中得到的1715088 USD/a。初始节点参数设置为ndH=ndC=6，nfH=nfC=2，mdH=mdC=1，采用RWCE 算法得到如图9 的网络结构，年综合费用为1721621 USD/a；将延缓策略应用到RWCE 算法，各策略的延缓参数设置见表4，采用分阶段延缓策略最终优化得到的结构费用为1714524 USD/a，最优结构如图10 所示，与文献中最优结果对比如表5所示。

图9 20SP算例RWCE算法优化结果(TAC=1721621 USD/a)Fig.9 Optimization results of RWCE algorithm in 20SP（TAC=1721621 USD/a）

表5 20SP算例优化结果对比Table 5 Comparison of results for 20SP

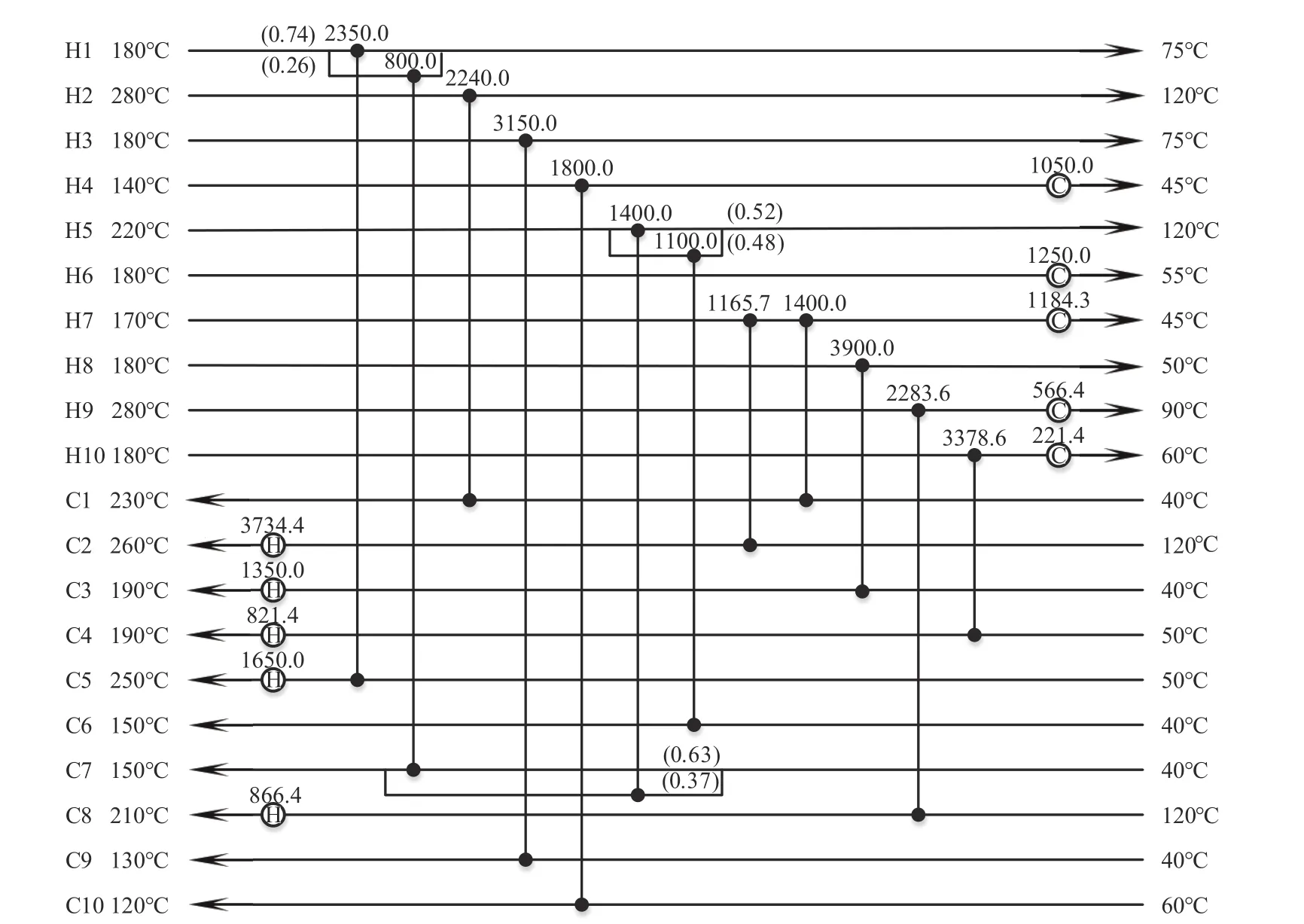
图10 分阶段延缓策略优化20SP最优结果(TAC=1714524 USD/a)Fig.10 20SP optimal results of phased delay strategy optimization（TAC=1714524 USD/a)

表4 20SP在不同优化阶段延缓概率的取值Table 4 Value of delay probability（η）of 20SP in different optimization stages

从结构的对比可发现，加入延缓策略优化后的换热器数量为12 个，其中在H1 流股上生成了分流结构，使得该流股上的匹配方式发生了变化；在C7流股上生成了分流结构，促使与其连接的热流股上的热负荷发生了变化，从而消去了该流股上的热公用工程；H8 上的分流结构被消去了，使换热更为充分，由于换热单元间的耦合关系，C1 流股上的公用工程也被消掉。此外，在延缓策略对结构优化的促进作用下，多个换热器的连接方式发生了变化，网络中分流结构的位置也发生了变化，推动了网络中整型变量的变化，实现了有效跳出局部极值的目的，从而提高了算法的全局搜索能力，获得了更优质的结构。

4.3 算例3

基于上述研究与分析，算例3 采用16SP 算例验证策略的有效性，其中包含6条热流股、10条冷流股。该算例应用广泛，Huo 等[34]结合GA 和PSO 算法优化换热网络得到了7361190 USD/a的有分流优化结果；Rathjens 等[22]采用改进的遗传算法得到了6657080 USD/a的优化结果，为当前文献最优。该算例的特点是H3、H4 和H5 流股受限于进出口温度难以与冷流体形成匹配，仅通过冷公用工程冷却。而H2流股具有较高的温差，更易形成换热匹配。应用分阶段延缓策略优化换热网络，延缓概率在不同优化阶段分别取0.4、0.15、0，得到的优化结果为6651937USD/a，最优结构如图11所示，优化结果与文献中最优结果对比如表6所示，相比文献[22]下降了5143 USD/a，再次验证了阻尼优化方法的有效性。

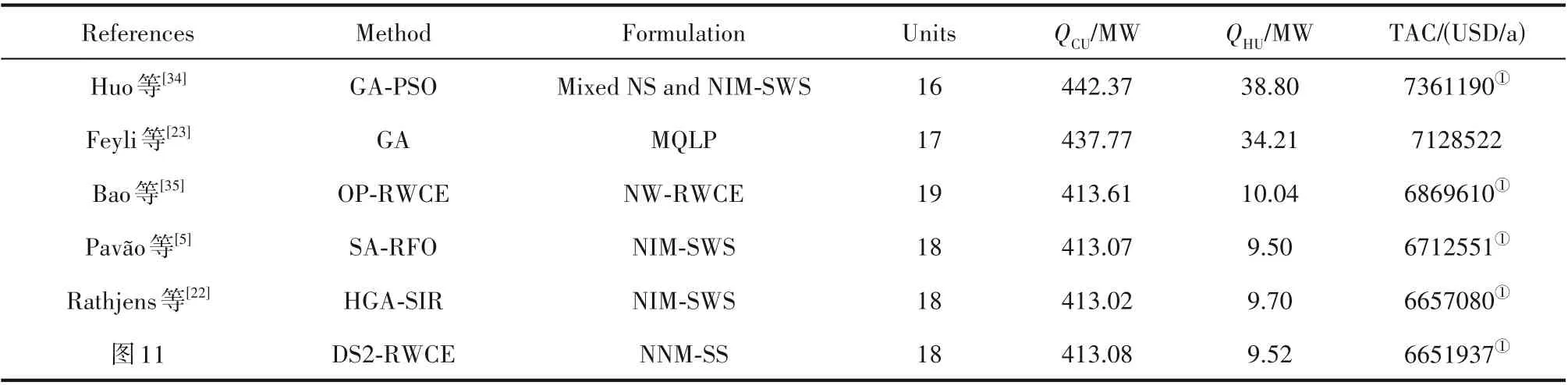
表6 16SP算例优化结果对比Table 6 Comparison of results for 16SP

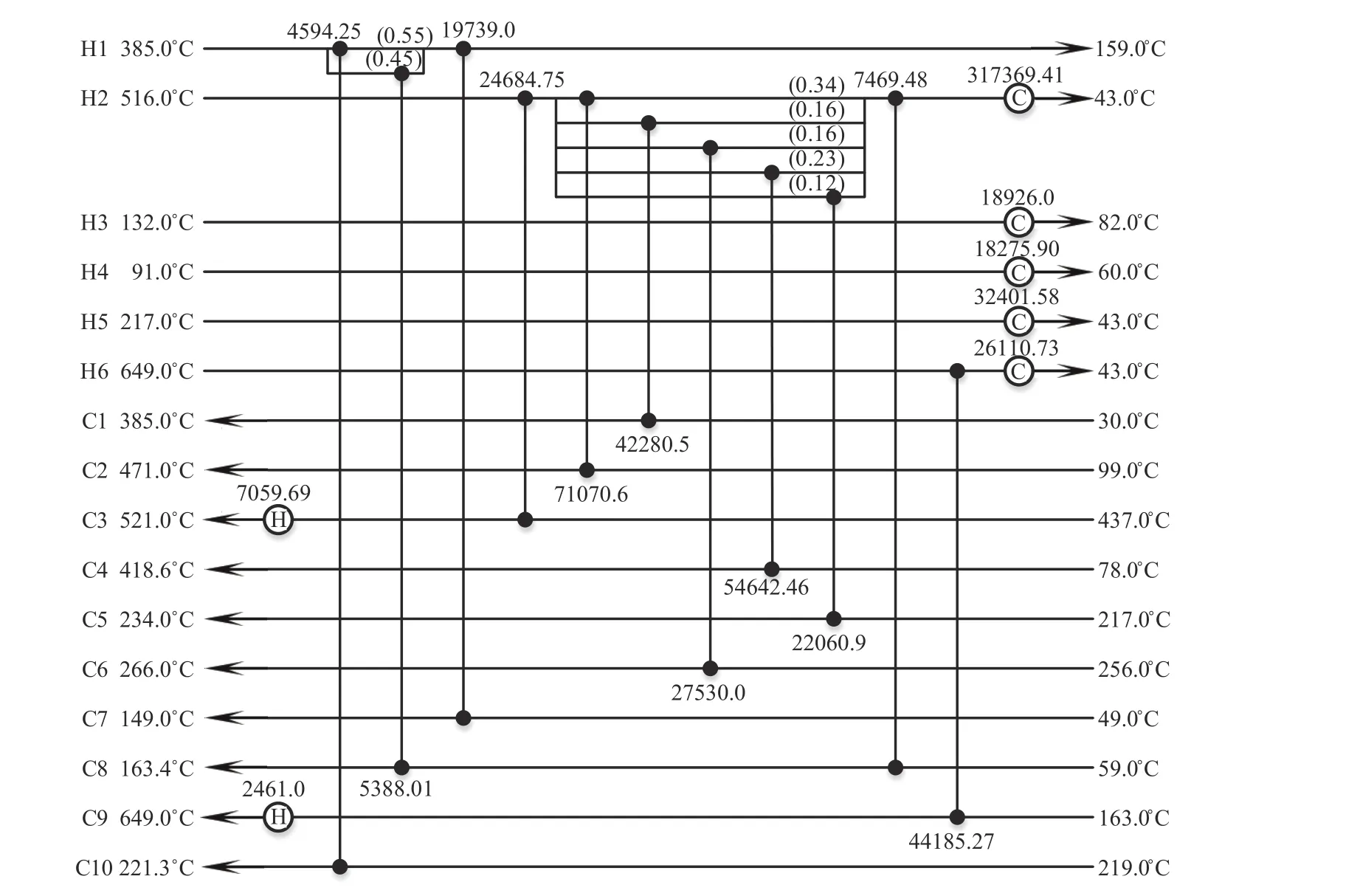
图11 分阶段延缓策略优化16SP最优结果（TAC=6651937 USD/a）Fig.11 16SP optimal results of phased delay strategy optimization（TAC=6651937 USD/a）

4.4 算例4

为进一步论证阻尼方法在优化换热网络问题时的普适性，算例4 采用39SP 算例验证改进策略在优化大规模网络问题上的性能。该算例包含22 条冷流股和17 条热流股，冷、热流股间可形成换热匹配的数量更多，网络结构的复杂性也导致在求解域中存在较多局部极值点。Zhang 等[36]提出将温差均匀性因子的概念引入换热网络，用改进的Powell 粒子群优化算法优化得到的结果为1939149 USD/a；Pavão 等[17]在SA 算法基础上提出的火箭烟花算法得到了1900614 USD/a 的优化结果。在不同优化阶段延缓概率分别取0.4、0.15、0，采用分阶段延缓方法得到的优化结果为1877898 USD/a，最优结构如图12所示，与文献[17]中最优结果对比TAC降低了22716USD/a，且得到了最少的换热单元数目，与文献中原始最优结果对比如表7所示。

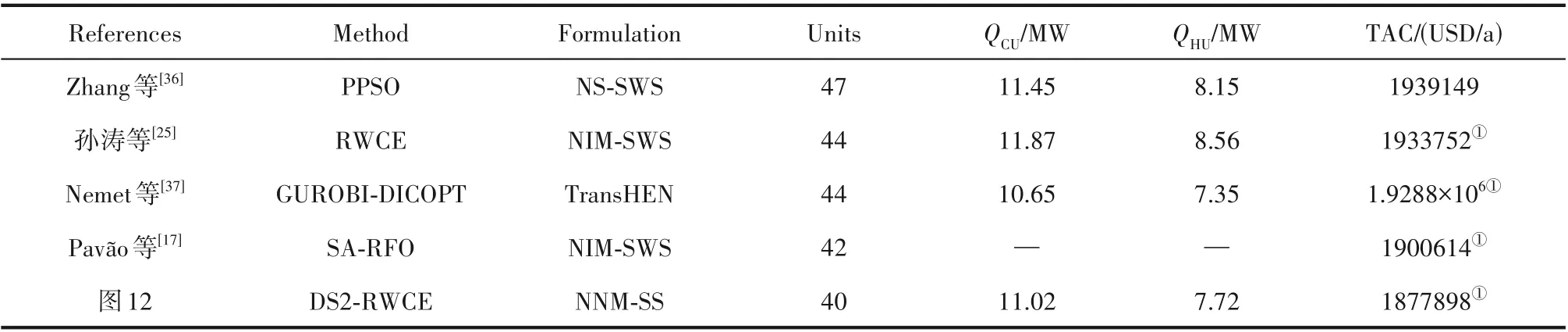
表7 39SP算例优化结果对比Table 7 Comparison of results for 39SP

图12 分阶段延缓策略优化39SP最优结果（TAC=1877898 USD/a）Fig.12 39SP optimal results of phased delay strategy optimization(TAC=1877898 USD/a)

5 结 论

（1）为解决RWCE 算法优化有分流换热网络较早形成固化结构的问题，提出阻尼RWCE 算法，基于延缓形成固化结构的思想提出了两种延缓方式，首先是使用相同延缓概率的全程延缓策略，在此基础上进一步提出了不同优化阶段延缓概率不同的分阶段延缓策略，通过调控在不同优化时期的延缓概率，可促进结构进一步优化从而获得更低的年综合费用。

（2）将延缓策略应用到RWCE 算法时，延缓概率表示接受好解的程度，其取值大小影响改进算法的优化性能，研究分析加入延缓策略在足够的优化时间内对固化结构的形成具有一定的延缓效果，并且能取得更低的优化结果。针对分阶段延缓策略，通过调控在不同优化时期的延缓概率，促进结构变异从而获得更低的年综合费用。

（3）采用9SP、20SP、16SP、39SP 算例验证延缓策 略，分 别 得 到2892210 USD/a、1714524 USD/a、6651937 USD/a、1877898 USD/a 的优化结果，均低于已有文献结果，表明阻尼RWCE 算法在足够的优化时间内对固化结构的形成具有一定的延缓效果，验证了本方法的可靠性。

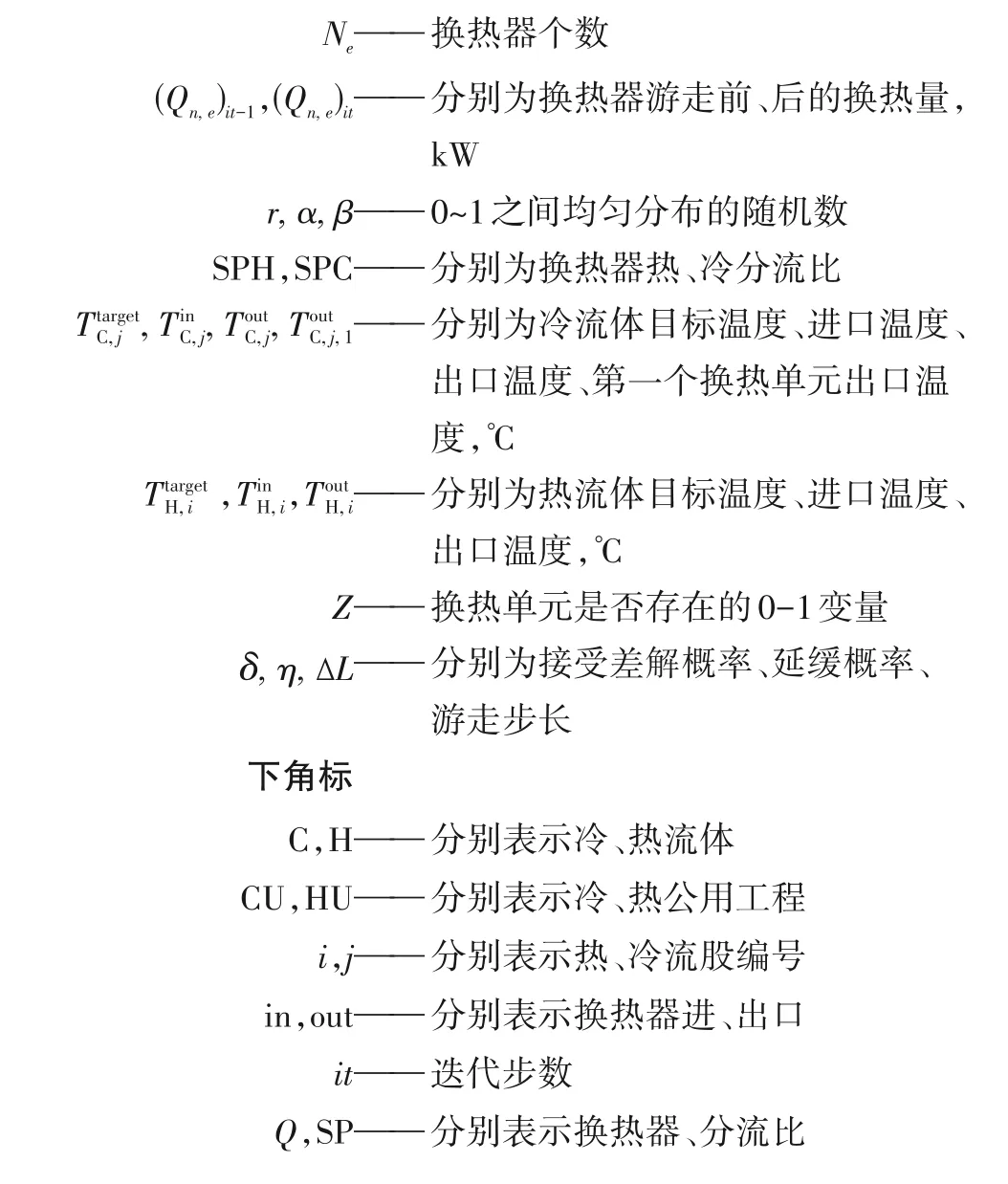
符 号 说 明