卧式单轴捏合反应器流动与混合特性的数值模拟

成文凯，张先明，王嘉骏，冯连芳

（1 浙江理工大学材料科学与工程学院，纺织纤维材料与加工技术国家地方联合工程实验室，浙江杭州 310018；2 浙江大学化学工程与生物工程学院，化学工程联合国家重点实验室，浙江杭州 310027）

引 言

聚合物材料制备过程往往涉及变黏、高黏以及黏弹性等复杂流变特性。因此，从流场结构化和强化混合、传质以及传热等方面着手研发自清洁搅拌设备，开发高效率、低能耗、短流程的聚合与脱挥工艺，对于促进聚合工业的发展至关重要[1-5]。瑞士List 公司开发了新型高效的卧式单轴捏合反应器[6-12]，搅拌槽表面上存在一定结构和数目的钩子，这些钩子和搅拌桨之间会发生捏合作用，具有大的反应空间、优异的混合性能、传热性能、表面更新性能和自清洁性能，已经在本体聚合和聚合物脱挥等领域展现了巨大的优势[13-16]。但是，国内关于这种搅拌设备及其相关的聚合工艺鲜有研究。

Dittler 等[17]通过实验测量和模拟方法研究了一种List卧式单轴自清洁搅拌设备的间歇真空干燥过程。刘荣[18]通过计算流体力学(computational fluid dynamics,CFD)模拟研究了新型卧式单轴自清洁搅拌设备的流场特性、搅拌功率特性、停留时间分布特性以及传热与温度分布特性。单纯[19]利用CFD模拟研究了卧式单轴自清洁搅拌釜的流场特性、搅拌功率特性以及停留时间分布特性，搅拌桨的旋转运动采用滑移网格技术进行模拟。研究表明，搅拌釜内的流场无明显死角，物料黏度对搅拌功率的影响较大，这种搅拌釜不适用于低黏度流体的搅拌混合。罗彬彬[20]采用CFD模拟研究了卧式单轴自清洁搅拌釜中重力对气液分层流场的影响和高黏度流体在搅拌釜内的传热过程，搅拌桨的旋转运动采用动网格技术。结果发现，重力对于低黏度和高黏度流体的气液分层的流场具有显著影响，转速对平均对流传热系数的影响最大。然而，关于卧式单轴捏合反应器流动与混合过程的研究尚未见报道。有限元（finite element method, FEM）数值模拟在研究复杂搅拌设备中的流动与混合过程等方面具有很好的优势[21-30]。

因此，本文通过三维有限元数值模拟方法研究了高黏度牛顿流体糖浆在卧式单轴捏合反应器的流动过程，利用粒子示踪技术来分析反应器的全局与局部分布混合过程，对示踪粒子的运动轨迹进行统计分析得到了拉伸率与混合效率，并且探讨了搅拌结构对流动与混合过程的影响，期望研究结果可以为卧式单轴捏合反应器的设计提供一定的理论基础和指导思路。

1 三维有限元数值模拟

1.1 卧式单轴捏合反应器的几何构型

设计了两种结构的卧式单轴捏合反应器（single-shaft kneader, SK）来研究其流动与混合特性，分别定义为SK1[图1(a)]和SK2[图1(b)]。搅拌槽的直径和长度分别为140 和300 mm。搅拌轴和搅拌桨叶的直径分别为40 和130 mm。每个搅拌桨叶由4 个捏合杆组成，相邻两个捏合杆的相位角为90°。SK1 中仅安装了4 个搅拌桨叶，相邻两个搅拌桨叶之间的中心距为60 mm。SK2 的搅拌轴上安装了4 个搅拌桨叶，其结构与尺寸与SK1 相同。SK2的搅拌槽壁面上安装了6 个反向的静态捏合杆（static kneading bar），分别放置在搅拌轴水平中心截面两侧，其形状与尺寸和搅拌轴上的动态捏合杆（dynamic kneading bar）相同。捏合杆的长度为45 mm，侧边长度为25 mm。SK2 中的动态捏合杆与静态捏合杆的初始相位角为0°。

图1 卧式单轴捏合反应器示意图Fig.1 Schematic sketch of two types of horizontal single-shaft kneaders

1.2 控制方程

高黏糖浆在卧式单轴捏合反应器中的流动可以近似为不可压缩的等温层流流动。

连续性方程为：

式中，v为速度矢量，m/s。

动量守恒方程为：

式中，T,p,ρ,t,f分别为额外应力张量，压力（Pa），流体密度（kg/m3），时间（s），体积力（N）。

采用网格叠加技术（mesh superposition technique，MST）来模拟卧式单轴捏合反应器的搅拌运动。在一定的时间间隔内分别对流道和搅拌桨叶划分网格，然后将这两部分网格进行组合[28-30]。流道和搅拌桨叶有部分网格重合，在数值模拟过程中通过坐标变换来判定流道网格、搅拌桨叶网格以及两者共有的网格。因此，动量守恒方程变为如下形式：

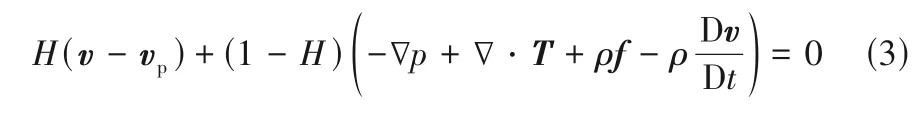
网格叠加技术使用了惩罚项H(v-vp)[30]。其中，H是阶跃函数。当网格点为流体域时，H=0；当网格点为搅拌结构时，H=1。此处的速度为搅拌结构的转速，vp为搅拌结构的速度（m/s）。

1.3 计算网格与网格无关性验证

为了减小计算量，选取卧式单轴捏合反应器的部分结构进行模拟计算，其计算域如图1（b）所示。采用Gambit 2.3 软件分别对SK1 和SK2 进行网格划分，流道边缘部分采用边界层加密，得到的六面体结构化网格如图2所示。图2（a）、（b）分别为SK1和SK2 搅拌桨叶的计算网格示意图，图2（c）为SK1 和SK2流道的计算网格示意图。

对SK2划分不同数目网格以进行网格无关性验证，网格数目分别为164022，282294 和438582。在SK2中选取一条平行于搅拌轴的直线来分析网格数目对流速的影响，如图2（d）所示。该直线两个点的坐标分别为（0.055 m, 0 m, 0 m）和（0.055 m, 0 m,0.14 m）。结果表明，当网格数目大于282294 时，流速几乎不随着网格数目的增加而改变。因此，数值模拟中SK1 和SK2 的网格数目分别为267294 和282294。

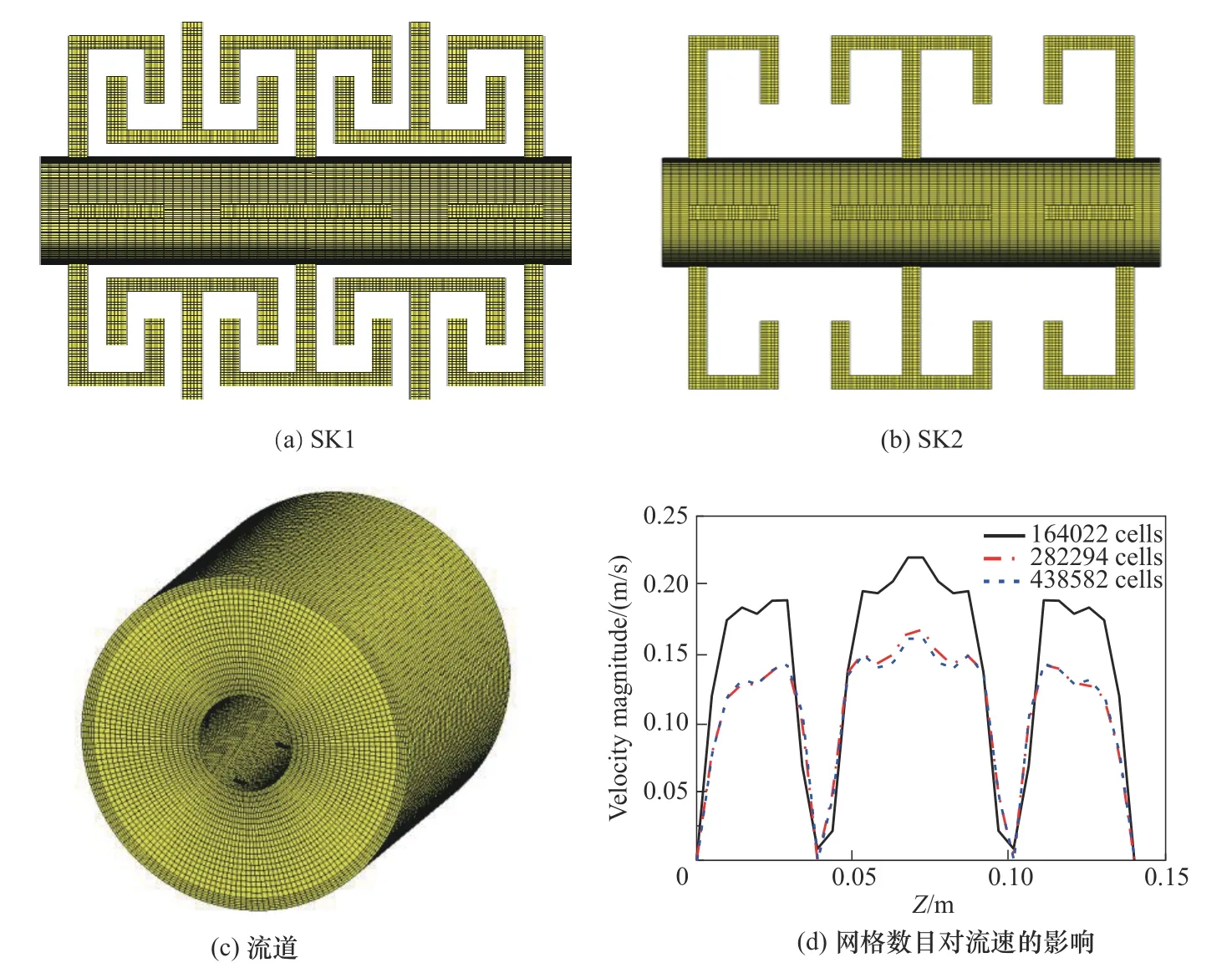
图2 计算网格与网格无关性验证Fig.2 Computational grid and grid independence verification

1.4 边界条件与模拟策略

选取牛顿流体高黏糖浆为研究物料，其黏度和密度分别为68 Pa·s 和1472 kg/m3。通过计算流体力学Polyflow 3.10.2 软件来模拟高黏糖浆在卧式单轴捏合反应器中的间歇等温层流流动过程，考虑重力和惯性。反应器壁面和搅拌桨叶表面均采用无滑移边界条件。选用网格重叠技术来模拟搅拌桨叶的复杂运动过程。采用非稳态模拟，时间步长为0.0625 s。搅拌转速为30 r/min。

1.5 混合过程表征

采用粒子示踪技术剖析捏合反应器中的混合过程，假设如下：（1）忽略粒子的质量以及粒子之间的相互作用；（2）示踪粒子不影响反应器中的流场，其运动过程只依赖于速度场。

Eulerian速度场为：

示踪粒子的运动轨迹可由式（5）求得：

当t=0 s 时，x=x(x0,y0,z0)。在局部坐标中，采用4 阶显式Runge-Kutta 程序，从t=0 s 开始，在很短的时间间隔内对式（5）进行积分来确定粒子的新位置，接着以该位置为起点求解示踪粒子的新位置，重复上述步骤直至相应的计算要求。

Danckwerts[31]提出分离尺度Ls（m）来定量表征混合器中的混合过程，其表达式为：

分离尺度表示分离区域的平均尺寸。在t时刻，对于M对材料点，分开距离为r的两个点浓度的相关系数可由式（7）求得：

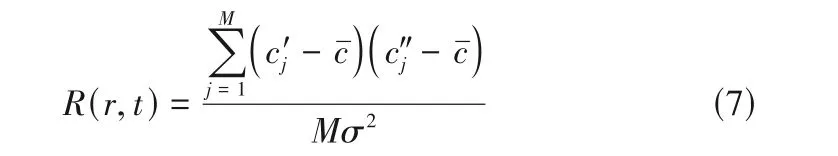
式中，c′j，c″j分别为第j对粒子点的浓度；cˉ为所有粒子点的平均浓度；σ为标准方差，其表达式为：

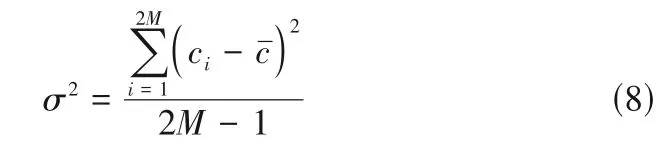
相关系数R(r,t)的取值范围为[-1,1]。当R(r,t)为1 时，表示距离为r两个粒子的浓度相同（两个粒子点为纯的连续相或者分散相）。当R(r,t)为-1 时，表示距离为r两个粒子的浓度完全相反（一个粒子点为纯的连续相，另一个粒子点为纯的分散相）[29-30]。

Yang 等[32]提出离散两两相关函数来定量表征反应器的分布混合程度。对于N个粒子的混合系统，粒子对的数目为N(N-1)/2。可利用粒子点之间的距离变化来分析分布混合，其两两相关函数为：

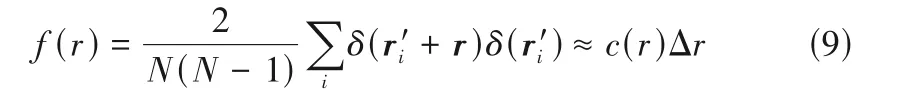
式中，f(r)为粒子之间距离为r± Δr/2相关函数的系数；δ(r)为一个delta函数，其值为1或0（当有一个粒子出现在半径为r± Δr/2 的球壳中，其值为1；当没有粒子出现在半径为r± Δr/2 的球壳中，其值为0）。因此，f(r)也可以表示为粒子对之间距离在r± Δr/2范围内的概率：

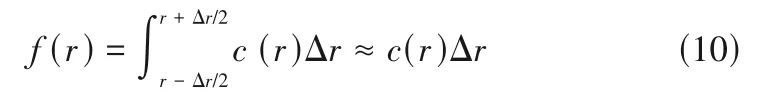
式中，c(r)为概率分布函数的系数。曲线c(r)不依赖于分布的形状，其积分面积为定值：

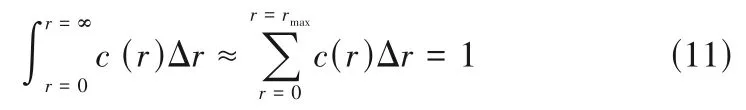
式中，rmax为混合系统的最大尺寸。当粒子对之间的距离r＞rmax时，c(r) =0。但该函数不能比较不同尺寸反应器的混合性能，因而利用两两相关函数指数来表征真实分布和理想分布之间的差异，其表达式为：

式中，ε为在给定的时间下，一簇粒子的真实概率分布函数系数与理想最优随机分布系数标准偏差。Connelly 等[29-30]将该函数叫作粒子簇分布指数。ε的取值范围为0～1，值为1表示所有粒子的位置相同，值为0表示粒子为最优随机的理想分布。ε非常依赖于粒子数目和起始位置，与流动区域的尺寸大小无关。

Ottino[33]提出一种动力学方法来定量表征混合器的分布混合性能，这种方法是通过追踪流体单元在混合器中的运动过程中线、面或体变形进行统计分析。在流动区域中，单位取向M的线段，在时间t后变为单位取向为m的线段dx=F· dX。其中，F为形变梯度。

拉伸率为：

对数拉伸率为：

平均对数拉伸率为：

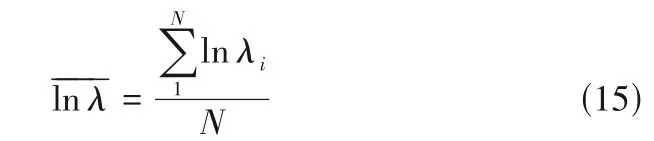
式中，N为示踪粒子的数目。

瞬时混合效率eλ定量地表征了混合过程中的拉伸速率[29-30]，其取值范围为[-1,1]。eλ为1 表示所有耗散的能量都用于拉伸材料线，eλ为-1 表示所有耗散的能量都用于缩短材料线的长度，其表达式为：

式中，D为应变速率张量，是速度梯度张量的对称部分。

平均瞬时混合效率为：

时均混合效率为：

平均时均混合效率为：

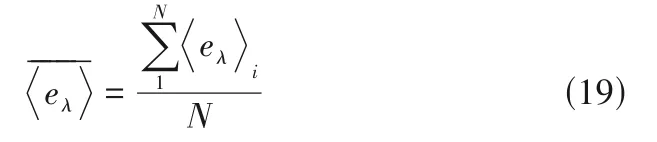
对于分散混合过程，拉伸流比剪切流更为有效。Cheng 等[34]提出了混合指数（λMZ）来分析反应器中的流场，进而评价其分散混合性能。λMZ的取值范围为0～1，当λMZ=0 时，流场为旋转流；当λMZ=0.5时，流场为剪切流；当λMZ=1 时，流场为拉伸流。当使用λMZ来评价反应器中的分散混合时，通常需要考虑其对应的剪切应力大小。

混合指数定义为：

式中，Ω为涡量张量，是速度张量的非对称部分。

2 混合实验装置与方法

搭建了卧式单轴捏合反应器SK1[图3(a)]和SK2[图3(b)]的可视化实验装置来研究其分布混合过程。SK1 搅拌槽的材质为透明的聚甲基丙烯酸甲酯，SK2 搅拌槽的材质为不锈钢，搅拌轴和搅拌桨的材质为不锈钢。搅拌槽的长、高和宽分别为300、140和140 mm。搅拌轴和搅拌桨的直径分别为40 和130 mm。在SK1 搅拌槽中放置四个搅拌桨，相邻两个桨叶的中心距为60 mm。每个搅拌桨仅由四个捏合杆组成，相邻两个捏合杆的夹角为90°。在SK2搅拌槽中安装4 个搅拌桨，其结构与尺寸和SK1 相同，SK2搅拌槽壁面上安装6个静态捏合杆，在搅拌槽上下两个区域均布，静态捏合杆的结构和尺寸与动态捏合杆相同。选用高黏糖浆为实验物料（湖北德安府糖业有限责任公司），其黏度为68 Pa·s，密度为1472 kg/m3。糖浆溶液的黏度采用旋转流变仪NDJ-8S（上海力成科技有限公司）进行测量。选用红色的红曲米（上海佳杰天然食品色素有限公司）和绿色的菠菜粉（康美来天然食品有限公司）为示踪剂。红曲米的密度和粒径约为0.94 g/ml 和11.12 μm，菠菜粉的密度和粒径约为1.45 g/ml和10.03 μm。

图3 SK1和SK2的可视化实验装置Fig.3 Visual experimental device for SK1 and SK2

3 结果与讨论

3.1 模型验证

图4、图5 分别为SK1 和SK2 间歇混合实验与CFD 模拟对比图。将混有红曲米与菠菜粉的糖浆分别放置于SK1 和SK2 的左右两侧区域，其轴向混合如图4(a)和图5(a)所示。将混有红曲米与菠菜粉的糖浆分别放置于SK1 和SK2 的上下两侧区域，其径向混合如图4(c)和图5(c)所示。数值模拟中，将红色与蓝色示踪粒子分别放置于SK1和SK2的不同区域来模拟其混合过程，图4(b)和图5(b)分别为SK1和SK2 的轴向混合CFD 模拟图，图4(d)和图5(d)分别为SK1 和SK2 的径向混合CFD 模拟图。结果表明，SK1 和SK2 中分布混合过程实验结果与CFD 模拟数据吻合较好，且搅拌釜的径向混合过程优于轴向混合过程。从图4(a)、(b)，图5(a)、(b)中可以看出，两种不同颜色的界面几乎不随着混合过程的进行而发生改变，因而在间歇混合过程中SK1 和SK2 几乎没有轴向推动力，可以通过改变搅拌桨的倾斜角来改善其轴向输送能力。从图4(c)和图5(c)中可以看出，随着混合过程的进行，搅拌釜上方区域的红色物料运动到下方区域，绿色物料在搅拌釜表面的面积越来越小。从图4(d)和图5(d)中可以看出，随着混合过程的进行，搅拌釜上方区域的红色粒子运动到下方区域，搅拌釜下方区域的蓝色粒子运动到上方区域。

图4 SK1的混合过程实验与CFD模拟对比图Fig.4 Mixing process comparison between experiment and CFD simulation for SK1

图5 SK2的混合过程实验与CFD模拟对比图Fig.5 Mixing process comparison between experiment and CFD simulation for SK2

3.2 流速分布

在SK2 中选取了Z=0.055 m 平面（图1）来分析其流型演变过程，如图6 所示。可以发现，搅拌釜中几乎没有流动死区，搅拌桨末端的流速最大。当t=0.5 s 时，搅拌轴上的动态捏合杆与流道上的静态捏合杆相互重叠。当t=0.625 s 时，桨叶以顺时针方向进行旋转，动态捏合杆与静态捏合杆相互背离。当t=1 s 时，动态捏合杆与静态捏合杆相互重叠。可见，搅拌轴上的动态捏合杆与流道上的静态捏合杆之间存在周期性的捏合作用[15]，其捏合周期与捏合杆的数目以及搅拌转速有关。

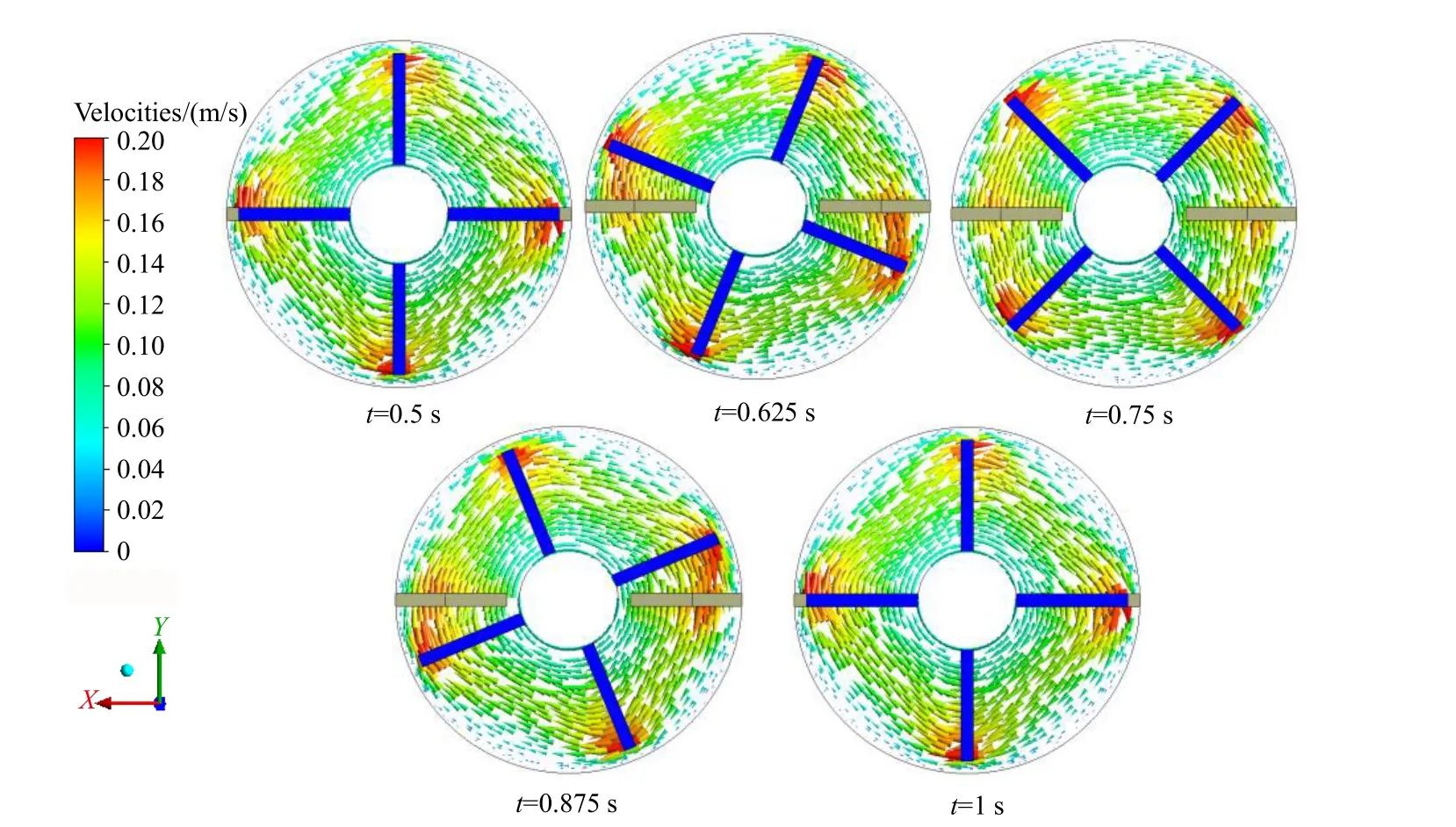
图6 SK2中Z=0.055 m平面上速度矢量图随时间的变化Fig.6 Evolution of velocity vectors on plane Z=0.055 m in SK2

图7 为不同平面的速度分布云图。可以看出，SK2中搅拌槽边缘区域的高流速区域大于SK1，SK2中靠近搅拌轴区域的低流速区域大于SK1，这是由于SK2流道上存在静态捏合杆。从图6、图7中还可以看出，SK2中存在捏合作用，因而具备一定的自清洁性能[15]。

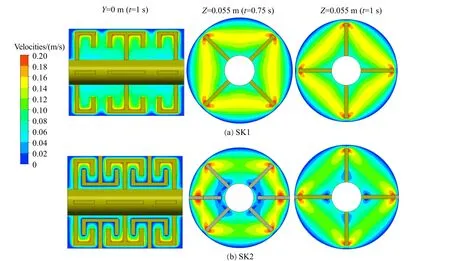
图7 不同平面上速度分布云图Fig.7 Contours of velocity magnitude on different planes

3.3 分布混合

SK1和SK2的轴向分布混合过程分别如图8（a）、（b）所示。在捏合反应器中随机放置5000 个材料点，左侧（-0.07 m＜x＜0.07 m;-0.07 m＜y＜0.07 m;0 m＜z＜0.07 m）红色材料点的浓度为1，右侧（-0.07 m＜x＜0.07 m; -0.07 m＜y＜0.07 m; 0.07 m＜z＜0.14 m）蓝色材料点的浓度为0。可以看出，两种颜色粒子的界面几乎不随混合过程的进行而发生变化。因此，分离尺度在很小的范围内进行波动，如图8（c）所示。

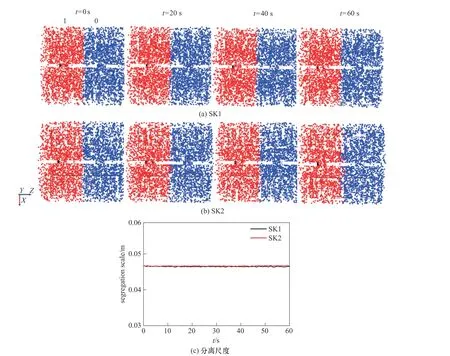
图8 轴向分布混合过程与分离尺度（左侧红色点浓度为1，右侧蓝色点浓度为0）Fig.8 Axial distributive mixing process and segregation scale

SK1 和SK2 的径向分布混合过程分别如图9（a）、（b）所示。在捏合反应器中随机放置5000个材料点，左侧（0 m＜x＜0.07 m; -0.07 m＜y＜0.07 m;0 m＜z＜0.14 m）红色材料点的浓度为1，右侧（-0.07 m＜x＜0 m;-0.07 m＜y＜0.07 m;0 m＜z＜0.14 m）蓝色材料点的浓度为0。SK1 和SK2 中左侧的红色材料点运动到右侧，而右侧的蓝色材料点运动到左侧。随着混合过程的进行，左右两侧均存在红色和蓝色的材料点。当t=6 s 时，SK1 中仅流道边缘处两种颜色示踪粒子的混合较好，搅拌轴附近存在较大的红色和蓝色的粒子团簇，SK2 的混合效果优于SK1。当t=12 s时，SK1 中依旧存在红色和蓝色的粒子团簇，而SK2中几乎没有红色或者蓝色的粒子团簇。可以看出，SK2 的径向分布混合过程比SK1 快速高效。这是由于SK2 的搅拌槽壁面存在静态捏合杆，动态捏合杆与静态捏合杆的间隙很小，具有较大速度梯度和剪切作用，且动态捏合杆与静态捏合杆存在周期性的交互作用。这些因素均有利于打破粒子团簇，将两种颜色的粒子混合起来。

图9（c）为SK1和SK2径向分布混合对应的分离尺度。当t=0 s 时，SK1 和SK2 的分离尺度分别为0.0471 和0.0467 m，两者差异很小。当t=6 s 时，SK1和SK2 的分离尺度分别为0.0089 和0.0072 m，两者比较接近。当t=60 s 时，SK1 和SK2 的分离尺度分别为0.0088 和0.0021 m。可以看出，当混合时间小于6 s 时，SK1 的分离尺度减小的速率快于SK2，这是由于SK2 流道上存在静止的捏合杆，阻挡了材料点的运动过程，进而影响两种颜色材料点的混合过程。当混合时间大于6 s时，SK2 中存在周期性的捏合作用，可以强化径向分布混合过程，因此，SK2 的分离尺度小于SK1。

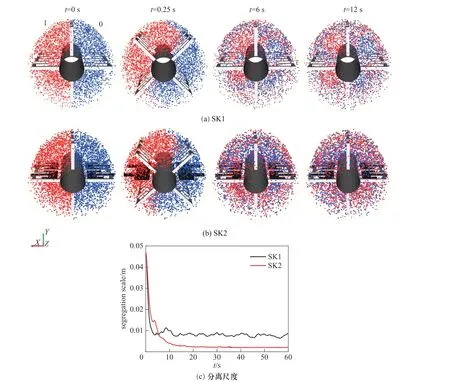
图9 径向分布混合过程与分离尺度（左侧红色点浓度为1，右侧蓝色点浓度为0）Fig.9 Radial distributive mixing process and segregation scale

SK1和SK2的局部分布混合过程如图10(a)、(b)所示。在捏合反应器中左侧放置一个粒子簇，包含3000个材料点，该粒子簇的坐标为（0.025 m＜x＜0.065 m;-0.02 m＜y＜0.02 m; 0.05 m＜z＜0.09 m）。当t=1 s 时，SK1 中的粒子簇发生了较大的形变，且绝大部分材料点从左侧移动到右侧，SK2 流道上存在静态捏合杆，会阻挡材料点的运动，部分材料点从左侧移动到右侧。当t=5 s 时，SK1 和SK2 中的材料点分布到反应器的上部和下部空间，SK2 中的材料点分布情况优于SK1，SK1 绝大部分材料点分布在反应器的边缘区域，靠近搅拌轴区域的材料点较少。随着混合过程的进行，SK1中的材料点依然分布不均匀，靠近搅拌轴部分区域的材料点很少，而SK2 中的材料点分布越来越均匀。

图10（c）为SK1 和SK2 的粒子簇分布指数对比图。可以看出，当混合时间小于5 s 时，SK1 的粒子簇分布指数小于SK2。这是因为SK2 的流道上存在静态捏合杆，会阻挡材料点的运动，进而影响材料点的分布混合。随着混合过程的进行，SK2 中材料点的分布混合优于SK1，SK2 的粒子簇分布指数小于SK1。SK2 中存在周期性的捏合作用，且动态捏合杆与静态捏合杆的间歇小，剪切速率大，因而可以强化局部分布混合过程。

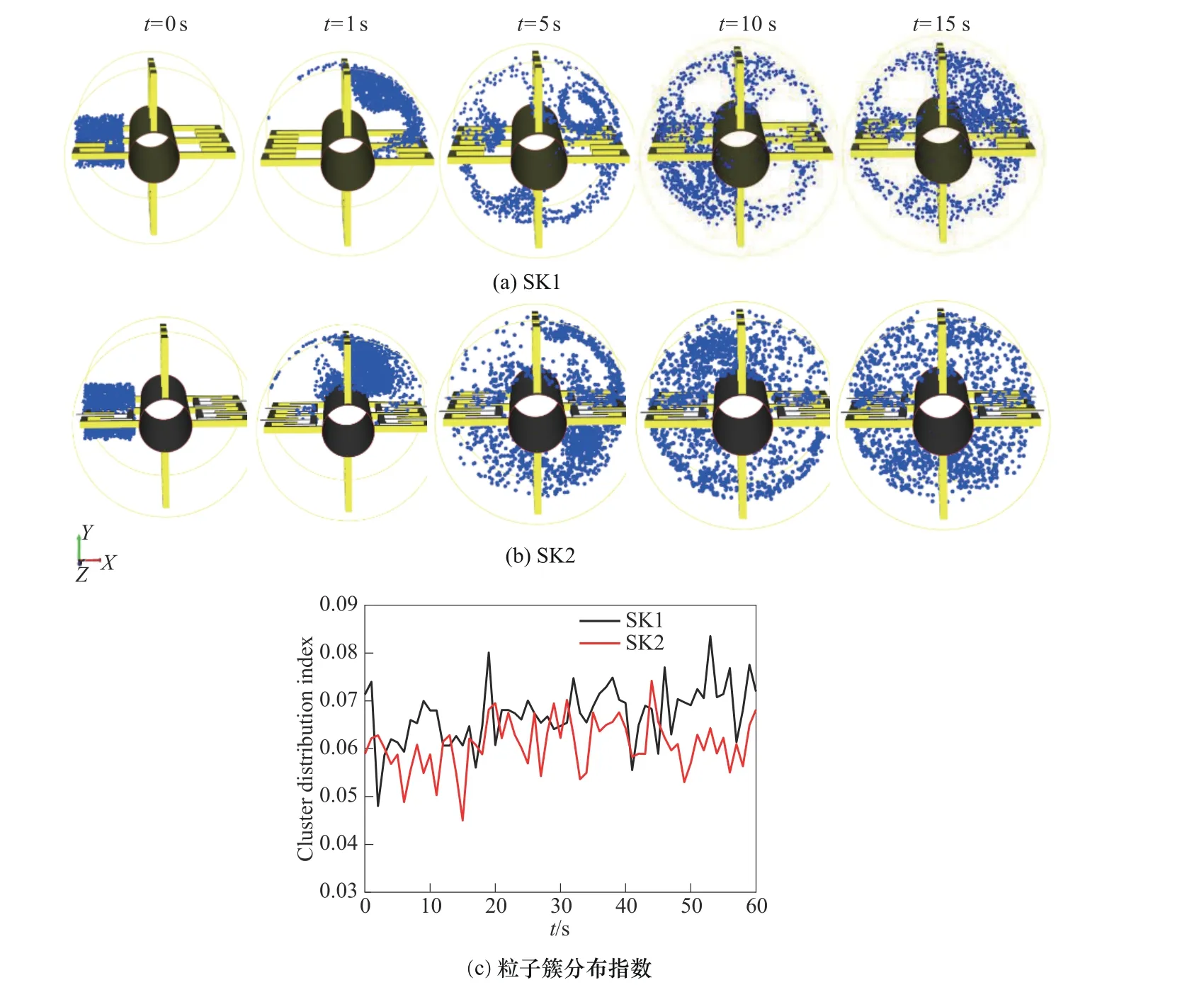
图10 局部分布混合过程与粒子簇分布指数Fig.10 Local distributive mixing process and particle cluster distribution index

3.4 分散混合

图11（a）、（b）分别为SK1 和SK2 中不同平面上局部剪切速率分布云图。可以看出，SK2 的剪切速率大于SK1。SK2 中的动态捏合杆与静态捏合杆之间存在周期性的捏合作用，搅拌釜中会形成小间歇区域，具有很大的速度梯度。图12（a）、（b）分别为SK1 和SK2 中不同平面上混合指数分布云图。SK1和SK2 中的流型主要为剪切流动，SK2 的混合指数大于SK1。当搅拌槽安装静态捏合杆时，高混合指数区域逐渐增大。可以看出，静态捏合杆可以强化搅拌釜的剪切作用以及分散混合性能。因此，SK2的分散混合性能优于SK1。

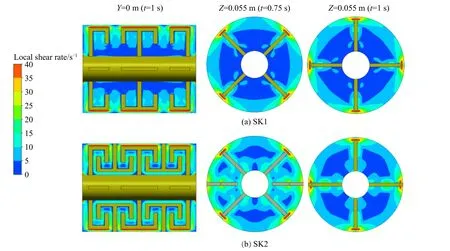
图11 不同平面上剪切速率分布云图Fig.11 Contours of shear rate on different planes

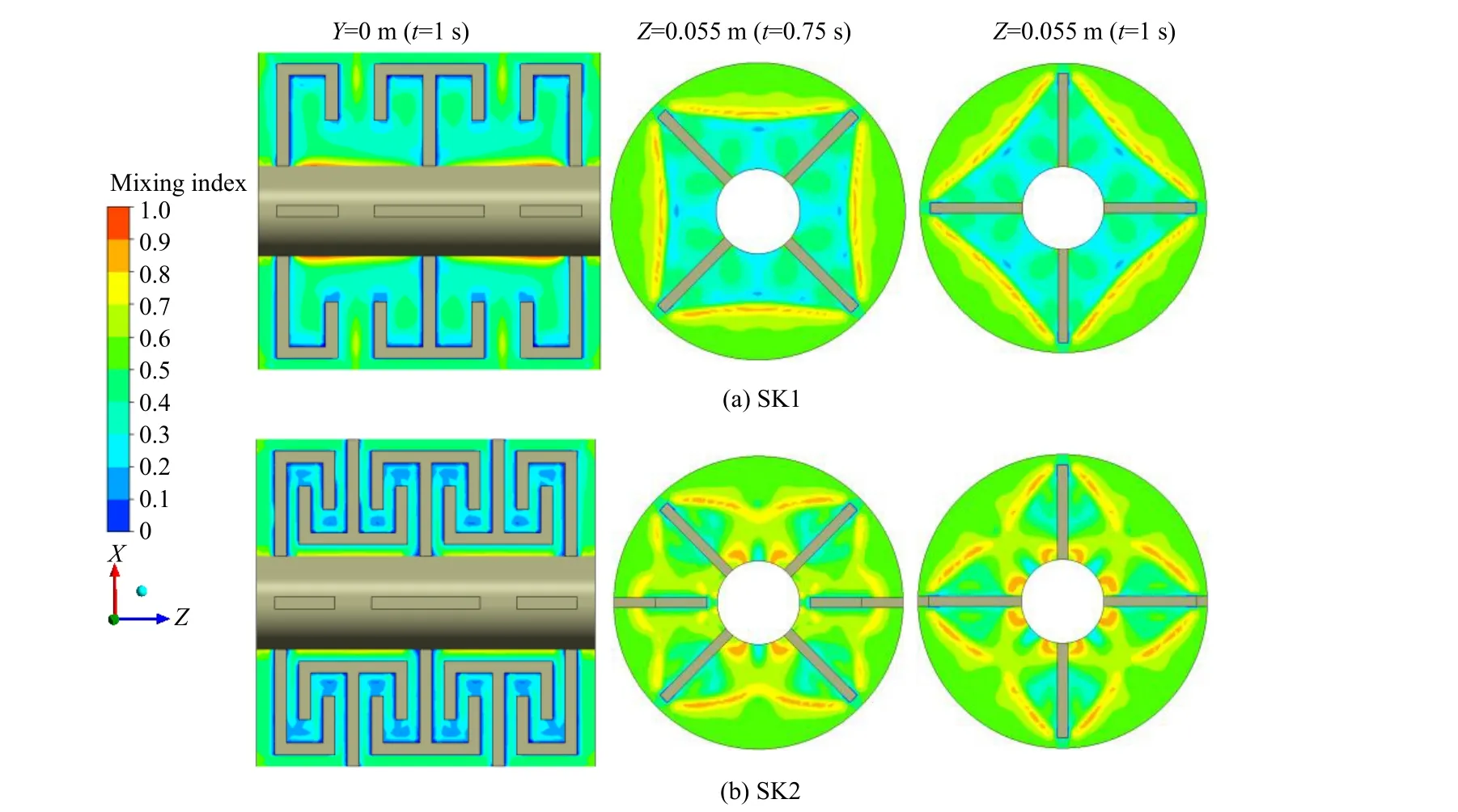
图12 不同平面上混合指数分布云图Fig.12 Contours of mixing index on different planes

3.5 拉伸与混合效率

在SK1和SK2中分别随机放置5000个粒子，通过粒子示踪技术得到粒子运动轨迹，进一步统计分析得到拉伸率与混合效率。图13（a）、（b）分别为SK1 和SK2对数拉伸率随混合时间的变化。可以看出，SK2中的示踪粒子的对数拉伸率随时间增长的幅度快于SK1，且SK2中具有较大拉伸率的示踪粒子分布比较均匀，这说明SK2具有良好的分布混合性能[27]。

图13 对数拉伸率随时间的变化Fig.13 Evolution of natural log of length of stretch with time

图14（a）、（b）分别为平均对数拉伸率和平均时均混合效率随混合时间的变化图。从图14（a）中可以看出，SK1 和SK2 的平均对数拉伸率几乎随着混合时间线性增加。因此，SK1 和SK2 的拉伸率随着混合时间呈现指数形式增加，这是高效层流混合的必要条件[33]。当混合时间小于5 s 时，SK1 和SK2 的平均对数拉伸率差异很小。当混合时间大于5 s时，SK2 的平均混合效率大于SK1，且增长的速率远大于SK1。当混合时间为60 s时，SK1和SK2的平均对数拉伸率分别为8.185和18.237。

从图14（b）中可以看出，当混合时间小于25 s时，SK1 的平均时均混合效率大于SK2。当混合时间大于25 s 时，SK1 的平均时均混合效率小于SK2。当混合时间为60 s 时，SK1 和SK2 的平均时均混合效率分别为0.0345 和0.0463。这是因为在混合初期，SK2 搅拌槽壁面上的静态捏合杆会阻碍示踪粒子的运动，影响其混合过程与混合效率。随着混合时间的增加，SK2 中动态捏合杆与静态捏合杆之间存在周期性的捏合作用，可以强化剪切作用和混合过程。由此可见，SK2 搅拌槽壁面上的静态捏合杆可以强化拉伸作用以及混合效率。

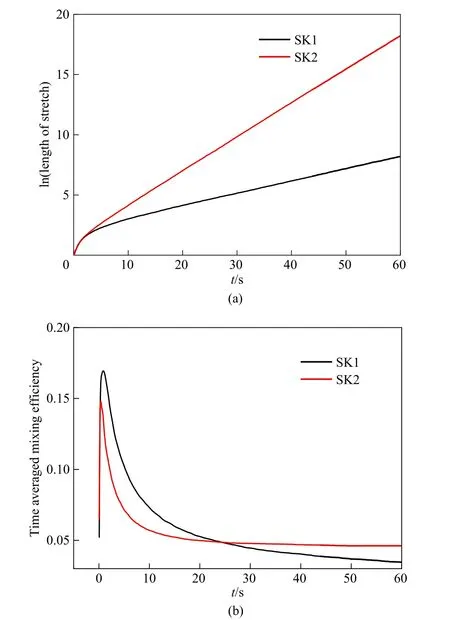
图14 搅拌结构对平均对数拉伸率(a)和时均混合效率(b)的影响Fig.14 Effect of kneader configuration on mean length of stretch(a)and mean time averaged mixing efficiency(b)

4 结 论

（1）卧式单轴捏合反应器中几乎没有流动死区，搅拌桨末端的流速最大，静态捏合杆与搅拌轴之间区域的流速较小。搅拌轴上的动态捏合杆与搅拌槽壁面上的静态捏合杆之间存在周期性的捏合作用，因而具备一定的自清洁性能，也可以强化剪切作用以及分散混合性能。

（2）卧式单轴捏合反应器的径向分布混合过程优于轴向分布混合过程。尽管静态捏合杆在混合过程的初期会在一定程度上限制示踪粒子的运动，但是动态捏合杆与静态捏合杆之间的捏合作用可以快速打破粒子团簇，进而强化整体分布混合过程以及局部分布混合过程。

（3）动态捏合杆与静态捏合杆之间的捏合作用可以提升拉伸率与混合效率。卧式单轴捏合反应器的拉伸率随着混合过程的进行呈现指数形式增加，时均混合效率大于零，这表明卧式单轴捏合反应器具备良好的层流混合性能。