三角槽道低Reynolds 数脉动流与柔性壁耦合特性研究

黄其，章晓敏，宓霄凌，周楷，钟英杰

（1 浙江高晟光热发电技术研究院有限公司，浙江湖州 313000； 2 浙江工业大学能源与动力工程研究所，浙江杭州 310000）

引 言

脉动流作为一种扰流技术，已得到了广泛的关注与研究，成为流体力学领域的重点分支之一。大量的研究表明：相比稳态流，脉动流具备强化传热特性，尤其是在周期性凹槽流道中[1-6]；在低Reynolds数条件下，脉动流也表现出增强流体掺混、阻挠污垢形成、解决流体分配不均等显著效果。但是，脉动流带来诸多益处的同时，也相应出现了一系列的问题，例如流态复杂化、流阻增加，尤其是在微小流道的设备中[7-9]。因此，在应用脉动流技术时，采用合理的减阻手段解决阻力大幅增加问题，成为当今的主流研究课题之一。

目前，对于流动减阻技术的研究主要分为主动控制和被动控制，具体如图1[10]所示。由于主动减阻技术需要附加设备，会增加系统的复杂性，这就一定程度限制了其应用范围。而被动减阻技术，只要对流体中添加减阻剂或者对壁面采用一定的处理方式[11-15]，就可实现流动减阻，因此，在现有设备的升级改造过程中，采用被动减阻技术，更具应用优势。其中，本文重点关注“柔性壁减阻”技术，主要原因在于：脉动流本身是一种波动流态，从仿生学来说，类似血液流动与波状流，自然界中血管壁及鱼类皮肤均属于柔性表面，故将柔性壁面减阻技术应用到脉动流研究中将非常契合[16-17]。

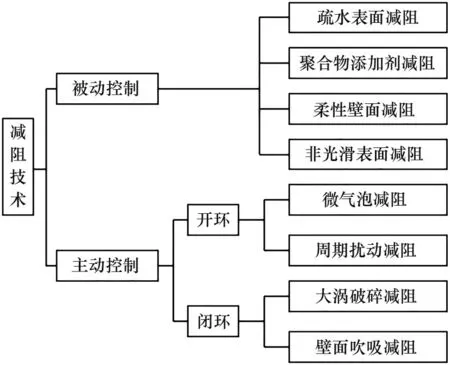
图1 流动减阻技术分类[10]Fig.1 Classification of flow drag reduction techniques[10]

值得注意的是，截至目前，脉动流与柔性壁耦合特性的研究领域相对局限，存在如下不足：（1）脉动流与柔性壁耦合特性研究主要集中于“血液动力学”领域，关注点在于血液流与血管扩缩两者之间的流固耦合关系，得到流动-压降关联性，用于研判病理学问题[18-21]。而工业应用场景（如脉动流换热器、生物反应器）的理论与实验研究严重不足。（2）研究工作主要集中于“湍流减阻”方面[22-23]，对于低Reynolds 数、特殊流态的研究相对较少。（3）针对存有热交换的流体流动过程，缺乏柔性壁减阻与传热效果之间的关联性研究。因此，开展脉动流与柔性壁耦合的传热及流动特性研究将极具工程价值及学术意义。

基于上述原因，本文以具有柔性壁的三角槽道（三角槽道为典型周期性凹槽流道）为研究对象，通过实验测试方式，探究脉动流与柔性壁耦合的传热及流动特性。首先，通过传热与流动实验，分析脉动参数与柔性壁特性对传热及流动的影响；其次，通过可视化实验，解析柔性壁与脉动流的响应关系，阐述柔性壁形变与振频对脉动流传热及流动的作用机制及分离贡献。

1 实验装置及方法介绍

1.1 实验系统

如图2所示，实验系统主要包括测试段（即实验装置）、水循环系统以及数据采集系统三部分。实验系统运行流程如下：

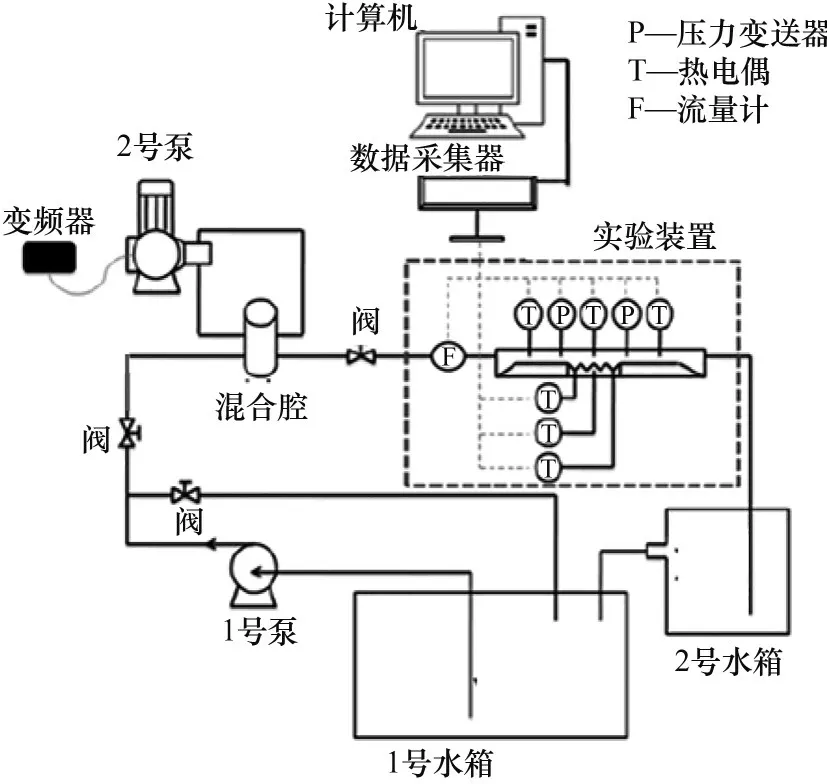
图2 实验系统示意图Fig.2 Schematic diagram of test system

（1）在离心泵（1 号泵）作用下，1 号水箱中的水被抽吸入系统管路；

（2）通过球阀的调节，控制系统中水的流量，多余部分水回流入1号水箱；

（3）管路中的水，进入混合腔，受到隔膜泵（2 号泵）的影响，水流由稳态流转变为脉动流；

（4）脉动流进入测试段，进行传热与流动等多种测试实验；

（5）最终，流经测试段的脉动流，进入2 号水箱。

1.2 实验装置

本次实验对象为三角槽道，如图3所示。其中，三角槽深度（a）为2 mm、长度（L）为4 mm，流道宽度（X）为50 mm，主流通道高度（h）为4 mm。

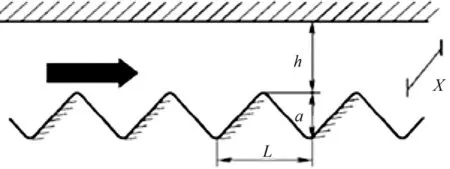
图3 三角槽道示意图Fig.3 Schematic diagram of triangular grooved channel

为形成底面的三角槽，定制了三角槽型热沉底板（图4）嵌入流道中。另外，在做传热实验时，将电加热膜贴于三角槽型热沉底板（图5），对其进行加热，进而与流道中的水进行热交换。电加热膜选用聚酰亚胺薄膜（单条膜片：尺寸为10 mm×110 mm，功率36 W，供电电压24 V）；前述热沉底板的安装详见文献[24]。

图4 热沉底板Fig.4 Heat sink plate

图5 敷设的电加热膜Fig.5 Electrical heating

另外，为保证测试段的压力与温度等参数的测试准确性，对流道结构进行喇叭口与缓冲区等特殊设计，详见文献[24]。

1.2.1 传热及流动实验 如图6 所示，传热测试的实验装置主要由直流电源、电加热膜、热电偶以及装置本体组成，其中，加热过程采用恒热流模式；阻力测试的实验装置，主要由压力变送器、装置本体组成，其中，通过引压管将压力变送器与三角槽道出入口连通。前述压力变送器与热电偶两者产生的相应信号，均是通过NI-DAQ 多功能数据采集仪进行采集。传热实验过程，采用保温棉对实验装置进行保温处理，以减少由于散热损失带来的测量误差。特别说明：实验装置流道特性（抑或刚性，抑或柔性），均是通过更换上壁板实现。刚性流道采用亚克力板，柔性流道采用硅胶板[柔性流道的传热、流动及可视化实验选用1 mm厚的硅胶板；刚度变化通过调整硅胶板壁厚（0.5～3 mm）实现]，如图7所示。

图6 实验装置Fig.6 Experimental device

图7 上壁板材料Fig.7 Upper panel material

1.2.2 可视化实验 如图8 所示，可视化实验装置主要由CCD 相机、标尺以及装置本体组成。其中，为便于拍摄柔性壁的变形情况，将上壁板的压紧电木板更换为0.5 mm厚的刚性压板。

图8 可视化实验装置Fig.8 Experimental device for displacement test

图9 给出了实验状态下通水与未通水时的图片，通过对比可以发现，图9（b）中压板上方出现了较为明显的鼓起部分，定义该部分变形高度为柔性壁变形高度。为便于观察柔性壁变形情况，下文将呈现观察区的局部放大图。

图9 实验拍摄图Fig.9 Image of experiment

1.3 实验可靠性验证

在进行正式的测试实验之前，将实验段变更为矩形通道（刚性壁条件），进行稳态层流流动实验，获得相应的换热量、流阻系数与Reynolds数关系图，用以校对实验系统。其中，流阻系数理论值根据文献[25]的公式计算得到。由图10 可知，实验值与理论值吻合度较高，表明实验系统相对可靠，具备进行传热与流动实验条件。

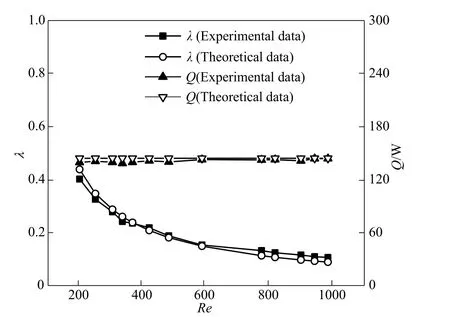
图10 实验系统验证Fig.10 Validation of experimental system

1.4 实验参数

实验介质为水，实验系统的主要控制参数设置为：（1）Reynolds 数（Re），控制在200～1000；（2）脉动频率（f），控制在0～5 Hz；（3）脉动振幅（A），控制在平均流速的±50%以内。

另外，传热实验时，采用恒热流的加热模式，加热功率为4×36 W。

1.5 数据处理

入口流速（u）定义式为：

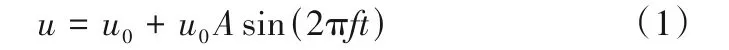
式中，u0为平均流速。

时均Reynolds数（Re）定义式为：

式中，De为等效水力直径；ν为运动黏度。其中，本文的De取值均为h=4 mm时的等效水力直径。

脉动振幅（A）定义式为：

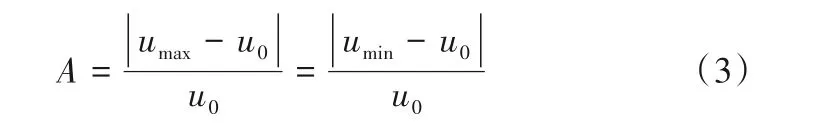
式中，umax与umin分别为瞬时入口流速的峰值与谷值。

W（Womersley 数）表征无量纲脉动频率，定义式为：

对流传热系数（h0）定义式为：

式中，ΔT为壁面与流体之间的温差；Qh为换热量。

强化传热因子（E）定义式为：

式中，h0,p为脉动流条件的时均h0；h0,s为稳态流条件的时均h0。为实现比较对象的一致性，本文中的h0,s均为刚性流道条件。下角标p 代表脉动流，s代表稳态流。

流阻系数（λ）定义式为：

式中，Δp*为压差时均值；l为两个测压点之间的距离；ρ为水的密度。

阻力因子（Eλ）定义式为：

式中，λp为脉动流的流阻系数；λs为稳态流的流阻系数。为实现比较对象的一致性，本文中的λs为刚性流道条件。

材料刚度（Kb）定义式为[26-27]：

式中，e为材料的弹性模量；δ为材料的厚度；I为矩形截面的惯性矩；w为矩形截面的宽度。

2 传热及流动实验结果及讨论

2.1 流道特性对传热及流动的影响

图11 给出了强化传热因子（E）随着脉动频率（W）、脉动振幅（A）的变化。由图11 可知，ER,p＞1.5＞EF,p＞1（下角标R代表刚性流道，F代表柔性流道），表明：（1）脉动流具备强化传热能力且不受流道特性（无论是刚性还是柔性）的影响；（2）相比于柔性流道，脉动流在刚性流道中发挥的强化传热效果更为显著。

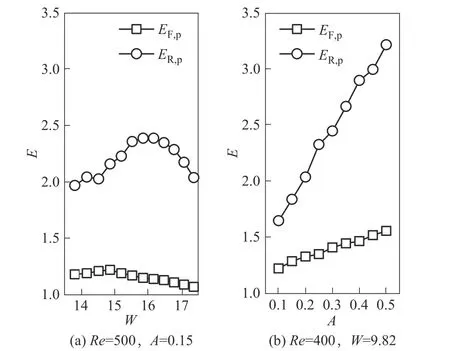
图11 强化传热因子（E）随着脉动频率（W）、脉动振幅（A）的变化Fig.11 Variations of E with W and A

图12 给出了阻力因子（Eλ）随着脉动频率（W）、脉动振幅（A）的变化。由图12 可知，Eλ,R＞1、Eλ,F＜1，表明：相比于刚性流道稳态流，脉动流在刚性流道中将增加阻力而在柔性流道中则并不会造成阻力增加。值得注意的是，随着W与A的增大，Eλ,F进一步减小，柔性流道减阻效果得到强化。

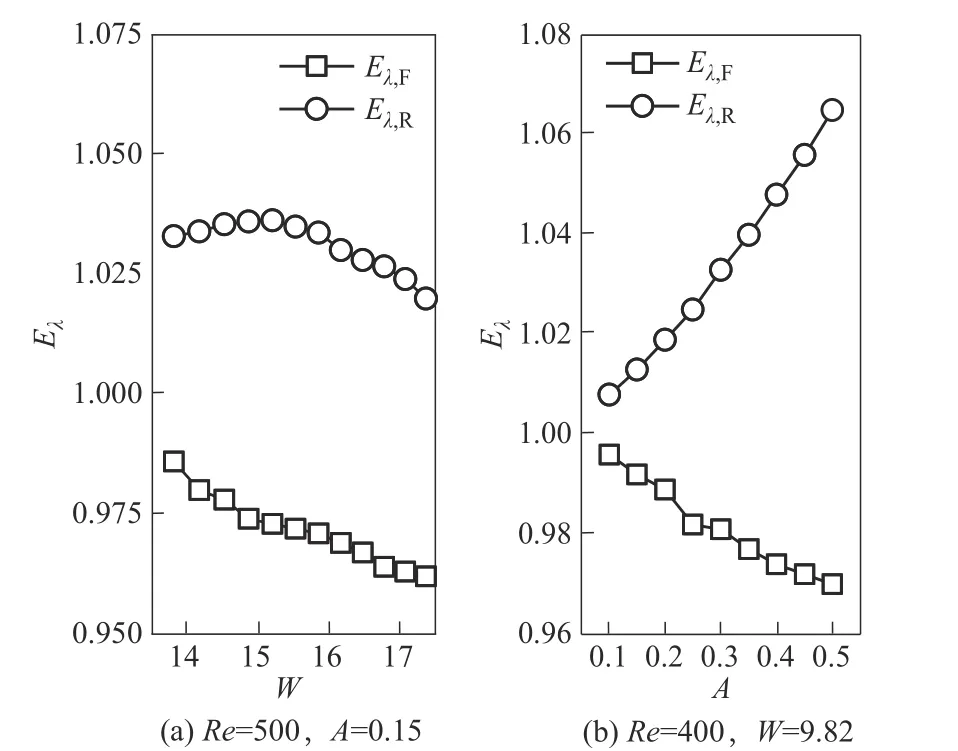
图12 阻力因子（Eλ）随着脉动频率（W）、脉动振幅（A）的变化Fig.12 Variations of Eλ with W and A

图13给出了不同流道特性下强化传热因子（E）与阻力因子（Eλ）的对应关系。通过图13 可以发现：（1）柔性流道条件下，E＞1 且Eλ＜1，表明脉动流与柔性壁耦合可以实现强化传热与流动减阻双重效果。值得注意的是，E的数值较小，起到的强化传热效果相对较弱，但其并不会带来阻力的增加，因此柔性流道脉动流技术更适用于以减阻为主要目的的换热场合。（2）刚性流道条件下，E＞1且Eλ＞1，表明脉动流强化传热的同时伴随着阻力的增加。但是，E的数值较大（最大可达3.0 以上），因此，以强化传热为主要目的，刚性流道脉动流技术更为适用。

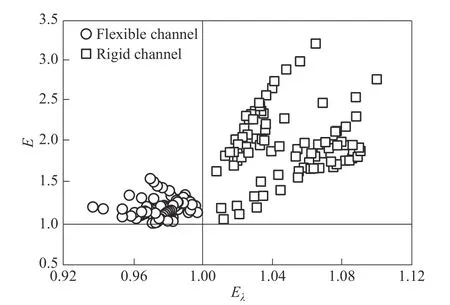
图13 强化传热因子（E）与阻力因子（Eλ）的对应关系Fig.13 Corresponding relations between E and Eλ

2.2 柔性壁刚度对传热及流动的影响

图14给出了强化传热因子（E）与阻力因子（Eλ）随着刚度（Kb）的变化。通过图14 可以发现，E与Eλ均随着Kb增大而增大，这是因为，Kb增大意味着柔性壁变形能力减弱，逐渐趋近于刚性，那么随之就产生了传热性能增强而减阻效果减弱的现象。从物理本质来看，柔性壁变形能力减弱，将严重影响脉动流与柔性壁的动态响应，故而造成柔性壁无法有效遏制脉动能量，导致湍流度提高[28-30]。

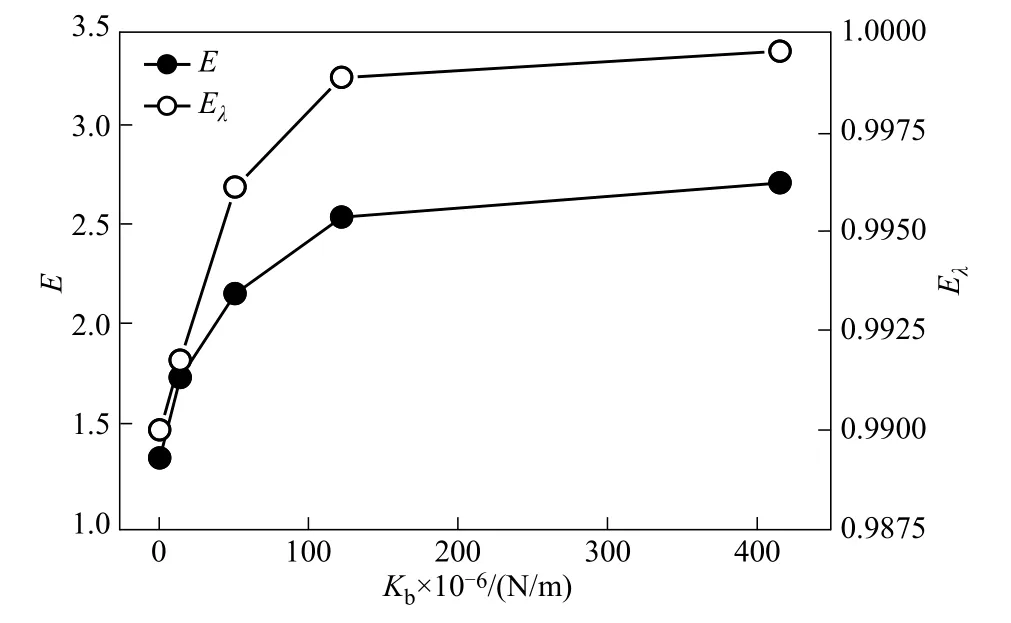
图14 强化传热因子（E）与阻力因子（Eλ）随着刚度（Kb）的变化（Re=500，W=9.82，A=0.15）Fig.14 Variations of E and Eλwith Kb（Re=500,W=9.82,A=0.15）

3 可视化实验结果及讨论

上文呈现了脉动流在柔性流道中传热与流动特性，同时文献[28-30]也表明了柔性壁与脉动流相互耦合作用机制，为进一步论证柔性壁与脉动流作用关系，深入解析柔性壁受到脉动流影响后的“变形量”与“振频”两者针对传热与流动过程造成的影响程度，将通过可视化实验进行研究。

3.1 柔性壁与脉动流的响应特性

图15 柔性壁位移的峰值与谷值图（Re=400，A=0.4）Fig.15 Image of peak and valley values of flexible wall displacement（Re=400,A=0.4）

图16 给出了在三种振幅下的柔性壁位移峰值与谷值图。通过图16 可以发现：（1）随着A的增大，柔性壁位移峰值递增，而柔性壁位移谷值递减。经测算，时均变形量依次（对应A=0.2、A=0.4、A=0.6）增大，表明流道截面随着A增大而增大，也起到流体降速减阻效果；（2）柔性壁振动幅度随着A的增大而增大，其对流体脉动起到削弱作用，也减少了流体能量消耗。

图16 柔性壁位移的峰值与谷值图（Re=400，W=7.2）Fig.16 Image of peak and valley values of flexible wall displacement（Re=400,W=7.2）

图17 给出了三种刚度条件的柔性壁位移峰值与谷值图。通过图17可以发现，柔性壁位移峰值与谷值，均随着Kb的增大而下降，变形能力逐步减弱，导致柔性壁抑制流体扰动的能力被削弱。这就很好地论证了2.1 节传热实验中所述柔性流道脉动传热效果随着Kb的增大而增大的现象。

图17 柔性壁位移的峰值与谷值图（Re=400，W=7.2，A=0.4）Fig.17 Image of peak and valley values of flexible wall displacement（Re=400,W=7.2,A=0.4）

3.2 柔性壁的时均变形量与振频对传热的分离贡献

脉动传热的准则方程，拟合式为[31]：

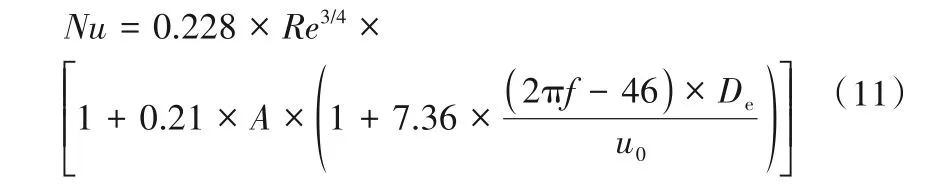
对流传热系数（hc）定义式为：

式中，k为流体的热导率。

传热削减的柔性壁变形占比（M1），定义式为：

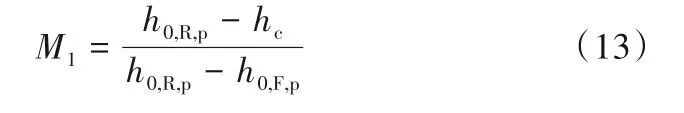
式中，hc为基于拟合式（12）计算所得的对流传热系数（水力直径按柔性流道的时均变形量换算）。

二是夯实基础，着力构建科学合理、操作性强的考核指标体系。明确纳污红线管理所需考核、评估指标，以及相应的总体和阶段控制目标，使纳污红线管理的依据更充分，标准更明确。

传热削减的振动占比（M2）定义式为：

根据图11（a），无论是刚性流道还是柔性流道，脉动流均具备强化传热效果，但是，在脉动流条件下，相比刚性流道，柔性流道对强化传热效果会进行削减。因此，为进一步明确柔性壁的强化传热效率削减是由变形、振频造成的影响占比，给出了传热削减的柔性壁变形占比（M1）与振频占比（M2）随着脉动频率（W）、脉动振幅（A）的变化趋势，如图18、图19所示。

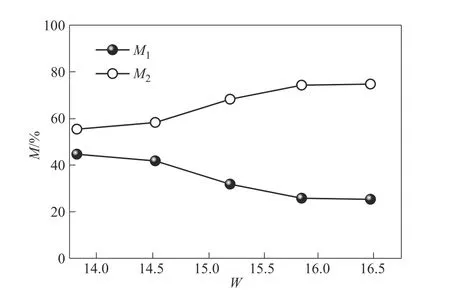
图18 传热削减的柔性壁变形占比（M1）与振频占比（M2）随着脉动频率（W）的变化（Re=400，A=0.4）Fig.18 Variations of M1 and M2 with W（Re=400,A=0.4）

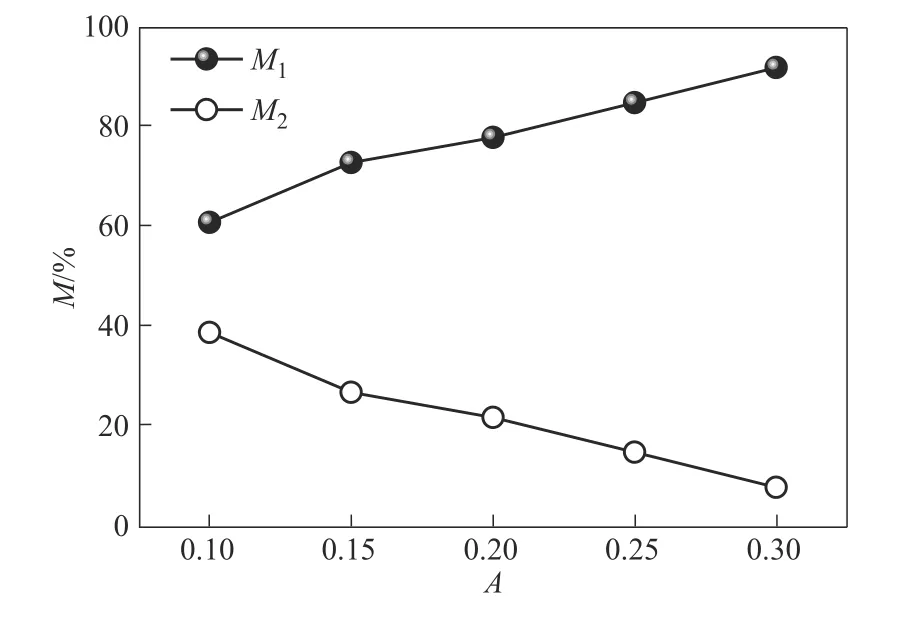
图19 传热削减的柔性壁变形占比（M1）与振频占比（M2）随着脉动振幅（A）的变化（Re=400，W=7.2）Fig.19 Variations of M1 and M2 with A（Re=400,W=7.2）

通过图18、图19 可以发现：（1）随着W的增加，M2呈现上升趋势而M1则相应下降，表明脉动频率的增加将使得柔性壁振频对脉动流强化传热效率的削减逐步趋于主导地位。（2）随着A的增加，M1呈现上升趋势而M2则相应下降，表明脉动振幅的增加将使得柔性壁变形对脉动流强化传热效率的削减逐步趋于主导地位。

3.3 柔性壁的时均变形量与振频对流动的分离贡献

阻力削减的柔性壁变形占比（D1）定义式为：

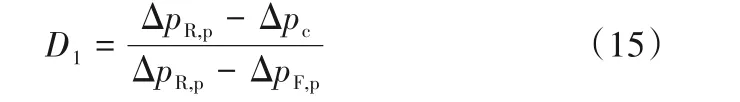
式中，Δpc为泊肃叶方程[式（7）]计算所得的压降（水力直径按柔性流道时均变形量换算）；ΔpR,p与ΔpF,p均为实测值。

阻力削减的振动占比（D2）定义式为：

图12 呈现出，相比刚性流道稳态流，脉动流在刚性流道将增加阻力而在柔性流道中则表现出阻力下降现象。为论证脉动流条件下柔性壁变形与振频对阻力削减的影响，给出了阻力削减的柔性壁变形占比（D1）与振频占比（D2）随着脉动频率（W）、脉动振幅（A）的变化，如图20、图21所示。

通过图20、图21 可以发现：（1）随着W、A的增加，D1与D2的变化较为平缓，数值保持相对稳定。也就是说，柔性壁变形与振频对阻力的削减作用受到脉动参数的影响相对较小，几乎可以忽略。（2）D1均超过70%，表明脉动流阻力的削减主要来自于柔性壁的变形，而柔性壁振频对于脉动流能量耗散的抑制作用较为次要。

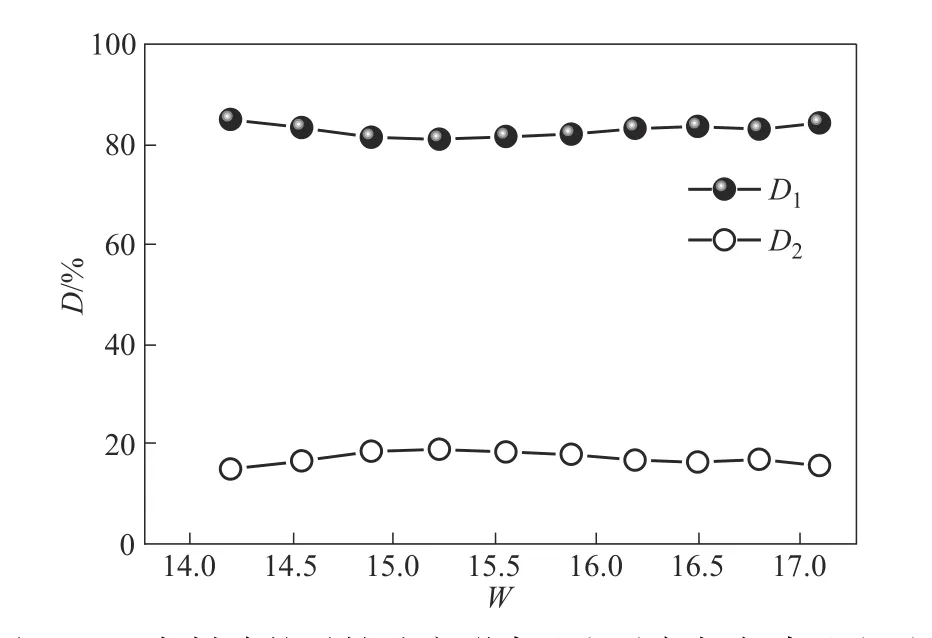
图20 阻力削减的柔性壁变形占比（D1）与振频占比（D2）随着脉动频率（W）的变化（Re=400，A=0.4）Fig.20 Variations of D1 and D2 with W（Re=400,A=0.4）

图21 阻力削减的柔性壁变形占比（D1）与振频占比（D2）随着脉动振幅（A）的变化（Re=400，W=7.2）Fig.21 Variations of D1 and D2 with A（Re=400,W=7.2）

4 结 论

（1）脉动流具备强化传热能力且不受流道特性（无论是刚性还是柔性）的影响，且在刚性流道中发挥的强化传热效果更为显著。

（2）脉动流技术的应用选择：①柔性流道脉动流可以实现强化传热与流动减阻双重效果，但强化传热效果相对较弱（传热效率提升0～50%），因此柔性流道脉动流技术更适用于以减阻为主要目的的换热场合；②刚性流道脉动流强化传热的同时伴随着阻力的增加，但其最大传热效率提升可达200%以上，因此以强化传热为主要目的，刚性流道脉动流技术更为适用。

（3）从可视化实验来看，随着W与A的增大，柔性流道脉动流减阻率提高而强化传热效率下降，主要原因在于：①随着W与A的增大，流道截面时均流通面积增大，造成流体时均流速下降，扰流程度减弱；②随着W与A的增大，柔性壁振频加剧且变形幅度增大，有利于阻碍大尺度涡旋破碎且抑制近壁区小尺度涡旋产生，脉动能量与扰流能力将下降。另外，随着Kb的增加，柔性壁变形能力减弱，逐渐趋近于刚性壁特性，故而造成强化传热因子与阻力因子增加。

（4）柔性壁变形与振频对强化传热效率削减的分离贡献：①随着W的增加，M2上升而M1下降，表明脉动频率的增加将使得柔性壁振频对脉动流强化传热效率的削减作用逐步趋于主导地位；②随着A的增加，M1上升而M2下降，表明脉动振幅的增加将使得柔性壁变形对脉动流强化传热效果的削减作用逐步趋于主导地位。

（5）柔性壁变形与振频对阻力削减的分离贡献：①柔性壁变形与振频对阻力的削减作用受到脉动参数的影响相对较小，几乎可以忽略；②D1均超过70%，表明脉动流阻力的削减主要来自于柔性壁的变形，而柔性壁振频对于脉动流能量耗散的抑制作用较为次要。

符 号 说 明

A——脉动振幅，%

a——三角槽深度，mm

De——等效水力直径，m

D1，D2——分别表示阻力削减的柔性壁变形占比和阻力削减的振动占比，%

E——强化传热因子

Eλ——阻力因子

e——材料的弹性模量，Pa

h——主流通道高度，mm

I——矩形截面的惯性矩，m4

Kb——材料刚度，N/m

k——热导率，W/(m·K)

L——三角槽长度，mm

l——两个测压点之间的距离，m

M1，M2——分别表示传热削减的柔性壁变形占比和传热削减的振动占比，%

Δp*——压差时均值，Pa

Qh——换热量，J

ΔT——壁面与流体之间的温差，℃

u——入口流速，m/s

umax，umin——分别为瞬时入口流速的峰值与谷值，m/s

u0——平均流速，m/s

W——Womersley 数

w——矩形截面的宽度

X——流道宽度，mm

δ——材料的厚度，m

λ——流阻系数

ν——运动黏度，Pa·s

ρ——水的密度，kg/m3