辐射系统热响应特性研究

赵 靖，王佩佩，李佳玉，吕宇凌

（天津大学 环境科学与工程学院 建筑环境与能源天津市重点实验室，天津 300072）

0 引言

辐射式系统因相比于对流式具有更高的热舒适性而被广泛使用［1］，但辐射式系统与室内空气传热存在大延迟效应，传统运行调控中往往没有充分考虑这一系统的热响应特性，导致系统供能与建筑实际负荷需求在时间序列上不匹配，室内热环境不达标，并造成较高能源消耗的问题。可见，研究辐射式系统的热响应特性对系统的精确调控具有重要意义。

国内外很多学者进行了辐射式系统的传热特性相关研究［2］。薛红香等［3］探讨了散热器、风机盘管、地板辐射、毛细管辐射4种室内供暖末端设备的特点，发现地板辐射传热所需的稳定时间长，毛细管辐射所需的稳定时间处于散热器和地板辐射之间。LI等［4］通过试验分析了毛细管辐射吊顶的动态性能及其对室内温度的影响，结果表明，系统开启后室内温度随毛细管进水温度的升高而升高，滞后时间约30 min。由于辐射式系统的传热过程复杂，因此影响其传热特性的因素较多。高志宏等［5］发现辐射板的传热主要受系统特性和供水温度的影响。JEONG等［6］建立了金属辐射冷却板估算模型，通过估算影响冷却板制冷能力的因素，得到各影响因素与制冷能力的简化回归模型。但目前关于辐射式系统延迟效应的具体分析和延迟时间的计算方法研究较少，因此本文基于辐射式系统传热的延迟效应，提出一种计算开启阶段建筑热响应时间的方法，用来指导系统的开启时间，这对于提高负荷供需在时间序列上的匹配程度，降低系统的运行能耗具有重要的研究价值。

1 理论与方法

1.1 热响应时间定义

辐射式传热由于系统热惯性大，向室内传热存在延迟效应，但目前的研究对于这一热响应特性所需的时间描述并不统一，本文将前后2个时间步之间的温度变化小于0.2 ℃的情况称为温度达到稳定状态，根据各稳定时间的含义做统一定义。

系统响应时间：从系统开启至辐射表面温度稳定所需要的时间，如式（1）所示，反映了系统介质的流动延迟与辐射板内部的传热特性。

式中 ts——系统响应时间，min；

t1——辐射表面温度稳定时刻；

t0——系统开启时刻。

末端传热延迟时间：从辐射表面温度稳定至室内温度稳定所需要的时间，如式（2）所示，反映了辐射系统末端的传热特性与建筑围护结构热惰性的综合作用。

式中 td——末端传热延迟时间，min；

t2——室内温度稳定时刻。

开启阶段建筑热响应时间：上述2个时间之和，如式（3）所示，代表从设备开启至室内温度初次达到稳定状态所需要的时间，反映了辐射式系统与建筑围护结构热惯性的综合作用。

式中 tor——开启阶段建筑热响应时间，min。

1.2 研究方法

本研究通过试验测试的方法，测量室内空气温度、内表面温度、供回水温度等参数，得到系统响应时间。再根据实测数据建立毛细管辐射末端传热的CFD模型，进行不同供回水平均温度和初始室内温度工况下末端传热延迟时间的研究。最后利用SPSS软件进行回归分析得到开启阶段建筑热响应时间的计算模型。该方法可为相关工程在运行调控中计算系统开启时间提供指导，其研究流程如图1所示。

图1 开启阶段建筑热响应时间计算流程Fig.1 Flow chart for calculating the building thermal response time in the opening phase

2 试验测试

系统响应时间与管长、管径以及换热介质流速有关，由于案例建筑的毛细管系统管径小、换热介质流速低几乎恒定，属于层流流动［7］，故确定该系统响应时间为一定值。可通过试验测试得到的实验小室室内空气温度、内表面温度以及毛细管供回水温度等数据，观察系统供回水温度的变化得到该案例建筑的系统响应时间，并将测试结果作为数值模拟计算建模和验证的基础。

2.1 试验测试系统

测试对象为天津市某办公建筑的毛细管辐射系统，末端由管间距20 mm、厚度0.5 mm的U型PPR毛细管网组成，直接裸露安装。该系统通过辐射板表面、室内表面和室内空气之间的辐射和自然对流来控制室内热环境，根据室内温度传感器，通过调节管道上电动双通阀的开关来控制系统，减少室内温度波动。为了避免太阳辐射和室内人员的干扰，在建筑内选取合适的公共区域，搭建实验室空间，如图2所示，实验小室空间尺寸（长×宽×高）为2 m×2 m×2.65 m，顶面毛细管网上层喷涂隔热层，下层使用黑网固定支撑，采用挤塑聚苯板填塞缝隙以保证气密性。实验小室各壁面的物性参数见表1。试验测试时间为2019年7月25日～8月8日，测试参数包括：实验小室内空气温度、小室内表面温度、毛细管系统供回水温度。

表1 实验室各壁面热工参数Tab.1 Thermal parameters of the walls of the laboratory

2.2 测点布置与试验仪器

图2示出了室内空气温度测点分布情况，在距离地面0.1，0.5，1.1和1.5 m的4个高度位置布置测点，每一高度处布置5个均匀分布的温度测点，共计20个室内温度测点以计算室内平均温度，测量仪器使用Hobo UX100-003温度记录仪，测量精度±0.21 ℃，仪器在试验前都进行过标定或校正，以确保测试数据可靠性，试验数据每10 min记录一次。

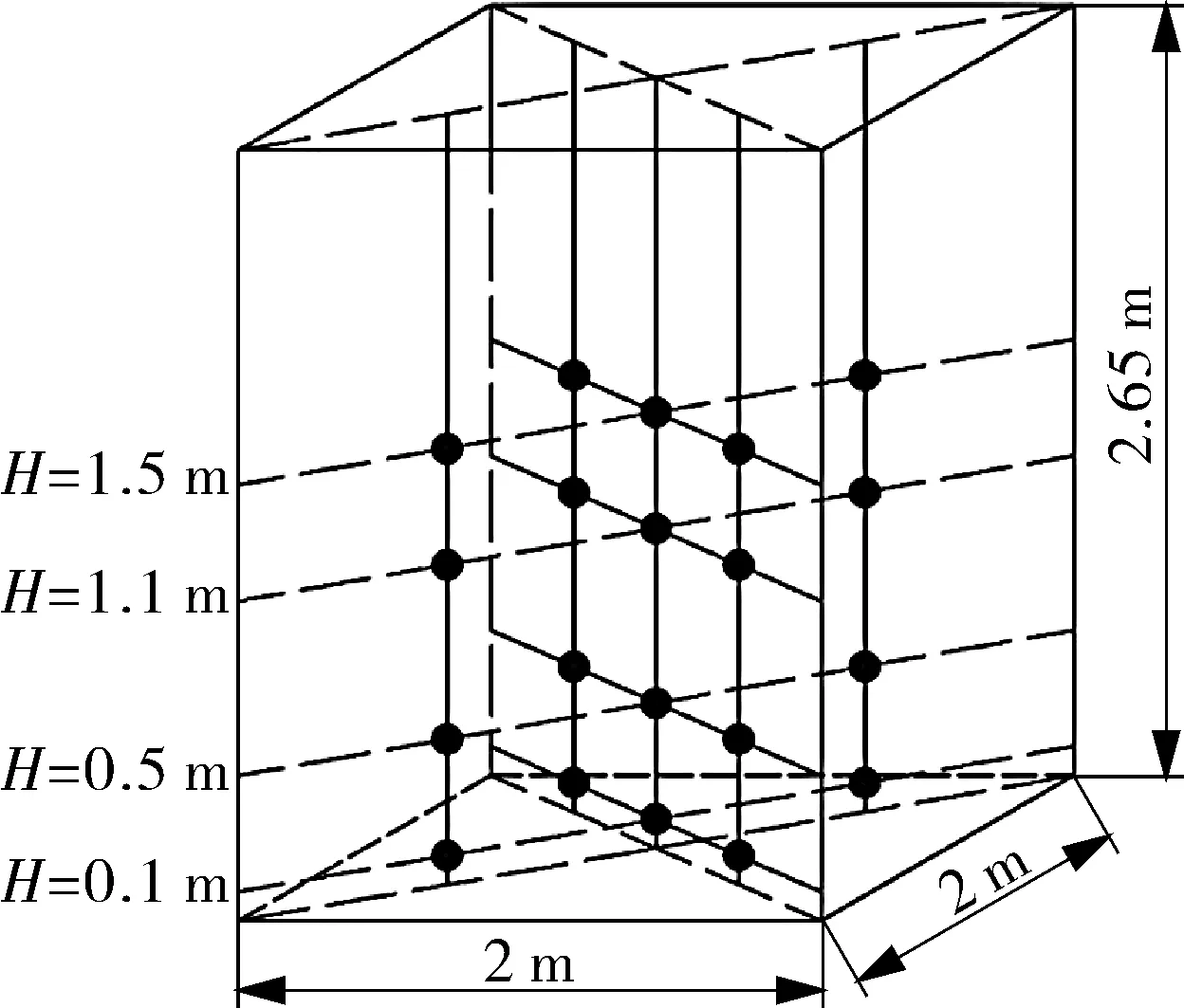
图2 室内空气温度测点分布Fig.2 Distribution of indoor air temperature measurement points

3 CFD模拟计算

末端传热延迟时间会随着围护结构热工参数、系统配置参数、供回水平均温度、初始室内温度等因素的不同而有所不同。通过实验测试方法研究末端传热延迟时间随影响因素的变化规律难度较大，CFD可以模拟流体详细的空间温度分布，相比于实验研究具有成本更低、周期更短的优势［8-10］，因此本文采用 CFD模拟的方法对该毛细管辐射系统在不同工况下的末端传热延迟时间进行研究。

3.1 模型建立和网格划分

根据实验小室的形状建立一个长×宽×高为2 m×2 m×2.65 m的简化3D几何模型，在ICEM中进行网格划分，采用结构化网格，几何模型上表面设定为冷辐射面，认为由毛细管和空气组成，由于冷辐射面的温度场变化较为明显。所以对冷辐射表面的网格进行加密处理，并进行网格无关性验证，以获得高质量的网格，网格划分结果如图3所示。

图3 CFD模拟计算网格划分Fig.3 CFD simulation calculation meshing

为了简化计算，对模型做出以下假设：（1）考虑浮升力作用，室内空气符合Boussinesq假设；（2）室内负荷仅由毛细管辐射末端消除，围护结构绝热；（3）每根毛细管道的入口参数相同；（4）毛细管网辐射表面温度是供水温度和回水温度的平均值；（5）毛细管内水的流动为恒定流动，其物性参数为常数。

采用FLUENT求解器进行非稳态计算，选择标准k-ε湍流模型模拟室内空气在浮升力作用下的自然对流，辐射换热通过离散坐标（DO）辐射模型模拟，采用SIMPLE算法求解压力-速度耦合问题，动量和能量方程采用二阶迎风格式求解。

3.2 边界条件

以毛细管辐射表面温度（供回水平均温度）稳定的时刻为模拟起点，根据试验测试结果，辐射表面温度稳定时对应的室内空气温度为26 ℃，相对湿度为42%，因此模拟的初始室内温度设置为26 ℃，对应各内表面温度的试验值作为边界条件的输入值，此时毛细管辐射表面温度为20 ℃，高于室内的露点温度12.14 ℃，不会出现结露现象，模型边界条件设置见表2。

表2 模型边界条件设置Tab.2 Model boundary condition settings

4 结果与分析

4.1 试验结果

以2019年8月8日为例，试验结果如图4所示，图中示出了供回水温度、不同高度处室内空气温度、围护结构内表面平均温度、地板温度随时间的变化曲线。

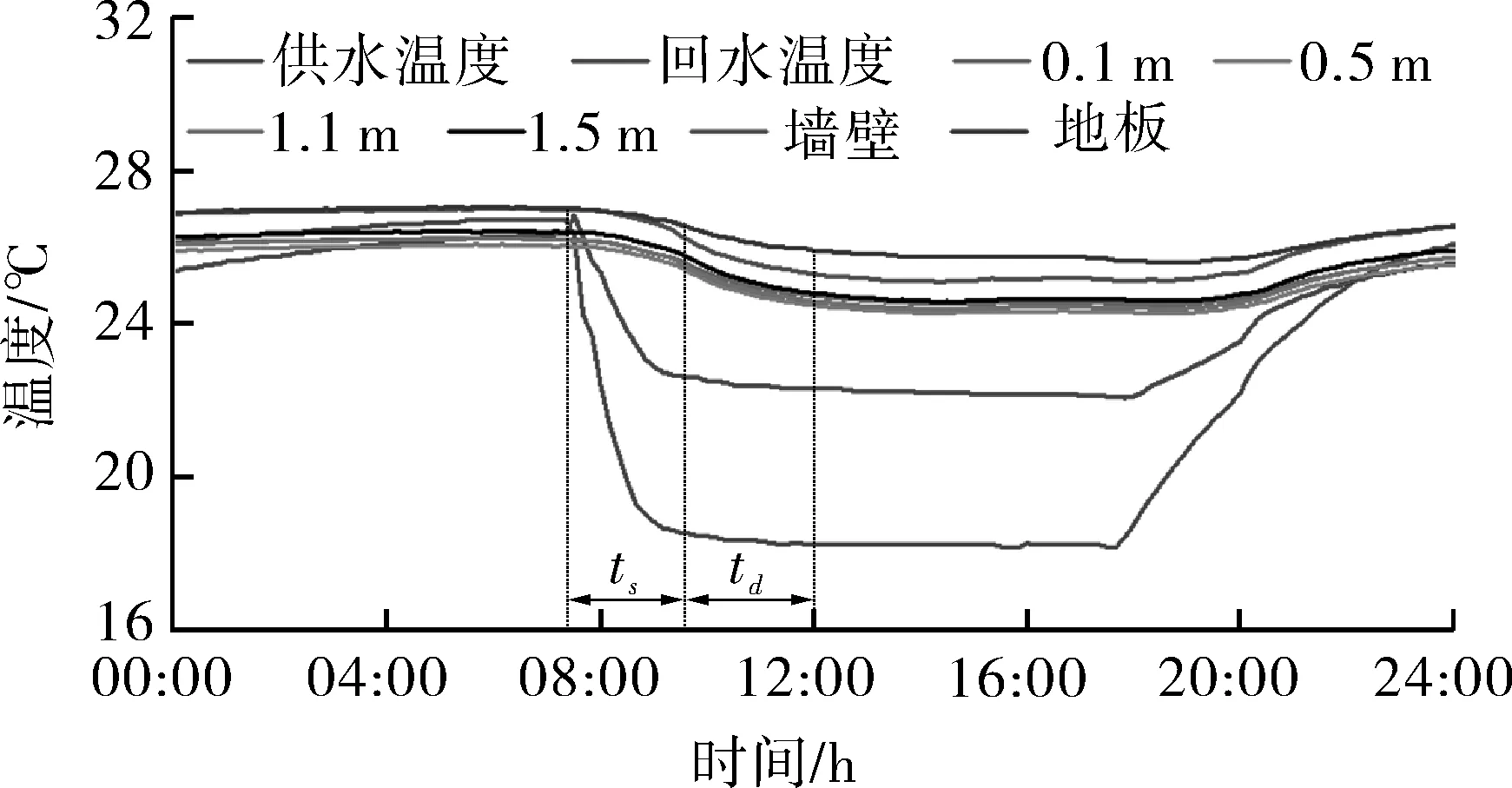
图4 各温度变化曲线实测值Fig.4 Measured values for each temperature change curve

可以看到机组在7：30启动，之后毛细管辐射表面温度随着供回水温度的降低而迅速降低，同时毛细管辐射表面通过长波辐射给其他内壁降温，由于热辐射和自然对流的影响，室内空气温度也逐渐降低。9：30供回水温度基本稳定，代表毛细管辐射表面温度达到稳定，之后内表面温度及室内空气温度继续下降，直到12：00左右基本稳定。因此通过试验可得该毛细管辐射系统响应时间 ts为 2 h（7：30～9：30），末端传热延迟时间 td为2.5 h（9：30～12：00），开启阶段建筑热响应时间tor为 4.5 h。

4.2 模型验证

图5示出了同一工况下室内空气平均温度试验值和CFD数值模拟值对比，图中0点对应CFD模拟的起始时刻，同时代表试验测试的9：30时刻，可以看到试验值与数值模拟值基本匹配，趋势相同，采用误差指标中的平均绝对百分比误差MAPE和均方根误差RMSE进行评价，2个误差指标定义如下：

图5 模拟计算与试验工况下的室内空气平均温度Fig.5 Average indoor air temperature under simulated and experimental conditions

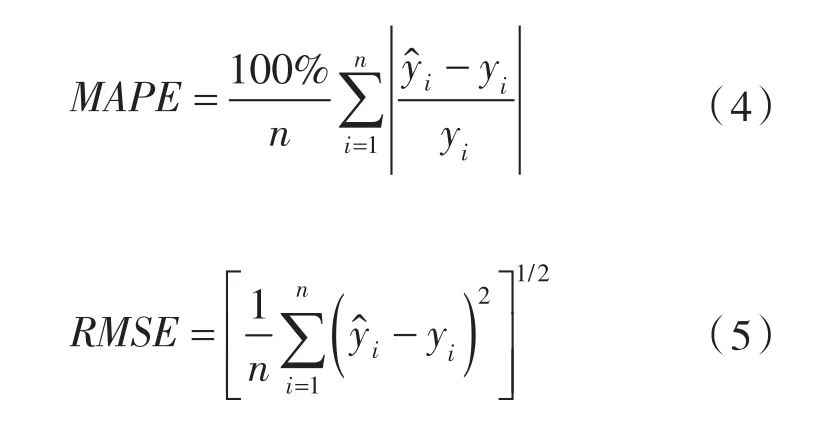
式中 n ——样本点的个数；

y ——试验值。

室内空气温度模拟值与试验值的MAPE和RMSE分别为0.62%和0.15 ℃，说明CFD计算中模型选择正确，边界条件合理。稳定后的室内热环境分布如图6所示，距离地面0.1，0.5，1.1，1.5 m的平均室内温度分别为 24.868，24.845，24.867，24.872 ℃，可见毛细管辐射系统可以提供均匀舒适的室内热环境。

图6 室内空气温度分布云图Fig.6 Nephogram of indoor air temperature distribution

4.3 影响因素分析

在既有建筑中，由于围护结构热工参数和系统配置参数已经确定不宜更改，所以本文只研究供回水平均温度和初始室内温度对毛细管辐射系统末端传热延迟时间的影响。在已验证的CFD模型中设置不同组合参数的工况，改变供水温度，恒定供回水温差4 ℃，以得到不同的供回水平均温度，考虑防结露问题，供回水平均温度的下限设为16 ℃，并与不同的初始室内温度进行组合，不同工况下的模拟条件和模拟结果见表3。

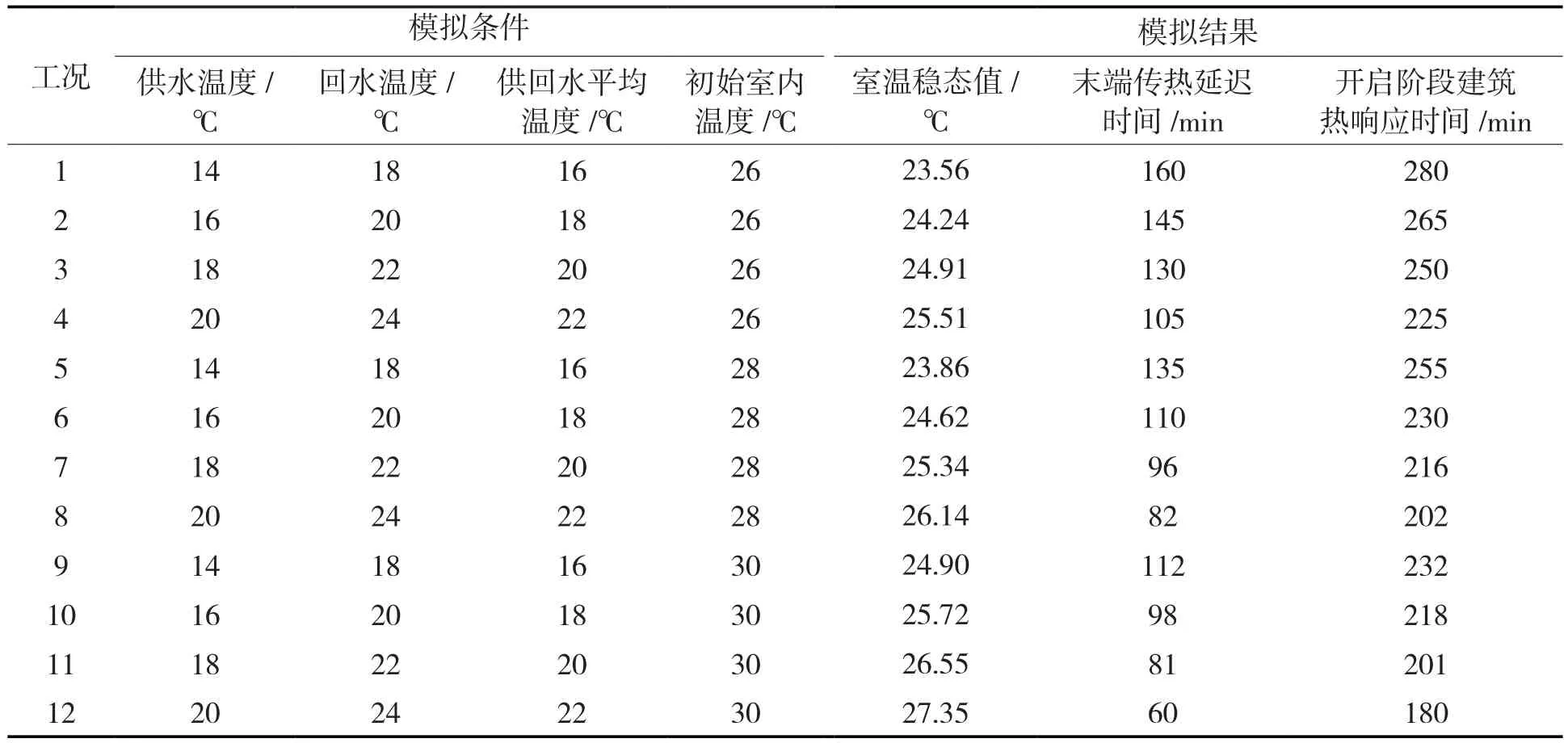
表3 不同组合工况下的模拟条件和模拟结果Tab.3 Simulation conditions and simulation results under different combinations of operating conditions

4.3.1 供回水平均温度

供回水平均温度即为辐射表面温度，图7示出了相同初始室内温度、供回水平均温度由16～22 ℃变化时的数值模拟结果。结果显示，在初始室内温度一定时，供回水平均温度由22 ℃降低到16 ℃，平均末端传热延迟时间由82 min增加到136 min，增幅65.9%。即相同的初始室内空气温度下，供回水平均温度越低，室内空气温度下降幅度越大，室温稳态值越低，末端传热延迟时间也越长。在初始室内温度为26，28，30 ℃时，供回水平均温度16 ℃相较于22 ℃，其室温稳态值各减小了 1.95，2.28，2.45 ℃，末端传热延迟时间各增加了 55，53，52 min。

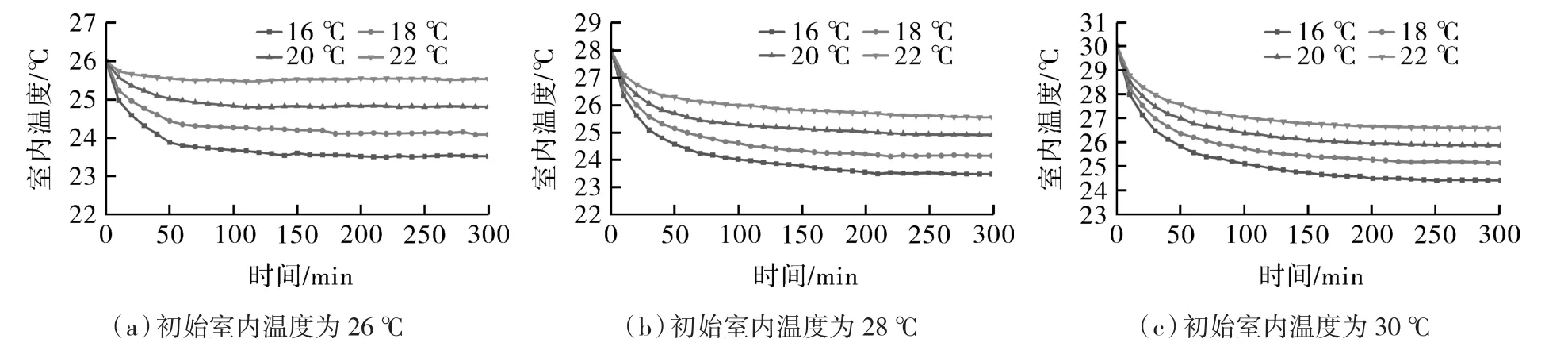
图7 供回水平均温度的影响Fig.7 Influence of average supply and return water temperature

4.3.2 初始室内温度

图8示出了相同供水温度、初始室内温度由26～30 ℃变化时的数值模拟结果。结果显示，在供水温度一定时，初始室内温度由30 ℃降低到26 ℃，平均末端传热延迟时间由88 min增加到135 min，增幅53.4%。即相同供水温度条件下，初始室内空气温度越低，室温稳态值越低，末端传热延迟时间也越长。在供水温度为14，16，18，20 ℃时，初始室内温度26 ℃时相较于30 ℃，其室温稳态值各减小了 1.34，1.48，1.64，1.84 ℃，末端传热延迟时间各增加了 48，47，49，45 min。室温达到稳定状态后，初始室内温度分别为26 ℃和28 ℃时，在不同供水温度下的室温都呈现逐渐相近的趋势。

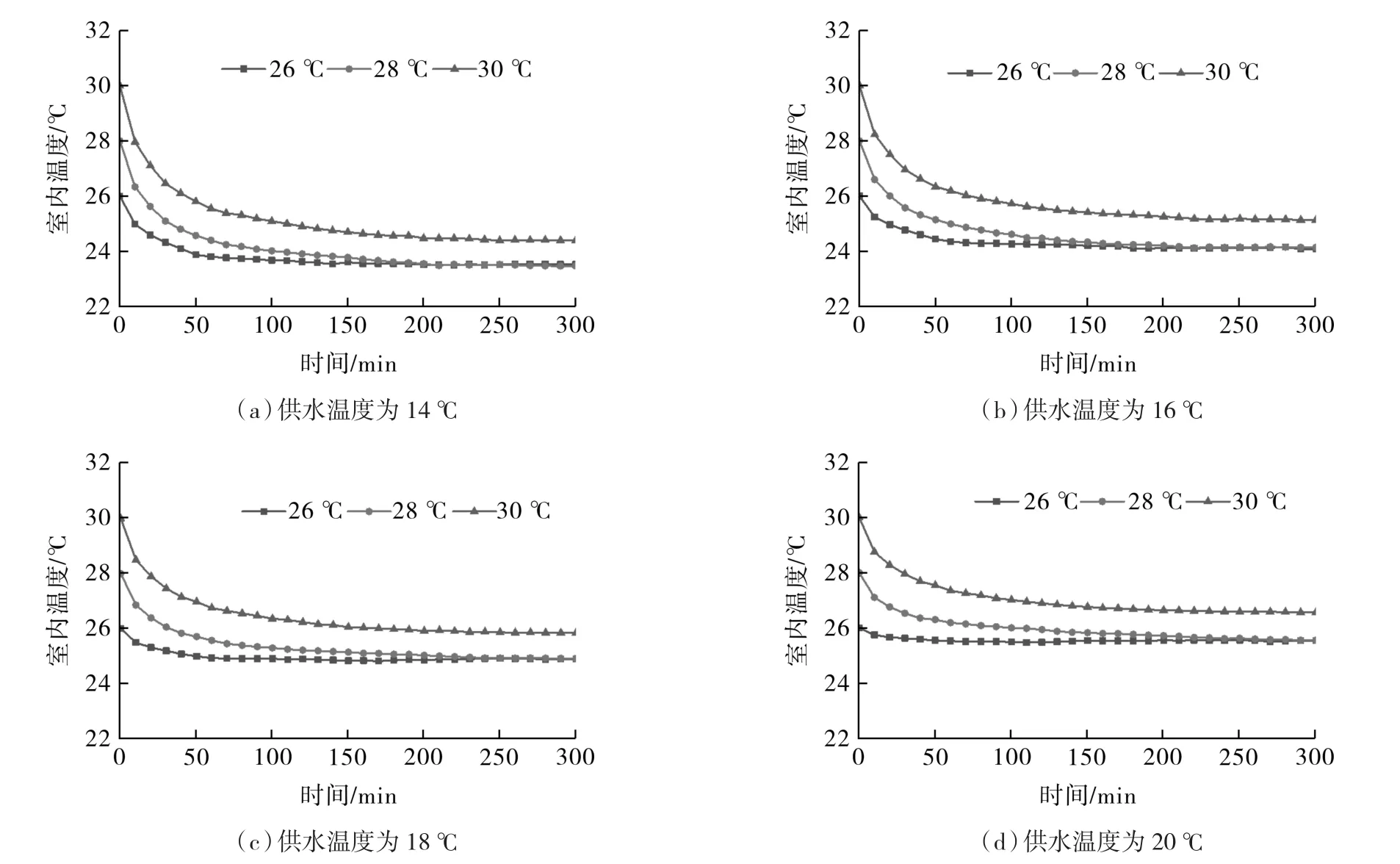
图8 初始室内温度的影响Fig.8 Influence of initial indoor air temperature

4.4 开启阶段建筑热响应时间计算模型

从以上模拟结果可以看出，不同的组合工况会导致不同的延迟时间及稳态热环境，但室内空气温度的变化趋势始终相似，毛细管辐射系统的热响应特性与供回水平均温度、初始室内温度之间有一定的规律。

采用SPSS软件根据试验结果和CFD模拟结果进行线性回归，整理出本研究案例中开启阶段建筑热响应时间与供水温度和初始室内温度的回归模型，见式（6）。图9示出了不同工况下该模型计算值与CFD模拟值的建筑热响应时间，可以看出，2种方法得到的建筑热响应时间数值接近，模型计算值与CFD模拟值的MAPE和RMSE分别为1.24%和3.70 min，且两者的相关系数为0.982 2，证明计算模型准确。由此计算模型可得，在初始室内温度一定时，供水温度每降低1 ℃，建筑热响应时间将增加约9 min；在供水温度一定时，初始室内温度每降低1 ℃，建筑热响应时间将增加约12 min。针对辐射式系统的热响应特性，可以根据计算的建筑热响应时间，确定系统的提前开机时间，使室内热环境达到要求。

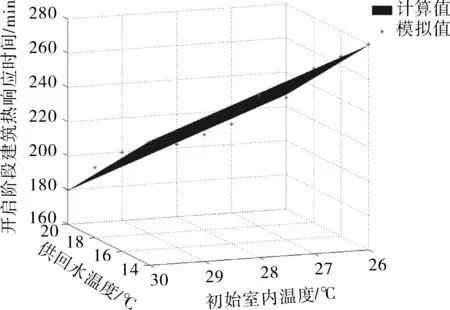
图9 模型计算值与CFD模拟值Fig.9 Model calculation values and CFD simulation values

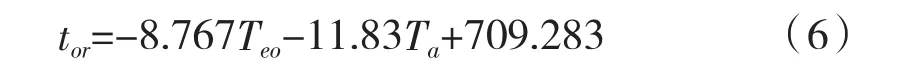
式中 Teo——供水温度，℃；

Ta——初始室内温度，℃。

5 结论

（1）针对辐射式供热供冷系统向室内传热存在的热响应特性，采用了试验测试和数值模拟相结合的研究方式，提出了系统响应时间、末端传热延迟时间、开启阶段建筑热响应时间的定义和计算方法。

（2）研究结果表明，案例建筑中毛细管辐射供冷的系统响应时间为2 h，末端传热延迟时间约为2.5 h，开启阶段建筑热响应时间约为4.5 h，因此，在夏季该系统宜提前4.5 h启动。在系统形式确定时，建筑热响应时间主要受供回水温度和初始室内温度影响，在供回水平均温度16～22 ℃、初始室内温度26～30 ℃范围内，供水温度每降低1 ℃，建筑热响应时间将增加约9 min；初始室内温度每降低1 ℃，建筑热响应时间将增加约12 min。

（3）本文建立的CFD模型可作为相关辐射式系统延迟时间研究的依据，建立的开启阶段建筑热响应时间计算模型，可为辐射系统提前开关机时间控制策略提供指导。