基于AHM和TOPSIS的电动汽车充电设施选址研究

张丽岩　杨颖　马健

摘  要：随着城市交通拥堵及环境污染问题的不断出现，优化电动汽车充电设施选址是基础设施建设的必然要求。文章结合充电桩选址的特点，从人口、规划、经济、交通等因素出发，建立了充电桩选址评价指标体系，并通过AHM模型确定各个对象层指标的权重，在充电桩需求量的基础上经过TOPSIS排序，得到所需充电桩站址，并进行实例分析。

关键词：充电桩选址;评价指标;AHM模型;TOPSIS排序

中圖分类号：U115    文献标识码：A

Abstract： With the continuous emergence of urban traffic congestion and environmental pollution problems， the optimization of ever charging facility site selection is an inevitable requirement of infrastructure construction. This paper established an evaluation system of site selection which is based on the characteristics of site testing such as population， planning， economy and traffic. The weights of each index are determined by AHM model. On the basis of the demand of charging piles， the required site of charging piles is obtained through TOPSIS sequencing and an example analysis is carried out.

Key words： charging pile site selection; evaluation index; AHM model; TOPSIS sorted

0  引  言

近年来，中国社会城市交通拥堵、城市污染严重及资源浪费的问题日益明显，共享经济不断发展，居民意识到绿色出行的重要性，我国新能源汽车数量快速增长，国务院常务会议强调支持新能源汽车产业与信息科技等产业高度融合，推进充换电基础设施建设，鼓励国际投资合作，加大对新能源汽车使用的政策支持。尽管如此，在电动汽车的发展与推广过程中，仍面临着巨大的问题挑战，尤其是普遍存在的电动汽车充电桩的规划建设与布局问题，一直制约着电动汽车的飞速发展。首先，部分发达城市等地区的电动汽车数量快速增长，但是充电桩建设规模严重不足，不能够满足城市居民需求。其次，在许多地区即使有政府政策的大力支持，人们对于电动汽车的接受程度仍然不高，使得电动汽车的增长总体情况仍有很大提升空间。最后，还存在充电桩客户满意度低、布局不合理、设施故障以及充电效率低等问题，导致充电设施的服务利用率较差。

科学合理地确定充电设施的位置及规模影响着充电桩的运营效益、充电效率、运营高效性、安全性以及客户满意程度等问题，对未来电动汽车行业规划发展以及居民生活便捷性、环保性有重要意义。因此，对于城市电动汽车充电设施的选址研究，提出充电桩选址评价指标体系以及选址模型，将为电动汽车充电桩的规划建设提供一定的理论参考，使城市充电桩选址更为合理，从而扩大城市电动汽车未来发展空间。

鲁莽等比较了电动汽车几种充电方式的特点，对未来我国电动汽车充电的商业模式及发展前景进行了初步研究[1]。赵明宇等通过分析电动汽车充电容量总体需求的影响，建立了以交流充电桩建设管理成本最小、电动汽车上路运营成本和充电等待成本为目标函数的交流充电桩建设模式，多场景运营模式和商业运营模式[2]。葛少云等人利用Voronoi图划分充电站服务区域，计算充电站服务半径，根据每个充电站的最大服务半径确定选址方案[3]。舒俊等用二进制代码对充电站的站点和容量进行编码，以生成初始种群，通过选择、交叉、变异等操作，找到适应度最高的个体作为全局最优解，即最优位置和容量[4]。Holzman讨论了在网络设施选址中，以用户与设施位置距离的平方和最小为目标，运用网络规划的基本原理建立选址模型，并结合具体情况进行了讨论和扩展[5]。

1  充电桩选址模型建立

充电桩选址评估主要包括三大步骤：首先，运用模型确定评价指标因素的权重;其次，设计评估方法对充电桩选址进行综合评价。基于本次评价的目的以及评价指标体系的特点分析，本文选择改进的属性层次模型AHM赋权法确定充电桩选址评价指标各因素的权重。接着利用TOPSIS，结合评价矩阵以及研究获得的各指标权重，获得最终选址结果。

1.1  建立充电桩选址评价体系层次结构

为了便于评价工作的实施以及评价数据的整理，使用AHM属性层次模型，将评价指标体系分为目标层A、准则层B、对象层C。

本文针对充电桩选址评价，评价指标的选取以苏州市充电桩的基本功能为基础，同时根据苏州市交通因素、公共设施因素、经济因素、客户服务要求等选出合理的评价指标准则层及对象层等，然后用AHM模型对对象层赋予权重，通过研究得出充电站选址评价指标体系，如表1所示。

1.2  构建两两比较判断矩阵及确定权重

在建立评价指标体系后，确定上下层指标之间的隶属关系。对于同一水平的指标，构造成对比较的判断矩阵，对指标的重要性进行比较，并按1～9的比例标度打分。

在属性判断矩阵中， 由层次分析矩阵中的比例标度a转化得到μ。转换公式为：

μ= （1）

其中：k为大于2 的正整数，β≥1，通常取β=1或2，当β→∞时，为极端情况;当a=k>1时，μ=1，当a=1时，μ=0.5，a<1时，μ=0。对于符合条件的μ为相对属性测度，并且由其组成的n阶矩阵为属性判断矩阵μ。

本文充电桩选址评价AHP与AHM判断矩阵如表2所示。

在层次分析法中，通过MATLAB软件计算判断矩阵的最大特征值λ=5.2012，根据式CI=、RI=、CR=CI/RI，对这一结果进行一致性检验，可得CI=5.2012-5/5-1=0.0503，根据“一次性指标对照表”可知RI=1.12，CR=0.0449<0.1，符合一致性要求。

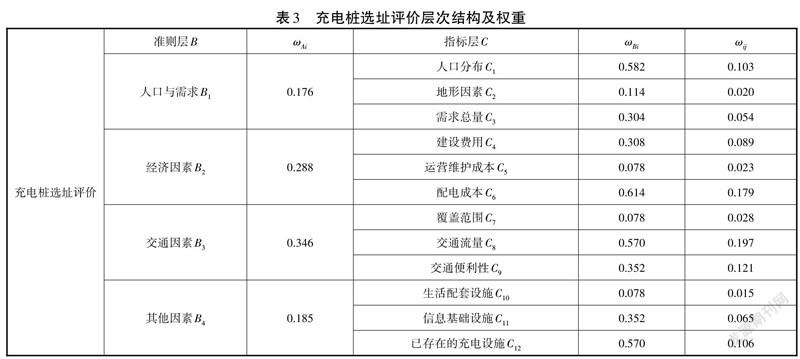
其中：根据ω的计算公式为：ω=∑μ，1≤i≤n，得到各个因子的相对权重值。用X代表对象层相对于目标的合成权重，则其计算公式表示为：X=ω1，ω2，…，ωn·Y，充电桩选址评价层次结构及权重如表3所示。

1.3  TOPSIS排序

利用TOPSIS，结合评价矩阵以及上文获得的各指标权重，获得最终评价结果。根据无量纲化、规范处理的决策值，依据

Z=Z，Z，…，Z，Z=max，Z=Z，Z，…，Z，Z=max，确定各个指标的正负理想点;计算参与综合评价的各对象站点与正负理想点的接近程度。

D=， D=

式中：ω表示第j个指标的权重;最后，通过计算参与综合评价的第i个选址对象与最优方案的贴近程度C，C=，所得结果C越接近于1，评价对象越优;根据C大小进行排序，得出总体评价结果，根据需求量预测规划区所需充电站数，得到最优充电站选址方案。

2  实证求解

在此，以某城市核心规划区为例，要在该城市核心规划区建设充电站并示范运行。经过初步筛选，拟定12个备选地址，按照顺序分别标记为地址U，地址U，地址U，……，地址U。根据《电动汽车充电基础设施发展指南（2015-2020）》，对我国电动汽车保有量的预测可得，2020年电动汽车的渗透率约为2%。经调查研究得知2018年某城市4个区域的燃油汽车保有量分别为35 730、53 782、63 314、47 782辆，按5%的年均增长率和2%的电动汽车渗透率计算可得2020年各区域汽车保有量和电动汽车数量，如表4所示。

电动汽车基建发展指南中规定，每2 000辆电动汽车至少配套建设一座公共充电站，由表4可知2020年该城市A、B、C、D交通小区电动汽车的总数目为4 014辆，应建设3座或3座以上的充电站，考虑到未来充电站的规划建设应适度超前，拟建4座公共充电站。直流快充和交流慢充按1∶4设置，直流快速充电桩的个数不少于95个。

2.1  指标下决策值

本次研究由20位专家对备选站址各项指标进行打分，打分采用5分制。评审专家由充电桩行业专家，物流、交通专业学生和使用电动汽车的用户组成，打分结果取平均值，由于不同类型会产生不同的打分结果，对指标数据进行规范化处理，结果如表5所示。

2.2  与正负理想点的距离

根据表5的规范化处理后的决策值，得到各指标与正负理想点距离，如表6所示。

由此可以确定各个充电桩选址方案U，U，…，U与正负理想点的距离，得到的综合排序结果如表7所示。

通过上述计算结果可知，U、U、U、U这4个站址为最佳充电站选址方案。

参考文献：

[1] 鲁莽，周小兵，张维. 国内外电动汽车充电设施发展状况研究[J]. 华中电力，2010，23（5）：16-20，30.

[2] 赵明宇，吴峻，张卫国，等. 基于时空约束的城市交流充电桩优化布局[J]. 电力系统自动化，2016，40（4）：66-70，104.

[3] 葛少云，李慧，刘洪. 基于加权Voronoi图的变电站优化规划[J]. 电力系统自动化，2007（3）：29-34.

[4] 徐凡，俞国勤，顾临峰，等. 电动汽车充电站布局规划浅析[J]. 华东电力，2009，37（10）：1678-1682.

[5]  Holzman D， Pope C， Xu X. An assoeialion between air pollution and mortality in six US cities[M]. New England J. Med.，1993：173-175.

[6] 宋亚辉. 城市电动汽车充电设施布局规划研究[D]. 北京：北京交通大学（硕士学位论文），2011.

[7] 周逢权，连湛伟，王晓雷，等. 电动汽车充电站运营模式探析[J]. 电力系统保护与控制，2010，38（21）：63-66，71.

[8]  Mohsenzadeh A， Pang C， Pazouki S， et al. Optimal siting and sizing of electric vehicle public charging stations considering smart distribution network reliability[C] // North American Power Symposium. IEEE， 2015.

[9]  Li Y， Li L， Yong J， et al. Layout Planning of Electrical Vehicle Charging Stations Based on Genetic Algorithm[M]. Electrical Power Systems and Computers. Springer Berlin Heidelberg， 2011.

[10]  Gao Y， Lu X. Analysis of the electric vehicle charging station's layout in Beijing based on improved traveling simulation model[C] // International Conference on Logistics， Informatics and Service Sciences. IEEE， 2016：1-6.

[11] 張粒子，舒隽，林宪枢，等. 基于遗传算法的无功规划优化[J]. 中国电机工程学报，2000（6）：6-9.

[12] 胡永宏. 对TOPSIS法用于综合评价的改进[J]. 数学的实践与认识，2002（4）：572-575.

[13] 邢芳芳. 区域电动汽车充电站布局优化研究[D]. 上海：东华大学（硕士学位论文），2017.

[14] 郑陈权. 城市电动汽车充电设施最优选址研究[D]. 南昌：南昌大学（硕士学位论文），2016.

[15] 林惠真. 电动汽车充电设施规划探讨[J]. 供用电，2012，29（3）：26-29，34.

[16] 高建平. 电动汽车充电站网络规划优化研究[D]. 济南：山东大学（硕士学位论文），2012.