数控机床时变切削振动自适应稳定控制方法

杨 柳

(陕西国防工业职业技术学院，陕西 西安 710300)

0 引言

数控机床作为主要生产设备，在机械加工中起到不可忽视的作用。但由于机床加工是一种动态变换过程，由于内部零件受损、受热变形和材料硬度不均等因素的影响，在时变切削过程产生剧烈的震颤，影响数控机床的生产质量、经济效益以及工作效率，长期的振动磨损还会导致机床及零件受损严重，降低使用寿命。为此，需要一种自适应稳定控制方法来约束机床时变切削的振动。

文献[1]提出基于机床运行状态的切削振动控制方法，难以随时追踪信号的变化，频域判定的精准度低；文献[2]基于振动特性分析的主动抑制方法，但没有考虑到外界因素的影响，导致判定的振动分量中存在一定的噪声因素，状态局限性高、误差较大。综合上述问题，本文采用时变模态分析实现切削振动自适应稳态控制，分析机床在切削过程中影响稳定性的转子参数，静态表示参数后再利用模态分析法简化需要控制的切削分量，该过程可剔除一定的噪声数据保证后续控制的稳定性。最后，凭借数控机床在加工过程中，切削条件是不断变化的这一时变特点，准确修正实际切削用量，改善因切削用量不均带来的强震问题，为数控机床的高速及高效运作提供重要帮助。

1 数控机床时变切削工作过程振动性

数控机床时变切削振动控制的基本内容：以机床本身、切削刀具以及工作系统为主要对象，凭借特定模型对工作过程中产生的高频振动[3]信号进行控制，降低损耗。通过分析一般机床在切削运作时位移及速度的变化，利用反馈回路[4]精准判定受干扰较强的位置，对该位置进行高强控制。机床切削工作过程模拟如图1所示。

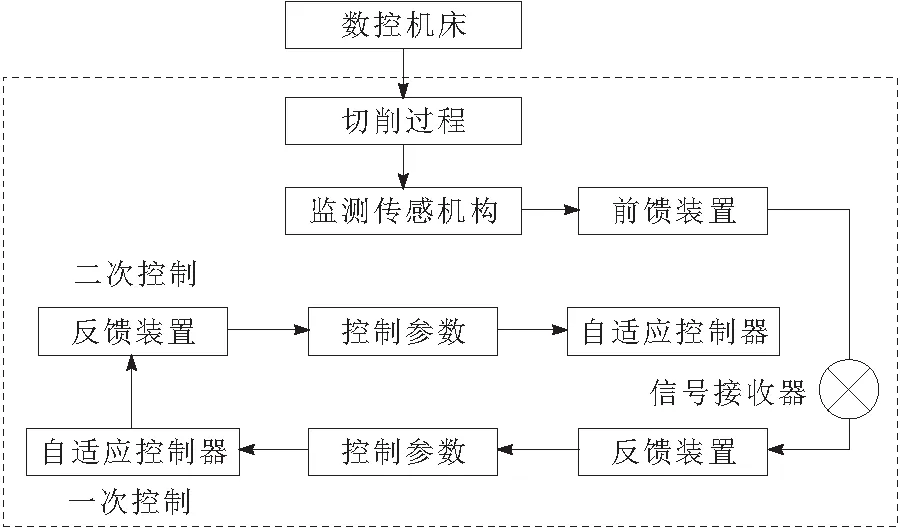
图1 数控机床模拟时变切削过程

从图1可以看出，数控机床的切削过程主要由监测(传感器)装置、前馈装置[5]、反馈回路装置和控制机构组成。当监测装置发现高频振动时，将关键参数以及等级评价等信息传递给控制结构，控制主机启动，输出校正信号[6]，通过条件转变使得机床运作可达到最佳状态。将上述过程所需的信号、转子和算子等参数利用公式进行表达，后续过程就可根据对应参数进行自适应控制，提高准确性。

在图1中的伺服环节可利用二阶系统来具体表示，即

(1)

s为Laplace变换运作算子；u(s)为伺服结构的初始输入值；Kn为伺服平均增益数值；ωn为伺服机构[7]工作的平均频率；v为切削递进的初始速度；ξ为摩擦系数[8]。将切削递进的初始量设为f，可以得到

(2)

m为数控机床切削主轴的转速；b(s)为切削带宽；pn为切削刀具的锯齿数[9]。

考虑到图1中参考控制模型是一种理想型的调节机构，没有代入环境及人为因素的影响，所以将式(1)进行状态调整使其更符合实际情况，即：

(3)

Fs=Ksafo=(Ksafo·1)f

(4)

Ks为综合静态切削力；o为运行指数(正常情况下o<1)，Ks和o的取值都由刀具的形状和材料共同决定；a为刀具的背吃量[10]。

根据数控机床的不同加工特性，设运行指数为o=1，此时切削工作的动态过程Fs为

(5)

ts为切削工作的时间常数。根据上述过程，计算得出数控机床在工作时产生的切削系数，对应给出下一步的具体振动控制计划，提高控制精准度和稳定性。

2 基于时变切削振动的模糊稳定性分析

将上述过程给出的切削振动关键参数利用模糊稳定法，建立基于模糊动态的振动表达模型[11]，通过模型详细计算切削振动影响较大的因素，并归一化处理保证自适应控制的统一性。

将数控机床的切削结构看作是一个包含多种自由度的运动系统。当发生切削振动时，其自由度数值一定会发生变化，模态振动表达模型为

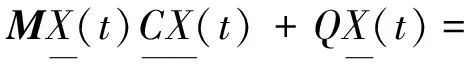
(6)

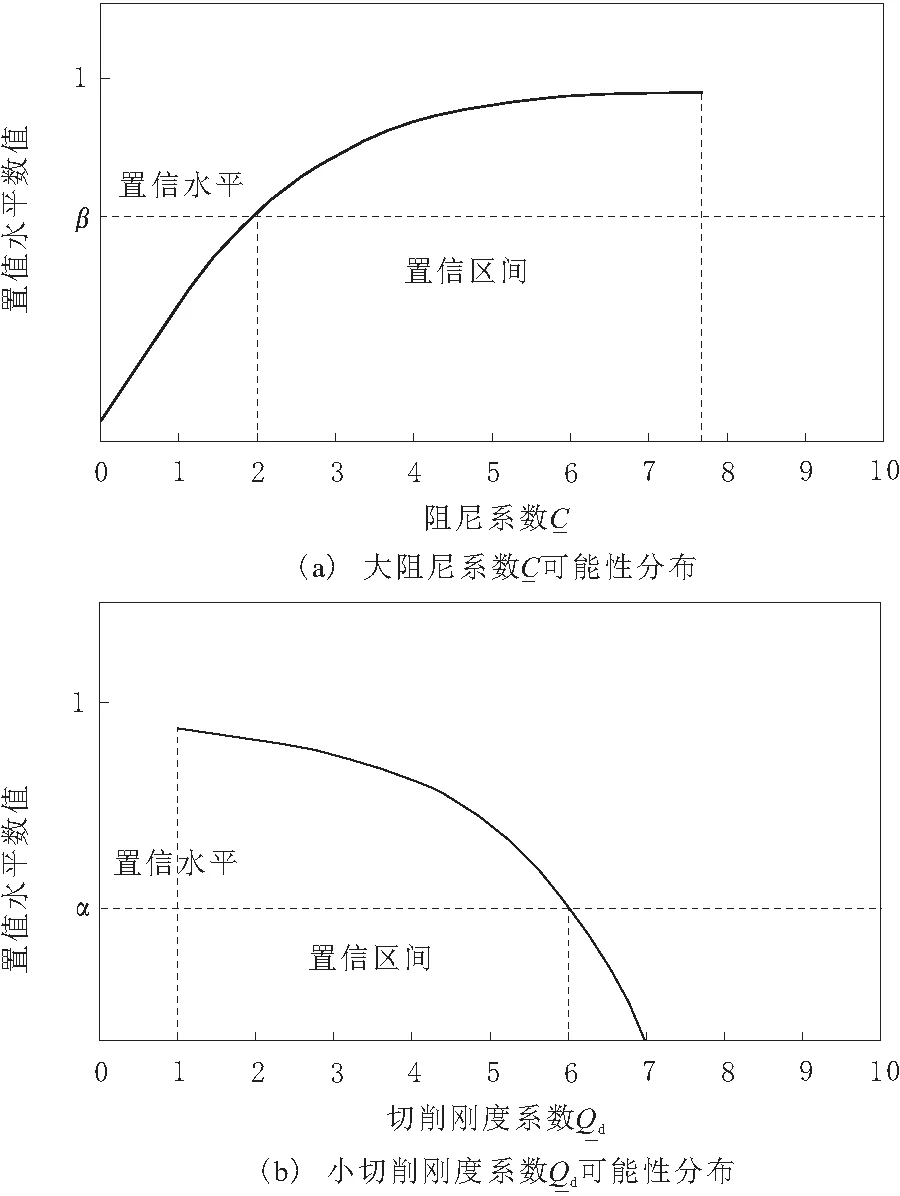
图2 不同系数对切削振动的影响分布

(7)

(8)

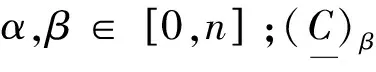
(9)

δ∈[2,7.5]为阻尼系数的置信区间[14]；δ∈[1,6]为刚度系数的置信区间。在该区间内的阻尼和刚度系数就属于正常振动范围，如果超出该区间就需要及时进行自适应控制，保证工作效率及安全。

3 数控机床时变切削振动自适应稳定控制方法

以上述过程计算得出的模糊集合和置信区间为基础，利用平面坐标系来模拟机床切削振动时发生的位移关系。将时变切削振动可能出现的位移方向用X+、X-、Y+、Y-表示，当高精密无线传感器实时监测发出振动时，记录这4个方向上的时变位移。将位移信号作为模态函数的输入数值，利用逼近函数约束输出的数值状态，使其符合控制条件。同理，得到的关于声音信号的逼近函数[15]，也进行自适应控制，最终获得符合条件分布相关参数。

在坐标系X+的方向上，控制对象的位置信号捕捉表达式为

(10)

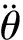
(11)

b(s)为切削宽度；Pe为切削功率；x1为位移信号变量的最高峰位置；x2为声音信号变量的最高峰位置。根据式(11)设计一种模态控制函数g(x)为

(12)

η为位移变化的界定值；g(x)为模态控制函数，此时，有

(13)

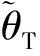
4 仿真实验

4.1 实验设置

本次实验设备选用的是某机械加工场内的西门子立式5040号数控机床，机床工龄为5年，内部的工件、切削刀具以及动态滑轮运行稳定。主轴切削运行的平均转速为m=400 r/min；切削宽度为b(s)=12 mm；切削功率为Pe=3 kW；切削方向为由中心逐渐向外切削。采用仿真形式模拟切削过程，切削量随时间变化而不断增强直至发生剧烈震颤，重复该过程直至实验完成。

通过上述实验测试后，将振动参数代入式(11)中，可得到

(14)

利用MATLAB中的Sources模块库进行切削振动信号仿真，提取位移和声音2种频域信号。式(14)中，位移信号变量的最高峰位置x1=2.5 Hz；声音信号变量的最高峰位置x2=10×10-2Hz；u为均衡参数。可通过对比各种方法的实验结果是否超过最高峰幅值x1和x2，来判定对数控机床时变切削振动的控制效果。

4.2 基于位移信号的振动控制结果

通过数控机床切削振动的位移信号分析本文的自适应控制效果，实验结果如图3所示。

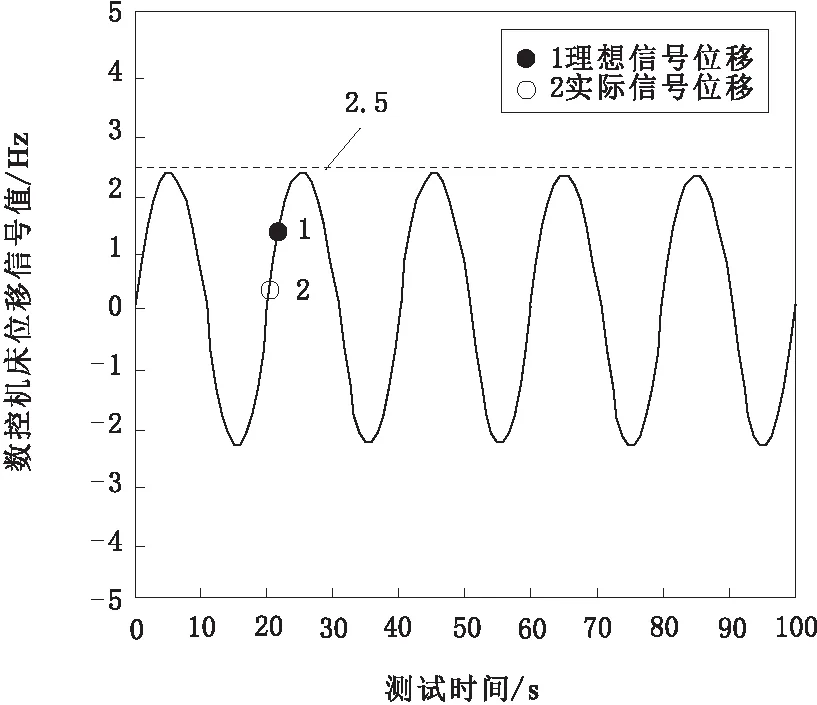
图3 切削振动位移信号变化结果

由图3可以看出，曲线处于一种稳定波动状态，没有较为突出的变动峰值，相邻规律时间内上下幅值位置基本保持一致。且实际跟踪位移和理想位移都处于曲线上，保持一种前后跟进的状态，最高峰值没有超出规定值x1=2.5。说明本文方法可以有效控制切削振动问题，使得控制对象可以按照安全规定或理想的位移方向进行移动，保证状态稳定的同时还能提高系统运行的鲁棒性。同时，不受外界噪声信号的干扰，避免控制切削工作中由于强震位移引起的财产损失和人员伤亡问题。

4.3 基于声音信号的控制结果对比

以数控机床切削动态工作时检测的声音信号为判定依据，与运行状态切削振动控制法、特性分析切削振动控制法进行对比分析，得出实验结果如图4所示。

从图4可以看出，图4a和图4b的声音频域信号整体较为混乱，信号幅值变化较大，在前半部分的测试时间内波动尤为明显，不具有一定的对称性和规律性，最高峰的信号幅值也超过了规定值x2=10×10-2Hz。说明这2种方法对数控机床切削振动控制效果较差，振动表达不一，导致声音信号的强弱不断发生变化，稳态性较差。出现这种现象的主要原因是：没有考虑到切削刚度及宽度等关键参数的影响，刚度和宽度不一致都会导致振动频率出现不稳定现象，并产生大量噪声信号，干扰自适应控制点的捕捉和实施强度。

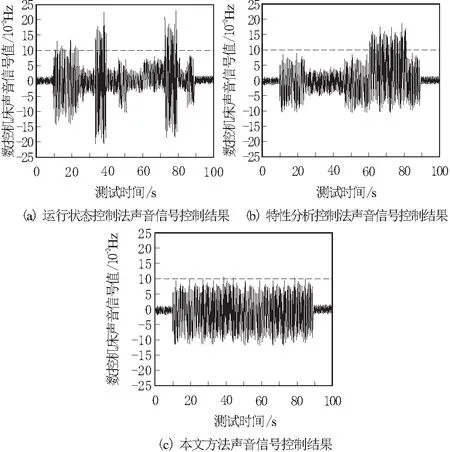
图4 3种方法基于声音信号的控制结果对比

反观图4c本文方法，声音频域信号整体变化较为稳定，取任意一点作比较，都具有较强的对称性。单位测试时间内信号差值较小，最高峰值没有超出规定值x2=10×10-2Hz。说明本文方法对数控机床切削振动具有可观的控制效果，可降低设备损耗和不稳定性，避免由强震造成的伤亡及财产损失问题，提高工作质量。

5 结束语

本文提出数控机床时变切削振动自适应控制方法。为了能更加适用于实际的机床切削情况，通过模拟分析机床切削的加工过程，得出阻尼系数、刚度、带宽和转速等关键性参数，帮助下一步基于模糊动态振动力学模型的分析与计算。力学模型给出了切削振动的界定标准，超过该值会立即启动控制装置，根据此特点，本文从切削振动的位移信号和声音信号2个方面入手，利用模态控制函数实现了精准控制，使得切削工作能在极短的时间内逐渐趋于稳定，属于一种柔性控制，给系统适当适应的时间，不会过于迅速导致急停等危险现象发生，能够证明所提方法鲁棒性及稳定性较强，可为机械生产提供有效帮助。