齿面干涉图像的相位解包裹算法对比研究

梁蒲佳，许 涛，杨鹏程，徐 晋，王兆辉

(西安工程大学机电工程学院，陕西 西安 710048)

0 引言

精密齿轮是机械传动系统中的重要零件，其形状误差是影响传动精度的重要因素[1]。通过激光干涉测量系统来获取齿面干涉条纹图像后，经过相位提取、相位解包裹和配准等步骤来得到齿面误差信息。其中相位解包裹是整个激光干涉测量技术的关键环节，包裹图携带着齿面的全部信息，解包裹质量的高低将直接影响到最终测量精度。从齿面干涉条纹图像中提取的相位值是由反正切函数的形式表示的，其相位值是被截断、或者说被包裹在(-π，π]的主值区域内，为得到真实值，必须将截断的相位恢复为连续的状态，这个过程称为相位解包裹[2-3]。相位解包裹应用场景非常广，有合成孔径雷达测量、光学干涉测量、摩尔测量、核磁共振成像和结构光投影测量等[4-7]。

1986年，Goldstein[8-9]提出路径跟踪的枝切法来解包裹。1991年，Bone[10-11]提出的质量图引导法有效的避免了枝切法中由于枝切线闭合导致的“孤岛”现象。1994年，Ghiglia[12]等在非加权最小二乘法的基础上提出加权最小二乘法，抑制了误差的传递。2002年，赵争等提出的遗传算法以及2008年魏志强等提出的蚁群算法被引到枝切法中，优化了枝切线的放置[13-15]。2012年，李芳芳等[16]根据质量图引导提出快速相位解缠法，对解缠效率有所提高。2016年，Backoach等[17]利用计算机图形处理单元并行处理离轴全息图中的相位信息，用来捕获具有快速鞭毛运动的微生物干涉成像相位图。2019年，赵振强等[18-20]提出基于深度学习的InSAR相位解缠算法。在过去的几十年，相位解包裹技术一直是研究的热点，但是由于各个领域干涉图像特征的不同，使得目前并无通用的解包裹算法。

对于精密齿轮在加工和使用过程中形成的形状误差使得齿面干涉图像具有局部散斑、边缘杂散条纹、疏密不均和粘连等特征，目前并无通用的算法，也没有统一的数据集，所以依然依托于经典算法来寻求一种适用于齿面形状误差测量的解包裹方法用于后期改进。根据已有的经典算法，选取枝切法、相位导数偏差的质量图引导法、最小二乘法、傅里叶变换轮廓术和傅里叶变换的质量图引导法对齿面干涉图像进行解包裹实验分析比较，相位导数偏差的质量图引导法解包裹的灰度图以及相位数据图相比于其他算法更加平滑，能更好地处理齿面干涉图像中噪声严重的问题。

1 经典解包裹算法实现

1.1 枝切法

枝切法[21-23]是经典的路径跟踪法。首先，实际测量情况下，相位数据获取过程中会受到噪声的影响而出现非连续点，把这些非连续点在包裹相位图中标记为残差点(正负极性电荷)；其次，为了平衡全图的残差点，将正负残差点进行配对，在配对连接的过程中要注意枝切线要尽可能的短；之后，从包裹相位图中某一非残差点位置开始向四周方向进行解包裹操作，若遇到枝切线上的点则绕过此点继续进行正常相位点的解包裹，直至全图所有正常相位点完成解包裹；最后，通过分析枝切线周围的正常点相位信息对枝切线上的相位进行解包裹。

其中，残差点计算表达式为

(1)

φ(i,j)为包裹相位图上i行j列的相位值；W为相邻相位差。Δi的和为残差点，和记作q，如果q为2π的正整数倍，则称为正残差点，值设为+1；反之，为负残差点，值设为-1。

其中，q的表达式为

(2)

其算法流程如图1所示。

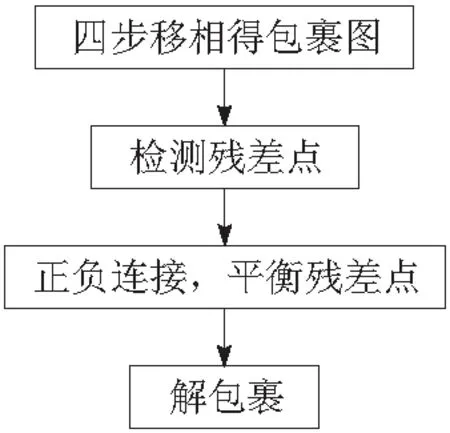
图1 枝切法算法流程

枝切法计算效率非常高，在残差点不集中的情况下，可以解决绝大多数包裹相位的包裹，但是在残差点比较集中的局部区域，容易因为枝切线放置环绕形成封闭的“孤岛”区域，使得解包裹结果出错。

1.2 相位导数偏差的质量图引导法

相位导数偏差的质量图引导法[24-28]是通过相位差分偏差法先建立一个可以表示包裹相位图各点的质量好坏的质量图，再以该质量图为解包裹引导路径，沿着质量从高到低有序解包裹，直到所有的包裹相位被解开为止。

首先通过相位导数偏差法建立质量图，表达式为

(3)

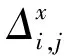
(4)

(5)

W为将计算结果限制在(-π,π]的包裹算子。

这里对相位导数偏差的数值进行了取反操作，因为相位导数偏差法计算的数值大小与相位质量的是反相关的，取反后，其数值就与相位质量正相关。

相位导数偏差的质量图引导法的算法流程如图2所示。

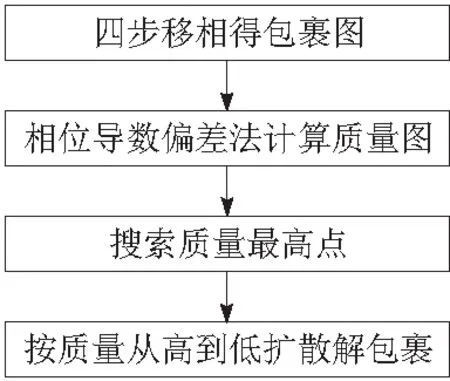
图2 相位导数偏差的质量图引导法的算法流程

相位导数偏差的质量图引导法跟枝切法一样也是将残差点放在最后解包裹，不同的是利用相位导数偏差法将包裹相位图每个像素按照质量高低排序后再从高到低扩散式进行解包裹操作的，理论上更优于枝切法，但是更耗时。

1.3 最小二乘法

最小二乘法[29]主要是计算待求相位与包裹相位之间的相位梯度误差的最小二阶范数，从而获得待求相位的逼近值，表达式为

(6)

Φi，j为待求相位；M，N为包裹相位的像素点M×N；

最小二乘法的算法流程如图3所示。

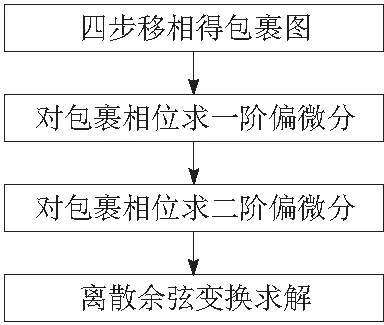
图3 最小二乘法的算法流程

最小二乘法属于路径无关算法，是全局意义下的最优化问题。对于干涉图像残差点有很好的抑制效果，采用经典的高斯-塞德尔松弛算法进行迭代，但其收敛速度非常慢，实际求解采用离散余弦变换。

1.4 傅里叶变换轮廓术

傅里叶变换轮廓术[30-32]最早是在1983年由日本的Takeda和Mutoh提出来的，开始应用于物体的三维形貌测量。傅里叶变换轮廓术是利用投影仪将正弦条纹投影到被测物体上，用CCD相机拍摄被测物体高度调制的变形条纹；再将变形条纹图像通过傅里叶变换从空域变换为频域，通过滤波将噪声滤掉，保留包含物体高度信息的基频信息；再通过逆傅里叶变换得到变形条纹的光强分布，通过反正切计算获取变形条纹的包裹相位；最后再进行解包裹操作得到被测物体的高度信息。

将此方法运用到激光干涉领域，就是将投影得到的变形条纹图像替换为由本激光干涉测量系统拍摄得到的齿面干涉图像，具体实现流程如图4所示。

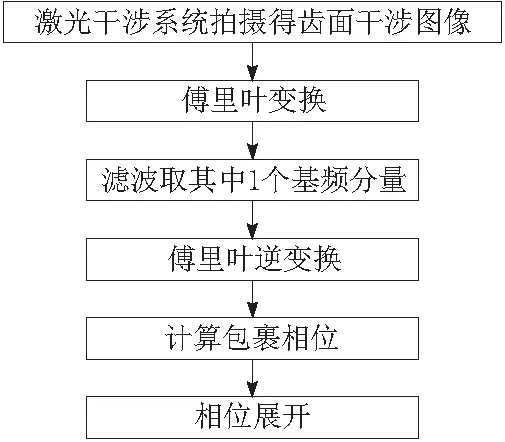
图4 傅里叶变换轮廓术流程

傅里叶变换轮廓术包裹相位只需1个干涉图像就可以获取，但傅里叶变换是全局的分析方法，如果齿面剧烈变化则不能保证包裹相位获取的正确性，而且在提取基频分量时，容易出现频谱混叠，同样不能获取正确的包裹相位。

1.5 傅里叶变换的质量图引导法

此方法[33-35]是傅里叶变换轮廓术和质量图引导法的结合，通过对干涉条纹图像进行快速傅里叶变换，对频谱图进行高通滤波滤掉噪声和背景，再进行傅里叶逆变换，通过调制度法计算质量图。此时调制度与相位质量成正比例关系，也就是说干涉条纹图调制度越高的像素点，相位质量越高。以计算的质量图为引导路径，沿着质量从高到低有序解包裹，直到所有的包裹相位被解开为止。具体实现流程如图5所示。

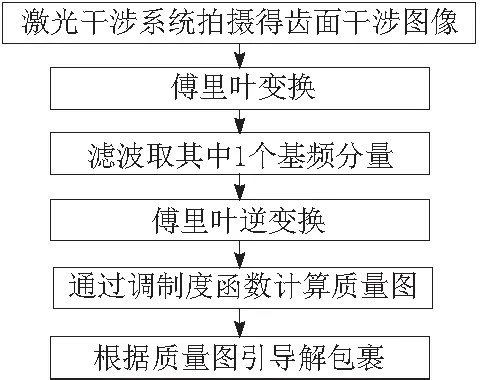
图5 傅里叶变换的质量图引导法流程

其中，调制度函数为

(7)

Re[b(x,y)]为傅里叶逆变换后的实部；Im[b(x,y)]为傅里叶逆变换后的虚部。

傅里叶变换的质量图引导法同样具有傅里叶变换轮廓术的优缺点，齿面缺陷以及提取基频时出现的频谱混叠将直接影响到质量图的优劣。

2 实验对比

激光干涉测量系统如图6所示。利用该系统，采用四步移相法，移相器步进π/2拍摄了一系列齿面干涉图像。为检验各解包裹算法在本测量系统中应用效果，选取了原始大小为1 240×290像素的1组齿面干涉图像(如图7所示)作为实验对象，计算包裹相位(如图8所示)后进行解包裹处理，对各个算法的解包裹结果进行对比和总结。

图6 激光干涉测量系统

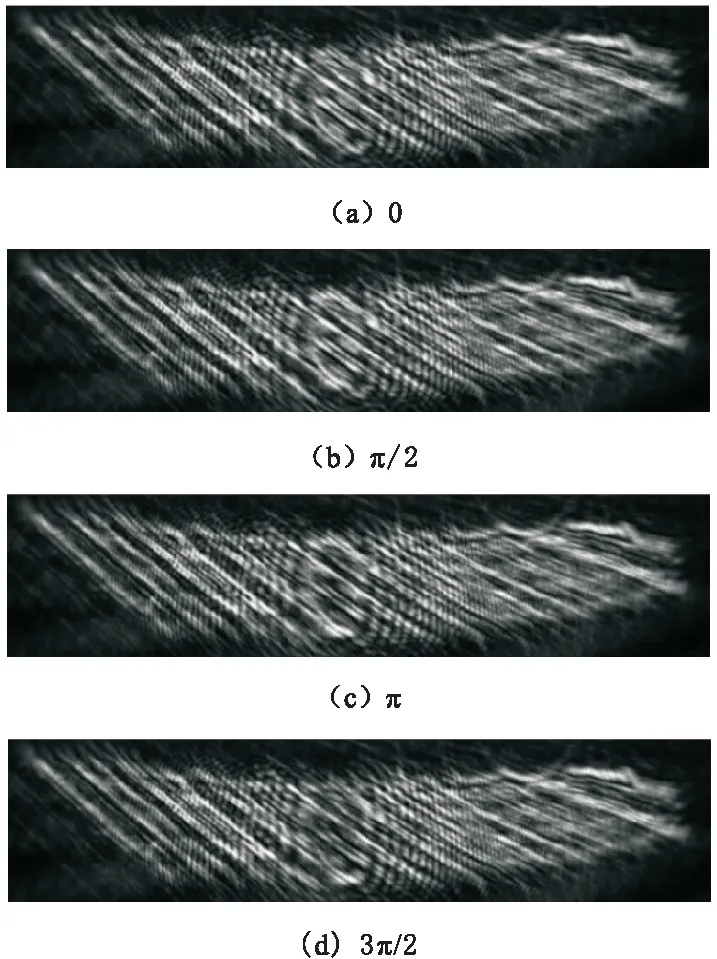
图7 齿面干涉图像(四步移相法)

采用第1节所述方法进行解包裹操作，结果如图9所示。从解包裹结果灰度图情况来看，枝切法(图9a)结果图出现灰度较低的点，称为无法解包裹的“孤岛”区域。傅里叶变换轮廓术(图9d)结果图灰度有明显差异。相位导数偏差的质量图引导法(图9b)、傅里叶变换的质量图引导法(图9e)、最小二乘法(图9c)3种方法灰度比较接近，但傅里叶变换的质量图引导法相比于相位导数偏差的质量图引导法灰度仍有起伏。最小二乘法(图9c)本质上是二维的最小二乘拟合，如果包裹相位数据存在残差点，那么解包裹结果会存在扭曲现象，为此对最小二乘法进行反包络。反包络后的相位图(图10)与原始包裹相位图(图8)相比，重新包裹后的相位图条纹扭曲严重，而测量对象是精密齿轮，要求每一点的解包裹结果都是精确的。因此，最小二乘法暂不适用于本课题，后面不再对其进行讨论。

图8 包裹相位图

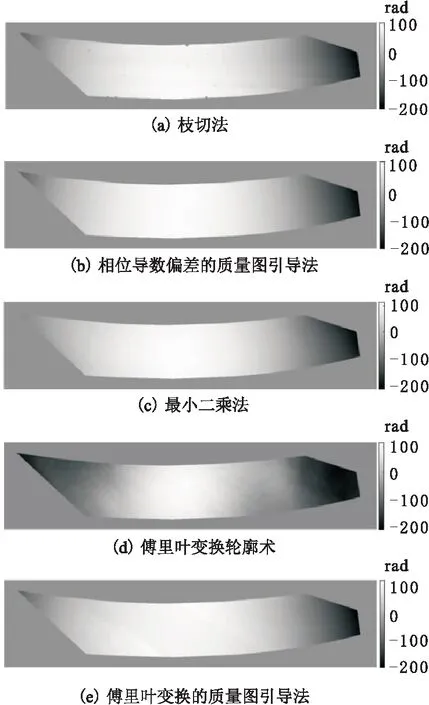
图9 相位解包裹结果

图10 反包络后的相位图

这里提取出各算法解包裹结果图中第130行的相位数据用来定量说明，如图11所示。

图11 130行解包裹相位数据曲线

由于齿面干涉图像局部区域噪声影响，致使局部枝切线比较密集，最终导致枝切法解包裹结果出现“孤岛”区域，如图11a中a,b此2点处的相位值。傅里叶变换轮廓术解包裹相位图曲线(图11c)整体趋势上有较大波动。傅里叶变换法的质量图引导法解包裹相位图曲线(图11d)在cd段出现波动。相比之下，相位导数偏差法的质量图引导法对齿面干涉图像噪声有更好的抑制作用，其解包裹相位曲线(图11b)更加平滑，解包裹精度高。

3 结束语

针对激光干涉测量系统采集到的齿面干涉图像，相位导数偏差的质量图引导法在处理齿面干涉图像的噪声问题上可以得到理想的解包裹结果。枝切法由于齿面干涉图像中局部散斑、边缘杂散条纹、条纹粘连等噪声使得枝切线封闭形成“孤岛”区域，导致解包裹结果出错。傅里叶变换轮廓术由于齿面干涉图像中条纹疏密不均以及噪声的影响造成解包裹结果出现大面积错误。傅里叶变换的质量图引导法计算质量图的方法与傅里叶变换轮廓术是同样的思想，同样的原因导致计算的质量图较差，最终解包裹结果出现局部错误。综上，相位导数偏差的质量图引导法更适用于处理齿面干涉图像，后期改进也将主要基于此方法继续展开研究。