盾构机盾尾变形检测与有限元分析

孙海力，吴恩启，闵 锐，吴天华

(1.上海理工大学机械工程学院，上海200093； 2.上海隧道股份机械制造分公司，上海200137)

0 引言

近年来，随着城市建设规模的不断推进，以轨道交通为主的地下空间开发得到空前发展。盾构法具有对周围环境影响小、掘进速度快等优点，所以广泛应用于地下土木工程的建设[1-2]。然而在实际施工过程中，盾构机壳体由于受水土压力、地质状态变化等影响，不可避免地会发生一定程度的弹塑性变形，特别是弹性变形，由于盾尾内部结构中没有支撑桁条，相较于其他部位更容易发生变形[3]。如果盾尾变形过大，会导致盾尾与管片之间间隙过小，造成两者的磨损，增加盾构阻力或损坏结构，严重时无法正常施工，影响施工进度，甚至对地面沉降造成严重影响等危害[4]。

国内外学者针对盾尾的变形及间隙评价进行了相应的研究。张雪辉等[5]分析了不同结构的超大直径盾构机的盾尾在水土压力下的变形及应力分布状况；Han等[6]分析了盾尾变形的特点及原因，采取措施实现了回弹；Guo等[7]设计了基于数字图像处理技术的盾尾间隙自动测量系统；路亚缇等[8]将超声波传感器安装在盾尾内壁上，建立了盾尾间隙测量系统；孙连等[9]通过对管片位置检测，计算出盾尾间隙；Jin等[10]分析了盾尾间隙的不同，及其对隧道及地面沉降造成的影响；吴恩启等[11]提出了一种有限元与应变相结合的方法，对盾构机的刀盘推力进行实时检测。上述研究大都采用激光及图像等方法进行处理，在测量过程中，若水土杂质覆盖会极大影响测量精度,因此，本文采用在盾尾内部粘贴应变花的方式进行测量。

本文以在温州工地施工的泥水式型盾构机为例，对盾尾变形检测方法进行了研究。

1 盾尾受力分析

盾构机中关键的盾体结构由前盾、中盾和盾尾组成，如图1所示。盾构机在地下施工时，盾尾中的壳体受力主要来自周围的土层压力。理想状况下，左右两侧的土压对称，而下方压力大于上方压力，如图2所示[12]。

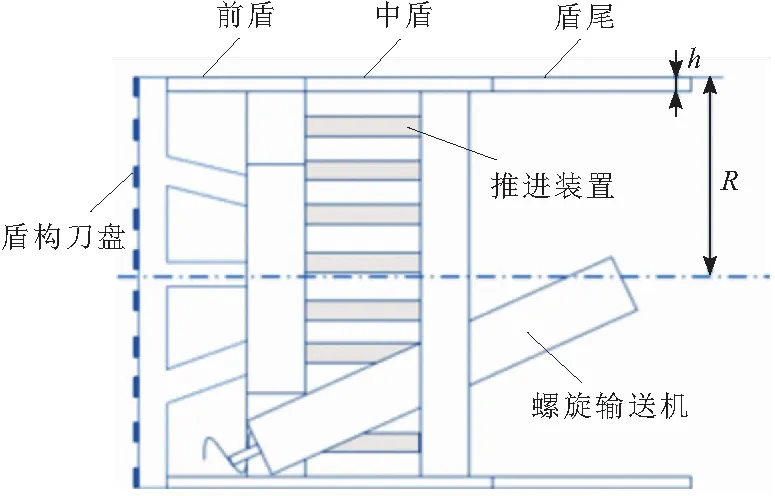
图1 盾构机盾体结构

图2 盾构机受力情况

盾壳压力计算式为

(1)

M0为地面载荷；γ为土的单位体积重量；H为覆土厚度；λ为侧向力系数。

根据盾壳受力分析，可得盾壳圆周上任意一点M的受力为

(2)

qz为径向力；qφ为周向力。该截面受力模型可转化为图3所示。

图3 壳体任意点受力情况

由于盾尾壳体厚度h与盾壳半径R之比远小于1/20，对盾尾的受力分析可按薄壳进行分析，盾尾微元分析如图4所示。

图4 微元分析

假定盾构施工过程中，盾尾壳体的轴向、环向及径向变形量分别为U、V和W，根据柱壳体的基本方程、几何方程及平衡方程可得

(3)

E为弹性模量；v为泊松比。其中轴向变形量U相对于环向、径向变形量较小，可忽略不计。

2 盾尾有限元分析

在模型建立时，保留中盾的支撑及盾尾，忽略一些细小的内部结构，避免计算过程中局部不收敛。同时，为保证仿真结果可靠，模型材料选择与实际壳体材料一致，采用Q345B号钢。简化并施加约束后的盾构模型如图5所示。

图5 盾构模型

盾构深度不同，壳体受周围水土压力的大小也有所差异，假设施工的盾构机位于地下9.24 m，地质类型为淤泥质黏土，则λ取值0.72，地面载荷M0根据实际情况选取，一般取20 kN/m2，各处压力可根据式(1)计算得到，取值如表1所示。

表1 壳体压力取值

对模型施加载荷并进行分析得到应力及变形状况，最大应力为169.67 MPa，内凹最大位移量为15.989 mm，外凸的最大位移量为13.611 mm。

结合有限元分析结果和施工现场空间布置，最终确定选取方便粘贴应变花的12个测点，分别位于盾尾部分的2个截面上，如图6所示。其中，A-A截面与盾尾尾部较近，布置7个测点，B-B截面离盾尾尾部较远，布置5个测点。

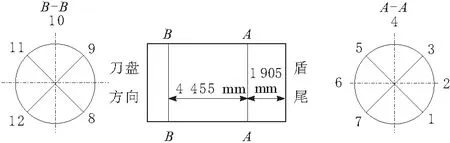
图6 测点位置

将盾构机所受压力按等差数列进行改变，其他条件不变，多次有限元分析后，得到各个测点处应力与变形之间的对应关系，若已知某测点实际应力值，可对应得到该点处的变形值。

3 盾尾变形检测实验

3.1 盾尾变形检测系统

盾尾变形检测系统包括应变花、应变采集仪、交换机和计算机等。检测采用DH3820高速静态应变采集仪，采集频率最高为100 Hz。实验过程中，由于主应力方向未知，因此在应力采集中采用直角45°三相应变花，其尺寸为11.5 mm×11.5 mm，单个应变花占用传感器3个通道，用于确定测点处应变的大小和方向。

在选择的测点处粘贴应变花，应变采集装置与应变花连接，将盾构机在工作时受载荷作用引起的应变量采集起来，经过交换机，最终在电脑上显示。变形检测系统如图7所示。

图7 检测系统

在盾构机进洞之前，先对软件进行调试，并记录此时应变量作为零点值，当盾构机开始工作，盾尾受力之后，采集到的数据减去零点值，得到应变的变化情况。为使数据有足够高的精度，采用0.1 Hz频率，每10 s采集1次，对数据进行滤波处理后取平均值，将此值作为采集到的应变值，通过计算得到等效应力，再结合相应测点的应力变形对应关系，求出盾尾变形。

3.2 应变花的布置

在盾尾内表面进行应变花的粘贴，同时为更好地观察到轴向及其他方向应变变化情况，在粘贴应变花时，一端沿着盾构机轴线方向粘贴，记为0，剩下两端记为45°及90°。现场布置情况如图8所示。

图8 应变花现场布置情况

现场采集应变花应变后，将3个方向的应变记为ε0、ε45和ε90，代入式(4)后，可计算得到应力σ1和σ2,即

(4)

应变花粘贴近似平面，则垂直表面应力σ3=0，测点处等效应力值σ计算式为

(5)

将测点的等效应力对应有限元计算得到的应力与变形的对应关系，根据插值法得出最终的变形量。具体实验流程如图9所示。

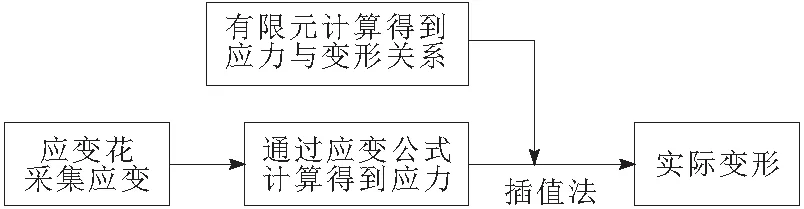
图9 实验流程

3.3 实验过程

本文以温州瓯江口隧道挖掘为工程背景，采用大直径泥水式盾构机，盾壳外径直径为14.87 m，最大覆土厚度为30 m。数据采集从盾构入洞开始至70环结束，并将实验采集到的数据进行整理分析。

4 实验数据分析

4.1 盾构过程中应变状况

盾构未进行推进时，各方向的应变不发生变化，变形也不会改变，如图10前半段示。盾构推进时，盾尾外力改变，应变也会发生相应的变化，如图10后半段所示，3个方向应变情况不同，0方向即轴线方向的应变基本稳定不发生变化，45°及90°方向应变会随外界影响而改变。

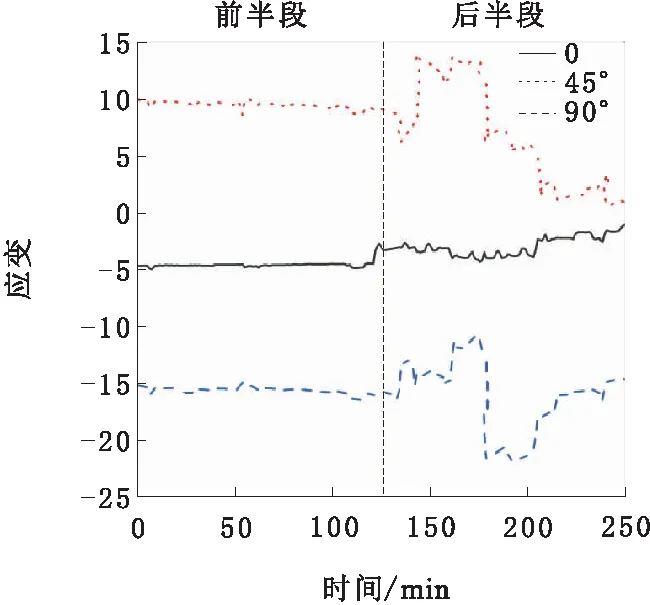
图10 应变状况

4.2 盾构过程中变形情况

盾构进洞之后，受水压土压影响发生变形。将应变采集法得到的变形同有限元及理论的数据进行对比，如图11所示，变形状况三者相吻合，理论值相对较小。其中，在270°位置，容易受到积水影响，未布置测点，采用初始数据代替，因此,实验数据在270°位置小于理论值。

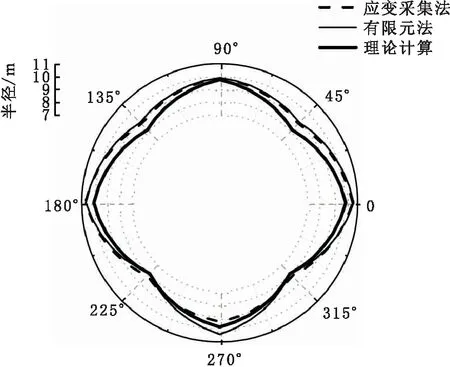
图11 应变采集法同有限元及理论法的对比

越靠近盾尾尾部，与固定端距离越远，变形情况越明显。如表2所示为同一角度，应变采集法不同截面的测点变形量的对比，A截面相比于B截面更靠近盾尾尾部，因此相同角度A截面变形量更大。

表2 不同截面变形量

将盾构过程中51环处应变采集法的数据与现场全站仪的数据进行对比，结果如表3所示。发现两者变形状况大致相似，2种测量方法的差别平均为2.6 mm。其中，测点7差别较大的原因可能为：全站仪进行照射时，此测点位于下半部，可能有杂质覆盖，影响测量结果。

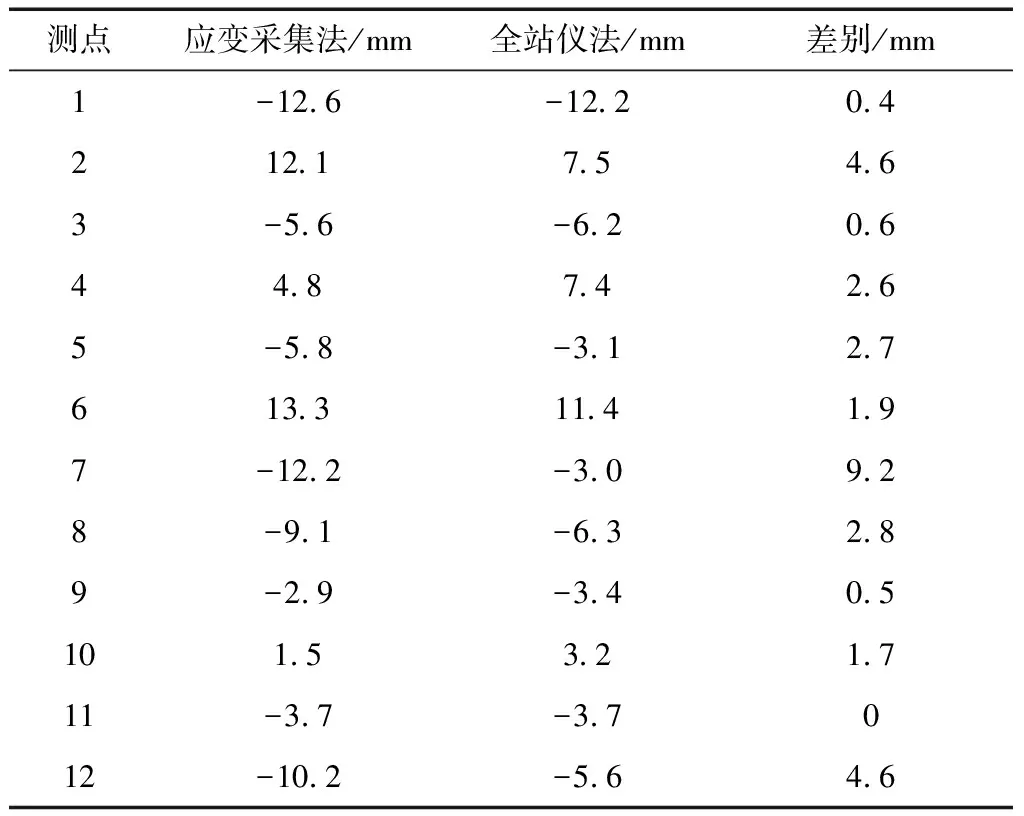
表3 应变采集法与全站仪法的变形量对比

在盾构推进的44～56环，盾构深度未发生太大变化，变形情况基本一致，如图12所示。0方向的测点为最大变形量测点，最大值可达14.35 mm，同时盾尾属于弹性壳体，只要未超过弹性形变，便会随着受力逐渐恢复，如图13所示。

图12 盾尾变形随推进环数的变化

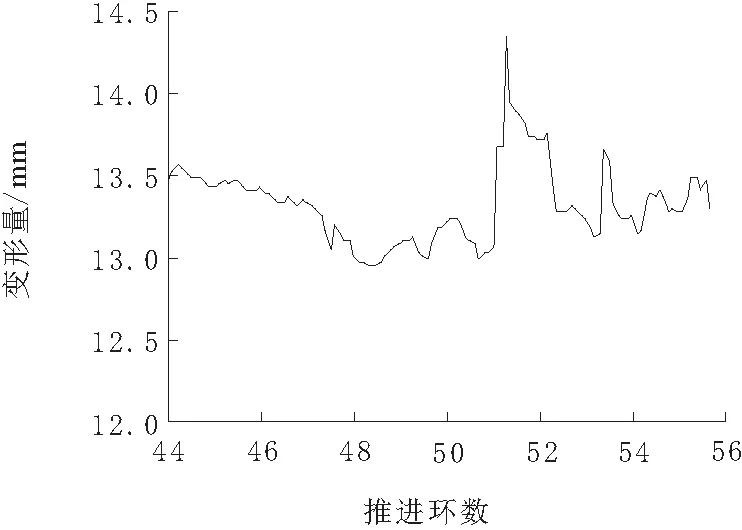
图13 最大变形量变化曲线

5 结束语

盾构机在掘进过程中，实际变形较为复杂。本文提出有限元模型与应变采集相结合的检测方法，同时建立盾尾变形采集系统，实现对盾尾变形的实时采集。对采集到的数据进行分析，并与全站仪数据进行对比，得到以下结论：

a.盾构机壳体变形越靠近盾尾尾部，距离支撑面越远，变形越为明显。

b.本检测方法与全站仪的测试结果相比，具有良好的对应关系，两者的测量差别在工程允许范围内，表明该方法有一定的可行性。

c.盾尾变形属于弹性变形，在掘进过程中，只要未超过弹性形变，则会随着受力而恢复。