基于混合聚类算法的大学生心理健康分析

马晓岩

（中国人民解放军93897 部队保障部卫生队，陕西 西安 710000）

随着社会的发展及教育资源的不断优厚，当今时代大学生越来越多元化，学生的需求也发生了很大变化。大学生的心理健康问题不仅越来越复杂，而且数量越来越多、严重程度也越来越高[1-2]。

为此，许多学者将机器学习用于心理医疗诊断领域[3-4]。杨昱梅[5]等基于数据挖掘理论对大学生心理健康状况进行了分析和研究。杨帆[6]等利用两步聚类和快速聚类两种聚类分析方法对青少年危险行为进行聚类分析，并据此为青少年制订干预方案。聂敏等[7]研究了高校学生心理健康情况对其社交网络结构的影响，挖掘学生的抑郁症状发生水平。Kesuma Z M[8]等利用中值聚类算法对孕产妇心理保健服务进行聚类分析。

上述研究大都采用有监督的机器学习方法来学习模型，其中可以使用标记良好的数据样本。然而，对于心理健康领域存在不足，特别是许多心理健康前期无明显表征，或者其特征是不确定或短暂的状态。因此，在该文研究中，假设在那些有极端心理健康问题与正常健康状态之间存在一些中间阶段，并提出了K-means 结合蚁狮优化算法对学生进行聚类划分，进一步帮助了解大学生心理健康阶段，为大学生心理辅导或心理干预提供参考。

1 相关概念

1.1 K-means聚类分析算法

聚类[9-11]是基于某种相似性度量对一组对象进行分组的过程。每一组分区对象都称为一个集群。分区是通过聚类算法来完成的。因此，聚类是有利的，因为它可以在相同的数据中获得先前未知的组。数据聚类是发现数据集中结构的有效方法。一些聚类方法将对象划分为簇之间没有特定的边界，而其他一些方法则将对象划分为互斥的簇。同时，也有一些方法把两个物体之间的距离作为相似度的标准。

K-means 聚类[12-13]是一种无监督的硬划分聚类方法。目标是目标函数J，从数据中找到k个聚类，具体定义如下：

其中，d2(Ci-Xj)是第i个簇质心和第j个数据点之间的欧式距离的平方。N是数据点的总数。根据得到的距离，将点分配给距离质心最小的簇。在对这些点进行聚类后，找到属于该聚类的所有点的平均值。然后将平均值指定为下一次迭代的新的聚类质心。重复这个过程，直到得到的质心与上一次迭代的质心相同。K-means 算法的目标是最小化目标函数。

1.2 蚁狮优化模型

蚁狮优化模型[14-15]是一种自然启发的算法，它遵循蚂蚁幼虫的捕食行为。一只蚁狮幼虫在沙子里沿着一条环形的路径移动，用它巨大的颚把沙子扔出去，从而形成一个圆锥形的洞。挖完陷阱后，幼虫躲在圆锥体的底部，等待蚂蚁被困在坑里。一旦蚁狮意识到猎物被困住了，它就会把沙子向外扔，并把猎物滑进坑里。当猎物被抓进下巴时，蚁狮会把猎物拉向自己并吃掉。这个过程在数学上被设计用来执行优化。该方法主要有5 个步骤如下：

1）蚂蚁的随机游动；

2）建立陷阱；

3）将蚂蚁困在陷阱中；

4）捕捉猎物；

5）重建陷阱。

蚂蚁利用随机游动在受蚂蚁陷阱影响的搜索空间中移动。在每次迭代中，蚂蚁的位置都会随着随机游动而更新。迭代t的随机游动由如下公式获取：

其中，X(t) 为蚂蚁随机游动时步数的集合。cussum为计算过程中的累加和。t为迭代过程中的步长，r(t)为随机函数，具体定义如下：

为了确保所有随机游动都在搜索空间的边界内，使用如下所示的归一化公式：

其中，ai、bi分别为第i维变量随机游动的最大值和最小值。分别为第i维变量在迭代t时的最小值和最大值。

此外，蚂蚁制造的陷阱将会对其随机行走产生影响，为此建立如下模型：

其中，ct、dt分别为所有变量的最小值和最大值，为第j只蚂蚁在迭代t时的位置。

进一步采用轮盘赌选择方法，根据蚂蚁的适应度值进行优化。在每次迭代中将最适合的蚂蚁保存为精英蚂蚁。精英将影响蚂蚁的整体运动。此外，蚂蚁的位置会根据所选蚂蚁和精英的随机游动来更新。每只蚂蚁都会绕着一只选定的蚂蚁游走，因此也可能会围绕精英游走。该过程可描述为：

其中，为蚂蚁利用轮盘赌在迭代值为t时到蚁狮周围随机游动l步时的值。为蚂蚁在迭代t时到精英蚁狮周围随机游动l步时的值。

此外，计算所有蚂蚁的适应值。如果一只蚂蚁比剩余蚂蚁有更好的适应能力，则其被相应的蚂蚁取代。同样地，如果任何一个蚁狮比精英蚁狮更优，则精英蚁狮也会被该蚁狮取代。

2 改进的混合聚类分析算法

该节将介绍一种改进的混合聚类分析算法，为帮助了解大学生心理健康阶段，为大学生心理辅导或心理干预提供参考。该算法是由K-means 和蚁狮优化算法混合而成。

2.1 算法执行过程

首先，确定要形成的簇的数目。然后根据得到的最小欧氏距离对所有数据点进行聚类。然后，为得到的每个簇计算优化的簇质心。在优化过程中，每个簇随机初始化为蚂蚁和蚂蚁种群。然后利用K-means 聚类方法的目标函数，计算所有蚂蚁和蚂蚁的适应度值。当簇内距离的平均值之和最小时，将适应度值最小的蚁群作为精英值。之后对每一个簇进行蚁狮优化，得到簇质心的最佳位置。K-means聚类算法将返回的精英作为质心。该方法的流程如图1 所示。

图1 改进的混合聚类分析算法执行流程

2.2 算法性能指标

为验证算法性能，基于不同的性能指标对算法的聚类质量进行了评价。文中引入的性能指标是群内距离平均值和F测度。

2.2.1 群内平均距离

聚类的原则是属于同一簇的数据点应尽可能靠近，即簇内距离应尽可能小，以获得最优的聚类质量。

常用计算簇内距离[16]的方法有欧式距离d、曼哈顿距离d12和余弦相似度dc等，距离计算公式如下：

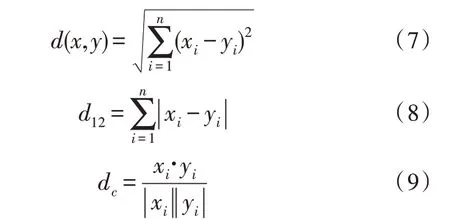
其中，xi、yi为簇内任意两个点的值，n为簇内点的数目。

2.2.2 F测度

利用信息检索[17]中准确率和召回率的概念计算F测度。数据集的每个聚类i记为查询所需的ni项集，每个聚类j记为一个查询检索到的一组nj项。故nij表示聚类j中第i类的元素数量。因此，准确度pre、召回率re和F测度的计算公式如下：

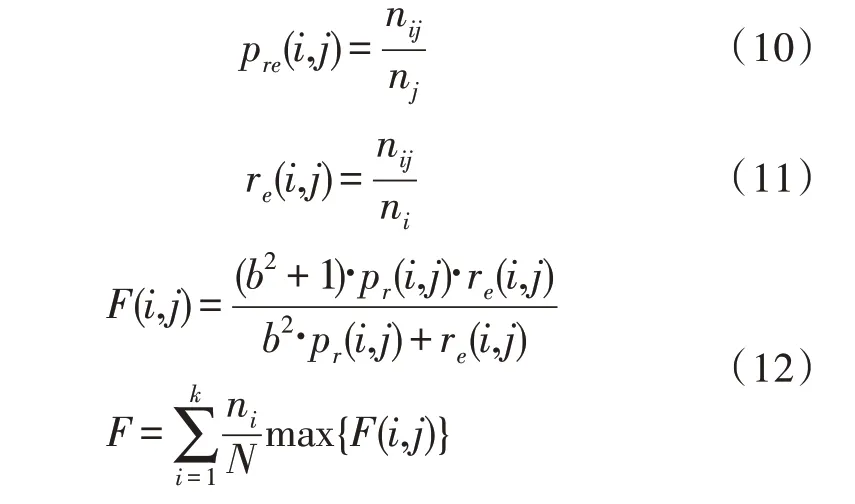
3 实验分析

为分析大学生的压力和健康相关行为，以一个实际案例验证所提方法。首先，数据集由问卷调查方式通过统计参与者在近两个月内的情况生成，每个问题分为有1～5 分5 个等级。表1 所示为调查结果部分统计情况。

表1 部分心理测试试题

3.1 算法性能测试

利用文中所提方法对数据集进行聚类分析。图2 所示为578 名学生心理健康聚类结果，其中横轴表示聚类划分的不同层级，包括正常、轻微、中等、严重和特别严重5 个级别。可以看出调查结果中49.6%的人有轻度或更高的抑郁症状，60.0%的人有焦虑症状，42.0%的人有精神压力。

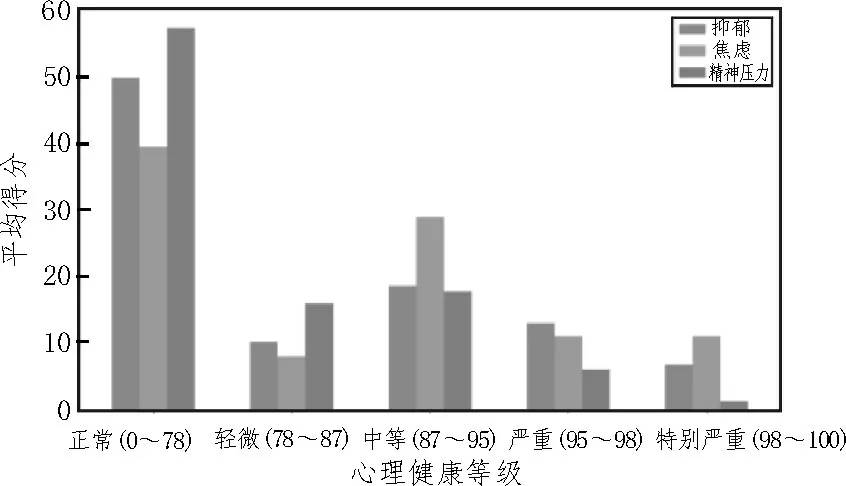
图2 心理健康聚类结果

将文中算法的聚类结果归一化后与传统K-means、K-means PSO、K-means FA、模糊K-means 相比，聚类结果的群内平均距离和F测度如表2 所示。可以看出，K-means PSO 和文中方法提供了最小的簇内距离。随着迭代次数的增加，模糊K-means 和文中算法比较稳定不会出现波动现象。综合比较，文中方法比其他方法结果更好。

表2 不同算法性能对比结果

3.2 算法差异性测试

为了确定聚类算法之间是否存在显著的性能差异，将测试者分为4 组进行统计分析。为了确定差异，文中采用了Friedman 检验[18]。Friedman 检验是一种非参数检验，用于找出顺序因变量组间的差异。零假设用H0描述所有聚类算法的性能相同。

试验的置信水平α取0.1。对于每组数据，所有算法都进行了相应的排序计算，故j个算法的平均排序Rj计算如下：

其中，N为测试次数，为第j个算法在第i（i∈[1,N]）次测试中的排序。表3 所示为不同算法在测试中的排序统计结果。可以看出文中方法表现最好，K-means 方法表现最差。

表3 不同算法排序统计结果

Friedman 检验计算公式如下：

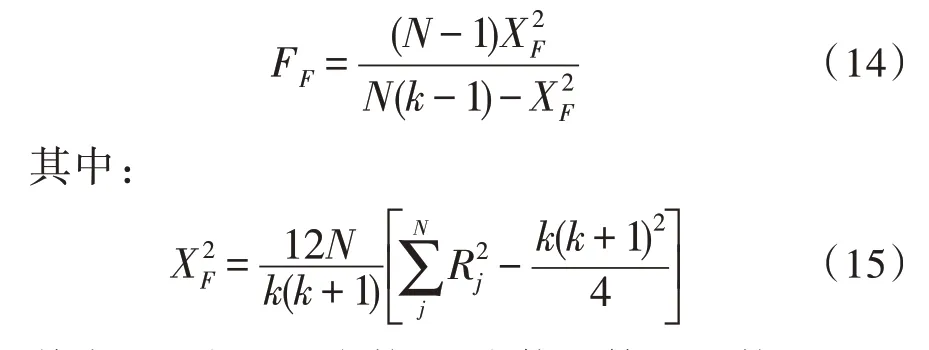
其中，N为测试次数；k为使用算法的数量。

Friedman 统计量FF由自由度为k-1 和(k-1)(N-1)的F分布构成。对于5 个算法和8 个数据集，自由度在4～28 之间。Friedman 检验中z值计算公式如下：

然后，利用z值得到概率p与α/(k-1)。表4 为不同算法的Friedman 检验统计结果。

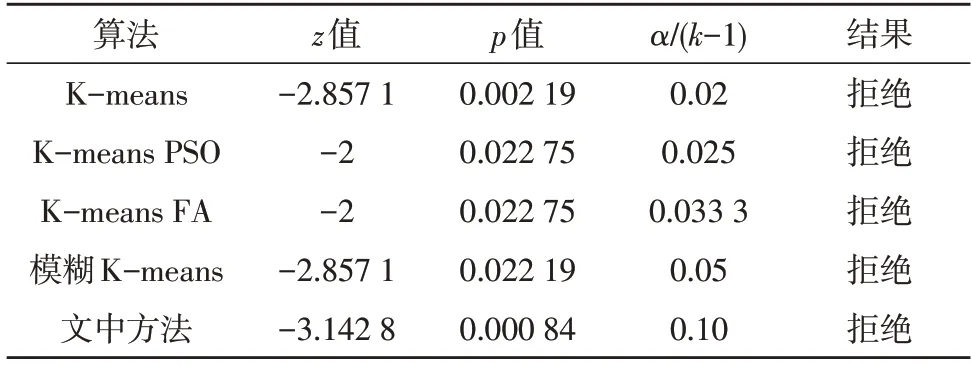
表4 Friedman检验统计结果

由表4 可知，无效假设被拒绝。因此各算法性能不同。综合以上分析结果，可以确定文中所提方法在统计上比K-means、K-means PSO、K-means FA、模糊K-means 算法表现更好。

4 结论

文中对大学生心理健康的聚类分析问题进行了研究，提出了应用于大学生心理健康程度的聚类分析模型，并实现了一种混合聚类优化算法。

文中在模型验证时选取的数据类型较为基础，仍存在进一步提升空间。同时对数据整合时仅为统计学分析，没有进行数据挖掘与内部关系探讨。未来研究的方向包括数据校验，挖掘各指标之间内涵关系等。