一种改进的四旋翼飞行器自适应姿态融合算法

高怡，李东航

（西安石油大学电子工程学院，陕西 西安 710065）

四旋翼飞行器(quadrotor)具有体积小、机动性强、隐蔽性好、安全性高等优点，目前被广泛应用于农业、军事、新闻等领域[1]。姿态航向参考系统(AHRS)是一种基于微机电系统(MEMS)的高性能、低成本捷联式惯性导航测量装置[2]，目前成为了四旋翼飞行器的主要惯性测量传感器[3]。四旋翼飞行器姿态解算工作的速率与精度直接影响了其飞行的质量，所以设计出更加快速、精确的数据融合与姿态解算算法成为当前研究的热点之一。

文献[4]首次将梯度下降法(Gradient Descent,GD)应用在了飞行器姿态解算领域中。但为满足四旋翼飞行器越来越高精度的姿态测量要求，不少学者又基于此算法提出了多种改进算法。文献[5]将步长与飞行器的角速度关联起来构成了动态步长。文献[6]根据运动加速度值及加速度增量的变化得到自适应因子，从而提高了系统在运动状态中的稳定性。文献[7]将融合前的两传感器数据进行互补滤波，根据角速度和加速度大小自适应调整β参数，但该方法较为繁琐，收敛速度较慢。文献[8-9]引入动量以改进每次迭代的优化方向，提高了梯度下降收敛速度和精度，但精确的动量数据不易获得。

该文以梯度下降法为基础，提出一种变步长的自适应姿态融合算法——当设备在一段时间内的运动加速度数学期望值越大时，算法自适应地对加速度计的信任程度降低，即使梯度下降的补偿成分降低，从而提高解算的精度。

1 飞行器姿态描述

1.1 坐标系与姿态角

选用地理坐标系东、北、天(O-ENU)作为参考坐标系(Reference Coordinate System)，坐标原点位于载体重心。载体坐标系(Carrier Coordinate System)X轴为机体平面向右方向，与机体轴线垂直，Y轴为机头所对正前方方向，Z轴垂直于XOY平面向上，构成坐标系O-XYZ。载体坐标系与地理坐标系如图1 所示，机体绕X轴旋转产生俯仰角(Pitch)，绕Y轴旋转产生滚转角(Roll)，绕Z轴旋转产生偏航角(Yaw)，分别用欧拉角θ、φ、ψ表示[10]。

图1 载体坐标系与地理坐标系

1.2 四元数法姿态求解

四元数最早于19 世纪被提出，并建立了相关的数学理论。20 世纪中叶以来，随着计算机的发明以及航天技术的发展，四元数才得到人们的重视[11]。

捷联惯性导航系统中定义四元数Λ 为：

其中，i2=j2=k2=ijk=-1。

四元数微分方程定义如下[12]：

可采用离散方法求解四元数微分方程：若系统采样周期为Ts，离散后的方程[13]为：

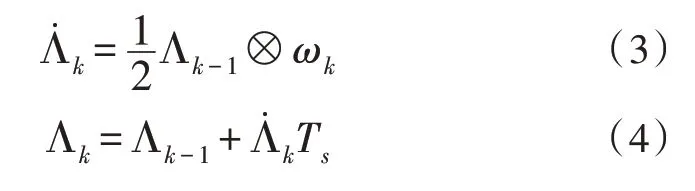
由四元数旋转矩阵可解得3 个姿态角：

设初始四元数Λ0=[1 0 0 0]T，首先由式（3）、（4）可得到t时刻的四元数Λk，代入式（5）即可求得t时刻的3 个姿态角θ、φ、ψ。

2 传感器数据融合与姿态解算

2.1 经典梯度下降算法姿态融合

梯度下降公式[14]为：

其中，∇F(xn)为梯度值，μt为收敛步长。

假设目标姿态为λ∇,t，由梯度下降法有：

设基于陀螺仪微分方程求解到的姿态为λω,t，则融合姿态为[15]：

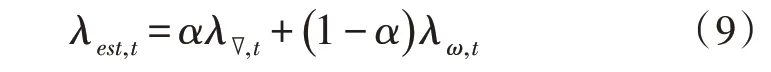
其中，0 ≤α≤1。

由于α的值很大，取式（8）的近似值并将所有表达式代入式（9），可得最终融合算法公式为[7]：

其中，β为λω,t的收敛速率，由手册查到。

磁力计和加速度计的数据融合与上述过程类似，不再赘述。

2.2 自适应变步长姿态融合

当飞行器处于运动状态时，重力场的测量值会存在偏差，所以需要减少梯度下降的补偿量从而减少对加速度计的信任程度[16]。换句话说，公式中需要引入一个可变因子，在运动加速度越大时使β值越小。

设加速度的实际测量值为a，重力加速度用g表示，运动加速度即为二者之差。t时刻的前n个采样点的运动加速度数学期望值为En，引入自适应因子ρa与常数控制因子Cona，则有：

融合公式（10）也发生改变，如式（12）所示：

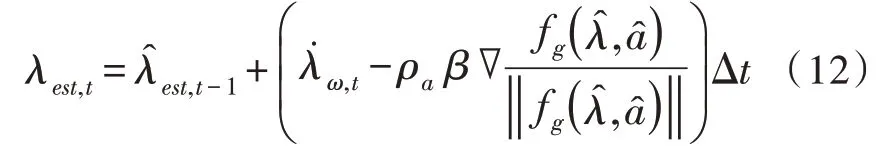
当四旋翼飞行器高速飞行时，可通过常数控制因子使自适应因子与期望值呈负相关。据此原理，算法可以自适应地控制补偿量的变化：运动加速度数据的数学期望越大，梯度下降部分的补偿成分越小。在实际应用中，可以通过调节常数控制因子Cona与采样点数n，来减少高频干扰，进而提高系统的稳定性。

自适应算法简明流程图如图2 所示。

图2 自适应算法简明流程图

3 实验与分析

3.1 实验平台

实验使用AHRS模块搭建测试平台，该AHRS模块主控制芯片采用STM32F103T8，ARM 32-bit Cortex™-M3 内核，模块传感器部分组合使用了MPU6050 传感器(其中包括加速度计、陀螺仪各一个)、HMC5883L传感器(包括HMC118X 系列磁阻传感器和相关集成电路)以及一个气压高度计BMP180，AHRS 模块如图3 所示，模块实际尺寸为37.2 mm×21.4 mm。

图3 AHRS模块

AHRS 模块与PC 通过USB-TTL 转换模块(以CP2102 为内核)连接，用于实现AHRS 设备的供电与通信，该转换模块如图4 所示。串口所连接的PC 软件可直接读取和导出各传感器数据，并给出设备的实时理论准确姿态曲线。

图4 USB-TTL转换模块

测试平台具有三轴旋转维度，可模拟四旋翼飞行器在空间中的各种运动姿态。

3.2 实验结果

为了验证该算法的可靠性，选择ψ角作为验证角。实验中，设定实验平台的轨迹为绕Z轴由0°旋转至90°再旋转至-90°，通过上位机软件导出两传感器的数据并储存。两传感器采集的数据如图5(a)、(b)所示，其三轴分量以不同线型进行区分。

对自适应算法(AGD) 编程，各参数经调试后设置如下：采样间隔T=1/256 s、融合步长β=0.1、常数控制因子Cona=0.95。实验以互补滤波算法(CF)、经典梯度下降算法(GD)为对照组，将导出的传感器数据分别读入3 个算法程序进行解算，各算法对于同一轨迹的传感器数据偏航角ψ的解算结果如图5(c)、(d)所示。图5 (c)中，实线为设备偏航角的理论精确姿态，从图中可以大致看出，3 种算法均成功解算出了设备的姿态。图5(d)为4～6 s 解算结果的局部放大图，可以直观比较3 种算法的解算效果。

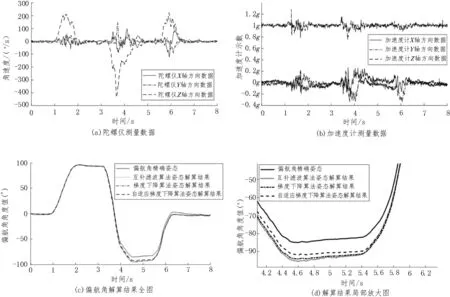
图5 算法测试图

由表1 解算结果误差数值比较可以看出，3 种算法的误差平均值均在3°左右，这是由于该算法只进行基于运动加速度的变步长研究，未包含磁力计和气压高度计的补偿。在标准差方面，CF 方法下的误差波动较大，GD 算法次之，AGD 算法结果最为稳定；在平均值方面，就该实验而言，AGD 算法的精度较其他两种算法分别提高了0.557°和0.708°。

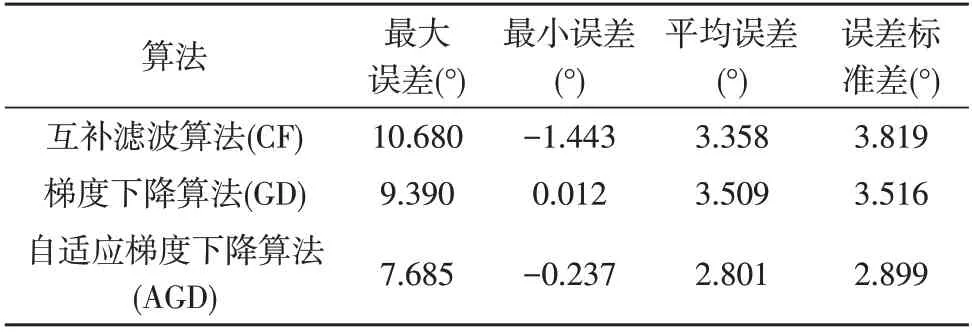
表1 解算结果误差比较

4 结论

在四旋翼飞行器姿态测量中，高速且精确的姿态解算对飞行器控制有着至关重要的作用。该文提出了一种基于梯度下降的自适应变步长姿态融合算法，该算法可根据运动加速度的大小调整对加速度计数据的信任程度，从而提高解算精度。实验中，该算法在解算AHRS 设备的偏航角时，收敛速度快，姿态输出平稳，解算精度得到明显提高。因此，该算法有较好的研究参考与工程应用价值。