基于深度神经网络的异常财务数据识别方法
冯华伟
(河南省太康县人民医院,河南 周口 461400)
作为医院财务系统的重要组成部分,医疗账务支付系统承担着医院财务结算的重要任务,也是维持医院正常运转的关键。同时,支付系统也存在着较高的安全风险,例如信用卡套现、医疗保险诈骗以及账目作假等。这些财务数据的造假行为严重影响了医院财务系统的正常运转,同时也影响了医院以及社会的公共利益。而根据国外机构的调查,近年来通过金融诈骗而构成的财务系统损失可能超过机构年收入的5%[1-2]。因此,对财务异常数据的准确识别是保障财务系统正常运转的重要途径。
近年来,随着医院财务数据数字化进程的逐步加快,财务数据的整体特点也转变为数据量巨大、数据增长速度快、数据类型复杂化等。传统检测方法使用数学的统计方法进行验证,其优点是可以直观快速地筛选出异常数据,但缺点是无法处理海量数据[3]。同时,传统检测方法也无法满足当前的复杂检测需求。而深度学习的出现引起了学者的广泛关注[4],文中融合了随机森林算法与神经网络技术,提出了一种改进的异常数据检测方法,并改善了当前算法中存在的复杂度较高、检测误差大以及检测效率低等问题。
1 异常数据检测模型
1.1 财务数据特征说明
对财务数据的两个特征[5-6]作如下说明:
1)信息熵
信息熵是数据处理领域常见的衡量标准,该指标可用来判定数据样本的不确定性。信息熵越大,代表样本的确定性越小;信息熵越小,代表样本的确定性越大。
信息熵计算公式如下:
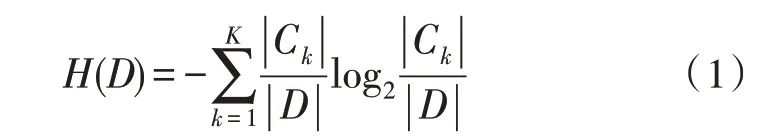
式(1)中,D为样本数据集,Ck为k属性样本。在这些样本中,C0为异常类型的样本,C1是正常类型的样本。
2)信息增益率
信息增益率通常用来表示金融样本数据的一种分类标准,即对于数据集合的属性特征部分,可定义为:
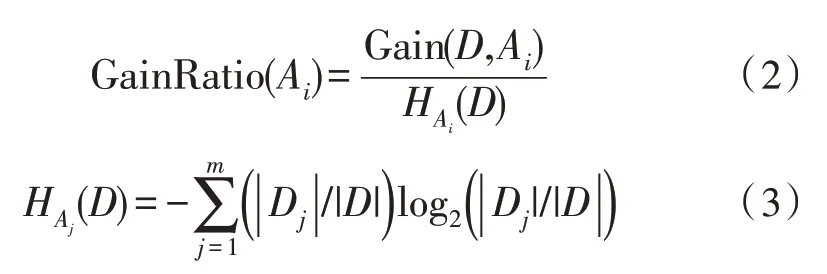
金融数据还有时间特征,因此在对金融数据进行分析时还需考虑其时间特征。故此,结合时间特征的异常数据增益可定义为:
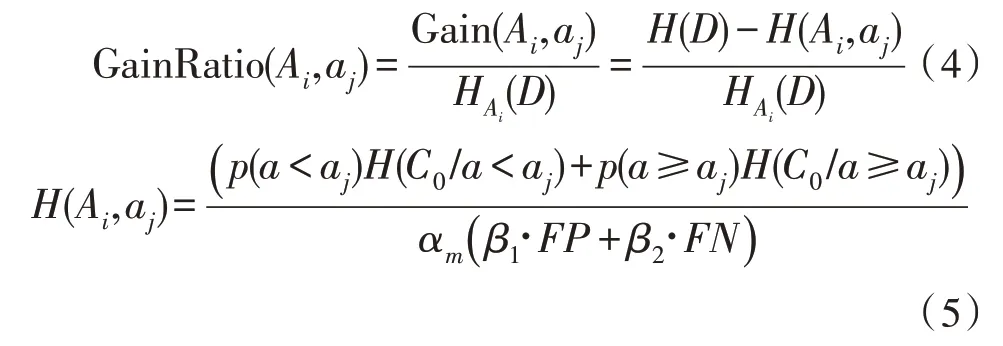
式(5)中,Ai为异常数据的特征信息,αm为时间影响因子,该参数用来表征过去数据对当前数据的影响。αm可以表示为:
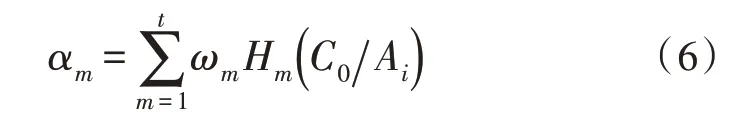
式(6)中,ωm为第m个时刻的权重因子,Hm表示异常数据类别划分因子。该因子越小,即对数据类别的划分越有利。
1.2 随机森林算法
随机森林算法[7-9]的本质是多项目决策算法,该算法最初是在二值树算法基础上进行改进的。其特征为算法样本集合中的异常数据集合即稀疏矩阵集合,同时也是一种无监督的单一数据监测方法。随机森林算法使用二值树算法结构,将数据子集的每一个数据均作为二值树中的节点。
该算法所需的数据不需要过多异常点,但同时异常点需要满足数据特征与其他正常数据点以及数据特征隔离量较大的条件,算法才能建立多个森林树。并通过随机特征选取不同的分割点特征,进而构建完整的森林树结构。随机森林算法流程如图1所示。
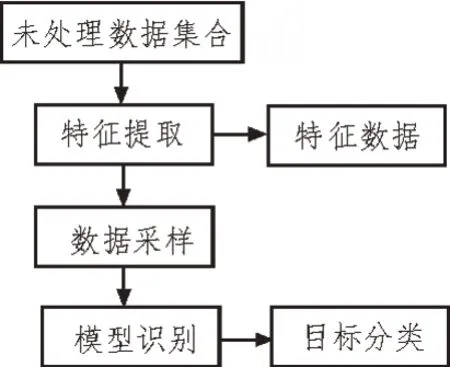
图1 随机森林算法流程
需要指出的是,文中森林树的构建所需采集样本无需过多,数据的异常构建公式如下:
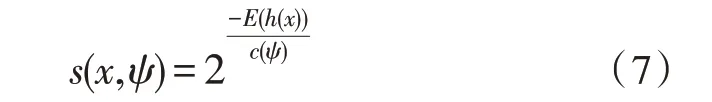
式(7)中,c(Ψ)是在数据采集量为Ψ的情况下,构建的二值树无法进行搜索的总路径长度。当路径长度较长时,该参数值趋近于0;当路径长度和c(Ψ)值大体相当时,该参数值趋近于0.5;当路径长度为零时,该参数值趋近于1。但这种传统森林算法,无法解决大量异常数据同时聚类的情况。
文中对随机森林进行了改进,构建了方差随机森林算法,并向随机森林算法中加入方差特征值。这样随机森林算法可进行更优的聚类分析,算法构造函数如式(8)所示:
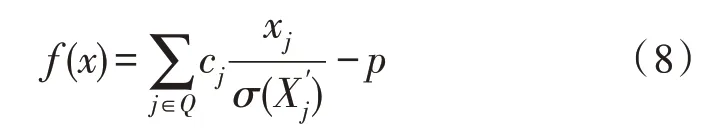
式中,样本特征集合为Q,cj为随机系数,p为截距。截距表达方程如式(9)所示:
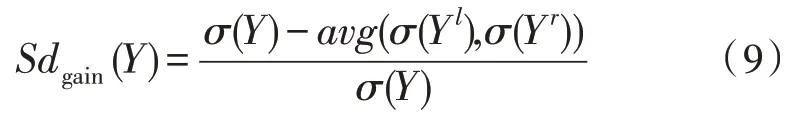
该改进算法在计算树的路径长度时,使用cj系数进行判断,这样可以使得p截距取最大值。
1.3 深度神经网络异常数据监测模型
构建深度神经网络模型对随机森林算法数据进行训练。文中使用RNN 网络结构进行训练[10-12],RNN 为循环卷积神经网络,该网络的模型示意图如图2 所示。
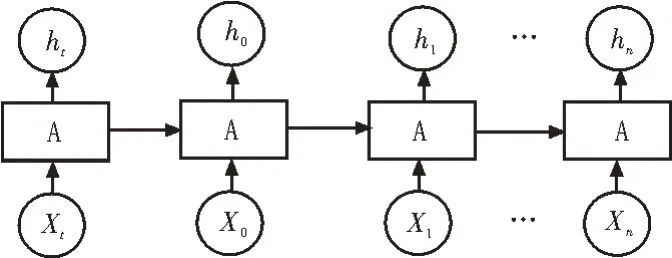
图2 RNN模型示意图
RNN 网络单元的主要用途为序列数据的训练与处理。该神经网络的特点是每个单元的输出层均可返回至输入层作循环卷积。这种结构适合于时间结构,对随机森林算法尤为适用,可有效地减少数据的训练次数。文中神经网络的损失函数L和梯度参数U的关系为:

文中算法的流程如图3 所示。首先对样本数据集合进行随机森林算法验证,这样即可以对每一个异常值进行聚类和分析。然后根据预处理的数据对异常数据样本进行筛选,将筛选完成的结果输入至RNN 网络中进行特征训练。
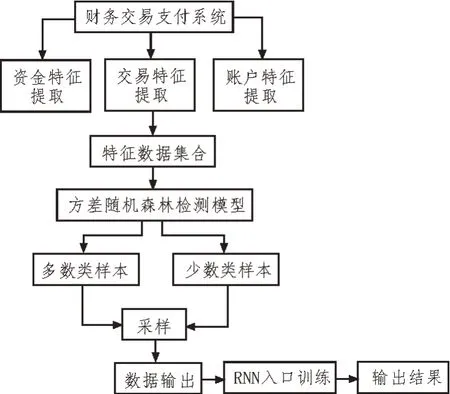
图3 文中算法流程
具体的实现过程如下:
1)通过方差随机森林算法对样本数据集进行异常数据检测,同时对异常数据进行标记,得到标记子集为:
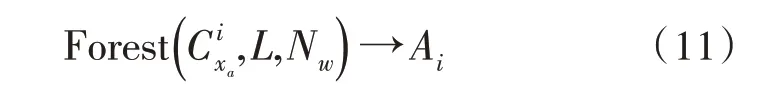
2)将异常数据子集Ai加入到异常样本数据集合中,剩下的数据子集加入到正常样本数据集合中,然后进行筛选,并将其加载至RNN 的入口。
模型实现过程的伪代码如下:
Input:Forestree(D,h,emax),Forestree 为文中森林算法,h为森林树的高度,hmax为森林树的最大高度。
Output:子树的数据集合。
1)Start;
2)设置hmax的值,大小为子采样的对数;
3)ifh≥emax&D≤1 then;
4)return 前个树节点;
5)else 对于任何的属性样本,计算当前时间序列的时间影响因子αm,然后计算信息增益比值,该值求得的最大值即为当前森林树的分裂值;
6)D→filter(D),将筛选后的子集合传递至结果处;
7)返回节点;
8)end if。
1.4 数据检测指标
随机森林检测系统是分类系统,因此文中使用分类效果参数对分类系统的效果进行评估。典型的参数值有准确率、召回率、F1 值[13-16]。
准确率一般是针对异常数据的评价标准,文中指算法可以成功识别异常数据的概率值,其计算公式为:
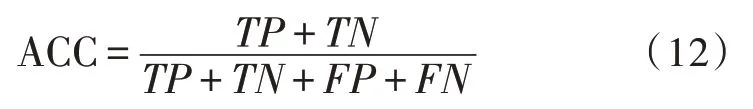
召回率的计算公式为:

F1 值综合了准确率以及召回率,计算公式如下所示:

与此同时,为了直观地观测到分类特征,还运用了ROC 曲线进行验证。该曲线的X轴坐标为假正率FPR,Y轴坐标为假负率TPR,该曲线值通常用来判断二分类器性能的重要指标。与ROC 曲线关联的还有AUC 值,该值用来表征ROC 曲线下方和坐标轴形成的面积大小。该面积可定量对模型的性能进行评估说明,AUC 值越大说明算法性能越优。
2 实证分析
2.1 实验数据以及实验环境
文中数据使用两个训练样本集和一个测试样本集进行实验。训练样本集的来源为某调查机构提供的资金交易数据,交易数据集合属性为交易账户信息、交易金额以及交易方向等金融属性。最终训练结果指向交易账户,将训练测得的交易账户异常数据和真实的交易账户异常数据进行比较,进而对模型的算法准确性进行验证。
训练数据集共有数据样本15 000 个,测试样本集合为5 000 个,实验数据环境配置如表1 所示。

表1 数据环境配置
2.2 实验数据预处理
由于样本数据集存在着属性缺失或属性造假的情况,因此需要对实验数据进行预处理。其预处理步骤为:
1)数据筛选
首先对原始数据的属性不完整数据进行清除,然后对造假的数据进行清除。例如,该数据中存在金融开户户主和银行卡卡主姓名不一致的情况,删除此类数据。
2)数据特征分类
数据的属性有交易账户信息、交易金额以及交易方向等,按照数据特征进行数据分类。
3)数据归一化
将数据的分类值转换成特征值,将数据均做成长度相同的归一化数据,便于算法的训练。
2.3 实验设计以及结果分析
为了验证文中算法检测异常数据的性能进行对比实验。文中使用多个对比算法对测试数据集合进行处理,对比算法处理后的准确率、召回率以及F1值指标。文中使用随机特征选择算法(Ram)、基本随机森林(Forest)算法、ADA 同步算法(ADAsync)3种对比算法,表2 为对比实验指标结果。
由表2 可看出,文中算法的综合F1 值是最高的。虽然随机特征选择算法的召回率较高,但准确率较低。这是因为该算法在进行样本处理时,会有跨文本处理的风险,因此并不适用于金融数据处理。而文中算法具有更优的特征选择能力,可有效地提升分类器的分类性能,算法的F1 值相较其他算法均有2%以上的提升。
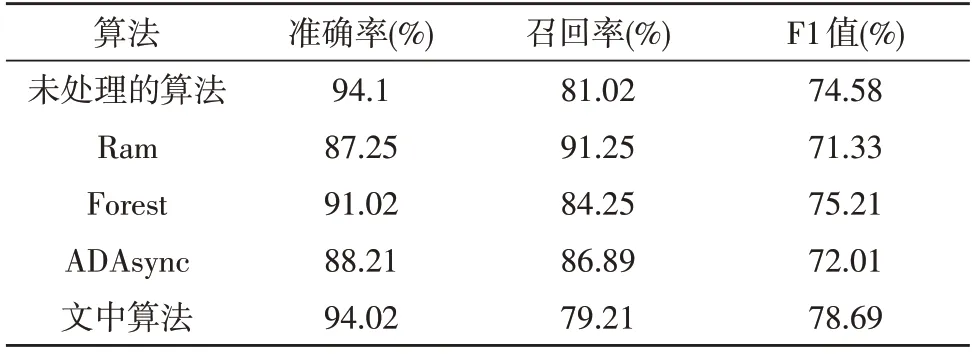
表2 实验结果
ROC 曲线可以对分类特征进行直观地检测,使用统计软件对文中算法处理结果进行ROC 曲线的绘制,曲线如图4 所示。
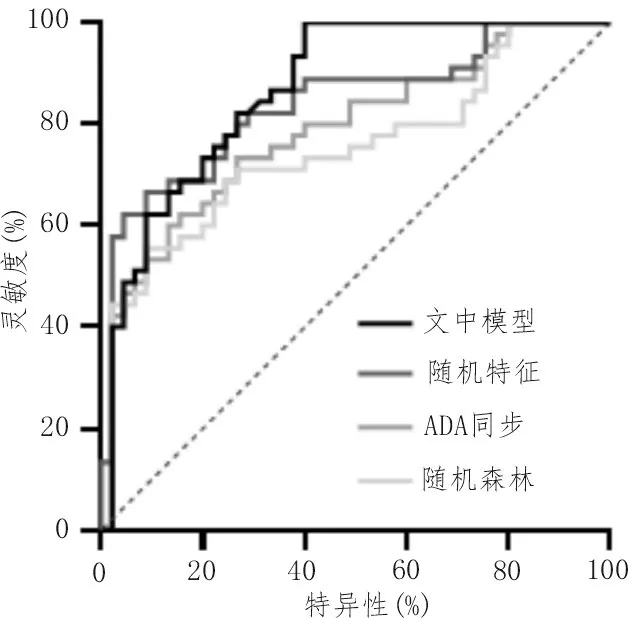
图4 算法的ROC曲线
由图4 可以定性的看出,各个算法的分类性能大体相当,文中算法相较其他算法有所提升。而为了定量的判断算法的分类性能,对AUC 值进行了估算,AUC 值计算结果如表3 所示。

表3 AUC值计算结果
从AUC 计算结果可知,文中算法的AUC 值最高。表明文中算法对金融异常数据的检测有良好的效果。
3 结束语
传统检测方法无法用来检测当前海量的财务数据。文中提出了基于深度神经网络的异常数据检测方法,有效改善了当前算法中存在的复杂度较高、检测误差大以及检测效率低等问题。实验结果表明,文中算法F1 值以及AUC 值相较其他算法均有不同程度的提升,表明该算法对财务异常数据的检测有较为理想的效果。

