大型立式轴流泵运行安全可靠性分析及改造

张 宇， 李 扬， 仇建春

(1. 江苏省太湖地区水利工程管理处， 江苏 苏州 215128； 2. 江苏省江都水利工程管理处， 江苏 扬州 225200； 3. 扬州大学 水利科学与工程学院， 江苏 扬州 225009； 4. 河海大学 水资源高效利用与工程安全国家工程研究中心， 南京 210098)

江都水利枢纽是国家南水北调东线工程的源头工程，以四座大型电力抽水站为核心，江都第四抽水站(江都四站)是其中规模最大的泵站，采用大型立式轴流泵，兼具流量大、可靠性高和运行维护方便等优点，发挥着调水、排涝、通航和发电等综合效益[1-2].江都四站的安全有效运行关系重大，经过长期运行在机组大修时发现，叶轮外壳铸铁件部分气蚀严重，镶嵌不锈钢开裂，叶轮密封漏油等故障，经过维修处理解决了已发生的故障.为避免轴流泵故障频发，需要对其进行可靠性验证，而力学特性分析是评价结构安全的重要途径.关于轴流泵的力学性态研究，其结构内部湍流流态特征分析尤其重要[3-5].轴流泵内部流态十分复杂，一般为三维非稳定湍流，并可能伴随分离、二次流、气蚀、叶尖泄漏等流动现象[6].严重时，非稳定流态还会引发机组振动，并导致轴承磨损、泵站效率降低、缩短机组的零部件寿命等问题[7-8].因此，如何准确地模拟和分析轴流泵内部湍流流态特征，并根据流态数值模拟结果对轴流泵进行力学特性分析，对指导轴流泵的安全有效运行具有重要意义.在研究和分析轴流泵内部湍流流态特征方面，国内学者已取得一定的研究进展[9-13].但是，不少关于轴流泵流态的模拟研究忽略了分子粘性系数的影响，这种假定在模拟离开壁面一定距离的高雷诺数(Re)流态区域适用.但是，在与壁面相邻近的低雷诺数区域，分子粘性系数影响相应较大，不容忽视.

本文采用壁面函数法模拟壁面附近区域的流动，基于对数分布律对壁面附近低雷诺数区有效扩散系数和k、ε边界条件进行了定义，采用有限差分法对低雷诺数湍流模型进行求解，并对轴流泵的湍流流态和轴流泵受力特性进行了数值分析.在此流态模拟分析结果基础上，结合三维空间有限元数值模拟技术，采用材料力学中提到的第四强度理论，对轴流泵进行刚强度校核分析.通过对轴流泵调节拉杆和叶片表面进行受力分析，结合轴流泵的流态模拟分析结果，对拉杆的调节力和驱动力进行了求解.以江都四站轴流泵为研究对象，将所提方法用于三种工况下该结构的力学性态研究和分析，验证了江都四站轴流泵力学性态的安全性.经过排查分析，叶片、调节机构拐臂受力均在正常范围内，而液压站外置、叶片调节机构系统结构复杂、管路接头多等造成渗漏油等故障频发.

1 立式轴流泵故障分析处理

1.1 叶轮外壳气蚀故障与分析处理

江都四站2008年进行主机组更新改造后共安装7台2900ZLQ30-7.8型轴流泵，配套TL3400—40/3400同步电动机，总装机容量23 800 kW，设计流量210 m3/s，泵站设计扬程7.8 m.2016年在运行中发现1号主水泵叶轮发生金属碰擦音，停机后开展水导检查，发现叶轮外壳内嵌不锈钢出现裂缝，垂直方向长度约为7 cm，水平方向约为1 m，如图1所示.不锈钢下方空鼓，不锈钢上下两侧铸铁件部分产生大量的气蚀坑，经分析主要由于叶轮在运行中产生气蚀，首先破坏了铸铁部分，随着运行时间不断延长，不锈钢与铸铁件部分的接触面逐渐因气蚀而脱离，空鼓的不锈钢与叶轮碰擦产生裂缝.经查其余6台机组叶轮外壳镶嵌不锈钢下方均出现大量气蚀坑，暂未出现不锈钢空鼓碰擦现象.

图1 叶轮外壳内嵌不锈钢裂缝Fig.1 Cracks of stainless steel embedded in impeller shell

叶轮外壳镶嵌不锈钢开裂的处理采取返厂进行受损部件重新镶嵌的方式进行解决.针对所有机组出现了铸铁件气蚀的故障，通过对气蚀面进行清理后，采取环氧树脂粘接填补，再进行磨平处理的工艺流程进行修复.

1.2 受油器发热抱死故障与分析处理

2019年7号主机拉杆上方受油器浮动瓦与调节杆抱死，严重发热烧损，叶片失去角度调节功能，操作油管受损面如图2所示.停机后检查发现叶轮密封老化导致漏油，渗漏部位如图3所示.受油器在运行中由于调节杆与浮动瓦一直处于相对运动中，当油供给不及时，导致调节杆与浮动瓦之间缺少油进行润滑，铜制的浮动瓦受热膨胀，进一步抱死调节杆，以致烧损失去调节功能.对7号主机受油器烧损部件进行更换，叶轮密封漏油则返厂更换密封件.通过维修的方式可以延长叶片调节机构的使用时间，但并未解决故障多发的根源问题.

2 轴流泵可靠性分析

针对四站叶轮外壳气蚀、调节杆抱死、叶轮密封漏油等故障的发生，本文在进行维修的基础上需要进一步对系统的可靠性进行安全判定，排查出故障隐患部位并进行维修乃至改造.本文采用计算流体动力学(computational fluid dynamic，CFD)技术分析四站立式轴流泵的力学性态，研究其可靠性.

图2 操作油管受损面Fig.2 Damaged surface of operation oil pipe

图3 叶轮密封渗漏部位Fig.3 Leakage part of impeller seal

CFD技术是目前解决三维流动问题的重要方法，该技术通过数学方程描述物理现象，采用相对简单的代数方程组实现数值模拟计算，以求得复杂流体流动的近似值[14-18].CFD数值模拟技术主要运用流体力学基本控制方程，包括连续性方程、能量/动量守恒方程.

对于湍流模型，本文选用标准k-ε湍流模型(standardk-ε)，并采用SIMPLE算法实现流体速度和压力的代数修正.由于湍流模型一般为高Re数模型，适用于离开壁面一定距离的湍流区域，对于高Re数模型区域，分子粘性系数μ很小，可忽略不计.对于靠近壁面的粘性底层，Re数很低，有必要考虑分子粘性的影响.

一般情况下，低雷诺数湍流模型和壁面函数是计算靠近壁面区域建模的有效方法.其中，低雷诺数模型较为复杂，需要在粘性底层中布置较多的节点；而壁面函数法可以将与壁面相邻的第一个节点布置在旺盛湍流区.使用壁面函数法可以有效降低计算消耗，但是该方法对于受粘性力影响的区域，如粘性底层及过渡区等是无法解决的.因此，壁面函数法对于壁面附近区域的流动更为适宜，该方法可以有效地确定扩散系数和k、ε边界条件，其主要步骤如下：

1) 假设在壁面附近粘性底层以外的区域，无量纲速度分布服从对数分布律，其表达式为

(1)

(2)

(3)

式中，k为湍动能.

2) 在划分网格时，把第一个内节点P布置到对数分布律成立的范围内，即配置到旺盛湍流区域.

3) 一个内节点与壁面之间区域的涡粘性系数μt按下式确定，即

(4)

式中，uW为壁面上的速度.因此可导出第一个内节点上μt的计算式.在第一个内节点上与壁面相平行的流速满足对数分布律，即

(5)

式中，E为与表面粗糙度有关的常数，E=9.8.

将式(4)、(5)相结合，得到节点P与壁面间的湍流粘性系数为

(6)

式中，μ为分子粘性系数.可以看出，上述算法成功的关键在于准确确定壁面上的涡粘性系数μt.

4) 对第一个节点P上kP和εP的确定方法做出选择.kP值仍可按k方程计算，其边界条件取为∂k/∂y=0(y为垂直于壁面的坐标).P点的ε值可通过代数方程求解，本文采用按混合长度理论计算，即

(7)

3 故障排查与解决

通过轴流泵内部流动模拟分析、叶片强度计算、调节机构受力分析、叶片调节机构故障分析等方面逐步排查立式轴流泵的故障隐患.

3.1 轴流泵内部流动模拟分析

3.1.1 计算模型

本文以轴流泵装置为分析对象，数值计算区域如图4所示，其中包含进水流道、叶轮(4个叶片)、导叶部分(7个导叶片)和出水流道.为了计算轴流泵装置内部的流动，将整个流动区域划分为转子区域和定子区域.考虑到转子区域附近的流动规律复杂，为有效模拟流场变化，在进行网格剖分时，将转子所处区域剖分得较密集一些，而流动相对稳定的定子区域则剖分得较稀疏，以构建合理的网格剖分区域，最后剖分得到的网格如图5所示.

图4 计算区域示意图Fig.4 Schematic diagram of calculation area

图5 轴流泵装置三维有限元网格Fig.5 Three dimensional finite element mesh of axial flow pump device

3.1.2 边界条件

2) 出口边界条件.对于不可压流动，假设出口边界条件满足充分发展，且边界参数对上游无影响.出口的各项参数则可外推求解，且各参数沿流线方向梯度为0，即

(8)

式中：φ为湍动能函数方程；n为垂直于壁面的局部坐标.

3) 周期性条件.假设转轮流道的进口和出口延伸段满足周期性边界条件，即

φleft=φright

(9)

式中，φleft和φright分别为单周期流域进口与出口左右侧节点内的通量变量值.

4) 固壁条件.对于固体边壁，本文采用粘性流体无滑移条件，脉动速度为0，时均速度也为0，ε设定为较小的有限值.

3.1.3 三维湍流流场模拟分析

基于江都四站轴流泵实际运行情况和前期设计资料的分析，对轴流泵在不同叶片角度、不同流量的工况下进行三维湍流流场分析.在分析过程中，坐标原点取在叶轮中心，始终以轴流泵装置出口处的静压力为参考压力，其值为0.

根据实际工作要求，本文研究分析三种工况，三种工况的叶片角度分别为4°、-2°和-6°，对应的泵送流量Q分别为42、35和31 m3/s，泵转速n均为150 r/min.按照上述模拟方法，可计算得到三种工况下的流线分布和静压分布，如图6～8所示.图中显示的压力为对应位置的相对压力，计算得到的叶轮和导叶表面静压分布可为下一步轴流泵受力特性分析提供技术支撑.

3.2 轴流泵叶片强度计算分析

采用三维空间有限元模拟技术对轴流泵叶片进行强度计算分析，假定叶片为线性定常系统，且为线弹性体，其实体建模如图9所示.在对模型进行网格剖分时，叶片选用十节点线性应变四面体单元剖分，可得叶片网格剖分模型如图10所示，共有节点27 980个，单元总数为15 477.叶片所受荷载包括自重、水压力和叶片旋转产生的离心力等，其中自重和离心力作用在整个叶片结构上.叶片枢轴和轮毂采用刚性连接，即在叶片枢轴与轴套接触面上节点的6个自由度均设为0.在进行强度校核时，采用第四强度理论的Von Mises Stress进行校核.

由此可计算得到三种工况下的叶片应力和应变，如图11～13所示.可以看出，叶片最大变形在轮缘的进水和出水侧处，应力集中在叶片根部，应力最大值分别为36.52、24.79和20.60 MPa.叶片材料为ZG0Cr13Ni4Mo，材料水中疲劳极限σ为171 MPa，因此，叶片最大应力远小于材料的水中疲劳极限，实际运行工况下叶片均在安全极限下运行.

3.3 轴流泵调节机构受力分析

图14为轴流泵调节机构工作受力示意图.由图14可以看出，轴流泵的拉杆受力主要包含自重和叶片表面上的压力，因此，叶片表面的受力分析就显得尤为重要.可调节叶片会受到水压力、离心力及机械摩擦力等外力所组成的力矩作用，调节机构必须克服这些力矩才能改变叶片安装角度，从而适应工况变化.

图6 叶片角度为4°，流量为42 m3/s时的流场速度和静压分布

图7 叶片角度为-2°，流量为35 m3/s时的流场速度和静压分布

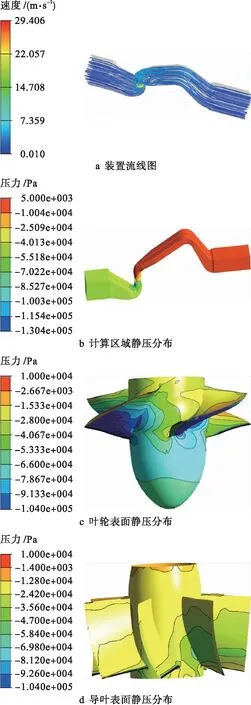
图8 叶片角度为-6°，流量为31 m3/s时的流场速度和静压分布

对于轴流泵叶片所受的水力矩，可通过对轴流泵装置的流场分析得到，三种工况下的叶片水力矩Mh分别为11 341、3 083和-3 624 N·m.叶片的离心力矩由于离心力方向与叶片转动枢轴不共面，由此形成对叶片转轴的作用力.旋转角速度、叶片几何尺寸及叶片安放角等是影响该力矩的主要因素.据此可计算得到叶片转角为+4°、-2°、-6°时的叶片离心力矩Mc分别为8 332.09、7 706.03和6 669.23 N·m，离心力矩随着叶片角度增大而增大，并且叶片离心力矩表现出叶片向关闭方向旋转的趋势.

图9 叶片实体Fig.9 Blade entity

图10 叶片计算区域网格图Fig.10 Meshing of blade calculation area

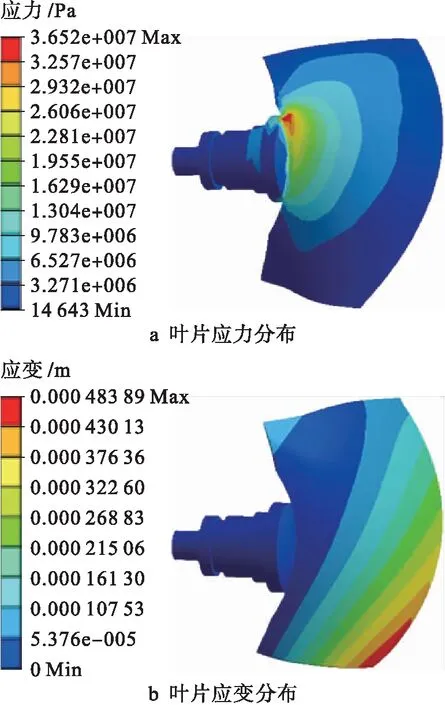
图11 叶片角度为4°，流量为42 m3/s时的叶片应力和应变分布图

图12 叶片角度为-2°，流量为35 m3/s时的叶片应力和应变分布图

图13 叶片角度为-6°，流量为31 m3/s时的叶片应力和应变分布图

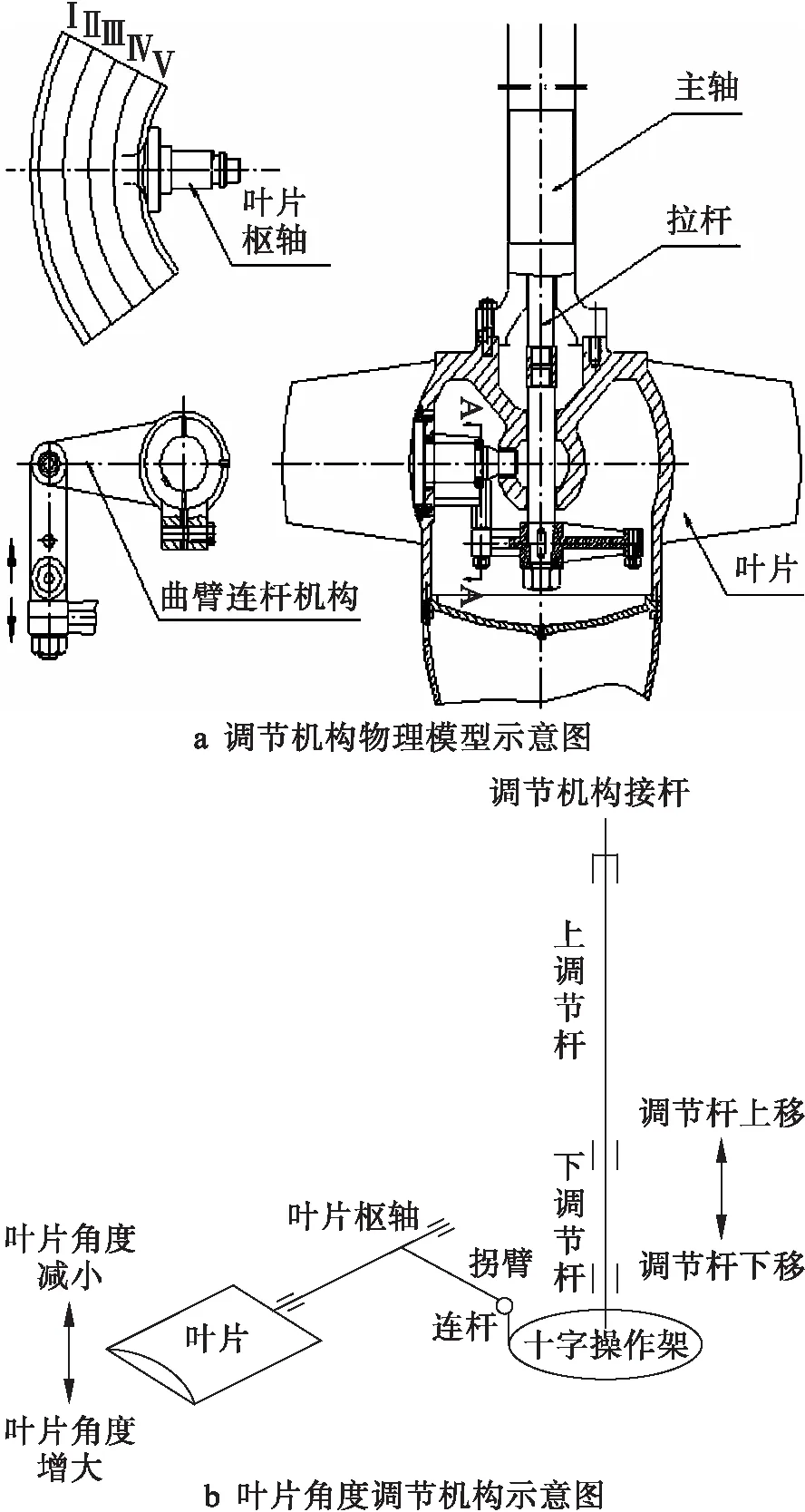
图14 轴流泵调节机构工作受力示意图Fig.14 Schematic diagram of working force of regulating mechanism in axial flow pump

叶片所受的摩擦力矩主要由叶片与轴套、叶片与卡环之间的摩擦力产生，而摩擦阻力大小受叶片受力状态影响，准确分析叶片受力才能得到较合理的摩擦力，由此分析得到的叶片与轴套以及叶片与卡环之间的作用力，用以准确计算叶片转动时需要克服的正压力，即得到叶片上的摩擦力，进而得到叶片调节需要克服的摩擦阻力.由此可计算得到三种工况下的叶片摩擦力矩分别为1 540、1 448和1 457 N·m.

Qqlq=±(Mh+Mc)+Mt

(10)

式中：Qq为转臂上的驱动力；lq为转臂长；Mh为叶片水力矩；Mc为叶片离心力矩；Mt为摩擦力矩.在计算时，驱动力Qq对叶片产生的驱动力矩为Mp=Qqlq，主要用于克服Mh、Mc和Mt.当调节杆下移时，叶片角度减小，式(10)则可取正号；反之，取负号.

图15为曲臂连杆机构的受力示意图，该机构是轴流泵的主要调节结构.图15中，φ为叶片转臂与水平位置的夹角，并规定自水平线开始算起，顺时针为正；垂直于连杆位置的偏转角为β.

图15 连杆机构受力示意图Fig.15 Schematic diagram of force of linkage mechanism

设连杆长为l，叶片在调节过程中，则有

lqcosφ+lsinβ=lq

(11)

若不计连杆的两个铰链的摩擦损失，则整个轴流泵的拉杆调节力可表示为

(12)

式中，Z为叶片个数.

据此可计算三种工况下叶片调节所需的调节力，当拉杆上移时，式(10)中取负号，三种工况对应的拉杆调节力分别为-16.79、69.39和134.29 kN；当拉杆下移时，式(10)中取正号，三种工况对应的拉杆调节力分别为51.98、-36.28和-101.06 kN.拉杆调节力均在最大允许调节力300 kN的安全范围内.

3.4 叶片调节机构故障分析与改造

通过以上计算可知，轴流泵的叶片强度、曲臂连杆机构受力均在安全范围内，运行稳定可靠.系统故障多发于叶片调节机构的渗漏油、受油器发热抱死等，其根本原因在于叶片调节机构油路控制部分的复杂结构：1)采用外供油系统，多台主机的叶片调节机构共用一套液压站，导致管路接头多，渗漏隐患点多，当局部渗漏量过大时影响相关机组叶片调节；2)受油器的机械机构导致浮动瓦与调节杆之间一直处于相对移动摩擦的状态，一旦液压油润滑不到位就会导致金属结构因摩擦大量发热，进而膨胀抱死，导致叶片调节失灵.图16为原油压调节机构系统图.

针对以上问题，江都四站开展了内置式叶片调节机构改造，很好地解决外置式叶片调节机构的问题，如图17所示.1)将微型液压站内置于油缸内，解决了外置式液压站管路接头多、渗漏点多的隐患；2)上置式的油缸、调节杆与大轴、叶片同步旋转，解决了原受油器基座不转，浮动瓦和调节杆转动导致的发热问题；3)每台机组单独一套液压站系统，各台机组之间相互独立，单台机组叶片调节机构故障不影响其他机组.1号主机组叶片调节机构更新改造后于2020年投入运行，累计运行1 451.4台时，未发生渗漏油现象.

4 结 论

江都四站针对运行中发生的叶轮外壳镶嵌不锈钢开裂、铸铁部分严重气蚀、叶片调节机构抱死、叶轮密封老化漏油等故障进行维修处理的基础上，进一步对轴流泵力学性态展开了研究分析，通过流体动力学对三种叶片角度下的轴流泵内部湍流状况进行了模拟，重点分析了轴流泵的流场速度和静压分布.在此分析结果基础上，采用三维空间有限元技术，对轴流泵叶片展开数值模拟和受力分析，并对叶片强度展开了校核，结果显示叶片最大应力均远小于叶片材料的水中疲劳极限.最后对轴流泵调节结构展开了受力分析，由此计算了各工况下拉杆上移和下移时的调节力，计算结果显示拉杆调节力均在安全允许范围内.通过逐步排查最终确定了液压站外置和系统油路复杂是渗漏油故障多发的根源.在对故障机组进行维修的基础上，通过每年一台机组进行内置式叶片调节机构改造，逐步消除渗漏油等隐患.

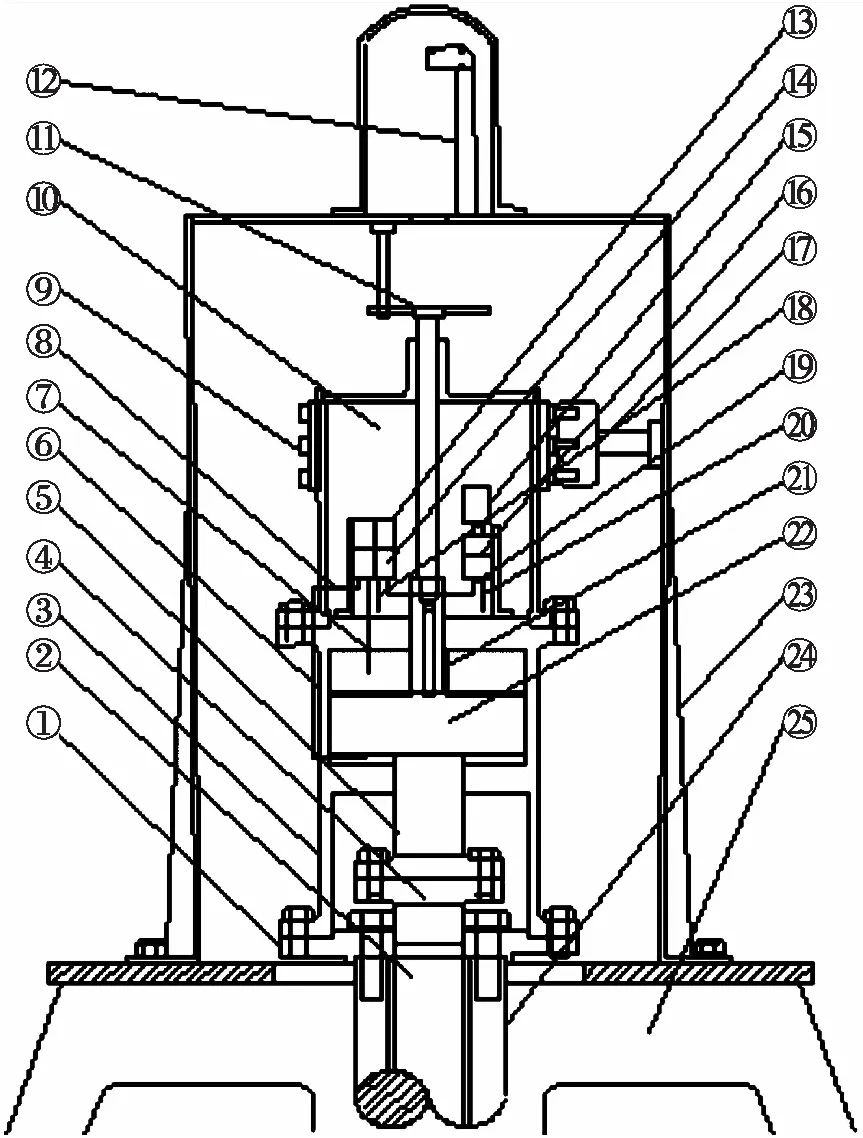
①连接底板 ②调节杆 ③底座 ④联轴器 ⑤活塞杆⑥油缸 ⑦下高压油管 ⑧上高压油管 ⑨集电环 ⑩储油箱 角度传感器 激光传感器 电磁换向阀 液控单向阀 电机 液压站 碳刷 回油管 高压油管 进油管 导向轴 活塞 外罩 转子主轴 主电机上盖