基于MMSE准则的5G正交时频空信号检测算法

赵 巍

(华东交通大学 理工学院， 南昌 330100)

随着无线通信技术的迅速发展，具有更高效率和更低时延等多种优点的多输入、多输出技术(MIMO)逐渐成为第5代移动通信系统(5G)的关键技术.空间调制技术通过融合纠错编码和星座调制，利用激活天线索引的方法，实现了比特信息的调制与解调.该技术基本避免了空间复用和空间分集的诸多缺点，同时提高了信号传输的可靠性与安全性，所以吸引了众多研究者的关注.Garcia等[1]提出了基于压缩感知的信号检测算法，为多用户的5G多址通信信号传输算法提供了更多的选择；Jeganahan等[2]利用经典ML检测算法，实现了用户天线组合和星座符号的搜索；Renzo等[3]利用最小均方误差准则，提出了基于多种算法的信号检测方案，大幅度地降低了计算过程的复杂度.此外，国内的多位学者也曾经提出很多值得借鉴的算法[4-9]，然而这些算法均未能完全避免当前5G通用信号检测算法的主要缺点[10-15].针对这一研究现状，本文通过融合空间调制和正交时频空技术构建广义的空间调制正交时频空系统，解决由高速移动带来的信号频率偏移等问题.同时在传统频域均衡算法的基础上，利用最小均方误差(MMSE)准则提出了具有更低计算复杂度和更高检测性能的判决反馈检测算法.此外，利用Matlab软件对该检测算法进行了仿真分析，与传统的频域均衡算法相比，所提算法具有更加优秀的系统性能和更低的计算复杂度.

1 广义空间调制正交时频空系统

针对高速通信信号存在的多普勒效应，文中将融合空间调制技术和正交时频空技术结合，提出具有较大参考价值与推广意义的空间调制正交时频空系统.在广义空间调制正交时频空系统中，信号发送方通过辛有限傅里叶逆变换(ISFFT)和傅里叶逆变换(IFFT)分别实现了频域和时域原始信号的调制，并通过相应的信道传送到信号接收端，分别实现了时域和频域的调制信号解调过程，从而完成系统的信号传输.

在正交时频空系统中，设信号发射方天线数为ne，接收方天线数为nr，发射天线激活个数为na，系统包含T个子载波和L个时隙.此时，正常工作的激活发射天线组合种类个数为

(1)

根据信息理论，为了用符号Ii(1≤i≤B)表示某种激活发射天线组合，文中需要使用log2B个比特信息.另外，令S表示星座信号的阶数，为了实现对na个星座信号的调制，本文需要nalog2S个信号比特.令l∈[1，L]且t∈[1，T]，则在第l个时隙中，第t个子载波表示为

m(l，t)=[0，…，0，si1，0，…，0，si2，0，…，0，sina，0，…]

(2)

此时，第i个信号发射天线在所有时隙中子载波矩阵为

(3)

在信号发射方，利用辛有限傅里叶逆变换和傅里叶逆变换即可实现通信信号的调制[7-8]，其信号转换表达式为

Gi(l，t)=ISFFT(mi(l，t))=

(4)

(5)

式中，b和c为中间计算变量.第l个时隙第t个载波天线接收信号为

(6)

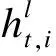
令Xi(n)和Yt(l)分别表示接收信号的时域和频域信号，Z(l)表示信道噪声的频域信号，则傅里叶变换和辛有限傅里叶变换的计算过程可表示为

(7)

对频域信号Yt(l)进行辛有限傅里叶变换，则天线接收信号表示为

yi(l，t)=SFFT(Yt(l))=

(8)

式中，χ和δ为计算中间变量.由式(8)可以进一步得到天线的接收信号矩阵Y.

2 信号检测算法

为了进一步提高接收信号的抗干扰能力[9-11]，文中提出了一种基于MMSE准则的低复杂度信号检测算法.

2.1 基本框架

为了提高信号检测抗干扰能力，同时降低算法的计算复杂度，文中在信号接收端设置前向频域滤波器和反馈时域滤波器[12].同时结合快速傅里叶变换和辛有限傅里叶变换，从而实现信号的判决、反馈和检测等多种功能，基本计算框架如图1所示.

2.2 算法原理

令F和W表示前向频域均衡滤波器和反馈时域均衡滤波器，则这两个滤波器在第i根发射天线、第l个时隙和第t个载波上的响应表达式为

(9)

(10)

令P表示临时计算参数，则转换后的时域信号xi(l，t)可表示为

图1 基于MMSE准则的信号检测算法计算框架Fig.1 Calculation framework of signal detection algorithm based on MMSE criterion

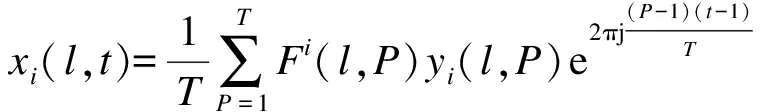
(11)

在获取时域信号后，算法使用反馈时域均衡滤波器W消除时域信号xi(l，t)中包含的符号内和符号间等多径干扰.令vi(l，t)表示去除多径干扰的时域判决信号，其计算表达式为

vi(l，t)=xi(l，t)-∑W(i，l)(s)V(l，t-s)

(12)

式中，V(l，t)为时域计算过程的判决信号.

利用均衡滤波器获取第l个时隙第t个载波的频域发射信号，使用辛有限傅里叶变换可以将其转换为多普勒域的时域信号xi(d，k)，令d∈[1，L]，k∈[1，T]，其计算表达式为

(13)

通过对多普勒域信号xi(d，k)进行辛有限傅里叶逆变换和傅里叶逆变换，从而获取最终的时域接收信号φi(d，k).

2.3 滤波系数

基于MMSE准则[14-15]，文中提出了具有较低计算复杂度和较高抗干扰性能的信号检测算法.在该算法中，前向频域均衡滤波器F和反馈时域均衡滤波器W具有较为关键的作用，其具体性能表现和系数推导质量之间的关系尤为密切.针对该问题，本文提出了相应的推导方法.

对于时域估计信号φi(d，k)，令Φ(d，k)为其矩阵表示，γ为滤波器函数的自变量，则xi(d，k)实际误差可表示为

φi(d，k)

(14)

时域估计信号的均方误差计算表达式为

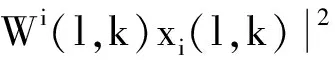
(15)

式中：Fi(l，k)与Wi(l，k)分别为前向滤波器和反馈滤波器的频域响应函数；xi(l，k)与yi(l，k)分别为第l个时隙第k个载波的频域发送信号和频域接收信号.

3 算法分析与仿真

为了充分衡量基于MMSE准则的信号检测算法，首先，本文对该算法进行了计算复杂性分析，其次，利用MATLAB软件实现了经典球形译码和基于MMSE准则的信号检测算法的对比分析.其中，球形译码是通信系统中常用的经典信号检测和译码算法，其基本原理是利用最大似然译码原理搜索设定有限球形区域，从而实现通信接收信号的检测.

3.1 计算复杂度分析

针对经典球形译码算法和基于MMSE准则的信号检测算法，本文做出了详细的计算复杂度分析.基于MMSE准则的信号检测算法计算复杂度可表示为

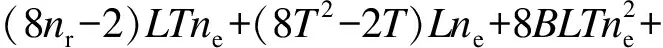
(8T2L-4LT+8TL2)ne+(8T2L-4LT+

8TL2)ne+(8nr-2)TLne+(8T2-2T)Lne+

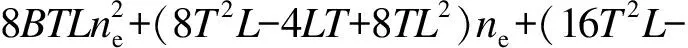
6TL+8TL2)ne+(8Bne-2ne+2)LTne+

(16)

通过分析经典球形译码的详细计算过程，获取了其复杂度的计算表达式为

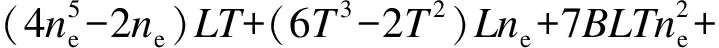
(4T2L-4LT+3TL2)ne+(5T2L+4TL2)ne+

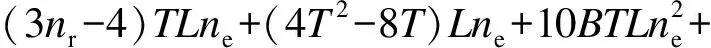
(6T2L-7LT+8TL2)ne+(15T2L-6TL+

8TL2)ne

(17)

3.2 仿真分析

本文利用Matlab软件分别对球形译码算法和文中提出的算法进行了仿真分析.球形译码算法具有适中的计算复杂度和优秀的信号检测性能.通过对比球形译码算法，可以充分评估基于MMSE准则的信号检测算法.

在系统中，设置信号的载波频率f=4×109Hz，采样周期D=1/15 000，系统采用QPSK的方式进行调制，分别通过4组和8组发射、接收天线.文中对球形译码和MMSE准则检测算法在信噪比(SNR)为-15～15 dB情况下的误比特率(BER)进行了仿真，仿真结果如图2、3所示.

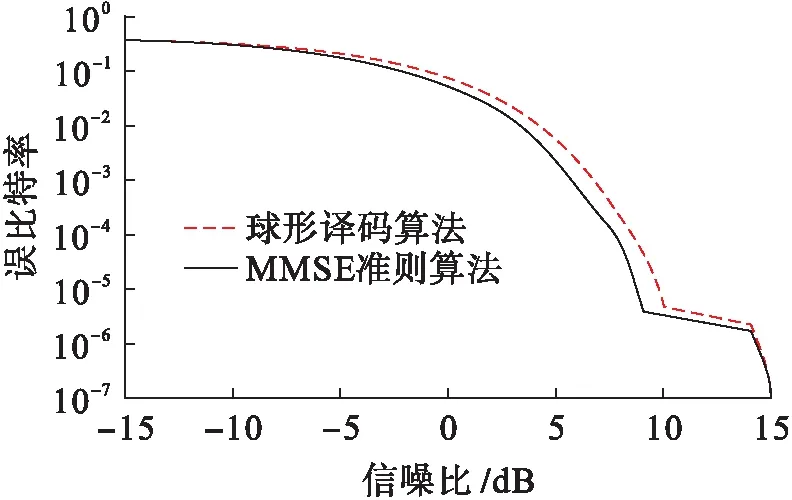
图2 4组发射和接收天线时两种算法的误比特率对比Fig.2 Bit error rate comparison for two algorithms with 4 sets of transmitting and receiving antennas

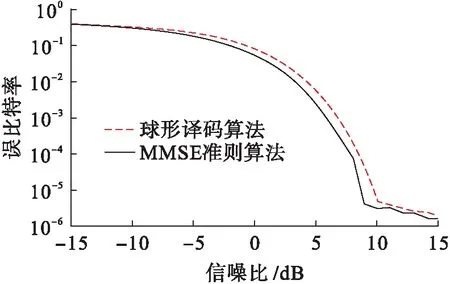
图3 8组发射和接收天线时两种算法的误比特率对比Fig.3 Bit error rate comparison for two algorithms with 8 sets of transmitting and receiving antennas

根据图2可知，两种算法的误比特率初始时处于较高的水平，然后迅速降低；在信噪比达到10 dB时，两种算法的误比特率进入相对稳定的状态；到达14 dB时，误比特率继续急剧下降，直至可以忽略不计.这样的误比特率总体符合算法的设计预期，但当信噪比达到14 dB时，误比特率呈现出不稳定的趋势.根据图3可知，在到达10 dB时，两种算法的误比特率下降速度降低，并趋于相对稳定，直至忽略不计.当信号信噪比处于-15～10 dB时，两种算法误比特率随信噪比的增加而迅速下降；当信号信噪比处于10～15 dB时，两种算法误比特率随信噪比的增加而降低，但其速度趋于稳定；当信号信噪比大于14 dB时，两种算法误比特率处于较低的水平，误比特率基本可以忽略不计.

根据图2、3的仿真结果可知，基于MMSE准则的信号检测算法误比特率始终低于球形译码算法，算法可以有效提升通信系统的信号检测功能，降低通信系统中的多径干扰，优于传统的球形译码算法.

4 结 论

基于MMSE准则，文中提出了适用于5G通信系统的信号检测算法.该算法主要应用于广义的空间调制正交时频空系统，具有较高的抗多径干扰能力，能够有效地提高通信系统的性能.然而由于计算资源和外界条件的限制，本文未能在户外环境进行广泛的实验，导致文中算法仍可能存在未知的缺陷和不足，在下一步的研究工作中，将致力于该算法的进一步优化和应用.